网格锚定单体碟形网箱的水动力特性研究
徐为兵, 朱克强, 张大朋, 杨然哲
(宁波大学 海运学院, 浙江 宁波 315211)
过度捕捞和近海海洋环境污染导致近岸海洋渔业资源枯竭。发展创新型渔业, 大力调整渔业产业结构, 转变渔业经济的增长方式是我国渔业的政策导向。深水抗风浪网箱是全球沿海国家开发海洋经济的重要战略装备, 也是我国新时期现代农业向海洋领域拓展的重要战略需要。我国深水网箱养殖事业起步比较晚, 与挪威、美国、日本等国在深水养殖领域存在相当差距。目前综合各方面因素来看, 结构形式较为简单、管理较为方便而且价格较低廉的重力式网箱更适合我国的国情, 全国绝大多数采用的都是此类网箱。张雅芝[1-2]等从水产养殖的角度分析了我国海水网箱养殖长久以来存在的各种问题, 如网箱的布局、管理和鱼类病害等, 这些问题制约着我国网箱养殖的发展。但是如果能在认识这些问题的基础上, 加强对海水养殖容量的研究, 开发优良品种,保护种质资源并加强养殖水环境保护和病虫防护,就能实现网箱养殖的可持续健康发展; 徐君义等[3]根据实际试验海区网箱养殖的成果, 针对网箱的材料、鱼种的选择与运输, 总结出了实际养殖过程中发现的一些经验; 王福表[4-5]则专门分析了网箱养殖水域污染源的成因和特点, 并根据实际考察给出了水污染治理的一些相关对策。同时, 作者针对网箱的有机质淤积带来的危害, 研制了一种在沉降物未到达水底前就能被收集清除的新型网箱。虽然目前浮式重力式网箱应用较广, 但它在强水流作用下, 网衣水平漂移严重, 网箱容积损失率高, 而加载保持网型的同时, 会使网衣承受的张力增加, 容易造成网衣撕破。因此, 在流速较大海域中, 该网箱的使用受到限制[6]。可见, 对先进网箱的了解和研究是必不可少的, 比较典型的为美国式钢质升降式大型深水网箱, 国内也称之为飞碟型可潜式大型深水网箱。国内外有关圆形重力式网箱数值模拟和模型实验的研究成果比较丰富, 而目前为止国内对于碟形网箱只有较为详尽的结构介绍和初步的水动力估算[6-10], 孙满昌等[11], 李玉成等[12-13]对碟形网箱也仅仅是进行了模型实验方面的研究。本文基于凝集参数法, 运用 OrcaFlex建立碟形网箱模型,通过数值模拟研究波流联合作用下碟形网箱的缆绳受力特性和网箱结构的运动响应, 以期深入了解碟形网箱的水动力特性, 为碟形网箱及其锚泊系统的研究提供参考。
1 数值模型
本文研究的对象为沉降式碟形网箱。该网箱为一个自张紧结构, 主要由一个八边形浮环和一个中心立柱组成。网箱浮环由8个钢管分段用法兰连接,每个分段分别密封并加压。立柱和浮环的材料均为镀锌钢, 用16根辐绳连接。中心立柱直径为0.92 m,长9.14 m, 浮环的公称直径为15 m, 单根浮环管径为27.3 mm, 辐绳材质为聚乙烯, 直径13 mm。网箱用重达3 t的混凝土块压载, 通过悬挂索悬挂在中心立柱下面, 使之保证一定的稳性。中心立柱内有一个长达 3 m的体积可变的浮舱, 配合一定长度的悬挂索能使网箱下潜到特定的深度。网箱及锚泊系统的具体尺寸及浮标与网箱连接细节见参考文献[14-15]。本文利用基于凝集参数法的专业水动力分析软件OrcaFlex建立真实的网箱模型, 如图1所示。有关凝集质量法的理论可见朱克强等[16-18]的研究, 在此不再详细介绍。由于本文研究的主要内容是网箱整体和锚泊系统的水动力响应, 因此对网箱各种构件之间复杂的连接作了必要的简化, 如绳索之间的连接全部简化为铰接。同时为了节省计算时间, 本文没有真实模拟网衣受力, 并选用工程上常用的 Airy波理论和均匀流进行各种组合来对网箱养殖系统施加不同的环境载荷, 通过时域模拟后得到了不同载荷下的网箱水动力结果, 结合水动力分析结果给出了深海网箱在布锚过程中应注意的事项, 对实际工程实践有一定的指导作用。
建模主要的思想是将整个网箱结构分割成受外力作用的若干个单元, 然后将外力平均分配到每个对应的节点, 形成一系列的运动方程。为了初步规划和设计, 我们应用修改后的 Morison方程(公式(1)),来计算作用在笼状结构小部件上的波浪力。

其中,m表示水质点的质量,ρ是海水的密度,Km是附加质量系数,CD是曳力系数,CM是惯性系数,A是投影面积, ∀是网箱系统小部件排开水的体积,并且VR=V-R˙, 是水粒子速度V相对于结构速度R˙。公式(1)右边的第一项通常认为是曳力, 而第二项称为惯性力。所有的这些力是由一个受到海洋环境负载的移动物体激发的。不过, 当处理一个特定的单元时, 其他外部力, 如浮力、物重、和锚绳或网线伸长时产生的张力, 计算时都应包括在内。因此, 由牛顿第二定律可得, 公式(1)可以表示为:

其中FD是阻力,FI的惯性力,FB浮力,FW是重力,FT是张力。
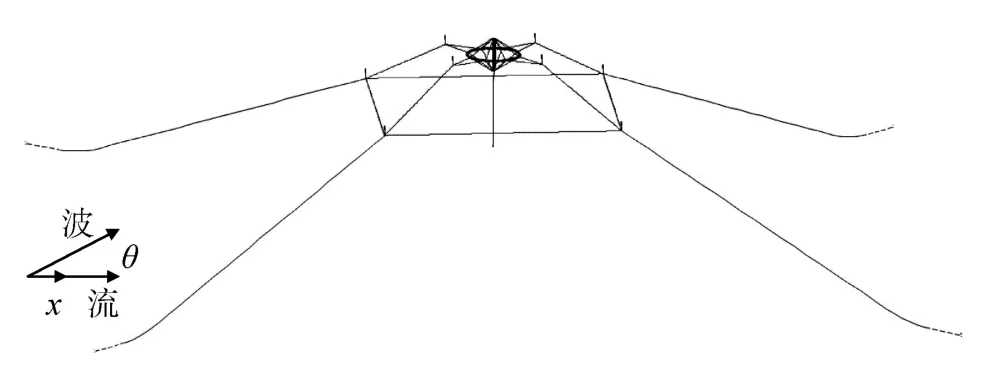
图1 网箱模型示意图Fig. 1 The model of the sea station
本文在建模过程中做了相应的处理, 如网箱中作为加强筋的辐绳之间并没有网衣, 因此网箱整体受到的水动力有所减少, 但本文探究的是网箱系统整体的运动规律, 对网衣细节的模拟有待后续进一步的研究。八边形浮环之间通过6D浮标相连, 为了确保浮环作为一个整体参与水动力计算, 浮环之间的端部的强度设为无限大。浮标在此只是起到连接作用, 并不参与水动力计算。软件中对细长型结构均采用凝集质量模型, 该方法不仅计算速度快, 还具有较高的计算精度, 已经得到广泛认可, 因此本文网箱系统模型中计算得到的锚泊张力具有一定的合理性。
2 算例分析
在深海区域, 常常会遇到台风等恶劣天气, 波浪和海流会同时出现, 锚泊系统将限制网箱的运动,保证网箱结构和鱼群的安全。在波流联合作用下, 网箱锚绳的受力将在一定程度上反映网箱整体结构的受力。一旦锚泊系统失效, 不仅会造成鱼群逃逸和死亡, 还会对网箱结构造成严重破坏, 给养殖者带来巨大的经济损失, 因此研究锚泊系统的安全性是很有必要的。
本文研究在水深为55 m的深海中, 各种波流组合对网箱系统的作用, 包括3个波高(2、4、6 m)和3个周期(6、9、12 s)以及 4 种流速(0~2 m/s)[19]。需要注意的是, 软件中默认的波流前进方向均为 180°(图中所示海流流向为0°)。图2显示的是在纯波作用下,迎流面锚绳上的最大张力与波浪周期和波高H之间的关系。由图可知, 周期相同时, 纯波作用下的锚绳张力均与波高大致呈线性关系; 波高一定时, 锚绳的张力随周期的变化并不明显, 且周期越大, 锚绳张力的几乎保持不变。
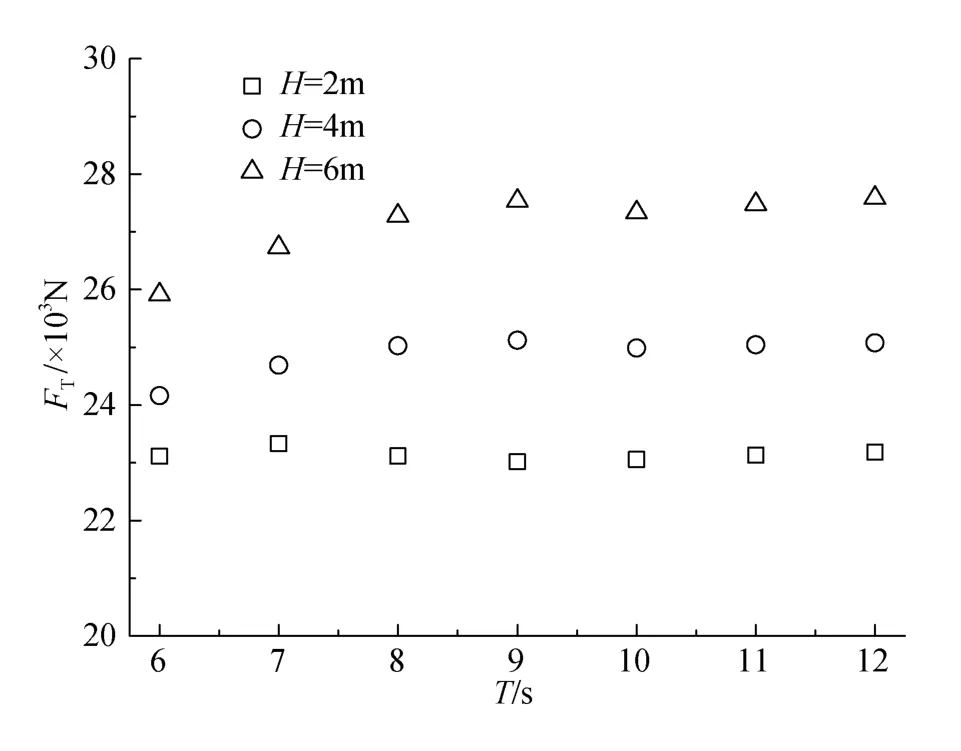
图2 锚绳张力随周期的变化Fig. 2 Changes of mooring line tension in various periods
图3显示了单个网箱系统在各种波流联合作用下时迎流面锚绳张力的最大值。由图3a~图3c可知,波浪周期较长, 流速相同时, 相同波高作用下的网箱锚绳张力的最大值几乎相同; 当波浪周期一定时(图 3d~图 3f), 波高越大, 网箱系统的锚绳张力最大值也越大; 且随着流速的均匀增加, 锚绳张力最大值并不是线性增加, 而是呈现出增幅越来越快的趋势。波浪周期越小, 流速越大, 水粒子的水平方向的合速度就越大, 由公式(1)可知, 网箱系统受到的水动力就越大, 波浪的波高越大, 水粒子的垂直方向上的速度就越大, 水动力也同样会增大。
综合对比以上各图可以发现, 在本文的研究中,波流参数对网箱锚绳最大张力影响的重要程度依次为: 流速V, 波高H, 周期T。
对于沉降式碟形网箱来说, 遇到台风等恶劣天气时迅速下沉到海底是保证网箱结构安全完整的重要手段。因此研究极限海况下网箱下沉时的受力情况也很有必要。深海中的波浪和海流前进的方向并不总是相同, 为了研究斜入射波和海流对锚绳张力的影响, 我们假设均匀流流只沿着x轴正方向运动,但波浪入射的角度不同。
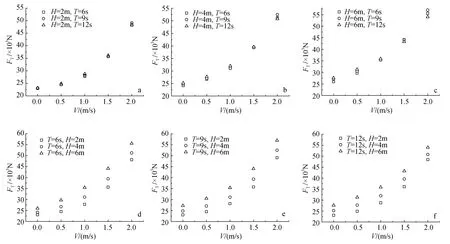
图3 碟形网箱系统在不同波流状态下的锚绳最大张力Fig. 3 The maximum mooring line tension induced by various wave-current conditions
图4是在均匀流速为1.5 m/s时, 迎流面锚绳最大张力与入射波(H=6 m,T=9 s)前进角度的关系。从图中可以看出, 锚绳的最大张力随着入射波角度的变化呈周期性变化; 波流同向时要比波流逆向时的锚绳张力要大, 但最大张力发生在波流夹角为 135°左右的情况下, 与前人研究的结果相符; 而且从图中可以看出, 网箱下沉能明显地减少锚绳的受力,在本例中网箱下沉能使锚绳受力减少35%~43%。当波流夹角为 135°时, 在波浪前进的方向上 1#缆绳承受网箱整体受到的波浪力最大, 因此表现为此时 1#缆绳上的锚泊张力最大。本例计算得到的结果可以指导养殖户在特定海洋环境下合理布置网箱的锚泊位置, 避免出现最大锚绳张力情况, 间接提高深海网箱系统的安全性, 减少不必要的损失。

图4 锚绳张力随入射波角度的变化Fig. 4 The maximum mooring line tension induced by various incident angles of waves
如图 5所示, 取浮环两侧中点 A、B, 假设浮环在波流联合作用下发生的转动和变形幅度很小, 则浮环整体的倾角可以通过A、B两点的连线与水平线之间的夹角θ来表示。本文计算了不同波流作用情况下网箱漂浮时的浮环最大倾角, 如图6所示。
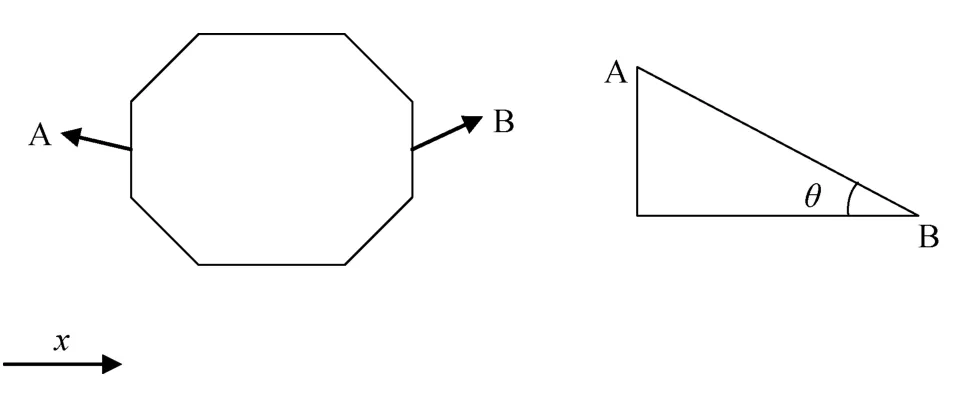
图5 浮环倾角计算示意图Fig. 5 The inclination calculation diagram of floating ring

图6 碟形网箱系统在不同波流状态下的浮环最大倾角Fig. 6 The maximum inclination induced by various wave-currents
由图 6a~图 6c可知, 波高一定时, 浮环的倾角与流速大致呈线性关系。周期较小时(6 s), 浮环倾角会明显较大; 相同流速下, 周期较大(9 s和12 s)、波高较小时(2 m和4 m)浮环倾角的差值很小, 但这个差值会随着流速的增加而逐渐变大。由图6d图6f可知, 周期一定时, 浮环倾角和流速呈线性关系, 随着波高的增加而增大, 但增大的幅度随着流速和周期的增加而减小。
3 结语
纯波作用下, 波浪周期相同时, 锚绳张力随波高线性增加; 波高一定时, 锚绳张力随周期的变化并不明显, 且随着周期越来越大, 锚绳张力趋于不变。
波流联合作用下, 波浪周期较长时, 锚绳的最大张力几乎相同; 当波浪周期一定时, 波高越大, 锚绳最大张力也越大, 且流速越大, 锚绳最大张力随波高增加的幅度越小。波流参数对网箱锚绳最大张力影响的重要程度依次为: 流速V、波高H、周期T。
海流方向一定时, 锚绳最大张力随波浪的入射角呈周期性变化; 波流同向要比波流逆向时的锚绳张力要大, 且波流夹角为 135°时, 迎流面锚绳张力最大; 网箱下沉能明显减小网箱运动幅度和锚绳受力。
各种工况下, 浮环倾角大小在 25°以内, 其值随流速线性增加, 随着波高的增加而增大, 但增大的幅度随着流速和周期的增加而减小。
[1] 张雅芝. 我国海水鱼类网箱养殖现状及其发展前景[J].海洋科学, 1995, 5: 21-24.
[2] 张雅芝, 苏永全. 论我国海水鱼类网箱养殖的可持续发展[J]. 海洋科学, 2001, 7: 52-56.
[3] 徐君义, 金伟良. 浅海抗风浪网箱养鱼技术研究[J].海洋科学, 2001, 1: 12-14.
[4] 王福表. 网箱养殖水污染及其治理对策[J]. 海洋科学, 2002, 7: 24-26.
[5] 王福表. 水产养殖清淤网箱的研制和应用[J]. 海洋科学, 2002, 7: 12-14.
[6] 袁军亭, 周应祺. 深水网箱的分类及性能[J]. 上海水产大学学报, 2006, 03: 3350-3358.
[7] 郭建平, 吴常文. 美国式钢质升降式大型深水网箱结构原理的研究探讨[J]. 渔业现代化, 2004, 1: 28-31.
[8] 章守宇, 刘洪生. 飞碟型网箱的水动力学数值计算法[J].水产学报, 2002, 6: 519-527.
[9] 夏泰淳, 张健. 深水双锥型网箱的阻力估算[J]. 上海水产大学学报, 2003, 1: 87-91.
[10] 刘健, 夏泰淳, 许柳雄. 深水双锥型网箱的水动力估算[J].浙江海洋学院学报(自然科学版), 2007, 3: 257-265.
[11] 孙满昌, 张健, 钱卫国.飞碟型网箱水动力模型试验与理论计算比较[J].上海水产大学学报, 2003, 4: 319-323.
[12] 李玉成, 宋芳, 董国海, 等. 碟形网箱水动力特性的研究[J].海洋工程, 2004, 4: 19-25.
[13] 李玉成, 桂福坤, 宋芳, 等. 重力式与碟形网箱的锚绳受力特性比较[J].海洋工程, 2005, 4: 19-24.
[14] Fredriksson D W, Muller E, Baldwin K, et al. Open ocean aquaculture engineering: system design and physical modeling[J]. Marine Technology Society Journal, 2000, 34(1): 41-52.
[15] Tsukrov I I, Ozbay M, Swift M R, et al. Open ocean aquaculture engineering: numerical modeling[J]. Marine Technology Society Journal, 2000, 34(1): 29-40.
[16] ZHU K Q, CAI Y, YU C L, et al. Nonlinear Hydrodynamic Response of Marine Cable-Body System Undergoing Random Dynamic Excitation[J]. Journal of Hydrodynamics. 2009, 21(6): 851-855.
[17] 朱克强, 郑道昌, 张玉松, 等. 随机波浪下遥控潜水器强非线性耦合空间运动与缆索安全性研究[J]. 海洋工程, 2010, 2: 95-99.
[18] 朱克强, 朱海洋, 于春令, 等. 深海遥控潜水器多体系统非线性耦合动力特性模拟[J]. 海洋工程, 2008, 1: 83-87.
[19] Huang C C, Tang H J, Liu J Y. Effects of waves and currents on gravity-type cages in the open sea[J].Aquacultural Engineering, 2008, 38(2): 105-116.

