区间线性系统的Farkas型定理

(杭州电子科技大学运筹与控制研究所，浙江 杭州310018)

0 引 言

著名的Farkas 定理及其各种推广形式一直被广泛地应用于线性优化和非线性优化问题。近年来，越来越多的学者注重区间线性优化的研究，因此将Farkas 定理推广到区间系统中是非常有必要的。从1989年Rohn[1]首次将Farkas 定理推广到区间线性方程组的弱可行开始，直至目前，区间线性系统(包括区间线性方程组和区间线性不等式组)的8个问题的Farkas型充要条件都已被建立[2-4]。最近，Li等[5]提出了关于区间线性系统新的统一的模式，如何将Farkas 定理推广到这个新的区间线性系统是本文将要探讨的问题。

1 若干定义和引理

记{±1}m为各分量都是{1，-1}的m-维向量的全体，令e= (1，1，…，1)T是各分量都为1的m-维向量，一个矩阵A= a()ij的绝对值是指故可得对于一个给定的向量y∈Rm，记Ty=diag(y1，y2，…，ym)为相应的对角矩阵。对每一个x∈Rn，记它的符号向量为sgn x，定义为:这里i=1，2，…，n。因此得到这里z=sgn x∈{±1}n。给定一个区间矩阵AΙ=[Ac-AΔ，Ac+AΔ]，对于任意的向量y ∈Rm和z∈Rn，定义矩阵:Ayz=Ac-TyAΔTz。类似的，对于一个区间向量bΙ=[bc-bΔ，bc+bΔ]以及任意向量y∈{±1}m，定义向量:by=bc

设ΙRm×n是一个m×n的区间矩阵，IRm是一个m-维的区间向量，令AΙ∈IRm×n，bΙ∈IRm。一个区间线性系统如下:

它表示下列线性方程的集合:

其中，A和b 满足:

如果存在A和b 满足条件式(3)并且使式(2)是可解的(或可行的，即式(2)有一个非负解)，那么就称区间系统(1)是弱可解(或弱可行)。如果对任意满足条件式(3)的A和b 都能够使得式(2)是可解的(或可行的)，那么称区间系统(1)是强可解(或强可行)。用同样的方法可以定义出区间线性不等式组的弱可解(或弱可行)和强可解(或强可行)。

如果对任意的b∈bΙ都存在A∈AΙ使得式(2)可解(或可行)，那么就称区间线性系统(1)是 (bI)-强可解(或强可行)。类似地，可以定义出区间线性不等式组AΙx≤bΙ的(bI)-强可解(或强可行)[5]。

下面几个关于区间线性系统弱可解和弱可行的Farkas型定理被用来获得接下来一节中的主要结果[5]。

引理1系统AΙx=bΙ是弱可行的当且仅当 (∀p)(AΤp≥0，∀A∈AΙ⇒bΤp≥0，∃b∈bΙ)。

引理2系统AΙx≤bΙ是弱可行的当且仅当 (∀p≥0)(AΤp≥0，∀A∈AΙ⇒bTp≥0，∃b∈bΙ)。

引理3系统AΙx≤bΙ是弱可解的当且仅当(∃z∈{±1}n)(∀p≥0)((Aez)Τp=0⇒bΤp≥0，∃b∈bΙ)。

引理4系统AΙx≤bΙ是弱可解的当且仅当

2 主要结果

本节的主要目的是给出区间线性方程组的(bI)-强可行，以及区间线性不等式组的(bI)-强可解和(bI)-强可行的Farkas型充要条件。

定理1 区间线性系统AΙx=bΙ是 (bI)-强可行的当且仅当:

证明 必要性。令AΙx=bΙ是 (bI)-强可行的，因此对任意的b∈bΙ都存在A0∈AΙ使得方程A0x=b 有非负解。如果向量p 满足对任意的A∈AΙ都有ATp≥0，则表示A0Tp≥0。因此对任意的b∈bΙ都有bΤp= (A0x)Τp=xΤA0Τp≥0。

充分性。令式(4)成立。假设该区间系统AΙx =bΙ不是 (bI)-强可行的，则表示存在b0∈bΙ使得对任意的A ∈AI方程Ax=b0都没有非负解，即AΙx=b0不是弱可行的。所以由引理1 得(∃p)(AΤp≥0，∀A∈AΙ⇒b0Τp＜0)，该式等价于:

显然，式(5)与式(4)矛盾。因此，系统AΙx=bΙ是 (bI)-强可行的。

定理2 区间线性系统AΙx≤bΙ是 (bI)-强可行的当且仅当:

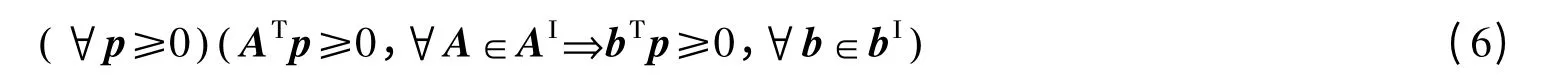
证明 必要性。令AΙx≤bΙ是 (bI)-强可行的，则对于任意的b∈bΙ都存在A0∈AΙ使得不等式A0x≤b 有非负解。如果向量p≥0 满足:对任意的A∈AΙ都有ATp≥0，则表示A0Tp≥0。因此，对任意的b∈bΙ有bΤp≥ (A0x)Τp=xΤA0Τp≥0。

充分性。类似于定理1 充分性的证明，采用反证法，再应用引理2 即可得证。

定理3 区间线性系统AΙx≤bΙ是 (bI)-强可解的当且仅当

证明 必要性。令AΙx≤bΙ是 (bI)-强可解的。假设式(7)不成立，则有:

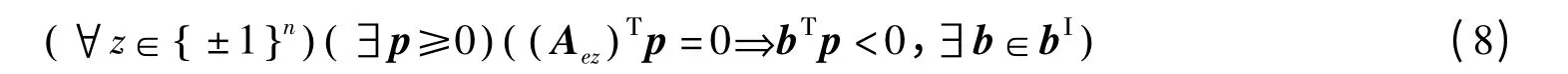
由于向量p的非负性，所以bΤp ＜0 则意味着bΤp ＜0，从而由式(8)得:

由引理3 知式(9)是系统AΙx≤不是弱可解的Farkas型充要条件，即由式(9)可知，AΙx≤不是弱可解。即存在b∈bΙ使得对任意的A∈AΙ不等式Ax≤b 都没有解，因此由定义知系统AΙx≤bΙ不是(bI)-强可解的，矛盾。所以，式(7)成立。

充分性。类似于定理1 充分性的证明，采用反证法，再应用引理3 即可得证。

接下来，给出上述3种情况另一种形式的Farkas型定理，显然对应同一种情况的Farkas型条件之间是等价的。

定理4 区间线性系统AΙx=bΙ是 (bI)-强可行的当且仅当

证明 由定理1可知只需要证明条件(4)成立当且仅当条件(10)成立。

充分性。令式(10)成立。如果向量p 满足，对任意的A∈AΙ都有AΤp≥0，则 (Aze)Τp≥0，这里z=sgn p，展开后得即所以由式(10)得到因此对任意的b∈bΙ都有得证。

定理5 区间线性系统AΙx≤bΙ是 (bI)-强可行的当且仅当

定理6 区间线性系统AΙx≤bΙ是 (bI)-强可解的当且仅当

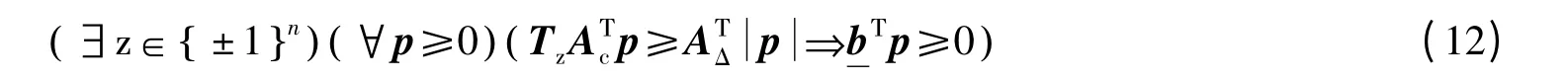
证明 必要性。类似于定理1 充分性的证明，采用反证法，再应用引理4 即得证。

充分性。类似于定理4 充分性的证明，再应用定理3 即可得证。

3 结束语

本文给出了区间线性系统的3种Farkas型定理，为进一步研究区间系统和区间优化提供了理论基础。对区间系统而言，(bI)-强问题总共分为等式的(bI)-强可解、(bI)-强可行、不等式的(bI)-强可解和(bI)-强可行4种情况[5]。而本文只描述了后3种情况的Farkas型充要条件，关于区间线性方程组的(bI)-强可解的简洁实用的Farkas型充要条件还未建立，这也是一个可以继续深入研究的问题。另外，区间优化问题的研究有了长足的发展，比如文献[7]。如何将区间系统的Farkas型定理应用到这些优化问题中去研究解的特性，是一个很有趣的课题。

[1]Rohn J.A Farkas-type theorem for linear interval equations[J].Computing，1989，43(1):93-95.

[2]Karademir S，Prokopyev O A.A short note on solvability of systems of interval linear equations.Linear Multilinear Algebra[J].Linear and Multilinear Algebra，2011，59:(6)707-710.

[3]Rohn J.A Farkas-type theorem for interval linear inequalities[J].Optimization Letters，2014，8(4):1 591-1 598.

[4]Xia M，Li W，Li H.Farkas-type theorems for interval linear systems[J].Linear and Multilinear Algebra，2015，63(7):1 390-1 400.

[5]Li H，Luo J，Wang Q.Solvability and feasibility of interval linear equations and Inequalities[J].linear Algebra and its Applications，2014，463:78-94.

[6]Fiedler M，Nedoma J，Ramík J，et al.Linear Optimization Problems with Inexact Data[M].New York:Springer，2006:35-77.

[7]Luo J，Li W.Strong optimal solutions of interval linear programming[J].Linear Algebra and its Applications，2013，439(8):2 479-2 493.