基于粒子群优化算法的金刚石砂轮磨粒边缘提取
缪晶晶, 崔长彩, 周丽君, 余 卿, 叶瑞芳
(华侨大学机电及自动化学院,福建 厦门 361021)
基于粒子群优化算法的金刚石砂轮磨粒边缘提取
缪晶晶, 崔长彩, 周丽君, 余 卿, 叶瑞芳
(华侨大学机电及自动化学院,福建 厦门 361021)
为了实现对金刚石砂轮磨粒边缘的有效提取,将基于粒子群优化算法的Canny算子应用在金刚石砂轮磨粒的边缘检测上。用最大类间方差作为目标函数,优化Canny算子的阈值,实现边缘的有效提取。分别对实测的单颗磨粒和多颗磨粒进行了边缘提取,实验结果显示该算法可以较好地提取金刚石砂轮磨粒边缘。该方法不需要人为设定阈值,可以实现阈值的自动获取和优化。最后,利用四连通成分和八连通成分与像素总数的比值,将阈值可优化设定的Canny算子与传统的Canny算子以及最大类间方差的方法做对比,结果表明所应用的方法有效地提高了检测的准确性。
磨粒;Canny算子;最大类间方差;粒子群优化算法
砂轮的表面形貌是影响整个磨削加工过程的重要因素之一。砂轮表面磨粒的分布状态,每个磨粒的参数特征会影响砂轮的切削性能。由于砂轮形貌复杂随机,磨粒分布不均使得参数提取变得比较困难。只有采用适当的方法将磨粒从测量数据中提取出来才能对砂轮表面磨粒的出刃高度、静态有效磨粒密度和磨粒间距等参数进行分析[1]。
常用的边缘检测方法主要有:Roberts算子、Sobel 算子、Prewitt 算子、Canny算子等[2]。其中,Canny算子具有信噪比较大、检测精度较高和计算量较小等优点,已经得到广泛应用[3]。但是,Canny算子用Gauss函数作为滤波器,缺点是会造成原图像缓变边缘容易丢失及假边缘现象,针对这些问题,人们开展了相关的研究,并提出了一些改进措施。黄剑玲和郑雪梅[4]利用GCV阈值的小波滤波方法平滑图像去除噪声,然后计算梯度算子的幅值和方向,最后利用抑制极大值和高低阈值的方法提取并连接边缘。赵洁等[5]结合小波融合技术,提出了一种基于改进Canny算子和图像形态学融合的边缘检测方法,应用小波融合技术把改进的Canny算子和图像形态学检测出来的边缘进行图像融合,得到最终的图像边缘。雒涛等[6]根据梯度直方图信息,提出了梯度差分直方图的概念,并且对图像进行自适应分类处理,使得算法不仅不需要人工设定阈值,而且还能有效地避免Canny算法在边缘提取中的断边和伪边缘现象。
针对传统Canny算子存在的边缘丢失和假边缘现象,本文运用粒子群优化(particleSwarm optimization,PSO)的Canny算子边缘检测方法来对砂轮磨粒进行边缘提取。利用粒子群优化算法自动搜索阈值方法获得连接边缘的阈值,使算法在阈值的选择上有了较大的改善。其具体实施的方法是,将最大类间方差(OTSU)公式作为PSO算法的适应度函数,寻找到合适的阈值,以此阈值作为Canny算子的阈值从而实现磨粒边缘提取。
1 粒子群算法改进Canny算子进行边缘提取
1.1 粒子群优化算法的基本原理
Kennedy和Eberhart[7]于1995年提出PSO算法是一种由种群智能方法演化而来的计算技术。此算法是受鸟类觅食行为的启发,假设有一群鸟在随机搜寻一块食物,那么找到食物最简单有效的方法就是搜寻距离食物最近的鸟的周围区域。如今,PSO算法已经被运用到图像处理中[8]。
PSO算法是通过随机产生的一群粒子在空间中搜索迭代来找寻最优解[9]。假设一个由M个粒子(particle)组成的群体(swarm)在 D维搜索空间中以一定的速度飞行,每个粒子在搜索时,综合考虑到了局部最优解和全局最优解,在此基础上进行位置(也就是解)的变化。
第i个粒子的位置表示为:xi=(xi1,xi2,… ,xid,… ,xiD),1≤i≤M,1≤d≤D;第i个粒子的速度表示为:vi=(vi1,vi2,… ,vid,… ,viD),1≤i≤M,1≤d≤D;第i个粒子的局部最优解表示为:pi=(pi1,pi2,… ,pid,… ,piD);群体内(或领域内)的全局最优解表示为:pg=(pg1,pg2,…,pgd,… ,pgD)。
粒子的位置和速度根据式(1)~(2)进行变化:

其中,w为惯性权重;c1和c2为学习因子,正常数;k为迭代次数。惯性权重表明了上一代速度对当前速度的影响。学习因子使粒子具有自我总结和向群体中优秀个体学习的能力,从而向局部最优解和全局最优解靠近。ξ和η是在区间[0,1]内均匀分布的伪随机数。粒子的速度被限制在一个最大速度Vmax的范围内。
1.2 Canny算子的基本原理
Canny把边缘检测问题转变为检测单位函数极大值的问题。在高斯噪声中,一个典型的边缘代表一个阶跃的强度变化。通常Canny算法的具体过程包括[10]:
(1) 采用一维高斯函数作为滤波器对图像进行平滑滤波。
(2) 计算平滑后图像中各点的梯度方向和幅值。
(3) 对梯度幅值进行非极大值抑制,从而保留幅值局部变化最大的点。
(4) 设定双阈值中的高低两阈值,选取边缘点。保留梯度值大于高阈值的点,删除梯度值小于低阈值的点。梯度值介于两阈值间的点,如果与边缘点相邻,那么作为边缘保留,否则删除。
在上述算法流程中,边缘检测的关键是阈值的选取。如果选取的阈值过高将导致边缘断裂不连续,从而丢失边缘信息。相反如果选取的阈值过低将导致提取的边缘中出现过多的伪边缘,甚至将噪声当做边缘提取。所以运用一种方法来选取阈值就显得至关重要。本文采用PSO算法来实现阈值的选取。
1.3 运用粒子群优化算法求取阈值
1.3.1 适应度函数的确定
运用PSO算法的关键是确定适应度函数,本文是将最大类间方差(OTSU)的公式作为其适应度函数。最大类间方差法的原理:将图像分为目标和背景两个部分,通过搜索计算类间方差的最大值,得到最优阈值[11]。对于大小为X×Y的图像,其中用来区分目标和背景的阈值记作 T。N1表示图像中灰度值大于阈值T的像素总和,即目标的像素数。N2表示图像中灰度值小于阈值T的像素总和,即背景的像素数。δ1表示目标像素点数占总像素点数的比例,δ2表示背景像素点数占总像素点数的比例。μ1表示目标的平均灰度值,μ2表示背景的平均灰度值,μ为图像的总灰度均值,类间方差记为g,则有[12]:
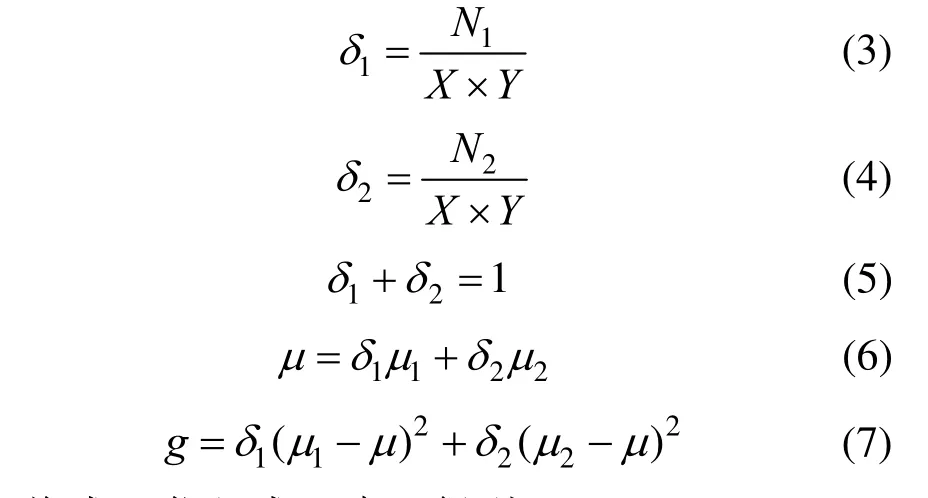
将式(6)代入式(7)中,得到:
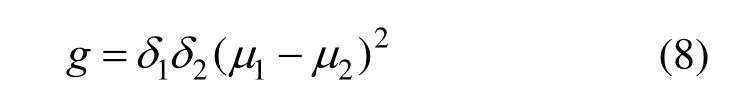
将式(8)作为 PSO算法的适应度函数,通过算法的迭代搜索,找出使得g最大的阈值T的值,作为Canny算法的高阈值来实现边缘检测。
1.3.2 算法计算流程
计算流程包括以下步骤:
步骤 1. 利用白光干涉仪采集表面图像,得到图像的灰度值。将图像灰度值进行归一化处理,使得灰度值变成[0,1]的一组数据。
步骤2. 初始化PSO算法参数并计算适应度函数:初始化粒子群规模M取40,惯性权重的初始值w取0.729 8,最大迭代次数MaxDT取100,学习因子经验值c1、c2取1.496 2。在[0,1]利用随机函数生成40个粒子的初始位置(一组阈值T)xi和初始速度vi。
步骤 3. 粒子移动更新:由式(1)~(2)计算粒子的速度和位置,通过式(8)计算图像的类间方差,并将其作为适应度函数。比较粒子的适应值和局部最优解,如果当前值比局部最优解更优,则将局部最优解变为当前值。比较粒子适应值与全局最优解,如果当前值比全局最优解更优,则将全局最优解变为当前粒子的适应值。如此利用PSO算法求出每个粒子的最佳阈值点和全局最佳阈值点。
步骤4. 算法终止条件:当算法达到最大的迭代次数或适应度函数值达到最大值时则终止迭代,此时最优阈值即为图像的最佳分割阈值T,否则转到步骤3。
步骤5. 输出结果。
1.3.3 改进Canny算子的金刚石砂轮磨粒边缘检测
本文测量仪器选用白光干涉仪。对树脂结合剂砂轮和青铜结合剂砂轮进行测量。在进行磨粒边缘提取时,运用粒子群优化算法得到的阈值作为Canny算法的阈值。图1所示为磨粒边缘提取的流程图。
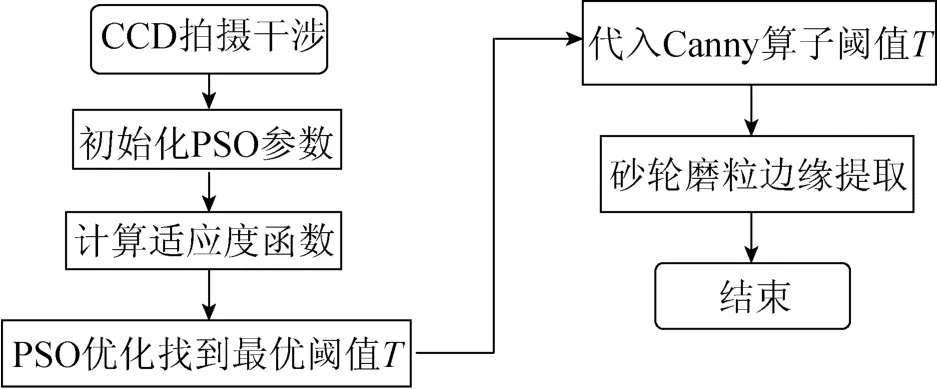
图1 磨粒边缘提取流程图
2 实例分析
2.1 单颗磨粒边缘提取
本文首先选用SDC120(120粒度)树脂结合剂金刚石砂轮。测量仪器选用白光干涉仪。拍摄图像为600×800像素,对应实际尺寸为0.27Mm×0.36Mm。图2为树脂结合剂金刚石砂轮表面形貌的三维轮廓图和俯视图。传统 Canny算子和最大类间方差法(OTSU)得到的磨粒边缘提取分别如图3(a)和图3(b)所示,改进后的Canny算子得到的磨粒边缘提取如图3(c)所示。对比三幅图可以看出传统方法提取磨粒出现过多的伪边缘,甚至将磨粒周围噪声当做边缘提取,改进后的Canny算子提取磨粒伪边缘较少,噪声也基本被消除,效果较好。
2.2 多颗磨粒边缘提取
对于较大范围的多颗磨粒的检测和边缘提取,本文用白光干涉仪对SDC120(120粒度)青铜结合剂金刚石砂轮表面进行测量。利用图像拼接技术,组成一个587×1441像素的图像。图4为青铜结合剂金刚石砂轮表面形貌的三维轮廓图和俯视图。传统Canny算子和最大类间方差法得到的磨粒边缘提取如图5(a)和图5(b)所示,改进后的磨粒边缘提取如图5(c)所示。对比改进前后的提取图可以看出传统Canny算子和最大类间方差法的磨粒边缘提取都出现了过多的伪边缘和噪声,改进后的Canny算子可以较好地提取磨粒,并且可以说明本文的方法对多 磨粒同样适用。
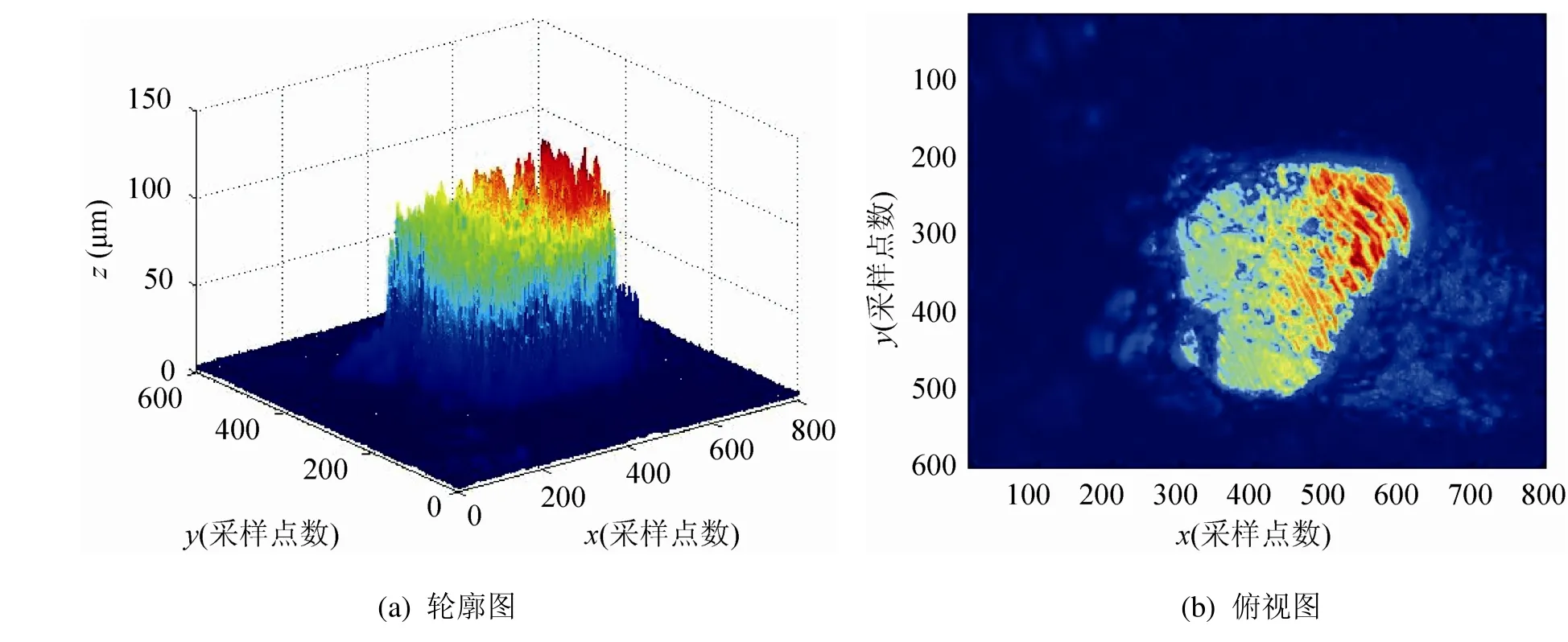
图2 砂轮表面三维轮廓图和俯视图

图3 砂轮磨粒边缘提取图
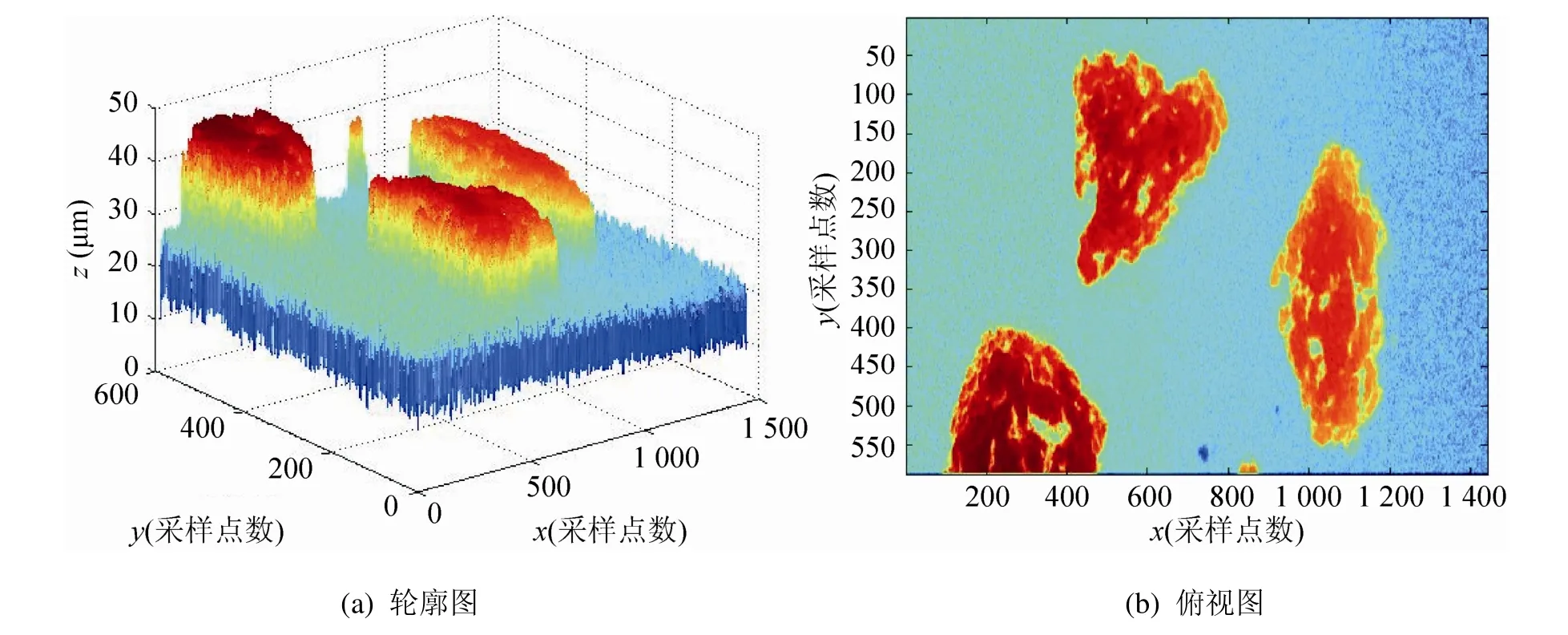
图4 砂轮表面三维轮廓图和俯视图

图5 砂轮磨粒边缘提取
2.3 大面积磨粒边缘提取
由于仪器测量范围的限制,本文采用模拟的砂轮表面来实现大面积多磨粒边缘提取。用四棱锥体模拟磨粒,组成一个1024×1024像素的大范围多磨粒砂轮表面。图6为砂轮表面形貌的三维轮廓图和俯视图。传统Canny算子和最大类间方差法得到的磨粒边缘提取如图7(a)和图7(b)所示,改进后的磨粒边缘提取如图7(c)所示。对比改进前后的提取图可以看出传统Canny算子和最大类间方差法的磨粒边缘提取都出现了过多的伪边缘和噪声,改进后的Canny算子可以较好地提取磨粒,如此可以说明本文的方法对大面积多磨粒的边缘提取同样适用。
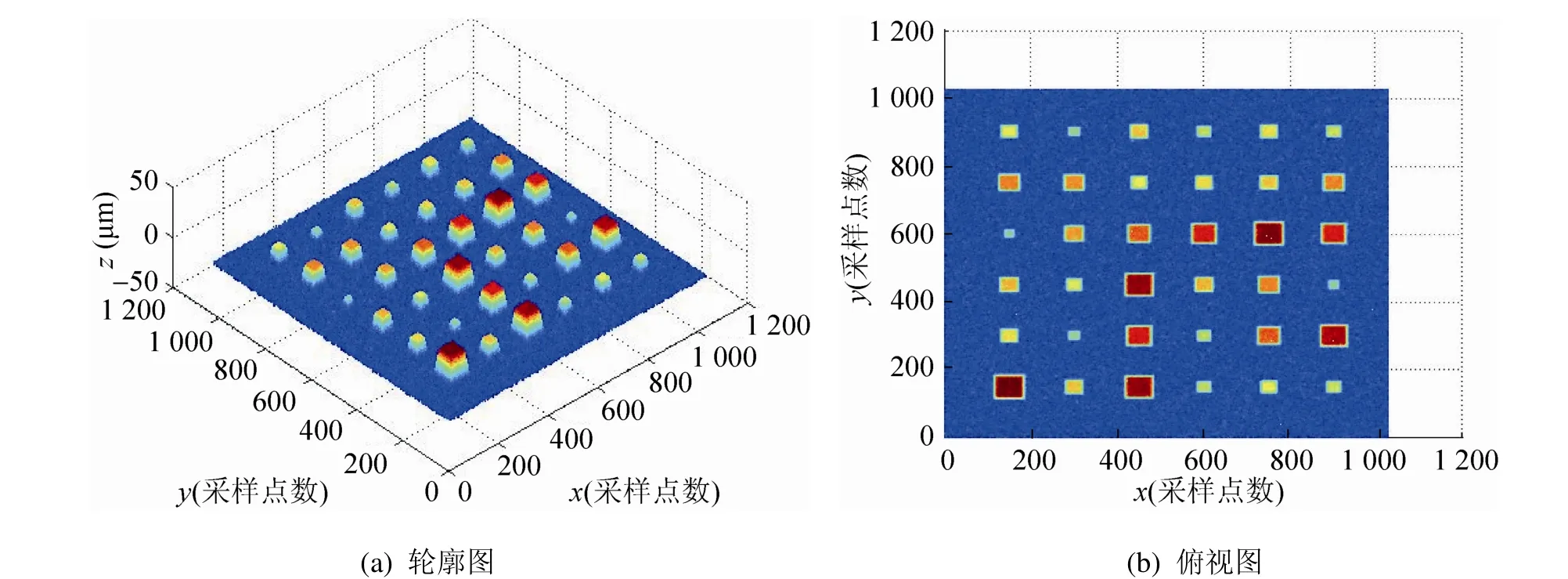
图6 模拟砂轮表面三维轮廓图和俯视图

图7 模拟砂轮磨粒边缘提取图
2.4 算法评价
为了更加全面地对比磨粒边缘提取的效果,将传统的 Canny算子以及最大类间方差法(OTSU)和基于PSO的Canny算子3种方法所选取出的阈值进行对比,如表1所示。并将3种方法的用时进行对比,如表2所示。由结果可看出改进后的方法用时明显增大,但效果比传统方法更好。最后将3种方法的计算结果进行对比,具体方法如下:

表1 边缘提取阈值对比
对磨粒提取后的边缘图像的二值化图像,统计其边缘像素总数(A),4连通数(B)和 8连通数(C),其中C/A越小,证明进行磨粒边缘提取时得到的边缘的连续性越好,间断越少;C/B越小,证明单像素边缘所占的比例越大,越符合单边响应准则[13]。表3为不同磨粒改进前后边缘提取效果的对比。
从表1中可以看出,传统的Canny算子是通过人工设置的阈值来提取边缘,无法针对不同的对象进行变化。改进之后的Canny算子可以针对不同的对象进行阈值自适应的选取,得到的阈值能够较好地提取边缘。

表2 边缘提取所需时间对比

表3 边缘检测效果对比
由表2可看出改进后的方法由于需要迭代选取最适合的阈值,所以用时明显增大,但提取效果比传统方法好。
从表3中可以看出改进后C/A,C/B的值较传统方法得到的值小,说明提取的边缘连续性好、符合单边响应准则,而且能更好地保持细节和减少伪边缘的产生。
3 结 论
本文运用PSO的Canny算子边缘检测方法来对砂轮磨粒进行边缘提取。利用改进的最大类间方差阈值方法获得连接边缘的阈值,使算法在阈值的选择上有了较大的改善。通过验证,改进后Canny算法不仅适用于单颗磨粒,而且适用于多颗磨粒。综合比较了传统的Canny算法、最大类间方差算法和基于PSO的Canny算法的阈值选取和用时长短,并利用4连通成分和 8连通成分与像素总数的比值,将阈值可优化的Canny算子与传统的Canny算子以及最大类间方差法做对比,结果表明改进的算法有效地提高了边缘提取的准确性。
[1] 霍凤伟, 金洙吉, 康仁科, 等. 细粒度金刚石砂轮表面磨粒识别研究[J]. 大连理工大学学报, 2007,47(3): 1177-1180.
[2] 王智文. 几种边缘检测算子的性能比较研究[J]. 制造业自动化, 2012, 34(6): 14-16.
[3] 宗露艳, 吴 陈. 一种改进的Canny算子边缘检测算法[J]. 现代电子技术, 2011, 34(4): 104-106.
[4] 黄剑玲, 郑雪梅. 一种改进的基于Canny算子的图像边缘提取算法[J]. 计算机工程与应用, 2008,44(25): 170-172.
[5] 赵 洁, 李 玮, 郝志鹏, 等. 基于改进 Canny算子与图像形态学融合的边缘检测方法[J]. 微型机与应用, 2011, 30(10):44-46.
[6] 雒 涛, 郑喜凤, 丁铁夫. 改进的自适应阈值 Canny边缘检测[J]. 光电工程, 2009, 36(11): 106-111.
[7] Kennedy J, Eberhart R. particle swarm optimization [C]//International Conference on Neural Networks, USA, IEEE Press, 1995: 1942-1948.
[8] 王洪涛, 李 丹. 基于改进粒子群算法的图像灰度增强研究[J]. 图学学报, 2013, 34(6): 87-92.
[9] 杨 维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-92.
[10] 金 刚. 自适应Canny算法研究及其在图像边缘检测中的应用[D]. 杭州: 浙江大学, 2009.
[11] 唐路路, 张启灿, 胡 松. 一种自适应阈值的 Canny边缘检测算法[J]. 光电工程, 2011, 38(5): 127-131.
[12] Otsu N. A thresholdSelectionMethod from gray-leve histogram [J]. IEEE Transactions Actions onSMC, 1979, (9): 652-655.
[13] 林 卉, 赵长胜, 舒 宁. 一种新的基于连通成分的边缘评价方法[J]. 现代测绘, 2003, 26(2): 8-11.
Grains Detection of Diamond Grinding Wheel Based on ParticleSwarm Optimization
Miao Jingjing, Cui Changcai, Zhou Lijun, Yu Qing, Ye Ruifang
(College ofMechanical Engineering and Automation, Huaqiao University, Xiamen Fujian 361021, China)
In order to effectively identify the abrasive grains on a diamond grinding wheel, the Canny operator based on particleSwarm optimization was applied on the grain edge detection. WithMaximum ClassesSquare Error (OTSU) as the objective function, the threshold of the Canny operator was optimized for grains detection. The edges of aSingle grain and a group of grains were detected using theMethod respectively. The results of the examplesShow that the algorithm can identify grains of diamond grinding wheel effectively. TheMethod can automaticallySet and optimize the threshold of Canny operator which traditionally need to beSet artificially. Finally, the threshold optimized Canny operator was compared with the traditional Canny operator and OTSU by using the ratio of the pixels number of four and eight connected areas to the total number of pixels. The resultsShow that the threshold optimized Canny operator can improve the accuracy of detection.
grains; Canny operator;Maximum classesSquare error; particleSwarm optimization
TP 391
A
2095-302X(2015)02-0238-06
2014-04-13;定稿日期:2014-08-25
国家自然科学基金资助项目(51475176, 51235004);教育部“新世纪优秀人才支持计划”资助项目(NCET-10-0116)
缪晶晶(1990–),女,安徽马鞍山人,硕士研究生。主要研究方向为砂轮表面的测量与评价。E-mail:miaojingjing0411@163.com
崔长彩(1972–),女,山东青岛人,教授,博士。主要研究方向为精密测量技术及仪器。E-mail:cuichc@hqu.edu.cn

