异构CAD数据交换中样条草图的处理方法

张德军， 何发智， 李小霞

(1. 武汉大学计算机学院, 湖北 武汉430072；2. 华中农业大学理学院, 湖北 武汉430070)

异构CAD数据交换中样条草图的处理方法

张德军1， 何发智1， 李小霞2

(1. 武汉大学计算机学院, 湖北 武汉430072；2. 华中农业大学理学院, 湖北 武汉430070)

针对现有异构CAD系统间的产品数据交换方法对样条草图处理不足问题，提出了支持样条草图参数化交换的草图数据交换构架。将草图数据交换分为简单参数草图数据交换和复杂参数草图数据交换。重点分析了复杂参数草图数据交换问题，通过引入 Hausdorff距离作为适应度评价方法，构建了基于粒子群优化求解的样条草图参数化交换算法，利用曲率自适应学习因子来避免局部最优解，使得不同曲率区域的参数点位置合理分布。所提方法在异构CAD系统间进行了实验测试，结果证明了本方法的有效性。

异构CAD系统；样条草图；粒子群优化；Hausdorff距离

在协同产品开发过程中，企业使用最多并且最能体现创新知识产权的数字化模型便是各种CAD模型。不同的企业或部门出于经济、效率、工作习惯等方面的考虑，往往会选用具有不同特点的三维造型工具或者其他数字化工具，从而产生了大量的异构CAD模型。而异构CAD模型的数据交换对于工业界和学术界来说都具有挑战性[1]。当前，异构CAD模型的数据交换方法主要分为 2大类：基于几何模型的数据交换和基于特征模型的数据交换[2-3]。

通过基于几何模型的数据交换所得到的几何数据中不包含高层语义信息(设计意图、特征等)，使得在目标CAD系统端无法对原设计进行参数化的编辑、修改和再设计活动。与基于几何模型的数据交换相比，通过基于特征模型的数据交换所得的模型中保存了用户的设计意图、特征及参数化信息等高层语义信息，从而保证了用户能够使用异构CAD系统对交换所得的模型继续进行参数化编辑、修改和再设计活动。

基于特征模型的异构 CAD系统数据交换研究，最早可以追溯到普渡大学Hoffmann教授所进行的EBrep(Editable Brep)研究。EBrep希望能够通过对造型活动如特征创建与特征修改等进行文本式过程描述，得到与底层几何造型引擎无关的、完整的、无二义性和可编辑的特征模型[4]。

Pratt等[5-7]试图在几何交换标准集合基础上进行扩展，增加了若干支持基于特征数据交换的STEP标准。该方法所能实现的实例和支持的系统都非常有限，并且未说明如何处理样条草图参数化交换问题。Mun等[8]受数据库中通过日志文件恢复数据机制的启发，提出了宏命令方法。Choi等[9]完善了宏命令方法的关键步骤，并通过自行研制的 TransCAD系统实现宏文件中的造型命令与标准CAD系统中宏文件中的标准造型命令之间的映射。Li等[10]实现了不同领域 CAD系统之间的参数化信息交换。宏命令方法对样条草图参数化交换未给出有效的解决方法。Rappoport等[11-13]提出一种基于通用产品表示(universal product representation，UPR)的参数化特征交换方法，UPR方法采用的是一种改进的中性架构，它在中间数据库中存放的是各CAD系统所支持的数据或操作类型的并集，而不再是它们的交集。与主要关注特征过程表示及其交换的研究取向不同，Li等[14-16]提出基于过程恢复的特征数据交换方法，重点研究过程恢复这一难题，有利于处理复杂特征、边界模型中拓扑元素匹配、边界模型之外被引用的参考信息的匹配等。

以上代表性方法中，对样条草图的处理，主要采用几何替代，失去了特征数据交换的优点[9]。基于上述问题，本文提出了支持样条草图参数化交换的草图数据交换构架，将草图数据交换分为简单参数草图数据交换和复杂参数草图数据交换。针对复杂参数草图参数化交换问题，构建了基于粒子群优化求解的样条草图参数化交换算法。本文详细介绍了草图参数化交换的理论依据、总体框架和算法设计。所提方法在异构CAD系统间进行了实验测试，结果证明了本方法的有效性。

1 样条草图交换问题的提出

主流的CAD系统(Pro/E、SolidWorks、UG和CATIA)的草图功能可以分为 2类：简单参数草图(比如：Line、Rectangle、Circle等)和复杂参数草图(样条草图)。

样条草图不仅是异构CAD系统间唯一的复杂参数草图，而且也是唯一的奇异草图。样条草图是CAD系统对标准样条曲线的高层次封装，不同于底层的数学表达，是一种充分反映了设计者的设计意图的高层语义信息的封装，设计人员通过控制其高层参数，可以设计出各式各样的几何形状。主流的CAD系统为用户提供的样条草图的控制参数如表1所示，其中“√”表示该CAD系统提供该控制参数， 而“×”则表示不提供该控制参数。

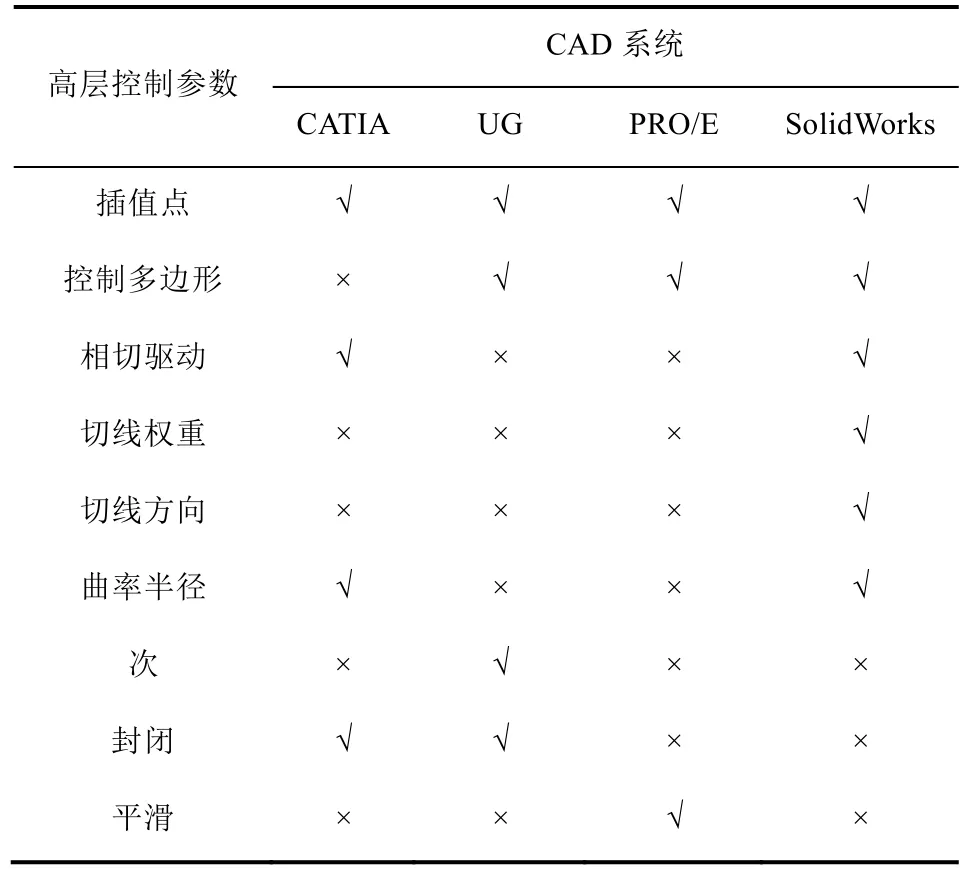
表1 不同CAD系统中样条草图参数

从表1得知，异构CAD系统间样条草图的高层参数互不一致，当进行样条草图参数化交换，从源CAD系统提取的高层参数，在目标CAD系统中找不到全部都能对应的高层参数，这给样条草图基于参数化的数据交换带来了困难。如果强制基于源样条草图的部分参数来驱动目标样条草图，所得到的几何形状则严重失真。

2 草图参数化交换方法

根据草图功能分类，将异构CAD系统间草图数据交换分解为：简单参数草图数据交换和复杂参数草图数据交换。

2.1 简单参数草图数据交换

主流的商业化CAD系统提供了基于特征的参数化造型技术，但对草图及参数没有统一的标准，造成了造型结果不一致。通过比较发现异构CAD草图间的不一致主要有两个方面：草图功能不一致和草图参数不一致。

异构CAD系统间简单参数草图数据交换中草图功能与草图参数之间关系如表2所示。

表2 简单参数草图中功能与参数关系

其中，c表示异构CAD系统间草图功能一致，比如：CATIA和SolidWorks中的line、circle等具有相同的功能。与之相反，表示草图功能不一致，比如：SolidWorks中有polygon，而在Pro/E中没有polygon，但可以通过多个line联合实现。p表示异构CAD系统间草图参数一致，比如：UG和CATIA的circle的参数都是圆心和半径，对于这类参数可以一一对应。表示参数不一致，需要进行转换。

由此，异构CAD系统间简单参数草图数据交换分为3类交换关系，可表示为：

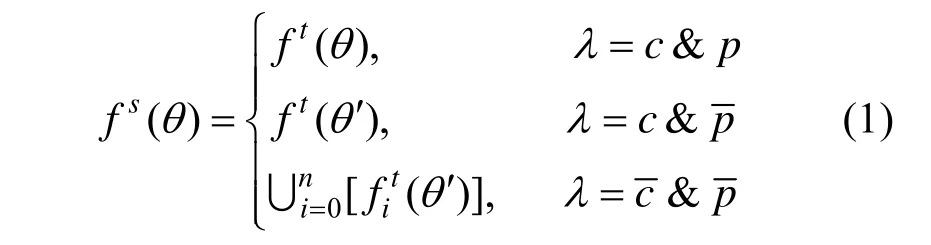
其中， fs(ft)表示源(目标)系统的草图功能，θ表示源参数，θ′表示转换之后的参数。

2.2 复杂参数草图数据交换

样条草图是异构CAD系统间唯一的复杂参数草图，不能简单的以草图功能不一致和草图参数不一致来描述异构CAD样条草图间的差异，不能通过式(1)进行样条草图数据交换。如果强制通过式(1)进行样条草图数据交换(基于源样条草图的参数来驱动目标样条草图)，所得到的目标样条草图的几何保真度较低。

本文提出在目标CAD系统端寻找一组高层参数(插值点)来拟合源样条草图的几何信息。异构CAD样条草图拟合策略如下：

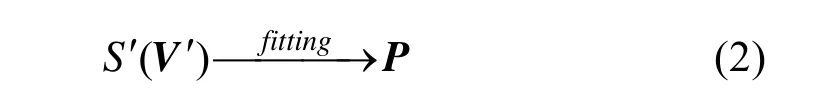
式中，S′和 V′分别表示目标 CAD系统端的样条草图及高层参数，P表示源样条草图S的几何信息。

异构CAD样条草图拟合步骤如下：

步骤 1. 获取源样条草图S的底层几何信息(离散点集 p={p1,p2,…,pn})；

步骤2. 在目标CAD系统端寻找一组最优高层参数集 V′拟合离散点集P；

步骤3. 利用高层参数集 V′重构样条草图S′。

然而，在异构CAD样条草图拟合过程中，其高层参数(插值点)位置分布和数量的确定是一个大空间寻优的问题，基本上难以通过人工交互的方式解决。本文提出了基于粒子群优化求解的样条草图参数化交换算法，根据源样条草图的几何信息，在目标CAD系统中自动恢复出具有等价几何的目标样条草图。

3 算法设计

3.1 标准粒子群算法

粒子群算法中的粒子以时间为单位进行连续迭代，并在迭代过程中，通过跟踪两个“极值”来更新自己的位置[17]。第一个就是粒子本身所找到的最优解，这个解叫做个体极值另一个极值是整个群体到目前为止找到的最优解，这个极值是全局极值当群体飞行到时刻 t+1，第i个粒子的速度和位置的更新由以下公式给出[18]：

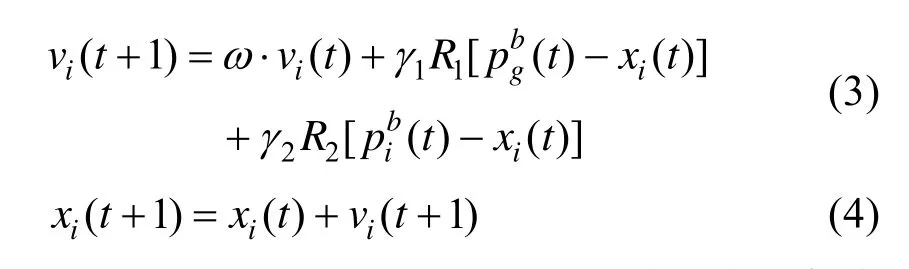
式中，i=1,2,… ,k ；xi(t)和 vi(t)分别表示第i个粒子在t时刻的位置和飞行速度；ω为惯性权重系数用来衡量t时刻粒子速度对 t+1时刻速度影响程度；γ1和 γ2称为加速因子； R1和R2为[0, 1]区间的均匀分布的随机数。

3.2 粒子的编码方案

种群中的粒子表示目标样条草图S′的高层参数集 V′的潜在解。种群包含k个粒子，每个粒子的搜索空间为n维(对应于目标样条草图S′插值点个数)。种群的编码方案及粒子的约束条件如下所示：

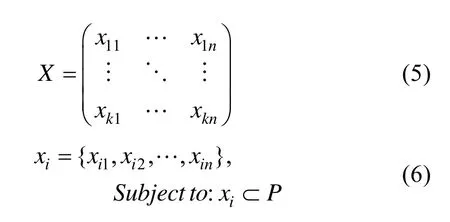
其中，式(6)的约束条件表示从源样条草图S的离散点集P中随机抽取n个点作为目标样条草图S′的一个候选高层参数集。

3.3 适应度

适应度值是判断粒子群迭代好坏的依据。粒子即插值点集 V′的实值表达，直接用于重构目标样条草图S′，本文将目标样条草图S′与源样条草图S的相似度作为粒子适应度评价标准。

Hausdorff距离表征了两个点集之间的相似程度[19]。给定源样条草图S的点集和目标样条草图S′的点集则 P和 p′之间的Hausdorff距离定义为[20]：

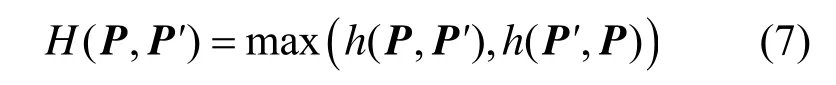
其中：

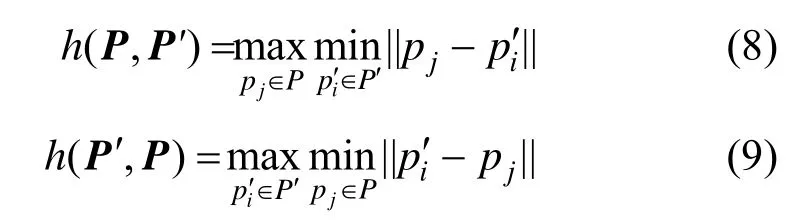
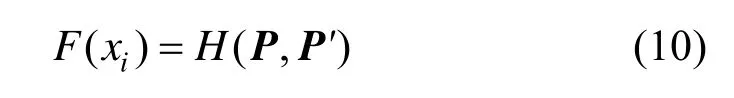
3.4 曲率自适应学习因子

如图 1所示，曲率较大区域插值点分布较为密集，曲率较小区域插值点分布较为稀疏。粒子维度的分布情况类似，通常更多的维度聚集在曲率较大的区域，精确计算这些维度的位置分布及数量，有利于找到全局最优解。

因此，本文算法包含了基于曲率的自适应加速因子方法，根据粒子分量的曲率值自适应的调整加速因子 γ1和 γ2，使得分布在曲率较大区域的分量具有相对较大的个体认知项，增强该区域分量的全局搜索能力，从而使得曲率较大区域的插值点位置分布更加合理，有效避免粒子陷入局部最优；反之，分布在曲率较小区域的分量具有相对较大的社会项，增强该区域分量的局部搜索能力。通过公式表达如下：

其中，γmax，γmin是常数，是样条草图S最大(小)曲率值，c(xid)是xid所对应的曲率值。

3.5 算法流程

根据上述算法思想，基于粒子群优化求解的异构CAD样条草图参数化交换算法描述如下：

算法. 粒子群算法流程

输出：目标样条草图S′插值点集

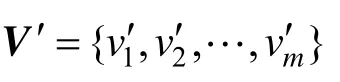
步骤1. 初始化群体X

步骤2. while (not termination condition) do

步骤3. for i=1 to k do

4 实际应用及性能分析

4.1 实际应用

本文提出的草图的处理方法在本课题组开发的异构CAD系统参数化特征交换平台上进行了验证。实验硬件平台配置Intel酷睿i3(3.3 GHz)，8 G内存，运行Windows 7操作系统的台式PC。

图 2给出了基于该平台在SolidWorks和CATIA之间进行压气机转子毛坯参数化交换比较实验。如图2(a)所示，在SolidWorks中设计一个草图(包含简单参数草图和复杂参数草图)；图2(b)是采用直接参数化交换方法在CATIA的重构的草图(在CATIA中利用SolidWorks中源样条草图的插值点直接重构目标样条草图)；图 2(c)是采用本文方法在CATIA中重构的草图。图2(b)和图2(c)的重构草图与图2(a)的源草图之间的Hausdorff距离分别为3.277和0.120。

利用图2(a)中草图，在SolidWorks造型的压气机转子毛坯，如图 2(d)所示。利用图 2(b)和图2(c)中的草图，在CATIA中造型的压气机转子毛坯分别如图 2(e)和图 2(f)所示。对图 2(d)～(f)中的压气机转子毛坯进行表面曲率分析，结果如图2(g)～(i)所示。通过表面曲率比较，可知采用直接参数化交换方法得到的重构模型与源模型之间几何保真度较低，采用本文方法得到的重构模型与源模型之间的几何保真度较高。

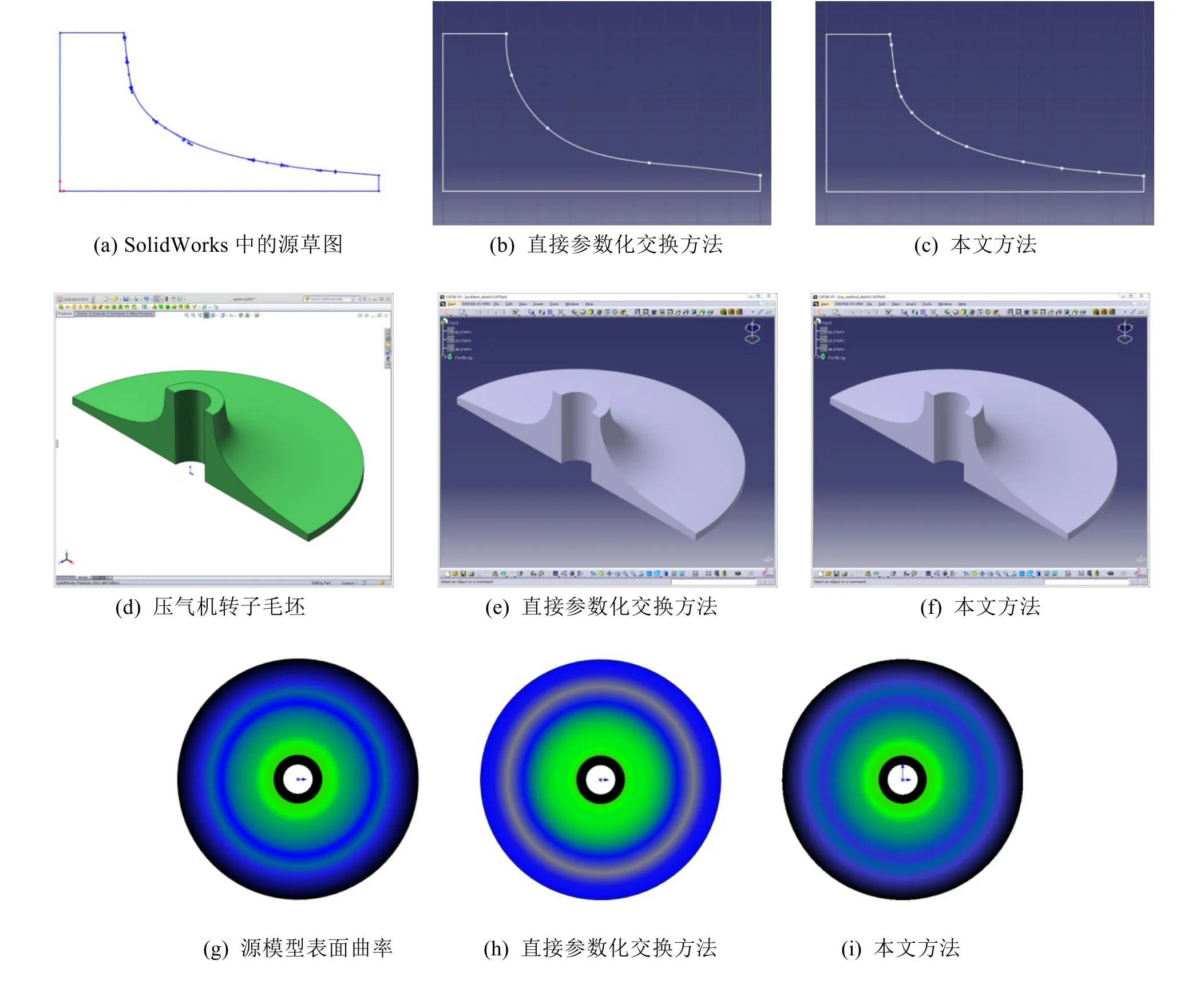
图2 样条草图参数化交换实例一

为了进一步验证本文方法的可靠性，本文对更加复杂的模型进行了参数化交换实验。如图3(a)，在SolidWorks中实例化了一个复杂模型，包含2个Extrude特征，分别对应的草图为简单参数草图(Circle)和复杂参数草图(样条草图)。采用直接参数化交换在CATIA得到的重构模型，如图3(b)所示；采用本文方法在CATIA得到的重构模型，如图3(c)所示。非常明显，通过本文方法所得到的重构模型在几何保真度方面优于直接参数化交换方法。

对上述复杂模型交换实例中的草图交换情况进一步进行分析。源样条草图包括11个插值点，如图 3(d)所示。采用直接参数化交换方法得到的样条草图(包括 11个插值点)，如图 3(e)所示。采用本文方法在CATIA中重构的样条草图(包括30个插值点)，如图 3(f)所示。将采用两种不同方法得到的目标样条草图与源样条草图进行相似性比较，Hausdorff距离分别为16.780和0.573。

实验结果表明，直接参数化交换方法虽然实现了异构CAD系统间样条草图参数化交换，但交换前后的样条草图相似度较低，本文方法实现了异构CAD系统间样条草图参数化交换，并且保证了草图的几何相似度。

图3 样条草图参数化交换实例二

4.2 算法性能分析

对实例一中的样条草图参数化交换中粒子群算法的性能进行分析，结果如图4所示。粒子群算法性能评估采用如下方法：①评估粒子群算法在不同搜索维度情况下，分别进行 300次迭代，适应度值变化情况。②评估粒子群算法在相同拟合误差之下，插值点个数与迭代次数的关系。粒子群算法各个参数设置为：种群个数为40，惯性系数为1，加速因子分别为1.0和0.3。

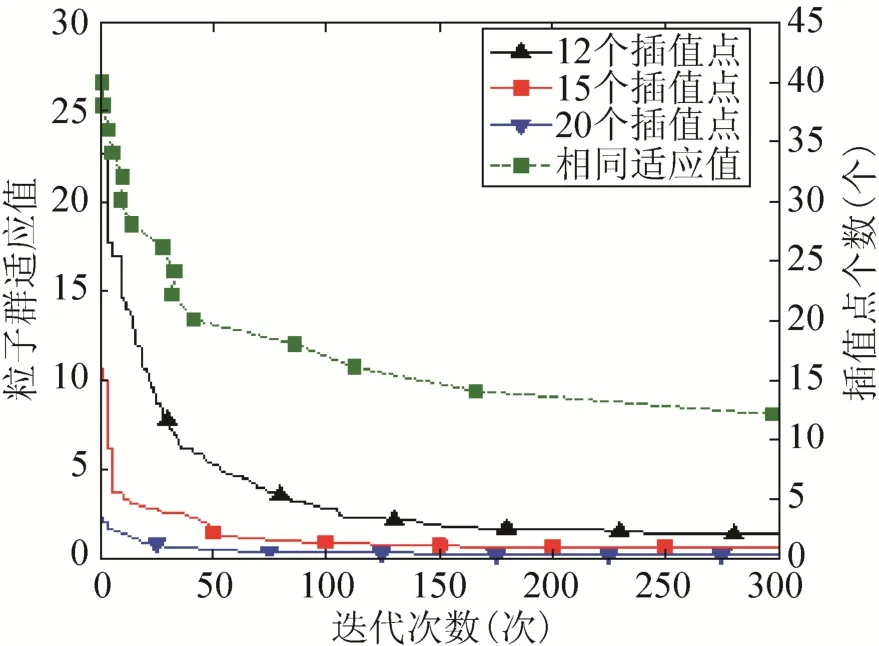
图4 粒子群算法性能分析

从实验结果可以得出以下结论：①当n值越大，拟合误差越小(从用户角度出发，样条草图中插值点过多会使得样条草图基于特征的修改和再设计变得不容易)。②在相同拟合误差之下，迭代次数与样条点个数成反比关系。

5 结 论

针对目前基于特征模型的数据交换对异构CAD样条草图处理不足问题，提出了支持样条草图参数化交换的草图数据交换构架，构建了基于粒子群优化求解的样条草图参数化交换算法。实验证明本文方法的有效性，与基于几何模型的数据交换方法和直接参数化交换方法相比，不仅维护了样条草图的几何相似度，又能使得交换之后样条草图具备基于特征的参数化编辑、修改和重用能力。

[1] 高曙明, 何发智. 异构CAD系统集成技术综述[J].计算机辅助设计与图形学学报, 2009, 21(5)：561-568.

[2] TessierS, Wang Yan. Ontology-based featureMapping and verification between CADSystems [J]. Advanced Engineering Informatics, 2013, 27(1)： 76-92.

[3] Hoffmann C,Shapiro V,Srinivasan V. Geometric interoperability via queries [J]. Computer-Aided Design, 2014,46： 148-159.

[4] Chen Xiangping, Hoffmann CM. Towards feature attachment [J]. Computer-Aided Design, 1995, 27(9)：695-702.

[5] PrattM J, Anderson B D, Ranger T. Towards theStandardized exchange of parameterized feature-based CADModels [J]. Computer-Aided Design, 2005, 37(12)：1251-1265.

[6] PrattM J, Kim J. Experience in the exchange of proceduralShapeModels using ISO 10303 (STEP) [C]// Proceedings of the 2006 ACMSymposium onSolid and PhysicalModeling. New York, USA, 2006： 229-238.

[7] Kim J, PrattM J, Iyer R G, et al.Standardized data exchange of CADModels with design intent [J]. Computer-Aided Design, 2008,40(7)： 760-777.

[8]Mun D, HanS, Kim J, et al. ASet ofStandardModeling commands for the history-based parametric approach [J]. Computer-Aided Design, 2003, 35(13)： 1171-1179.

[9] Choi G H,Mun D, HanS. Exchange of CAD partModels based on theMacro-parametric approach [J]. International Journal of CAD/CAM, 2009, 2(1)： 13-21.

[10] Li Jinggao, Kim B C, HanS. Parametric exchange of roundShapes between aMechanical CADSystem and aShip CADSystem [J]. Computer-Aided Design, 2012,44(2)： 154-161.

[11] Rappoport A. An architecture for universal CAD data exchange [C]//Proceedings of the Eighth ACMSymposium onSolidModeling and Applications. New York, USA, 2003： 266-269.

[12] Rappoport A,SpitzS, EtzionM. One-dimensionalSelections for feature-based data exchange [C]// Proceedings of the 2005 ACMSymposium onSolid and PhysicalModeling. New York, USA, 2005： 125-134.

[13] Rappoport A,SpitzS, EtzionM. Two-dimensionalSelections for feature-based data exchange [C]// Proceedings of the4th International Conference on GeometricModeling and Processing.Springer-Verlag, 2006： 325-342.

[14] Li Xiaoxia, Cai Xiantao, He Fazhi, et al. Retrieval and reconstruction of heterogeneous feature data for collaborative design [C]//Proceedings of the 2010 14th International Conference on ComputerSupported Cooperative Work in Design.Shanghai, China, 2010, 553-558.

[15] Li Xiaoxia, He Fazhi, Cai Xiantao, et al. CAD data exchange based on the recovery of featureModelling procedure [J]. International Journal of Computer IntegratedManufacturing, 2012, 25(10)： 874-887.

[16] Li Xiaoxia, He Fazhi, Cai Xiantao, et al. AMethod for topological entityMatching in the integration of heterogeneous cad systems [J]. Integrated Computer-Aided Engineering, 2013, 20(1)： 15-30.

[17] 陈 翔, 顾 庆, 王子元, 等. 一种基于粒子群优化的成对组合测试算法框架[J]. 软件学报, 2011, 22(12) ：2879-2893.

[18] 胡 捷, 崔长彩, 黄富贵. 基于动态改变权重粒子群算法的球度误差评定[J]. 图学学报, 2012, 33(5)：99-103.

[19] Chen Xiaodiao,Ma Weiyin, Xu Gang, et al. Computing the Hausdorff distance between two B-spline curves [J]. Computer-Aided Design, 2010,42(12)： 1197-1206.

[20] 张松枝, 王旭辉, 唐 烁. 三次 Bezier曲线与圆弧有重合点时的Hausdorff距离[J]. 图学学报, 2013, 34(2)：72-75.

SplineSketch Exchange between Heterogeneous CADSystems

Zhang Dejun1, He Fazhi1, Li Xiaoxia2
(1.School of ComputerScience and Technology, Wuhan University, Wuhan Hubei430072, China; 2. College ofScience, Huazhong Agricultural University, Wuhan Hubei430070, China)

ExistingMethods of product data exchange between heterogeneous CADSystems do notSatisfySplineSketch exchange. This paper proposes a feature-basedSplineSketch exchangeMethod and divides feature-basedSketch exchange intoSimple one and complex one. The problem ofSplineSketch exchange is analyzed and theMethod forSplineSketch fitting based on particleSwarm optimization is proposed. The Hausdorff distance is introduced to calculate the fitness of each particle. It improves the acceleration coefficients based on curvature for avoiding the local optimum, whichMakes the location distribution of interpolation pointsMore reasonable. Test case ofSplineSketch exchange between commercial CADSystems using the proposed approach is given. Experimental resultsShow that proposed approach can be well used to resolve the problem ofSketch exchange.

heterogeneous CADSystems;SplineSketch; particleSwarm optimization; Hausdorff distance

TP 391.7

A

2095-302X(2015)02-0215-07

2014-10-08；定稿日期：2014-10-24

国家自然科学基金资助项目(61472289，61211140348)

张德军(1982–)，男，四川广元人，博士研究生。主要研究方向为异构CAD数据交换、计算机图形学。E-mail：zhangdejun@whu.edu.cn

何发智(1968–)，男，湖北武汉人，教授，博士。主要研究方向为CSCW、计算机图形学、数字图像处理。E-mail：fzhe@whu.edu.cn