求解无约束优化问题的一种新的谱共轭梯度法

汪丹戎，陈忠，张毅 （长江大学信息与数学学院，湖北 荆州434023）

考虑求解无约束优化问题：

这里f（x）：Rn→R为连续可微函数。求解共轭梯度算法的迭代格式如下：

其中，gk＝▽f（xk）为f（x）在xk处的梯度；dk搜索方向；αk≥0为步长因子；βk为谱系数。

不同的βk与αk构成不同的共轭梯度法，如FR方法［1］、HS方法［2］、PRP方法［3］、 CD方法［4］、LS方法［5］、DY方法［6］的参数βk的表达式分别为：

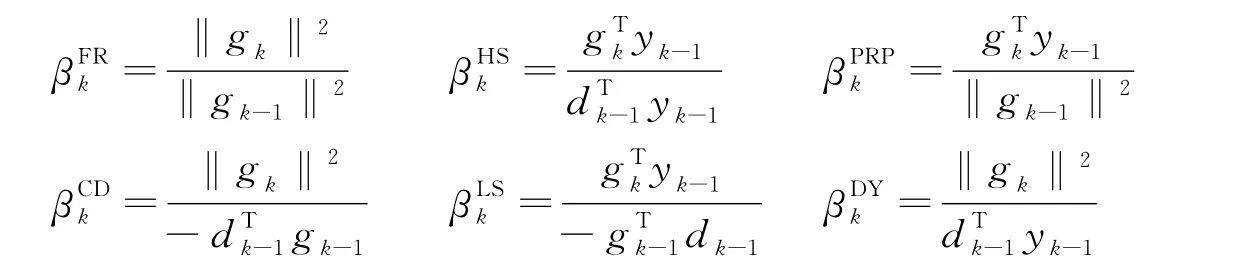
式中，‖·‖ 为欧式范数，yk－1＝gk－gk－1。

在上述几种方法中，PRP、HS和LS方法数值性能良好，但不具有很好的全局收敛性，而FR、CD和DY方法具有良好的收敛性，但数值表现却一般。不少研究者将βk作出改进，设计出了不同效果的算法［7，8］。2001年，Birgin和Martinez［7］将谱共轭梯度和共轭梯度第一次结合起来，提出了谱共轭梯度算法。谱共轭梯度的迭代公式如下：

2007年，YAO，WEI和HUANG［8］对βLSk进行改进，提出了一种的新的βk公式：

该算法每次迭代都可以产生一个充分下降方向，并且在Wolfe线搜索下全局收敛。下面，笔者在文献［8］的基础上，对谱系数βk进行改进，并采用谱共轭梯度算法的的迭代格式，提出了一种新的谱共轭梯度法。

1 算法描述

改进的谱系数βk的表达式如下：

算法描述如下：

步1 给定x∈Rn，ε＞0，0＜ρ＜σ＜1，若 ‖gk‖≤ε，则停止；否则令d1＝－g1，k＝1；

步2 利用Wolfe线搜索准则求得αk：

步3 计算xk＋1＝xk＋αkdk；如果 ‖gk＋1‖ ≤ε， 则停止；

步4 由式 （7）计算βk＋1， 由式 （8）计算θk，由式（6）计算dk；

步5 令k＝k＋1，转步2。

2 充分下降性

定理1 按照βk的新公式（7）和式（8）时，对于所有的k≥1，则有：

证明 利用数学归纳法：

1）当k＝1时，有d1＝－g1，gT1d1＝－‖g1‖2＜0。

2）假设n＝k－1时，式（11）恒成立，即：

由式（10）知：

当n＝k时，由式（7）有：

由式（5）知dk＝－θkgk＋βkdk－1两端与gk作内积，并由（15）可得：

由此可知对于所有的k≥1，gTkdk＜0都成立。

由定理1知，算法在标准Wolfe线性搜索条件，能满足充分下降性。

3 全局收敛性

为证明全局收敛性，假定目标函数f（x）满足以下条件（A）：

1）f（x）在水平集Ω＝｛x∈Rn｜f（x）≤f（x1）｝上有下界；

2）f（x）连续可微且其导数▽f（x）满足Lipschitz条件，即存在常数L＞0，使得：

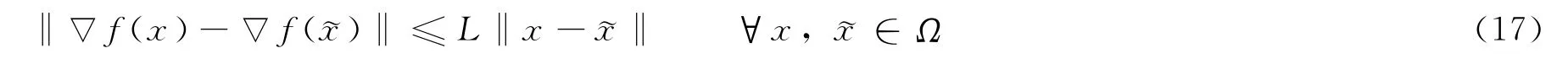
引理1［9］设f（x）和初始点x1满足假设（A），对于式（2）和式（3）产生的迭代，其中dk为下降方向满足gkTdk＜0，步长因子αk应满足式（4），则有：

定理2 设f（x）和初始点x1满足假设（A），对于式（2）和式（3）产生的迭代，步长因子αk应满足式（4），βk由式（6）产生，有：

证明 用反证法。假设结论不成立，则必存在常数c＞0，使得：

对所有的k≥1成立，由式（3）知dk＋θkgk＝βkdk－1，两边取平方模并移项可得：

上式两边除以（gkTdk）2，由式（7）和式（8）可知：

即可得：

由式（20）可知：

即：

这与引理1矛盾，故式 （19）成立，定理2得证。

4 结语

对于无约束优化问题，设计出一种修正的谱共轭梯度算法，证明了该算法产生的搜索方向是充分下降方向，最后还结合Wolfe线搜索及梯度满足Lipschitz条件，证明了算法具有全局收敛性。

［1］ Fletcher R，Reeves C M.Function minimization by conjugate gradients ［J］.The Computer Journal，1964，7 （2）：149～154.

［2］ Hestenes M R，Stieffel E L.Method of conjugate gradient for solving linear systems ［J］.Research Nat Bur Standards，1952，49 （1952）：409～436.

［3］ Polyak B T.The conjugate gradient method in extremal problems ［J］.USSR Computational Mathematics and Mathematical Physics，1969，9 （4）：94～112.

［4］ Fletcher R.Practical Methods of Optimization：Vol.2：Constrained Optimization ［M］.John Wiley﹠Sons，Inc，1987.

［5］ Liu Y，Storey C.Efficient Generalized Conjugate Gradient Algorithms，Part 1：Theory ［J］.Journal of Optimization Theroy and Applications，1991，69 （1）：129～137.

［6］ Dai Y H，Yuan Y.A Nonlinear Conjugate Gradient Method with a strong global convergence property ［J］.SIAM Journal on optimization，1999，10 （1）：177～182.

［7］ Birgin E G，Martimez J M.A spectral conjugate gradient method for unconstrained optimization ［J］.Appl Math optim，2001，43 （2）：117～128.

［8］ Yao S W，Wei Z X，Huang H.A note about WYL’s conjugate gradient method and its apptications ［J］.Appl Math Comput，2007，191 （2）：381～388.

［9］ Zoutendijk G.Nonlinear programming，Computational Methods，in integer and Nonlinear Programming ［M］.North－Holland，Amsterdam，1970.