一种基于GPU并行加速的快速建模方法

罗德新，谢凯，夏巍，廖虎

（长江大学电子信息学院，湖北 荆州434023）

油气资源是关系我国现代化建设全局和国家安全的重要战略资源，在国民经济中也占有非常重要的地位。随着经济的快速发展，世界各国都不同程度地面临着油气需求量急剧增加的问题，因此地质勘探技术的发展，对准确高效的寻找油气储层起着至关重要的作用。三维地质建模是指运用计算机技术，在三维环境下，将空间信息管理、地质解释、空间分析和预测、地学统计、实体内容分析以及图形可视化等工具结合起来以用于地质研究。在复杂地质体的环境下，地质构造复杂，岩性岩相不稳定，地层信息难以获取，这些问题都给地质建模带来很大的影响［1，2］。近年来，我国在油气勘探方面的研究蓬勃发展，开发了具有自主知识产权的地质建模系统［3，4］，其算法构架和功能稳定方面不乏先进性，但是在建模质量、速度及准确度方面与国外同类型软件相比存在明显不足。

随着对复杂地质体的勘探不断深入，复杂几何模型的建模要求也越来越高。在描述极其复杂的地质体时，经常需要对不规则分布的大数据进行地质建模，这些地质模型经常包含断层、褶曲、开挖边界等，其网格通常由成千上万个多边形面片组成.因为这种网格点分布具有很大的随机性，多边形构造复杂，将多边形映射为图像的过程需要大量的计算，因而所需的计算时间相当长，数据存储量也特别大，这对建模算法和建模速度提出了新的要求［5，6］。为此，笔者提出了一种基于GPU并行加速的快速建模方法。

1 建立规则的初始矩形网格模型

对于复杂地质体的网格模型，首先在数据中查找4个边界分布点，根据4个边界分布点确定网格模型的边界值。为了提高其建模的精确度，通过数据中采样点的平均间距来确定网格的划分间距。采样点的X方向的平均间距为x，Y方向的平均间距为y，网格X方向划分间距为Δx，Y方向划分间距为Δy，划分网格如图1所示，则每个网格单元中平均含有采样点数为：

按照矩形搜索范围划分，在修正每个网格节点时，其搜索面积为一个网格单元的面积，所以平均有N个采样点用以修正其中心节点（见图2），采用该方法最终共可得到三角形面的个数为2×（columns×rows）。

图1 标准网格模型划分

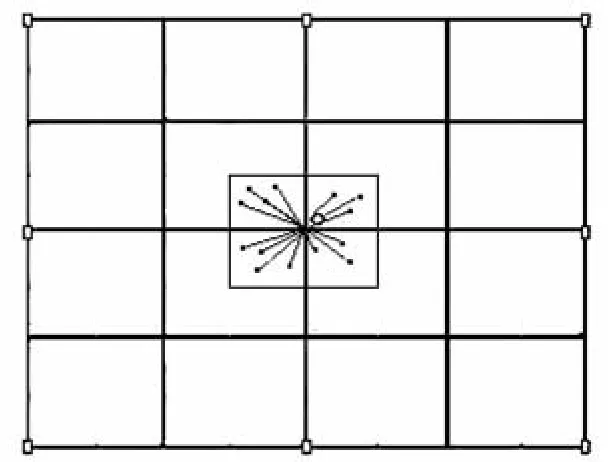
图2 节点修正搜索域划分

2 计算网格模型节点的修正值

设在节点P（r，c）的搜索范围内共搜索到n个采样点，分别用 Q1， Q2， Q3，…，Qn表示， 它们共同决定了P（r，c）点处的值。设Q1，Q2，Q3，…，Qn对P（r，c）点的影响系数分别用ε1，ε2，ε3，…，εn表示， 到P（r，c）点的水平投影距离分别用d1，d2，d3，…，dn表示，

上述n个点共同决定了P（r，c）的值，所以其影响系数之和为1，即：

设P（r，c）矩形搜索范围内所有的采样点与点P（r，c）在水平投影面的距离之和为s，即：

点Qi和P（r，c）在水平面上投影距离用di表示，当di越小，Qi就越接近P（r，c），因而Qi在修正P（r，c）过程中所占的权重越大，其影响系数也越大，反之其影响系数也就越大，即εi∝s－di。

设：

则式（2）可以表示为：

即：

将式（3）代入式（6）可得：

由式（4）、式（7）可得：

因此，按照εi所确定的权重对P（r，c）进行高度修正，其修正后的高度值为：

在修正每一个网格节点时，只需要遍历数据的所有采样点，找到在待修正节点的搜索范围内的采样点即可计算出待修正节点修正后的值。

3 修正算法优化

设某个数据的总采样点数为n，经过预处理后构建了row行、column列的网格模型，平均修正每个节点需要m个采样点，则其修正算法时间复杂度为O（row×column×n＋m），通常数据采样点数在105以上，网格总节点数通常也不小于104，如果在单核CPU上以串行方式执行此算法，其算法时间复杂度将大于O（109），同时在节点修正过程中，至少需要进行2m次乘方运算与m次开方运算，因此，其执行过程非常耗费计算机计算资源，并且耗时长，因而程序运行效率低。针对以上算法的缺点和不足，笔者提出一种常规的优化方法，具体内容如下。

由于要进行建模的数据量较大，采样点较多，所以在所有的采样点中搜索修正网格所需的点会耗时很多。考虑到复杂的存储结构不利于后续并行优化的进行，程序中数据在内存中采用线性表结构存储。当数据量较大时，线性表的排序算法的时间复杂度也相当大。通过分析地质体数据的存储得知，采样点按照行序依次存储，据此为每一个待修正节点建立一个搜索范围索引，这样就能够大大地减小搜索范围，进而提高程序运行效率。

考虑到模型的相似度等因素，取Δx＝8x，Δy＝3y，即平均每个节点由24个采样点计算所得。针对不规则数据每行的采样点数不同的情况，设原始数据平均row行，平均每行采样点数为col，程序中动态建立索引表，每个节点搜索范围起始点索引差约为4col。

4 优化过程并行架构

2007年，NVIDA公司推出CUDA（Compute Unified Device Architecture，统一计算设备构架），在CUDA编程模型［7］中引入了主机与设备的概念。其中CPU为主机，GPU作为设备或协处理器。在主机端主要完成简单数据处理和串行计算，而高度复杂的并行处理计算交由设备完成。CPU与GPU［8］之间的通讯、数据传送等操作则通过CUDA的API存储器管理函数来实现，能够开辟、释放和初始化设备中的存储空间、实现主机与设备间的数据的传输。

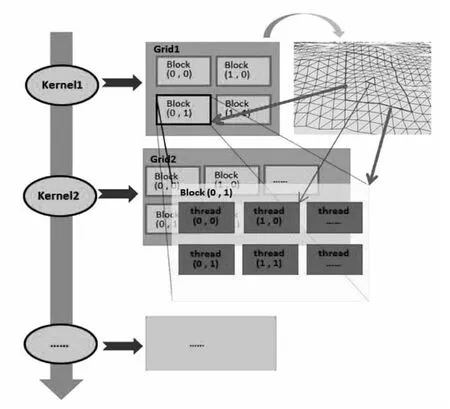
图3 GPU的架构与并行数据分块示意图

当确定了程序中算法的并行部分后，将数据拷贝到设备端。在GPU上运行的函数称为kernel（内核函数），其并不是一个完整的程序，而是CUDA程序中的并行执行部分。图3所示为在CUDA程序中主机端和设备端函数执行的顺序。从图3可以看出，CUDA中的线程被组织成一个二级的层次结构：每个核函数（kernel）对应着一个Grid（栅格），一个Grid（栅格）中包含多个Block（线程块），而每个Block（线程块）中则有很多的thread（线程）。一个栅格中不同的Block通过不同的线程块索引（BlockIdx）来标识，同一个Block中的不同thread通过不同的线程索引（threadIdx）标识，这些索引只能通过核函数中由设备专用寄存器提供的只读型内建变量访问。这样，在核函数执行时每一个线程都有唯一的一个BlockIdx和一个threadIdx组合与之对应，在核函数中，通过这2个索引确定本线程的具体任务。

在建模过程中，首先在主机端进行预处理，找出网格模型的边界值，建立修正网格时所需的索引表并划分网格。将一个网格模型的修正任务分配到存在着若干个线程块的栅格中，线程块的具体规模由网格模型大小决定。每一个网格节点对应着线程块中的一个线程，其能够安全地访问采样数据并独立进行本线程多对应网格节点的修正。由于网格修正算法存在着丰富的数据并行性和任务并行性，因而在GPU上执行修正算法能够获得很大的性能提升。算法具体流程（见图4）如下：①读取原始数据；②分析原始数据，创建规则网格模型和索引表；③将原始数据和网格数据拷贝到设备存储器中；④启动核函数进行GPU加速，修正网格节点，同时中间变量存到设备内存的存储器中；⑤将结果从设备内存中拷贝到主机内存中；⑥划分三角形网格，剔除不合法的三角形；⑦通过OpenGL绘制网格模型。

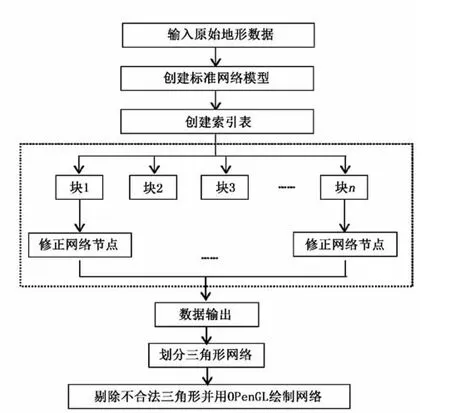
图4 算法主要流程图

5 试验结果与分析

在试验中，通过处理某工区地质体数据并对其进行建模以验证改进算法。该地质体数据为不规则数据，在程序中，对数据进行预处理后，建立了100×100的规则矩形网格模型，该网格模型单位矩形规格为95.157×116.994，直接三角形面片数为20000个。几何相似度采用对称Hausdorff距离进行评估，对称Hausdorff距离实际上是2个网格模型之间的最大误差，对称Hausdorff距离越小，2个网格模型之间的几何相似度越大。试验步骤分为3部分：①采用未优化的串行算法（简称CPU算法）进行处理、计算并绘制网格模型，记录程序建模所需时间；②采用优化后的CPU算法进行处理、计算并绘制网格模型，记录程序建模所需时间；③采用并行算法（简称GPU算法）进行处理、计算并绘制网格模型，记录程序建模所需时间。CPU串行算法和GPU算法程序运行数据对比表如表1所示。由表1可知，与一般串行建模算法相比，由于充分发掘建模算法的数据并行性和算法并行性，利用GPU强大的并行计算能力，使建模速度提高了50～60倍。

表1 CPU串行算法和GPU并行算法程序运行数据对比表

在建模精确度方面，虽然利用改进算法构建的网格模型与实际地形相比存在一定失真（见图5），但其失真度能够控制在很小范围内，因而能够满足常规地质建模要求。

图5 程序运行截图

6 结语

提出了一种针对不规则分布点的快速建模方法，该方法能够大幅提高建模速度，适用于复杂地质体的快速建模。该算法能够满足地质勘探中对大数据量网格快速建模的要求，充分体现了该算法在复杂地质体建模中的有效性。

［1］潘懋，方裕，屈洪刚.三维地质建模若干基本问题讨论 ［J］.地理与地理信息科学，2007，23（3）：75～78.

［2］余杰，吕品，郑昌文.Delaunay三角网构建方法比较研究 ［J］.中国图像图形学报，2010，15（8）：28～32.

［3］沅宁君，陈俊，于文茂，等.基于三维地震数据的并行希尔伯特黄算法研究 ［J］.计算机工程与设计，2012，32（6）：89～92.

［4］Jing Ming，Mao Pan，Honggang Qu，et al.GSIS：A 3Dgeological multi－body modeling system from netty cross－sections with topology ［J］.Computers ＆Geosciences，2010，36（6）：756～767.

［5］Hao Zhao，Runcai Bai，Guangwei Liu.3DModeling of Open Pit Based on AutoCAD and Application ［J］.Procedia Earth and Planetary Science，2011，3（1）：258～265.

［6］Wycisk P，Hubert T，Gossel W，et al.High－resolution 3Dspatial modelling of complex geological structures for an environmental risk assessment of abundant mining and industrial megasites ［J］.Computers ＆ Geosciences，2009，35（1）：165～182.

［7］David B K.大规模并行处理器编程实战 ［M］.赵开勇，汪朝辉，程亦超译.北京：清华大学出版社，2013.

［8］张舒，褚艳利.GPU高性能运算之CUDA ［M］.北京：中国水利水电出版社，2009.