长悬臂干挂石材支撑结构体系设计及其动力分析

杨明飞

（安徽理工大学土木建筑学院，安徽 淮南232001；合肥建工集团有限公司，安徽 合肥230088）

史雪梅

（安徽理工大学图书馆，安徽 淮南232001）

干挂石材装饰体系是融合了建筑艺术和功能艺术的一种新型结构体系［1～3］，基本组成包括支撑结构体系、石材和基础等，其特点是将多块石材悬挂在结构体系上，无需任何黏贴或灌浆等工艺，但是这种结构体系的受力分析至今还没有一个专门的设计规范对其进行指导，一般是借鉴一些相关规范作为参考［4，6］。为此，笔者以淮南市某广场项目为例，对长悬臂干挂石材支撑结构体系进行了设计，并对其进行了受力分析，以便为该类型结构的工程应用提供参考。

1 工程概况

该项目位于淮南市某广场，处于空旷地带，要求采用混凝土独立柔性基础，其上端留有预埋件，上部结构采用型钢结构进行承重，结构最大高度3.737m，厚度0.4m，两端悬挑长度均为8m，承受石材的重量为500kN，但是由于前后侧石材的厚度不同，对结构体系产生了一定的侧向弯矩。所有石材均采用纵横龙骨干挂的方式，钢材采用全焊透方式焊接为整体，要求设计的钢结构支撑体系满足竖向和水平向承载力和刚度要求。

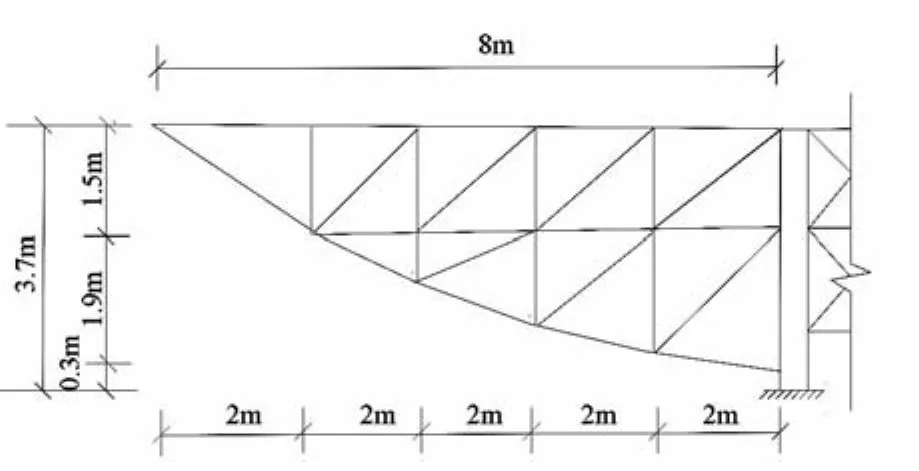
图1 结构设计方案图

2 支撑结构体系设计方案

通过对支撑结构体系进行概念设计，初步确定其设计方案。由三角形几何不变体系为基本框架进行扩展，同时为了干挂龙骨体系的建立，在结构中部水平位置增加了一根型钢梁，由于结构对称，取一半结构（见图1）。与基础连接的2根型钢柱采用350mm×350mm×12mm×19mm的H型钢制作。支撑结构体系其余钢材均采用36a＃槽钢。

3 数值模型

采用有限元软件ANSYS建立支撑结构体系数值模型（见图2）。其中，钢梁采用beam188单元进行模拟，所用钢材均为Q235，屈服强度205MPa，弹性模量为2.06×1011，密度取7850kg／m3。结构体系的2根H型钢柱固结于基础上表面。

图2 有限元模型

4 静力荷载分析

为了分析支撑结构体系的竖向承载能力，将石材的自重进行简化处理［7，8］。考虑结构承载以恒载为主，因此将竖向荷载（石材及钢材自重）乘以1.35的分项系数，对结构各节点进行均分，得出结构各节点的竖向受力约为25kN。同时为了考虑两侧石材厚度不等造成的侧向弯矩以及风荷载等侧向荷载作用，将支撑结构体系各节点的侧面施加0.2kN的侧向力，则竖向位移、侧向位移、第一主应力和Von Mises屈服应力的计算结果如图3所示。

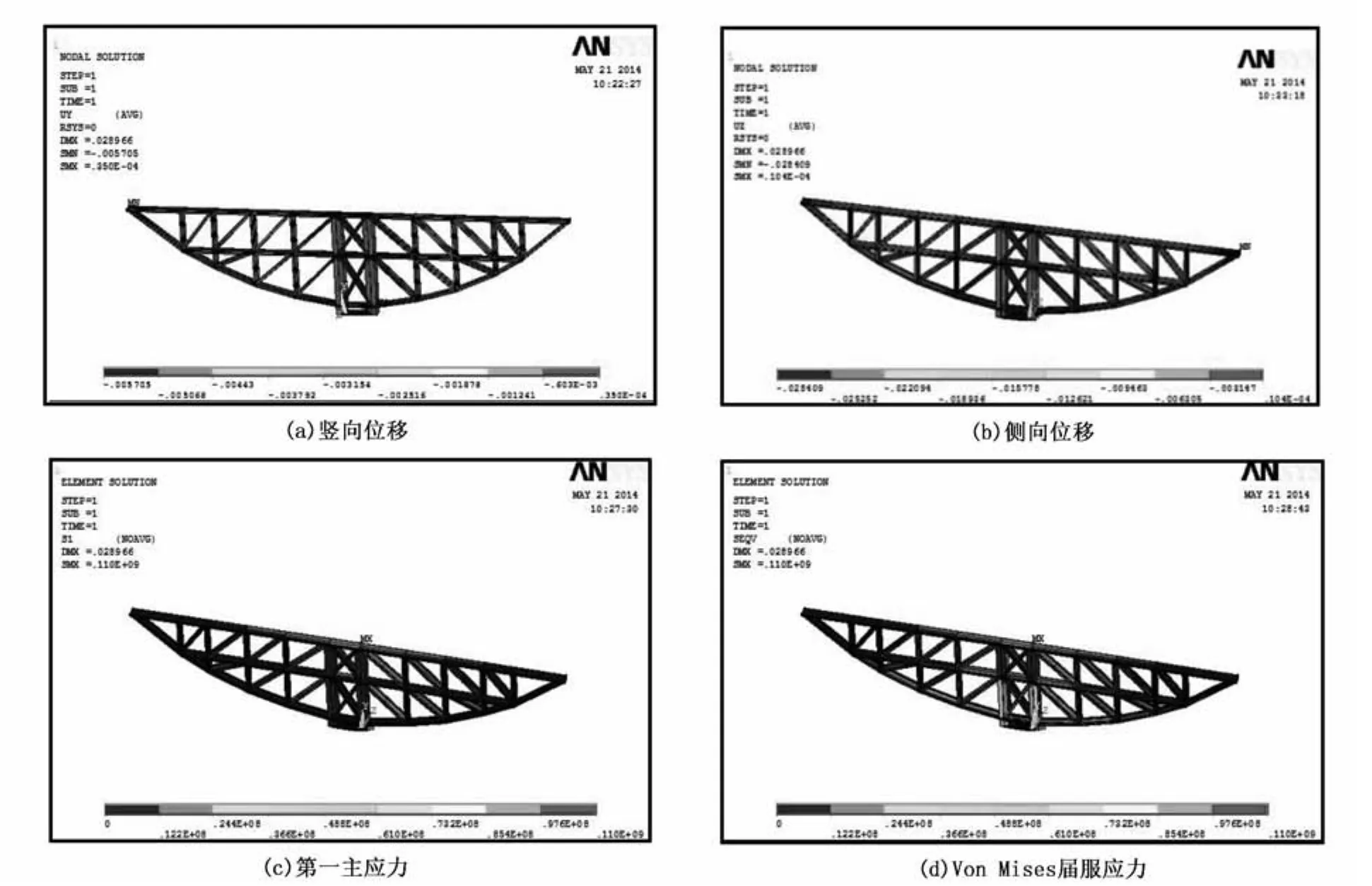
图3 结构体系数值计算结果

从图3（a）和图3（b）可以看出，支撑结构体系在竖向和水平荷载的作用下，在悬挑端竖向最大位移仅为0.0053m，同时侧向最大位移为0.0288m，说明在静力荷载作用下结构体系的刚度满足要求，不会对石材干挂的施工产生影响（设计中要求结构体系变形控制在0.06m以内）。由图3（c）和图3（d）可知，在竖向和水平静力荷载作用下，结构构件的第一主应力和Von Mises屈服应力最高达到110MPa，但是没有达到钢材的屈服强度205MPa。通过分析，对结构各构件的内力进行了提取，得到最大轴力为342kN，最大弯矩为170kN·m，最大剪力74kN，由此可以说明在静力荷载作用下结构体系的承载能力满足要求。

5 动力荷载分析

5.1 支撑结构体系自振特性分析

为了解干挂石材支撑结构体系的动力特性，首先对其进行了模态分析。模态分析是研究结构动力特性的一种有效方法和手段。模态是结构的固有振动特性，每一阶模态具有特定的固有频率、阻尼比和模态振型。模态分析的最终目标是识别出系统的模态参数，为结构系统的振动特性分析及优化设计提供依据。

支撑结构体系无阻尼自由振动方程如下：

式中，［M］和［K］分别是支撑结构体系的质量和刚度矩阵；分别是支撑结构体系各质点的加速度和速度列向量。

假设支撑结构体系做简谐振动，可以得到结构的广义特征值方程：

式中，ω是支撑结构体系的自振频率；｛Φ｝是支撑结构体系的阵型向量（n维）。方程（2）的特征行列式为：

求解之后可以得到支撑结构体系各阶的自振频率，其中最小的频率即为支撑结构体系的基频。

通过数值分析，得到了支撑结构体系各阶自振频率。表1列出了支撑结构体系的前10阶自振频率。由表1可知，对于支撑结构体系而言，随着模态阶数的增加，自振

频率逐渐增大。其自振以一、二阶频率（侧向水平振动）为主，在设计的过程中应予以注意。

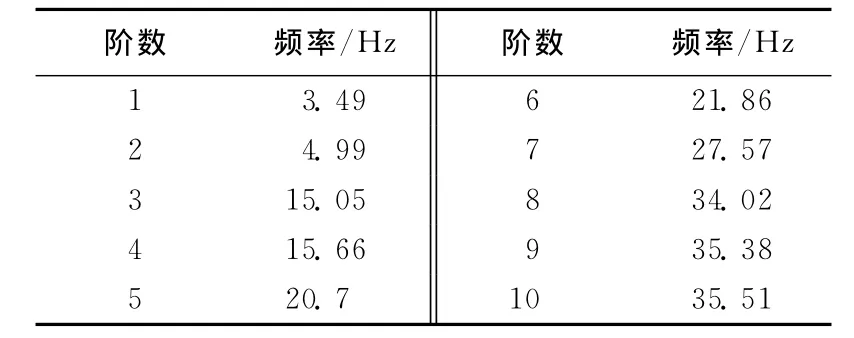
表1 支撑结构体系自振特性分析结果表

5.2 支撑结构体系动力分析

由于淮南地区为7度抗震设防区，针对该项目构件，选取了3条不同的地震波EL－Centro波、Taft波和人工波进行动力分析，其加速度幅值按照文献 ［9］的要求定为220gal，其波形图如图4所示。

由于干挂石材的支撑结构体系对加速度不作要求，因此仅列出竖向及侧向位移分析结果。其中，支撑结构体系的竖向位移结果基本和静力分析结果相同。在7度罕遇地震的作用下，结构体系的侧向位移在3种不同地震波作用的情况下分别为：在EL－Centro波作用下，侧向最大位移为0.0547m；在Taft波作用下，侧向最大位移为0.0558m；在人工波作用下，侧向最大位移为0.0556m（见图5）。

与静力荷载作用情况下相比，支撑结构体系的侧向位移将会增加。在EL－Centro波作用下，结构最大侧向位移增加了89.9%；在Taft波作用下，结构最大侧向位移增加了93.8%；在人工波作用下，结构最大侧向位移增加了93.1%。同时考虑到石材干挂施工时龙骨对于结构的加固作用，侧向最大位移会略有减少，由此可以说明在7度罕遇地震作用下，结构的侧向位移满足设计和施工要求。

6 工程验证

2014年初，工程施工基本结束。经现场测试发现，其竖向位移符合设计要求，最大侧向位移接近0.02m，与数值计算结果基本相符。

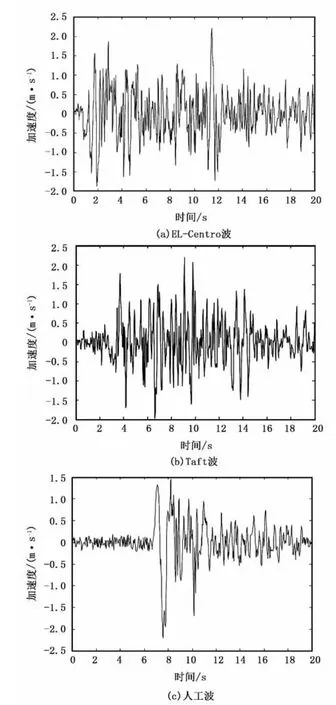
图4 结构输入用地震波

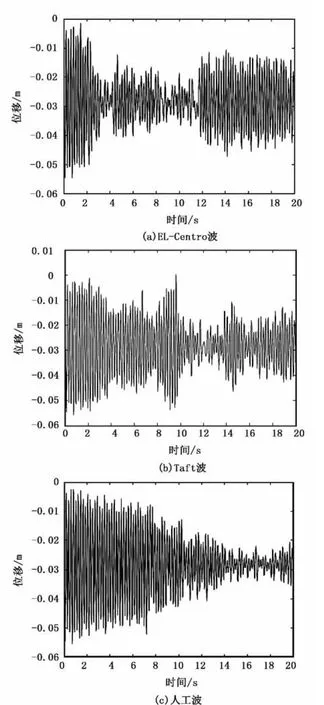
图5 不同地震波作用下结构体系的最大侧向位移时程响应图

7 结论与建议

7.1 结论

对结构体系进行竖向静力荷载作用下的受力分析，发现结构体系在竖向荷载作用下最大侧向位移为0.0288m，最大竖向位移为0.0053m，结构体系中构件的最大屈服应力为110MPa；在7度罕遇地震作用下对结构体系进行了动力分析，结构体系的竖向位移基本保持不变，而最大侧向位移出现增大，尤其在Taft波作用下，最大侧向位移达到0.0558m，相比静力荷载作用，其值增加了93.8%。综合分析认为，该项目结构体系的竖向和侧向承载力及刚度均满足设计和施工要求。

7.2 建议

干挂石材的支撑结构体系设计，在考虑经济性的前提下，尽量做到简洁，其中以三角形几何不变体系为基础进行扩展是一种较好的设计思路。此外，建议工程建成后定期对结构体系进行检测与维护。

［1］JC830.2－2005，干挂饰面石材及其金属挂件 ［S］.

［2］杜书廷.无框干挂石材灌注保温砂浆技术在某工程的应用 ［J］.建筑技术，2013，42（16）：75～78.

［3］高拥军.干挂石材幕墙采用现浇聚氨酯保温的探讨 ［J］.建筑节能，2009，37（2）：29～31.

［4］张旺春，杨秀美.背栓式叠型干挂石材幕墙的施工工艺与质量控制 ［J］.山东理工大学学报（自然科学版），2013，27（3）：75～78.

［5］李碧全.干挂石材幕墙工程的施工技术与质量控制 ［J］.建材发展导报，2011，9（4）：239～239.

［6］吴尉.石材幕墙连接技术 ［J］.施工技术，2010（S1）：547～551.

［7］卢华喜，梁平英，尚守平.外墙石材干挂结构的安全性评价与处理 ［J］.建筑技术，2009，40（5）：434～437.

［8］赵西安.对非花岗岩石材幕墙应用的若干建议 ［J］.建筑技术，2005，36（9）：648～651.

［9］GB50011－2010，建筑抗震设计规范 ［S］.