低辐射3G网络基站选址优化
张英杰 孙先佑 毛赐平 王镇道 许伟 汤龙波 艾朝阳
摘要:针对民众因担忧电磁辐射而投诉日益增多导致通信基站选址困难的现状,在考虑基站覆盖范围和建站成本的同时,兼顾基站电磁辐射对环境的影响,提出了面向低辐射的3G网络基站选址优化方案。通过对基站选址原则及其典型基站的电磁辐射模型分析,建立了基于多目标的基站评价模型,设计了基于改进的免疫优化算法3G网络基站选址优化方案,并以模拟实验区域为对象进行了仿真实验测试。实验结果表明:本文提出的选址优化方案不仅能以较小的基站建设代价满足信号覆盖要求,同时也降低了基站电磁辐射的影响,获得了更好的社会效益。
关键词:3G网络;通信基站;选址优化;电磁辐射
中图分类号:TP18 文献标识码:A
随着3G网络进入大规模商用阶段,为保证3G通信网络的通信质量,兴建了大量基站,同时也增加了基站周围环境的电磁辐射影响。基站选址的好坏直接决定了3G网络的信号质量和覆盖范围,且不合理的基站选址会导致严重的电磁辐射污染,同时基站的数量决定了基站的建站代价。因此面向低辐射的3G基站选址具有较强的理论意义并能应用于实际工程\[1-4\]。
国内外学者对3G基站的选址优化已做了大量研究:文献\[1\]基于遗传算法研究了WCDMA基站选址问题;文献\[2\]设计了一个基于网络控制和成本效率的最大无线覆盖网;文献\[3\]研究了多业务CDMA网络基站规划模型与算法;文献\[4\]研究了移动通信基站电磁辐射场强的建模与计算方法。这些优化方案从不同角度为基站选址优化工程提供了有益的思路,但3G网络基站选址是一个多目标优化问题,还须综合考虑覆盖率、电磁辐射污染与建站成本等要求。
13G网络基站选址优化模型
3G网络规划问题可以概括为在一定区域内,根据业务需要设计一个最优化的网络,即确定小区的数量和半径、每个基站的位置和参数,达到给定的业务目标和电磁辐射限值,并使建站成本最小化。3G基站选址问题是多目标优化问题,主要影响基站选址的因素包括传播环境、覆盖要求、建站代价和业务分布等\[5-8\]。本文在考虑最大化网络覆盖率的同时考虑了基站电磁辐射污染代价。即在达到要求覆盖率的同时如何保证良好的基站电磁辐射环境。鉴于此,本文运用免疫优化知识和数学建模方法将其抽象为多目标优化问题,以解决3G网络基站的选址优化问题。
1。13G网络基站选址优化的原则
基站站址选取合适与否对网络性能和成本有很大影响,不合适的站址选择不仅会导致某些地方出现覆盖盲区,甚至会造成电磁辐射污染。因此,3G网络基站的选址,应遵循以下原则[9]。
1)基站规划首先须考虑基站电磁辐射对公众健康及周围环境的影响。不同类型的基站天线,电磁辐射情况也不相同。通过计算基站天线电磁场值的大小和分布情况,从而确定站址是否符合辐射标准。
2)站址规划应尽量保证3G网络的布点接近理想蜂窝网络结构。标准的蜂窝网络能保证信号均匀分布在覆盖区内,减少电磁污染,并能避免频繁的基带切换和弱信号区。
3)基站选址要尽可能考虑站址分布和网络业务量的要求,网络业务与基站分布应基本相同,并优先考虑热点地区业务量要求。
1。2基站电磁辐射环境估算模式
影响电磁辐射污染代价的主要因素有两个:一是信号接收点电磁辐射功率,二是基站的电磁辐射频率。只有当这两个因素超过允许限值时,才会对环境造成电磁污染的影响。根据电磁辐射标准和规定,移动通信基站频率为30~3 000 MHz,该频段对应功率密度导出限值为0。4 W/m2(40 μW/cm2),即 公 众 照 射导出限值为40 μW/cm2。以单个基站管理目标值选取功率密度的1/5作为标准,即以80 μW/cm2作为公众照射导出限值\[4,10\]。
根据电磁辐射环境影响评价方法与标准\[4\],可知远场轴向功率密度公式为:
ρ=100PG4πr2。(1)
式中:ρ为远场轴向功率密度(单位:μW/cm2);P为发射机净功率(单位:W);G为天线增益(单位:倍数),G=10G/10;r为测试点与天线轴向的直线距离(单位:m)。
发射天线的净功率为:
10lgP=10lgPr-Lr-Lc。(2)。
式中:Pr为发射机的发射功率(单位:W);Lr为馈线损耗;Lc为系统组合损耗。
为便于比较,选取一般情况下的3G网络基站运行参数,发射功率为20 W,馈线损耗为3 dB,实际发射天线增益15 dB,系统组合器损耗4 dB,由远场轴向功率密度公式,可计算得到不同r值对应的远场轴向功率密度如表1所示。
由表1可知,当远场轴向距离为28 m时,功率已到0。08 W/m2,低于电磁辐射对人体影响的限值。
表1不同r值对应测试点功率密度
Tab。1The different r values of power density
测试点距离
/m
远场轴向功率密度
/(μW·cm-2)
10
70。92
20
17。11
30
7。60
40
4。28
50
1。90
1。3基站选址优化的数学模型
3G基站的优化选址是在满足约束条件情况下选择最优化结果,是一个多目标组合优化问题。在基站规划阶段,由于无法实际测量网络覆盖率和电磁辐射率,可以通过计算测试点与基站之间的链路损耗来衡量覆盖率,通过计算测试点轴向功率密度计算电磁辐射率的污染情况,并通过计算选用基站的个数来计算建站成本。
在本文实验中,设定候选基站个数集为B={1,2,…,n},n表示候选站点个数;模拟测试点集为T={1,2,…,m},m表示测试点个数。根据3G网络选址的特点,计算覆盖率、电磁辐射污染率以及建站成本的函数如下。
1)基站选址中覆盖率的目标函数,即基站覆盖测试点的个数/测试点总数目。假设测试点s(s∈T)从候选基站k(k∈B)接收的信号强度大于阈值Q,则可认为测试点s被基站k覆盖。测试点s被基站覆盖的情况表示为:
xs=1,P-εdsk≥Q;0,P-εdsk 式中:P为基站的发射功率;ε为功率损耗系数;dsk为测试点s与候选基站k之间的距离。则测试点覆盖率函数为: f1=∑ms=1xsm。(4) 2)为便于计算,把电磁辐射污染率转化为求没有受到电磁辐射污染的测试点比例。即没有受电磁辐射污染的测试点个数/测试点总数目。若测试点接收到的轴向功率ρ<0。08 W/m2,即认为该测试点没有受电磁辐射污染。设测试点s的电磁辐射情况为: gs=1,ρ<0。08;0,ρ≥0。08。(5) 式中:ρ为远场轴向功率密度。测试点没有受电磁辐射污染的函数为: f2=∑ms=1gsm。(6) 3)基站的建站成本用选用基站的数目表示,且设定单个基站的建站成本相同。为使建站成本函数与覆盖率、电磁辐射率一致,将其转为求最大值,因此建站成本函数可表示为: f3=n-n0n。(7) 式中:n为总的基站个数;n0为选用基站个数。 2基于免疫计算的3G基站选址算法 2。1抗体编码及种群初始化 在免疫优化算法(IOA)中\[11\],将待解问题作为抗原,问题的解作为抗体。在基站选址规划中,候选基站只有选中与没被选中2种情况,因此本文采用二进制的编码方式,每个抗体对应一种基站选址的解,基因座的值为对应候选站址的选择情况。抗体编码记为A=(a1,a2,…,an),其中ak为对应第k(k∈B)个站址被选择的情况,B为候选站址数集,即 ak=1,k被选中;0,k没被选中。(8) 免疫算法初次运行须生成一个初始种群,一般用随机方法生产初始种群。但这种方法生成的初始种群解不稳定、随机性大,不能保证种群的多样性,也不能有效利用解空间信息,从而会限制算法的求解效率和寻优空间。因此本文采用如下方式产生初始种群:第1次运行算法时,采用随机的方法产生抗体种群;再次运行算法时,采用从上次产生的抗体中抽取已有的优秀解作为潜在的较好解,补充30%到初始种群中,余下的70%用随机方式产生。这样,既保证种群多样性,又能提高算法收敛速度。 2。2抗体亲和度评价函数 为同时考虑电磁辐射污染代价、测试点覆盖率和建站成本对基站选址的影响,本文采用权重法把3个目标的问题转化为单目标问题,抗体亲和度评价函数为: f(A)=αf1+βf2+γf3。(9) 式中:α为测试点覆盖率的权重系数;β为基站电磁污染代价权重系数;γ为基站建站成本的权重系数;且α+β+γ=1。该评价函数的值f(A)∈[0,1],f(A)的值越大,表明该选址方案越好。 2。3抗体浓度 由于本文采用二进制编码方案,抗体编码表示候选基站是否被选中,两个抗体的差异性表示2种方案站址选择情况的差异,因此本文把抗体编码中解的差异值表示为抗体的距离,其计算公式为: D(A(x),A(y))=∑ns=1xs-ys。(10) 当抗体距离D(A(x),A(y))小于阈值θ时,为相邻抗体,如式(11)所示: L(A(x),A(y))=1,D(A(x),A(y))<θ;0,其他。(11) 抗体A(x)的浓度指抗体种群中的相邻数目与种群数量大小的比值,其计算公式为: Density(A(x))=∑ns=1(A(x),A(y))n。(12) 其中n为抗体种群规模大小。 2。4算子设计 本文算法采用抗体浓度抑制、克隆变异和精英交叉3个算子: 抗体浓度抑制:计算每代抗体及克隆副本的浓度。选取浓度较低的l个抗体和随机产生的n-l个抗体共同组成下一代种群,抗体浓度抑制能较好地防止种群早熟收敛。 克隆变异:克隆记忆库种群中的抗体,其规模为E,并以概率pr变异每个克隆副本,规模E的计算公式为: E=round(λf(A)Density(A)∑CMk=1f(A))。(13) 式中:λ为克隆系数;抗体A的浓度为Density(A);抗体A的亲和度函数值为f(A);∑CMk=1f(A)为克隆母体种群的抗体亲和度值之和;CM为克隆母体的种群规模;round()表示取整函数。 精英交叉:用种群中的每个抗体与精英个体以给定的概率pe进行交叉,以提高收敛速度,并改善种群结构\[12\]。 2。5算法基本框架 本文设计的算法基本框架如下。 步骤1输入抗体种群规模P,记忆库种群规模S,克隆母体种群规模T; 步骤2初始化抗体种群。若首次运行本文算法,则随机产生P个抗体组成抗体种群A(0);否则,若第t次运行,则把上次记忆库中的l个优秀抗体和随机产生的(P-l)个抗体组成新的抗体种群A(t); 步骤3从初始化种群A(0)中选取亲和度较优的前T个抗体组成克隆母体种群A(T),并以概率pr对克隆母体种群按克隆变异进行操作,得到克隆种群A(C); 步骤4将精英个体E与种群A(T)∪A(C)按照概率pe进行交叉操作,得到新的种群A(S); 步骤5将种群A(S)中抗体的亲和度值以降序排列,用亲和度高的抗体替换记忆库种群A(l)中的部分抗体; 步骤6对种群A(T)∪A(C)实施抗体浓度抑制操作,生成下一代种群; 步骤7若结果满足终止条件,则输出种群中亲和度最优的抗体,算法结束;否则转到步骤3。
3仿真实验与结果分析
3。1免疫优化算法性能测试
为验证本文改进算法的稳定性和有效性,本文选用文献\[13\]中列出的16个典型函数对算法进行检验。并与文献\[13\]中的云遗传算法(CGA)和文献\[14\]中的混沌云克隆算法(CCCSA)结果进行比较。
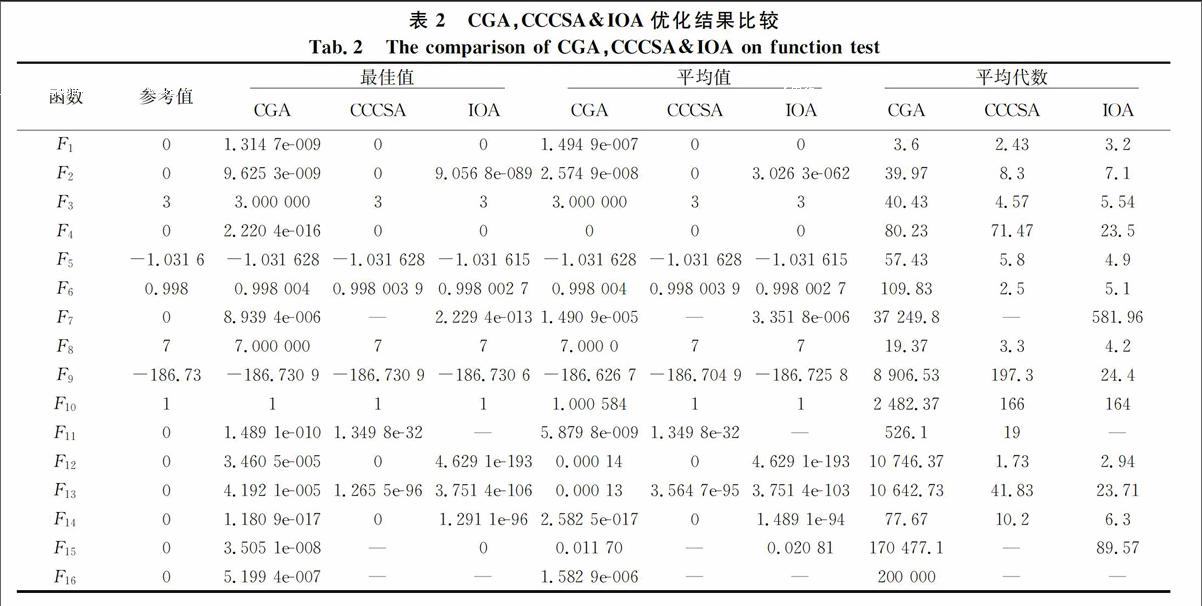
实验参数按文献\[13\]和文献\[14\]设置如下:种群大小均为100,最大迭代次数均为1 000次,测试函数均独立运行30次。其中,CGA数据来自文献\[13\],CCCSA数据来自文献\[14\]。实验结果如表2所示。
表2CGA,CCCSA&IOA优化结果比较
Tab。2The comparison of CGA,CCCSA&IOA on function test
函数
参考值
最佳值
平均值
平均代数
CGA
CCCSA
IOA
CGA
CCCSA
IOA
CGA
CCCSA
IOA
F1
0
1。314 7e009
0
0
1。494 9e007
0
0
3。6
2。43
3。2
F2
0
9。625 3e009
0
9。056 8e089
2。574 9e008
0
3。026 3e062
39。97
8。3
7。1
F3
3
3。000 000
3
3
3。000 000
3
3
40。43
4。57
5。54
F4
0
2。220 4e016
0
0
0
0
0
80。23
71。47
23。5
F5
-1。031 6
-1。031 628
-1。031 628
-1。031 615
-1。031 628
-1。031 628
-1。031 615
57。43
5。8
4。9
F6
0。998
0。998 004
0。998 003 9
0。998 002 7
0。998 004
0。998 003 9
0。998 002 7
109。83
2。5
5。1
F7
0
8。939 4e006
—
2。229 4e013
1。490 9e005
—
3。351 8e006
37 249。8
—
581。96
F8
7
7。000 000
7
7
7。000 0
7
7
19。37
3。3
4。2
F9
-186。73
-186。730 9
-186。730 9
-186。730 6
-186。626 7
-186。704 9
-186。725 8
8 906。53
197。3
24。4
F10
1
1
1
1
1。000 584
1
1
2 482。37
166
164
F11
0
1。489 1e010
1。349 8e32
—
5。879 8e009
1。349 8e32
—
526。1
19
—
F12
0
3。460 5e005
0
4。629 1e193
0。000 14
0
4。629 1e193
10 746。37
1。73
2。94
F13
0
4。192 1e005
1。265 5e96
3。751 4e106
0。000 13
3。564 7e95
3。751 4e103
10 642。73
41。83
23。71
F14
0
1。180 9e017
0
1。291 1e96
2。582 5e017
0
1。489 1e94
77。67
10。2
6。3
F15
0
3。505 1e008
—
0
0。011 70
—
0。020 81
170 477。1
—
89。57
F16
0
5。199 4e007
—
—
1。582 9e006
—
—
200 000
—
—
表2中,参考值为函数的理论最小值,平均代数为参考适应度值与最佳适应度值差的绝对值小于10-3时,函数多次独立实验的平均值,‘—表示其在1 000次迭代后部分最优值和参考值的绝对差值大于10-3,所以未把其平均代数进行比较。
IOA利用了基于克隆变异的种群进化机制,能较好地继承父代优秀抗体。抗体浓度抑制防止了种群的早熟收敛,从而有效防止了算法陷入局部最优值;精英交叉策略提高了算法的收敛速度,改善了群体结构。由表2可知,除F11和F16这样的高维、变量范围比较大的函数外,IOA对其余函数的最优值、平均值和平均代数均优于CGA;综合算法精度和收敛速度,IOA的整体性能优于CCCSA。
为进一步验证算法的有效性,本文选取2个典型多峰值函数进行测试,并给出了算法亲和度变化图。
实验参数设置如下:初始种群规模N=100,有效判定阈值C=round(c/4),最大进化代数G=100,误差控制E=0。082。图1为Multi函数进化代数与算法亲和度之间的变化曲线;图2为Schaffer函数进化代数与算法亲和度之间的变化曲线。由图1和图2可知,两个函数的最优亲和度值都等于或近于1,说明本算法具有较强的全局搜素能力。
Multi函数为:
f1(x,y)=xsin(4πx)-ysin(4πy+π);
x,y∈[-2,2]。(14)
Schaffer函数为:
f2(x,y)=0。5-sin2(x2+y2)-0。51+0。001(x2+y2);
x,y∈[-10,10]。(15)
3。2基站选址仿真实验与分析
基站选址仿真实验在Windows7(32位)系统,Pentium(R处理器),2。7 GHz主频,2 GB存储器,仿真软件Matlab R2011a的机器上运行20次。
进化代数
实验选择与文献\[1\]相同的数据和环境:选取一个20 km×20 km平坦的实验区域,设该区域的基站候选站址集为B={1,2,…,60},信号测试点集为T={1,2,…,128},并假定每个基站的发射功率相同且为定值,每个测试点没被基站覆盖所产生的损失相同,每个候选站址的建站代价相同,建站目标为:最小化的电磁污染率,最大化网络覆盖率,最小建站成本;测试点分布及基站候选站址如图3所示。
两种算法的种群规模P=100,抗体都采用二进制编码,最大进化代数均为Gm=200,编码长度D=60,抗体初始化概率均为0。8,交叉概率均为0。6,变异概率pr=0。6,抗体间的距离阈值θ=30,记忆库种群规模S=30,克隆母体种群规模T=60,克隆系数a=10。基于实际建站经验值,目标函数f1的权重系数α=0。4,目标函数f2的权重系数β=0。4,目标函数f3的权重系数γ=0。2。
x/km
图3测试点即候选站址分布
Fig。3Candidate sites and test points
of distribution
图4为本文算法与文献\[1\]算法亲和度函数值的比较。从图4可以看出,随着进化代数增加,算法的平均亲和度值也逐渐增加,且本文算法平均亲和度值优于文献\[1\]算法。
进化代数
图4 两种算法亲和度随进化代数的比较
Fig。4Affinity compare the two algorithms
反映选址优化方案性价比的另一个指标是测试点覆盖率与基站数目的比,比值越大,说明选址优化方案的性价比越高。两种算法的测试点覆盖率和基站数目的比值如图5所示。
进化代数
图5两种算法测试点覆盖率与基站数目比值
Fig。5Test point coverage ratio and the
number of base stations
图6表示基站个数随进化代数的变化,从图6可以看出,本文选址方案的平均建站数目明显少于文献\[1\],表明本文算法的建站代价较小。这主要因为本文算法采用的精英交叉策略扩大了算法的寻优空间以及种群的多样性。
从图7可以看出,随着进化代数的增加,本文的测试点电磁辐射率小于极值的比例随着进化代数的增加而变大,说明本文算法具有较强的寻优能力,可以用较少的基站和较低的电磁污染率获得较高的信号覆盖率,减少基站电磁辐射污染。
进化代数
图6基站个数随进化代数的变化
Fig。6 Number of base changes in Algebra
进化代数
图7本文算法电磁辐射率随进化代数的变化
Fig。7Algorithm electromagnetic radiation increaseswith
evolutionary changes Algebra
4结束语
3G网络规划的重点和难点是怎样降低建站成本、电磁辐射率和保证覆盖率。本文分析了3G网络基站选址的主要目标及基站选址优化的数学模型等问题,为下一步低能耗、环保型基站的建设提供参考。在仿真实验环境下,与文献\[1\]的算法进行了对比,结果表明,本文算法优于文献\[1\]中算法,能够提供科学合理的绿色网络基站规划方案,降低了3G网络的建站成本和电磁辐射率。
参考文献
[1]MUNYANEZA J,KURIEN A。Optimization of antenna placement in 3G networks using genetic placement algorithms\[J\]。Communication & Information Technology,2009,36(3):70-80。
\[2\]KILINC D, OZGER M, AKAN O B。 On the maximum coverage area of wireless networked control systems with maximum costefficiency under convergence constraint\[J\]。Automatic Control,2014,77(10):1-6。
\[3\]施永贵, 王洪峰, 唐加福, 等。 多业务 CDMA 网络基站规划模型与算法研究\[J\]。 系统仿真学报, 2013, 25(6): 1410-1414。
SHI Yonggui, WANG Hongfeng, TANG Jiafu,et al。Research on model and algorithm for multiservice CDMA network base station planning\[J\]。 Journal of System Simulation, 2013, 25(6): 1410-1414。(In Chinese)
\[4\]陈习权,孙杰。通信基站电磁辐射场强的系统建模与数值仿真\[J\]。电波科学学报,2013,28(1):183-188。
CHEN Xiquan,SUN Jie。Systemic modeling and numerical simulation of electromagnetic radiation field intensity around mobile communication base stations\[J\]。Journal of Radio Science,2013, 28(1): 183-188。 (In Chinese)
\[5\]LAKSHMINARASIMMAN N。Base station placement for dynamic traffic load using evolutionary algorithms\[J\]。 Wireless Personal Communications,2013,72(1):225-231。
\[6\]朱思峰,刘芳,柴争义。基于免疫计算的WCDMA网络基站选址优化\[J\]。电子与信息学报, 2011, 33(6): 1492-1495。
ZHU Sifeng, LIU Fang, CHAI Zhengyi。 A novel immune algorithm for WCDMA base station locations optimization[J]。 Journal of Electronics & Information Technology, 2011,33(6):1492-1495。(In Chinese)
\[7\]唐朝伟,李小龙,邵艳清,等。基于分层多目标优化算法的无线网络规划\[J\]。计算机工程,2010, 36(9):7-9。
TANG Chaowei,LI Xiaolong,SHAO Yanqing,et al。 Wireless network planning based on hierarchical multiobjective optimization algorithm\[J\]。Computer Engineering,2010, 36(9): 7-9。 (In Chinese)
\[8\]张英杰,毛赐平,俎云霄,等。基于免疫算法的 TDSCDMA 网络基站选址优化\[J\]。通信学报, 2014,35(5): 44-48。
ZHANG Yingjie,MAO Ciping,ZU Yunxiao,et al。Immune algorithmbased base station location optimization in the TDSCDMA network\[J\]。Journal on Communications,2014, 35(5): 44-48。 (In Chinese)
\[9\]GONZLEZBREVIS P,GONDZIO J,FAN Y,et al。 Base station location optimization for minimal energy consumption in wireless networks\[C\]//Vehicular Technology Conference (VTC Spring), 2011 IEEE 73rd。 IEEE, 2011: 1-5。
\[10\]LIU J,TING S W,SARKAR T K。Basestation antenna modeling for fullwave electromagnetic simulation\[C\]//Antennas and Propagation Society International Symposium (APSURSI)。IEEE, 2014: 2106-2107。
\[11\]ALONSO F R, OLIVEIRA D Q, ZAMBRONIDESOUZA A C。 Artificial immune systems optimization approach for multiobjective distribution system reconfiguration\[J\]。 IEEE Transactions on Power Systems,2015,30(2):840-847。
\[12\]慕彩红,焦李成,刘逸。M精英协同进化数值优化算法\[J\]。软件学报,2009,20(11):2925-2938。
MU Caihong,JIAO Licheng,LIU Yi。Melite coevolutionary algorithm for numerical optimization\[J\]。Journal of Software, 2009, 20(11): 2925-2938。 (In Chinese)
\[13\]戴朝华,朱云芳,陈维荣,等。云遗传算法及其应用\[J\]。电子学报,2007,35(7):1419-1424。
DAI Chaohua,ZHU Yunfang,CHEN Weirong,et al。Cloud model based genetic algorithm and its applications\[J\]。Acta Electronica Sinica, 2007, 35(7): 1419-1424。 (In Chinese)
\[14\]张英杰,赵芳芳。混沌云克隆选择算法及其应用\[J\]。湖南大学学报:自然科学版,2014,41(3): 101-106。
ZHANG Yingjie,ZHAO Fangfang。Chaos cloud clonal selection algorithm and its application\[J\]。Journal of Hunan University:Natural Sciences,2014, 41(3): 101-106。 (In Chinese)

