凸轮磨削的仿形跟踪误差补偿

隋 振，李 聪，王 静

(吉林大学通信工程学院，长春130022)

凸轮磨削的仿形跟踪误差补偿

隋 振，李 聪，王 静

(吉林大学通信工程学院，长春130022)

为提高凸轮磨削的加工精度，减小凸轮的轮廓误差，并进一步提高磨削系统的鲁棒性，采用了新的误差补偿方法-仿形跟踪误差补偿，将实际的仿形跟踪误差值补偿到X轴的给定数值序列。运用Matlab搭建了两轴联动反馈系统，并设计模糊PID(Proportional-Integral-Derivative)控制器以实现对系统的在线补偿。采用一种形状较难加工的凸轮片作为实验对象验证补偿效果和控制器的性能。仿真实验结果表明，该方法不仅能有效减小凸轮的轮廓误差，简化了计算过程，并且使系统的响应速度加快，与传统PID控制器相比还具有较好的鲁棒性。

仿形跟踪误差补偿;凸轮磨削;模糊PID;鲁棒性

0 引 言

凸轮作为各种自动化机械中广泛应用的零部件，对实现复杂的运动起到了至关重要的作用。目前多运用加工中心及专用凸轮磨床加工凸轮零部件，其加工过程涉及到工件旋转轴C轴和砂轮进给轴X轴的两轴配合问题，两个运动轴在加工过程中难免会各自产生误差，每个运动轴上产生的微小误差累积到凸轮轮廓上就会产生较大的轮廓误差。

为此，提高加工精度的一种方法是提高每个运动轴的跟踪精度，力求每个运动轴都具有良好的快速动态跟踪性能。文献［1］在这一思想基础上提出了一种跟踪控制器，它集零相位误差跟踪控制及干扰观测器于一身，以每个轴的精度为出发点，利用逐个提高各运动轴的跟踪精度满足加工精度。另一种方法是提高两运动轴的配合精度，该方法在一定程度上可以忽略单轴的跟踪误差，只要两个运动轴实现同步，即可提供较高的加工精度。传统方法是由Koren［2］首先发表的交叉耦合控制算法(CCC:Cross-Coupled Control)，文献［3-5］依据这种策略对交叉耦合进行了进一步的探讨与应用，其思想是由各运动轴的速度误差推导出轮廓误差，再将经各种补偿方案以及补偿算法计算出的补偿量分配到各个运动轴。文献［6］将变增益交叉耦合控制算法应用于精密机床，其特点是在保证位置环结构和参数不变的前提下，提高机床的加工精度。文献［7］提出了一种位置误差控制器联合模糊进给调节器的整体方案，其位置误差控制部分是一种改进的CCC控制器，该方案虽然有效地提高了加工精度，但大大增加了系统的复杂程度，实现成本较高。文献［8］同时运用CCC与模型参考自适应算法，通过实时估计误差信息，针对进给量进行实时的修正，从而提高凸轮的加工精度。笔者基于仿形跟踪误差补偿方法设计了模糊控制器，仿真实验表明，该方案能有效地提高轮廓加工精度，并能提高系统的鲁棒性。

1 仿形跟踪误差补偿结构及模型

实际凸轮磨床系统中，C轴作为系统的主导轴，X轴作为从动轴，X轴对C轴的跟踪一般有两种方式:一是X轴跟踪C轴输入的理论值;二是X轴跟踪C轴的实际输出值。这两种跟踪方式针对不同的系统及不同的工件各有优点。凸轮的加工精度主要受X轴对C轴实际输出的跟踪精度影响，其跟踪误差越小，凸轮的加工精度越高。因此如何提高X轴对C轴实际输出的跟踪精度，努力实现两运动轴的良好配合则成为提高其加工精度的关键。笔者定义了仿形跟踪误差，即砂轮中心点实际坐标与砂轮中心点应处坐标值之差，提出仿形跟踪误差补偿，结合两种跟踪方式，结构上利用X轴跟踪C轴输入的理论值，同时将X轴的仿形跟踪误差反馈到X轴的输入序列，从而提高从动轴X轴对主导轴C轴实际值的跟踪精度。该名称来源于其工作特点类似于仿形加工中刀具的运动轨迹是未知的，通过测量设备实时测量模具获得，而该系统中X轴实际跟踪的曲线也是由理论值和C轴实际运行情况共同决定的(见图1)。由于模糊PID控制器可根据不同工况对自身的3个参数进行实时调整，从而提高系统的鲁棒性，因此，利用其作为仿形跟踪误差补偿器。此外，工件旋转的速度同样是影响凸轮加工精度的重要因素，笔者采用的仿形跟踪误差补偿是从补偿的角度考虑问题，为了验证补偿的效果，需要在恒转速实验条件基础上进行。

图1 仿形跟踪误差补偿框图Fig.1 The diagram of profiling tracking error compensation

图2 仿形跟踪误差模型示意图Fig.2 The diagram of profiling tracking errormodel

由于运动轴各自会存在滞后，C轴和X轴的输出都不能完全跟踪给定值，然而一旦凸轮轮廓确定，便可根据其升程表得到砂轮中心点X关于工件旋转轴旋转角度C的函数X(C)，该函数仅由凸轮的形状决定。因此即便两轴的跟踪性能不让人满意，只要砂轮中心点的实际位置X能跟踪C轴的实际旋转角度对应的X(C)函数值，就能实现两个运动轴的良好配合。而两运动轴的运动状况可以体现凸轮的轮廓误差，因此将两运动轴的状态绘制成类似于升程曲线的图像(见图2)。

图2中实线是两运动轴的理论运动曲线，虚线是系统实际工作对应的运动曲线，e是仿形跟踪误差。

由公式

可知，通过减小仿形跟踪误差，能减小轮廓误差。ε为轮廓误差，k是仿形跟踪误差和凸轮轮廓误差之间的相关系数，其绝对值不大于1。θi是某时刻C轴实际的旋转角度，Xi是凸轮在这一角度时砂轮中心点的理论位置，X'i是该时刻砂轮中心点的实际位置。

2 模糊PID控制器设计

模糊控制理论作为智能控制领域中的重要成员，其主要思想是将定量问题模糊化后，经过相应的逻辑推理，再将推理得到的结论经过解模糊器定量输出，从而实现令人满意的控制效果。模糊控制与传统控制方式相比具有对被控对象数学模型的精确性要求不高、控制方法易于掌握、有较好的鲁棒性等优点［9］。

应用于本文的模糊控制原理如图3所示。

图3 模糊PID控制器在凸轮磨削系统中的应用Fig.3 The fuzzy PID controller using in cam grinding system

由图3可知，将量化后的仿形跟踪误差及仿形跟踪误差的变化率作为模糊控制器的输入，再经过模糊器、模糊推理机、解模糊器、输出量化因子，最后输出3个参数的增量，从而实现在线整定，以满足控制器在不同工况下的要求。PID(Proportional-Integral-Derivative)控制器的初始值可由实验确定一组效果较理想的组合

2．1 输入量和输出量的变化区间

为体现补偿方式结合模糊控制器的控制效果，笔者采用如图4所示的凸轮片作为实验对象，由于这种凸轮形状不对称，且表面部分凹陷，因此加工难度较高。

找到所确定的输入量和输出量变化的区间，这是系统实际的范围，然后为了将这些区间量化到合适的离散区间，因此需要设计比例因子和量化因子［11］。利用Matlab-Simulink进行实验，通过实验的方法得出仿形跟踪误差e及其变化率ec在简单闭环控制下的变化范围。为验证鲁棒性，于C轴转角为200°时，与C轴加入阶跃扰动，实验设置C轴的转速10°/s。

模糊控制器输入和输出的模糊子集论域分别为

图4 凸轮形状示意图Fig.4 The diagram of cam

图5，图6分别为简单闭环控制下仿形跟踪误差和误差变化率的变化范围。从图5和图6可看出，仿形跟踪误差e的范围是(-0.01，0.01)，仿形跟踪误差变化率ec的取值范围是(-0.5，0.4)，两个输入的论域都可确定为(-3，-2，-1，0，1，2，3)。由此确定实验系统中输入的量化因子。

图5 简单闭环控制下仿形跟踪误差变化范围Fig.5 The profiling tracking error rangewith the simple closed loop control

图6 简单闭环控制下仿形跟踪 误差变化率的变化范围Fig.6 The range of profiling tracking loop control error variety-rate with the simple closed

为确定输出量的变化区间，分别针对PID3个参数进行试验，确定其变化范围。先确定比例系数Kp的取值范围，图7是取不同比例系数情况下系统的仿形跟踪误差。图8为不同积分系数下的仿形跟踪误差。

图7 不同比例系数下的仿形跟踪误差Fig.7 Profiling tracking error under different proportional coefficients

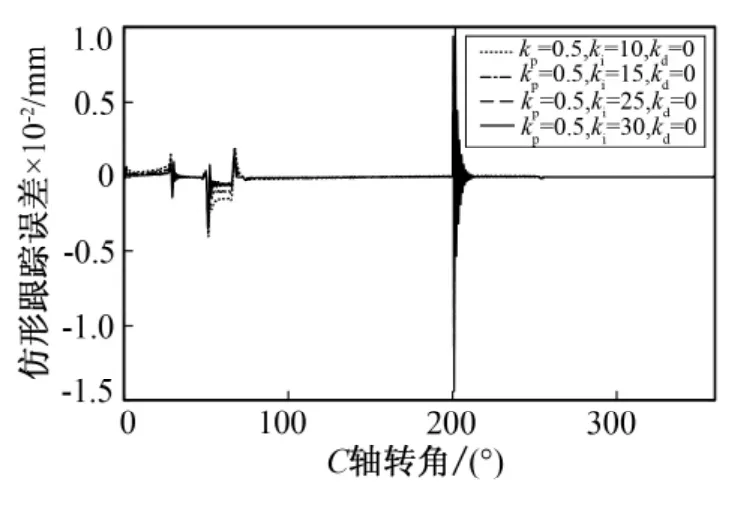
图8 不同积分系数下的仿形跟踪误差Fig.8 Profiling tracking error under different integral coefficients

从图7可以看出，随着Kp的增大，稳态误差会相应减小，但动态过程会延长，可确定Kp的范围为(0，1．5)，根据经验，初始值K'p可确定为0．5。

图9为不同微分系数下的仿形跟踪误差。由图9可以看出，Kd大于0．3时，仿形跟踪误差会增加，在扰动作用下会产生激烈的振荡，因此可以确定微分系数的范围(0，0．3)，取初始值K'd=0．1。因而将Gkp，Gki，Gkd分别取1。

模糊器采用三角形隶属度函数，其函数图形由图10所示。

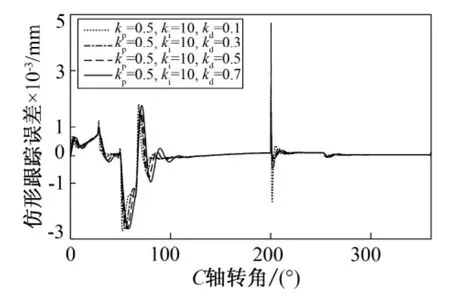
图9 不同微分系数下的仿形跟踪误差Fig.9 Profiling tracking error under different differential coefficients

图10 三角形隶属度函数Fig.10 Triangularmembership function

2．3 语言变量和隶属度函数的确定

针对这一步骤，首先应确定语言变量，再确定语言变量的模糊值，最后挑选其隶属度函数。对本系统，语言变量确定为仿形跟踪误差e及仿形跟踪误差变化率ec，语言变量值取NB，NM，NS，ZO，PS，PM，PB 7个模糊值;输出语言变量为Δkp、Δki、Δkd，语言变量值也取NB，NM，NS，ZO，PS，PM，PB 7个模糊值［10］。

模糊器为模糊推理环节提供输入，笔者运用三角形模糊器，三角形隶属函数运算较简单，对系统要求不高，并具有较好的性能，所以适合用于在线调整。

2.4 模糊规则的编译

编译模糊规则是比较困难的一步，每条规则都会影响到系统的输出。此外模糊规则主要来源于实际经验，所以，要求对系统的实际情况相当了解。在不断地调试规则后得到最理想的输出性能，才算是确定了最佳的模糊规则［12］。

PID控制规律为

控制输出由以下3部分组成［11，12］。

比例环节。其值的大小决定了系统的响应速度和精度，但一味地追求过高的速度可能会导致系统不稳定。需根据实际的工作状况选择合适的大小。

积分环节。根据系统的历史状态实现消除系统的稳态误差的目的。其作用的强弱取决于KI的大小，与KP相似，倘若其值过大，也可能破坏系统的稳定性。

微分环节。由于此处以变化率作为依据，因此能起到一定的预测作用，在变化发生前就能给出一个提前的校正信号。但由于其对变化率敏感，可能导致系统震荡。

通过对这3个环节工作特点的分析，并结合凸轮磨削的实际经验，经过反复的调整和实验，可编译出较为理想的模糊推理规则，该规则反映了仿形跟踪误差及仿形跟踪误差变化率在各种可能的工作情况之下，PID 3个参数各自变化的趋势。建立Δkp、Δki、Δkd的模糊规则(见表1～表3)。

表1 Δkp模糊规则表Tab.1 Sheet ofΔkp's fuzzy rules

表2 Δki模糊规则表Tab.2 Sheet ofΔki's fuzzy rules

表3 Δkd模糊规则表Tab.3 Sheet ofΔkd's fuzzy rules

Δkp、ΔkiΔkd的非线性对应关系如图11所示。

图11 Δkp、Δki、Δkd与E及Ec的非线性对应关系Fig.11 Nonlinear corresponding relations betweenΔkp，Δki，Δkdand E，Ec

3 仿真实验

笔者运用Matlab中Simulink以及fuzzy工具箱搭建磨削系统［13-16］。由于凸轮的误差与两轴的运行速度有关，通常磨削速度越快，仿形跟踪误差越大，相应的轮廓误差也越大。为了验证补偿器的补偿效果，可将实验条件设为恒转速磨削，C轴转速可设为10°/s。为验证控制器的鲁棒性，于C轴转角为200°的时刻，分别在主导轴C轴和进给轴X轴加入阶跃扰动，观察其抗扰性能。

图12和图13是扰动发生在C轴时，仅反馈无控制器、常规PID及模糊PID几种情况下仿形跟踪误差的对比图。可以看出，仅利用笔者提出的仿形跟踪误差补偿方式，仿形跟踪误差e能控制在10μm以内，结合常规PID控制器，该补偿方式又将仿形跟踪误差降低到5μm以内。图13可以观察到各种方案抗扰性能的差异，与其他两种方案相比，结合模糊PID的跟踪补偿让系统的鲁棒性更加理想。

为了进一步验证控制器的性能，改变实验条件，扰动发生在进给轴X轴时，观察仿形跟踪误差的变化。图14、图15为扰动发生在x轴时系统抗扰性能对比图。同样是在主导轴C轴转角为200°的时刻加入扰动，从图14和图15可以看到，没有扰动时，仅采用仿形跟踪误差补偿方式而不结合任何控制器，仿形跟踪误差是10μm以内，而结合控制器的后两种方案均能将仿形跟踪误差限制在5μm以内;在200°时刻X轴发生扰动后，结合模糊PID控制器的仿形跟踪误差补偿方式仍能将仿形跟踪误差控制在5μm以内，而其他两种方案均无法达到这个精度。

图12 C轴有扰动时仿形跟踪误差对比图Fig.12 The diagram of profiling tracking error comparison when C axiswith disturbance

图13 C轴有扰动时系统抗扰性能对比图Fig.13 The diagram of anti-disturbance performance comparison when C axiswith disturbance

图14 X轴有扰动时仿形跟踪误差对比图Fig.14 The diagram of profiling tracking error comparison when X axiswith disturbance

图15 X轴有扰动时系统抗扰性能对比图Fig.15 The diagram of anti-disturbance performance comparison when X axiswith disturbance

4 结 语

通过对凸轮轮廓误差与仿形跟踪误差关系的研究，提出了计算简单、易于实现的新补偿方式-仿形跟踪误差补偿，建立了在线反馈仿真系统，利用仿形跟踪误差补偿结合模糊PID控制器设计了凸轮磨削轮廓误差补偿器。通过仿真实验验证，该方案不仅能有效提高跟踪轴X轴对主导轴C轴的跟踪性能，而且对外界的干扰，模糊PID较常规PID具有更好的鲁棒性，从而能有效降低系统的仿形跟踪误差，进而减小凸轮的轮廓误差，提高了凸轮的磨削精度。另外，砂轮的转速和切削量是影响凸轮表面光滑程度的关键，高速、超高速磨削是数控加工领域的一个研究方向，将砂轮转速、切削量及温度等影响工件表面质量的参数共同考虑是今后需着重研究的问题。

［1］赵希梅，郭庆鼎.为提高轮廓加工精度采用DOB和ZPETC的直线伺服鲁棒跟踪控制［J］.电工技术学报，2006，21(6):111-114. ZHAO Ximei，GUO Qingding.Linear Servo Robust Tracking Control Based on DOB and ZPETC to Improve the Contour Machining Precision［J］.Transactions of China Electrotechnical Society，2006，21(6):111-114.

［2］KOREN Y.Cross-Coupled Biaxial ComputerControl for Manufacturing Systems［J］.Journal of Dynamic Systems，Measurement，and Control，1980，102(4):265-272.

［3］TIAN X Q，HAN J，XIA L.Precision Control and Compensation of Helical Gear Hobbing via Electronic Gearbox Cross-Coupling Controller［J］.International Journal of Precision Engineering＆Manufacturing，2015，16(4):797-805.

［4］陈永亮，韩瑶，刘谱，等.五辊式无溶剂涂布系统交叉耦合建模与设计方法 ［J］.工程设计学报，2014，21(1):38-42，50.CHEN Y L，HAN Y，LIU P，et al.Mechatronic Cross-Coupling Modeling and Design Method for Five-Rollers Solventless Coating System［J］.Chinese Journal of Engineering Design，2014，21(1):38-42，50.

［5］SUN J，TIAN L，LIU W，et al.Cross-Coupling Adaptive Control for the System of DC Servo XY Table［J］.Journal of Shenyang Jianzhu University，2013，29(4):733-738.

［6］李圣怡，张云洲，张明亮，等.超精密机床的变增益交叉耦合控制研究［J］.基础自动化，2000，7(2):25-28. LIShengyi，ZHANG Yunzhou，ZHANG Mingliang，et al.The Research on Variant Gain Cross Coupling Control of Ultra-Precision CNCMachine［J］.Basic Automation，2000，7(2):25-28.

［7］SU K H，CHENGM Y.Contouring Accuracy Improvement Using Cross-Coupled Control and Position Error Compensator［J］. International Journal of Machine Tools and Manufacture，2008，48(12):1444-1453.

［8］龚时华，黄禹.凸轮轴磨削加工轮廓误差的自适应控制［J］.电气自动化，2010，32(4):1-3. GONG Shihua，HUANG Yu.Adaptive Control of Cam Contour Error in Camshaft Grinding Process［J］.Electric Drive＆Automatic Control，2010，32(4):1-3.

［9］王立新，王迎军.模糊系统与模糊控制教程［M］.北京:清华大学出版社，2003. WANG Lixin，WANG Yingjun.A Course in Fuzzy Systems and Control［M］.Beijing:Tsinghua University Press，2003.

［10］张化光，何希勤.模糊自适应控制理论及其应用［M］.北京:北京航空航天大学出版社，2002. ZHANG Huaguang，HE Xiqin.Theory and Application of Fuzzy Adaptive Control［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2002.

［11］苏明，陈伦军，林浩.模糊PID控制及其MATLAB仿真［J］.现代机械，2004(4):51-55. SU Ming，CHEN Lunjun，LIN Hao.Study of Fuzzy PID Control［J］.Modern Machinery，2004(4):51-55.

［12］孙怡.基于模糊PID控制的多电机同步控制系统的研究［D］.上海:华东理工大学机械与动力工程学院，2012. SUN Yi.Multi-Motor's Synchronization Control System Based on Fuzzy-PID Control［D］.Shanghai:School ofMechanical and Power Engineering，East China University of Science and Technology，2012.

［13］SUI Z，GUO M，LIU H，et al.Modeling and Simulation Analysis of NC Camshaft Grinding System［C］∥Digital Manufacturing and Automation(ICDMA)，2011 Second International Conference on.Los Alamitos:IEEE，2011:732-738.

［14］王勋龙，张红燕，隋振，等.数控凸轮磨削中三环控制系统设计［J］.吉林大学学报:信息科学版，2012，30(1):40-46. WANG Xunlong，ZHANG Hongyan，SUIZhen，etal.Design of Three Loop Control System in NCCam Grinding Process［J］. Journal of Jilin University:Information Science Edition，2012，30(1):40-46.

［15］郭盟.凸轮磨削的建模与控制［D］.长春:吉林大学通信工程学院，2012. GUO Meng.Modeling and Control of Cam Grinding［D］.Changchun:College of Communication Engineering，Jilin University，2012.

［16］隋振，郭盟，王勋龙，等.凸轮轴磨床OEM软件的二次开发及算法设计［J］.吉林大学学报:信息科学版，2010，28(5):519-525. SUIZhen，GUO Meng，WANG Xunlong，et al.The Re-Development of OEM Software and Algorithm Design in Camshaft Grinder［J］.Journal of Jilin University:Information Science Edition，2010，28(5):519-525.

(责任编辑:刘俏亮)

Profile Tracking Error Compensation for Cam Grinding

SUIZhen，LICong，WANG Jing
(College of Communication Engineering，Jilin University，Changchun 130022，China)

To improve the precision of cam grinding machining，reduce the cam contour error，and improve the robustness of the system，a new error compensation method is adopted.It is named profiling tracking error compensation，in which the actual profiling tracking error compensate the series values of X axis.The two axes linkage feedback system is established by using Matlab，and the fuzzy PID(Proportional-Integral-Derivative) controller is designed to realize online compensation for the system.The cam used in the simulation experiment is difficult to process so as to verify compensation effects and the performance of the controller.The simulation experimental results show that thismethod can effectively reduce the cam contour error，simplify the calculation process，and improve the response speed of the system.Compared with the traditional PID controller，it has better robustness.

profiling tracking error compensation; cam grinding; fuzzy-proportional-integral-derivative (PID);robustness

TP273.4

A

1671-5896(2015)06-0644-08

2015-05-22

吉林省科技厅基金资助项目(20150101031JC);吉林大学基本科研业务费基金资助项目(201003056)

隋振(1970— )，男，吉林公主岭人，吉林大学副教授，博士，硕士生导师，主要从事复杂系统建模、优化与控制研究，(Tel)86-13604312078(E-mail)suizhen@jlu.edu.cn;通讯作者:王静(1990— )，女，河北邯郸人，吉林大学博士研究生，主要从事凸轮磨削的研究，(Tel)86-13943135320(E-mail)jingw14@mails.jlu.edu.cn。