A simple approach for bubble modelling from multiphase fluid simulation

Bo Ren(),Yuntao Jiang,Chenfeng Li,and Ming C.Lin

©The Author(s)2015.This article is published with open access at Springerlink.com

A simple approach for bubble modelling from multiphase fluid simulation

Bo Ren1(),Yuntao Jiang2,Chenfeng Li3,and Ming C.Lin4

©The Author(s)2015.This article is published with open access at Springerlink.com

This article presents a noveland flexible bubble modelling technique for multi-fluid simulations using a volume fraction representation.By combining the volume fraction data obtained from a primary multi-fluid simulation with simple and efficient secondary bubble simulation,a range of real-world bubble phenomena are captured with a high degree of physical realism,including large bubble deformation, sub-cell bubble motion,bubble stacking over the liquid surface,bubble volume change,dissolving of bubbles, etc.Without any change in the primary multi-fluid simulator,our bubble modelling approach is applicable to any multi-fluid simulator based on the volume fraction representation.

bubble; volume fraction; smoothed particle hydrodynamics;fluid simulation

1 Introduction

Real-world liquids often contain bubbles,interacting and evolving together in various forms.For example, vibrant bubbles are generated when gas is quickly trapped or injected into a liquid,while flickering tiny bubbles occur when a liquid slowly releases dissolved gas.Bubbles can also behave very differently inliquids.Big bubbles can change shape due to liquidgas interaction.In certain solutions such as soapsuds,stacked bubbles can be observed covering the liquid surface.When gas can dissolve in a liquid,bubble size can change dynamically and small bubbles can dissolve and disappear due to liquid motion.Bubbles also quickly,if not immediately,pop when they rise and reach the liquid surface,and in the case of bubble stacking,the pushed-up bubbles pop first due to surface liquid loss.These varying dynamic phenomena contribute to the rich visual effects caused by liquid-gas interaction.

Various approaches have been proposed to model bubbles,especially bubble generation and tracking.A Eulerian surface tracking framework can be used for large bubble motion and deformation[1], and this can be further improved by introducing supplementary particles[2].Particles are also used to directly represent small(sub-cell)bubbles,to simulate bubble motion,and to add spray effects[3, 4].While the uprising motion of bubbles is often simulated by directly adding buoyancy and drag forces,more complex methods that capture the liquid-gas interaction more accurately can introduce physical realism,such as using two-way coupling models[5,6].

From the viewpoint of physics,bubbles can be considered asa specialtypeofinterfacial multi-phase flow phenomena involving immiscible liquid and gas.In this sense,recent progress in multi-fluid simulation using the volume fraction representation[7,8]has the potential to benefit bubble modelling.While fully capturing the liquid-gas interaction,the volume fraction data accurately describe gas distribution through the whole simulation space,which in turn determines bubble distribution and volume change.Specifically,in the presence of bubbles,the local volume can be dominated by the gas phase,but due to the high density ratio between liquid and gas phases,the local average mass of gas is typically small compared to the liquid mass.Thus,bubbles can be automatically detected through the disagreement between mass and volume fractions,which fits nicely into the volume fraction representation framework.However, there has been little research taking advantage of such advanced volume fraction-based multi-fluid simulation for modelling bubble effects.

Our novel method can model various bubble effects in multi-fluid simulations using the volume fraction representation.Based on the volume fraction data,regions where the mass fraction is dominated by gas are categorized as gas regions or large bubbles,and they can be tracked with isosurfacebased reconstruction methods.Sub-grid bubbles are modeled using a low-cost secondary simulation, where the volume and movements of bubbles are determined from the results of the primary multifluid simulation.This new approach has the following advantages:(1)it is simple and efficient,needing no change to the primary simulator,and has the flexibility to integrate bubble effects into existing multi-fluid simulation results without the need for re-simulation;(2)it can simultaneously handle various bubble effects including deformation of large bubbles,volume change,dissolution,stacking of sub-cell bubbles,etc.;(3)the result can naturally captureliquid-gasinteraction taking advantage of advanced multi-fluid simulation,with bubble distribution consistent with the physical gas fraction distribution.We demonstrate the effectiveness of the proposed approach with both SPH and grid-based multi-fluid simulations.

The rest of the paper is organized as follows.In Section 2,we review related work.In Section 3,we introduce our bubble generation algorithm based on the volume fraction representation.We describe implementation detail in Section 4 and results in Section 5.We conclude by discussing the benefits and limitations of the new approach in Section 6.

2 Previous work

Traditionally,graphics research has focused on direct bubble simulation.A Eulerian grid is used to simulate large bubbles in liquids,where the shapes and deformation of bubbles can be tracked using the level-set method.This allows various visual effects to be produced for large bubbles[1,9,10].Certain stacking effects for large bubbles over a liquid surface can also be modeled,e.g.,see Refs.[11,12].To facilitate bubble generation and shape tracking, Lagrangian particles were later introduced into some hybrid simulation methods[2,13-16],where sub-cell bubbles and foam are taken into account.

Alternatively,Lagrangian particles are extensively used to represent small sub-cell bubbles in particlebased bubble simulation methods using the smoothed particle hydrodynamics(SPH)framework,where larger bubbles are usually reconstructed using a collection of neighboring gas particles[17,18].By adding cohesive forces between bubble particles and the liquid,dynamic bubble movements and stacking foamscan besimulated,producingimpressive results[3,19,20].In these works,the motions of sub-cell bubbles are mostly modelled with oneway influenced[3,19]or two-way coupled [14, 20]particles based on various types of drag and cohesive forces;the sub-cell bubbles have limited influence on the liquid motion.For simulation ofdispersed bubbles beneath a liquid surface, Ref.[5]proposed a variable-density Poisson solver, wherethe localaveragedensity and pressure are influenced by bubble concentration.They also provided a stochastic solver to approximate microscale motions.Later,Ref.[6]derived a monolithic approach,where bubble volumes can change,and liquid and gas motions tightly affect each other.However,bubble stacking is not modeled by their approach.Instead of directly simulating all bubble motions,Ref.[4]used a secondary simulation that generates spray,foam and small bubble effects from the primary single-phase Lagrangian simulation result.Our approach is somewhat similar to theirs in thatwe also do notdirectly simulate all bubble motions.Based on a primary multi-fluid simulation,we reconstruct bubbles of different sizes from the fraction field,and control volume change, dissolution,and motion of bubbles in a secondary simulation which does not influence the primary simulator.In comparison to direct bubble simulation, our approach can reproduce various bubble effects in a simple and efficient way.It not only reproducesbubble phenomena in which the bubble properties, distribution,and movement faithfully reflect the physical gas distribution and liquid-gas two-way coupling,but it also physically captures the liquid motion influenced by the gas phase thanks to the primary multi-fluid simulation.Our approach is very flexible in that it can be applied to existing multifluid simulation data to integrate additional bubble effects without the need for re-simulation.

Graphics fluid simulators using a volume fraction representation date back to Ref.[17].Later,the volume fraction representation was combined with adiffusion modeltosimulatemulti-fluid behaviors,both for grid-based solvers[21,22]and for SPH-based solvers[23].More recently,multifluid simulators that consider the velocity difference between phases have been proposed to bring in morephysicalrealism [7,8].In computational fluid dynamics(CFD),all commercial multi-fluid simulators(such as ANSYS CFX and FLUENT)are based on the volume fraction representation.Our approach does not rely on a specific multi-fluid simulator,as long as it uses the volume fraction representation and can handle physical simulation of liquid-gas mixtures.

3 Bubble modelling from volume fraction data

The volume fraction representation in multi-fluid simulation describes the spatial distribution of the simulated phases via their fraction fields.At any point in the simulation domain,the fraction of volume locally occupied by a phase k is its volume fraction αk;similarly,the local fraction of mass of the phase k is its mass fraction ck.Given the rest density of each phase,these two fraction values can be calculated from each other.Multi-fluid simulators using a volume fraction representation usually do not directly track the interface between different phases,but the spatial fraction field can still provide direct indication of the distribution of each individual phase.On the other hand,it is often difficult to clearly define and track sub-cell bubbles whose interface geometry is finer than the simulation resolution.The motions of these bubbles also physically couple with the fluid motion on a sub-cell level.This indicates that volume fractionbased multi-fluid simulators may be useful for visual simulation of bubbles.

3.1 Categorizing bubbles

In the physical world,the density ratio of liquid to gas is often high(varying from 100:1 to 1000:1).In the volume fraction representation,this leads to an obvious difference in the values of the gas volume fraction and the gas mass fraction.Thus,when there is locally little gas present,the volume fraction and the mass fraction of gas are both small;however, as the local gas phase increases,its volume fraction rises,while its mass fraction remains low due to the high density ratio between liquid and gas;this can be the case even when the gas volume fraction is more than 0.95.Finally,when the liquid phase is mostly expelled locally,the mass fraction of the gas then rises.

On the other hand,real-world bubbles,especially stacked bubbles over a liquid surface,have particular properties:the volume is largely contributed by entrapped gas,but the mass is largely contributed by the liquid forming the bubble surface.Based on these observations,we propose a simple rule to categorize bubbles into three groups:small,medium,and large bubbles.Specifically,if the gas volume fraction αgis lower than a given threshold θ1,we consider the local space to be mainly occupied by the liquid phase, and only dispersed and relatively small bubbles exist, which we classify as small bubbles.If the gas volume fraction αgis higher than θ1,but the gas mass fraction cgis lower than a given threshold θ2,middlesized bubbles are present in the liquid,or bubbles are stacked over the liquid surface.We classify this case as medium bubbles.Finally,if the gas mass fraction cgis higher than θ2,the location is either outside the liquid,or belongs to a large bubble region in the liquid.

Fig.1 Overview of bubble modelling strategy in a multi-fluid simulation using a volume fraction representation.Different types of bubbles are categorized according to the volume fraction field data in the primary simulation.Bubbles are either directly generated or created through a secondary simulator depending on their categories;the primary simulation is not affected.

An overview of our approach is presented in Fig.1.Large bubbles can be conveniently generated from the simulation data through isosurface-based surface reconstruction methods.Since the multifluid simulator takes care of physical changes in the fraction field,we can directly determine deformation and volume changes(merging and splitting)for large bubbles.Medium and small bubbles often have sub-cell sizes,so it is better to directly represent them.For simplicity,we follow traditional approaches using sphere-shaped sub-cell bubbles for rendering.However,bubble shapes can be further improved by a recent rendering technique[6]which uses a dictionary of level sets.Bubbles can come into contact as they get closer.It is possible to simply merge them into a larger bubble,but in the cases of multiple contacts,which often happen for stacking bubbles,this is not the best choice.Moreover,not all bubbles in contact have an original distribution like a sphere,and the newly merged larger bubble may in turn collide with other bubbles,resulting in distribution errors.Thus,instead of merging colliding bubbles,we adopt the tessellation method from Ref.[19],wherebubblesin contactare represented using a weighted Voronoi diagram.This tessellation method is only used to regenerate the contact-surface mesh,and does not affect general bubble motion and position determination,or the volume change handling process,even in the case of bubble-stacking phenomena.

3.2 Controlling bubble volume

Bubbles may experience volume change in the liquid forseveralreasons.Since gasismore compressible than liquid,bubbles usually expand when rising.Bubble sizes also change in the cases of merging or splitting.All gases are soluble in liquid to a certain extent.As a result,bubbles can change volume when moving through liquid, absorbing undissolved gas or losing some of its own due to solution;small bubbles may totally dissolve in the liquid and disappear.

Fortunately the volume fraction representation provides a straightforward way to evaluate bubble volume changes.Specifically,the bubble volume must satisfy the following relation:

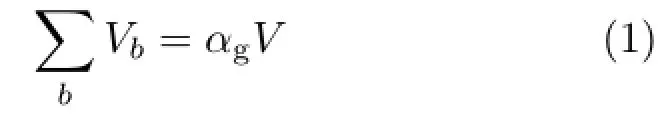
where Vbis the volume of bubbles,αgis the local gas volume fraction,and V is the local volume.The sum is taken over all bubbles b in the local volume V.

The above equation indicates that three main factors affect bubble volume.The first is the local gas volume fraction at the bubble location,which affects all three types of bubbles.Intuitively,if the gas volume fraction is high,there is more gas in the local region,and the bubble volume can be larger.The second factor is the local volume V,which may change in Lagrangian simulators when the effective particle volume varies over time.The last factor is the local number of bubbles.Each bubble has a smaller share of the volume if there are more bubbles in the local space.This mostly affects small bubbles, since these bubbles are most likely to be dispersed in the liquid and to share the same local volume.

4 Implementation

In this section we now describe in detail howwegeneratemulti-sized bubblesbased on the principles introduced in Section 3,as well as how to derive volume changes and motions of the bubbles from the primary simulation data.In Lagrangian simulators,particles in the primary simulation provide a reference of bubble position,but in Eulerian multi-fluid simulatorsusingavolume fraction representation,there are no Lagrangian particles.Thus although the general framework does not differ greatly,the specific calculations needed using these two types of simulators are slightly different,as we explain in the following.

4.1 Lagrangian simulator

Among different Lagrangian methods,the SPH framework is the most widely used one in computer graphicsforbubblesimulation and multi-fluid simulation,so we mainly refer to SPH formulation in this section.

Firstly,we consider small bubbles,appearing in locations where the gas volume fraction is low and the local volume is mostly occupied by the liquid phase.From Eq.(1),we need to determine all three factors for small bubbles in a Lagrangian primary simulation.Following the standard SPH formulation, the interpolated volume fraction of gas for a particle i is

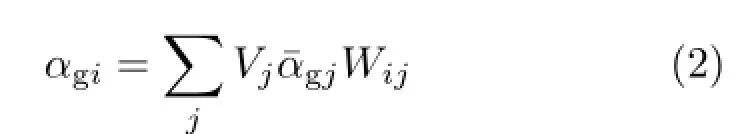
The definition of volume fraction gives

where Vgjis the gas volume of particle j.Thus, Eq.(2)can be rewritten as

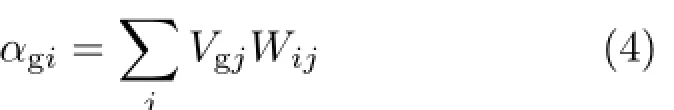
We now treat the small bubbles in a secondary simulation.For a fluid particle i in the primary simulation,we can apply the following equation to small bubble particles b: where Vbis the volume of small bubble b in the secondary simulation.Summation is performed over all small bubble particles b in the neighborhood of particle i.Only those fluid particles in the primary simulation with gas volume fraction lower than θ1require this interpolation.

Equation (5) provides an estimate of the interpolated volume fraction at the position of particleidueto existing smallbubbles.The difference between this estimate and the true value of αgof particle i can be used for generating new small bubbles and volume adjustment of existing small bubbles.Intuitively,if the estimated value is larger than the true value in the primary simulation, volumes of nearby small bubbles may be too large,or the small bubbles may be over-populated,and vice versa.

We still need to determine the local volume and number of bubbles in the local volume,used in Eq.(1).For each small bubble in the secondary simulation,we find the nearest fluid particle in the primary simulation in space.At the same time,for each fluid particle in the primary simulation with volume fraction of the gas phase lower than θ1,we count the number n of small bubbles for which it is the nearest particle.In this way,each fluid particle in the primary simulation with gas volume fraction lower than θ1defines a local volume using its own volume Vi=mi/ρi0,where miis the mass of particle i,and ρi0is its current rest density;the number of bubbles in this local volume is just n.

The volume change for a small bubble particle b in the secondary simulation is given by

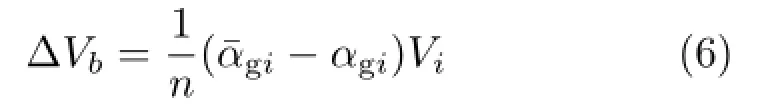
Whenever Vb＜ 0,the small bubble particle in the secondary simulation is removed.A small bubble particle will also be directly removed if the nearest particle it finds does not satisfy the condition that the gas volume fraction is lower than θ1,which indicates it has travelled too far into another region.

After adjusting existing small bubble particles, we recalculate Eq.(5)for each fluid particle in the primary simulation with gas volume fraction lower than θ1.If

where∈∈[0,1)is a control factor,then a new small bubble particle is added to the secondary simulatorat the position of particle i.The volume of the new small bubble is

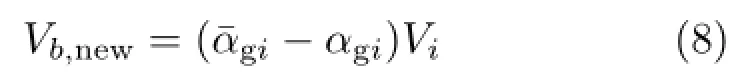
The smallbubble particles in the secondary simulation are advanced by the velocity of its nearest primary particles,or they can be advanced with the gas velocity if the phase velocity is provided by the primary simulator.When the relative positions of the secondary bubble particle and its nearest primary fluid particle change,which results in falling value of the smoothing kernel,the non-zero control factor∈serves to prevent frequent particle adding due to such effect.We set∈=0.5,but it can be freely adjusted depending on needs.

Medium bubbles does not need to be handled in the secondary simulator.For Lagrangian primary simulators it is convenient to attach a medium bubble to those primary fluid particles that have gas volume fraction larger than θ1but gas mass fraction smaller than θ2.The volume of the medium bubbles is set to Vb= ¯αgiVi.This has the advantage that for large gas volume fraction values,fluctuations in SPH interpolation typically result in frequent adding and deleting of secondary particles,while directly attaching each medium bubble to the corresponding primary fluid particle avoids this issue.The fact that secondary simulation is not needed also provides computational efficiency as there is no need for interpolation calculations.Note that the size of a medium bubble changes with the volume fraction of the primary fluid particle,and a medium bubble will move with the primary fluid particle it is attached to.

Finally,primary fluid particles with gas mass fraction larger than θ2automatically form large bubbles via isosurface-based surface reconstruction methods,e.g.,the anisotropic kernel method[24].

4.2 Eulerian simulator

As is done in secondary simulation for Lagrangian simulators, we can add Lagrangian particles representing small and medium bubbles into a secondary Eulerian grid,and calculate the volume and motion of bubbles using primary simulation data.Here,the secondary simulation also starts by updating the volume of existing bubbles.The local volume in Eq.(1)can be conveniently chosen as the grid cell volume V,and the number of secondary particles n located in each cell serves as the number of bubbles in the local volume.A proper update method should include volume expansion and shrinking,and bubble addition and deletion effects during the computation.

Suppose a secondary particle with volume Vb,tmoves from a cell with gas volume fraction αg,t−1to a cell with gas volume fraction αg,t.We first update its volume using

Then,within each cell,we calculate

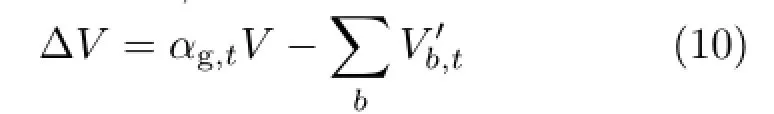
where summation is taken over all bubble particles in the grid.If ΔV≤0,an amount ΔV/n is subtracted from all bubble particles inside the cell;if ΔV ＞0,a new secondary bubble particle with volume ΔV is added at a random position within the cell.Whenever a secondary particle has volume less than zero or it enters a cell with gas mass fraction larger than θ2,the particle is removed from the secondary simulation.After updating particle volumes,they are advanced by the fluid or gas velocity at their locations.This strategy is illustrated in Fig.2.

The above strategy is used for both small and medium bubbles in grid-based simulators.For large bubbles and liquid surface reconstruction,isosurface methods similar to those in Ref.[9]can be used,with the user-defined threshold value determined by the gas volume fraction.

4.3 Bubble reconstruction framework

For Lagrangian and Eulerian multi-fluid simulation methods,the generation of bubbles from the primarysimulation shares the same framework.Regions with high gas mass fraction are treated as large bubbles and reconstructed using isosurface methods.Small bubbles are handled in a secondary simulation, whose framework is shown in Algorithm 1,and whose methods were described in detail in Sections 4.1 and 4.2.There are slight differences in the specific calculations between Lagrangian and Eulerian simulations,mostly due to the fact that Lagrangian simulations have built-in particle systems that can be conveniently used to indicate bubbles but Eulerian simulations do not.The local volume is defined by the cell volume in the Eulerian simulation,while it is defined by the primary fluid particles’own volumes in the Lagrangian simulation.Although we could define“medium bubble regions”for Eulerian simulation using θ1and θ2,it is more convenient to handle medium bubbles via secondary simulation.

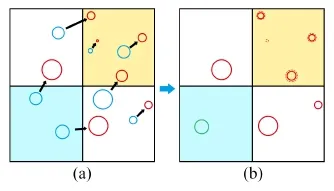
Fig.2 (a)Volumes of existing bubbles are adjusted when they are advanced.Some cells may be over-populated(lightyellow)or contain insufficient bubble volume(light-blue).Blue circles indicate previous positions and volumes of bubbles;red circles indicate their current positions and volumes.(b)In overpopulated places,bubble volumes are corrected downwards, and in underpopulated places,a new bubble is generated(green circle).

Algorithm 1:Secondary simulation

The values of θ1and θ2are user-defined and relate to the density ratio between liquid and gas.We find that setting θ1∈[0.1,0.5],θ2∈[0.05,0.5]usually gives satisfactory results in our experiments when the liquid-gas density ratio is above 100:1.

The particle deletion step in Algorithm 1 can delete bubbles in two situations.When a bubble rises above the liquid surface,it can be deleted either due to rapid drop of liquid fraction or by entering into the gas phase region.This captures bubble popping that occurs at the liquid surface in the real world.Large amounts of bubbles rising can result in appearance of frequent popping when they reach the liquid surface,which should not be viewed as a flickering artifact caused by immediate deletion of newly generated bubbles.The second situation is that small bubbles can naturally be deleted due to negative volume change.From a physical point of view,this corresponds to cases where gas gets dissolved in the liquid or smaller bubbles get absorbed by larger ones.On the other hand,for rendering efficiency,it is not economical to keep bubbles smaller than one pixel.Deleting smaller bubbles beforehand is more practical than keeping every existing bubble.

5 Results

The secondary simulation only involves local computations,so can be readily parallelized on the GPU given the primary simulation data.We have implemented the secondary simulator using CUDA 6.5 on an NVIDIA GeForce GTX 980 graphics card.The computational time tends to be more costly for Lagrangian simulators due to its neighborhood interpolations.However it generally adds only a small overhead to the primary multifluid simulation.In our examples the secondary simulation adds less than 4%computational time to the primary simulation.The figures in this section can be enlarged in the online version to see further details,while a supplementary video is also provided online to demonstrate the examples in the Electronic Supplementary Material.

Figure 3 shows gas rising in a soap solution simulated using a Lagrangian simulator.Vigorously evolving bubbles of multiple sizes are formed as gas rises up,with tight liquid-gas coupling in the solution.There are about 3000 small bubbles and 6000 medium bubbles(not counting those that have broken or dissolved).Each rendered frame incorporates 8 simulation steps;secondary simulation takes 56 ms per frame(at a rate of 25 frames per second).Realistic deformations of large bubbles,sub-cell bubble motion within the liquid,and stacking bubbles on the liquid surface are generated using the proposed approach.The bubbles automatically burst and disappear at the top when the liquid fraction drops below the threshold.

Figure 4 shows the same case but omits the small bubbles in the secondary simulation.While there are many fewer sub-cell small bubbles,but the stacking effects and deformation and motion of large bubblesare preserved.Omitting the secondary simulator, the bubble processing is simplified while preserving many interesting visual effects.

Fig.3 Bubbles in a soap solution.Gas is injected from bottom center,creating bubbles of various sizes.Realistic bubble volume evolution,stacking,and bursting are recovered by our approach.

Fig.4 Bubbles in a soap solution.Only the medium and large bubbles are rendered.While fewer sub-cell bubbles exist in the result,the stacking effects and deformation and motions of large bubbles are preserved.

Figure 5 simulates a scene with two transparent chemical solutions meeting and reacting to produce gas(e.g.,hydrochloric acid and sodium carbonate solution reacting to produce carbon dioxide)using a Lagrangian simulator.It contains about 7000 medium bubbles.Realistic bubble effects are produced using the proposed approach.Bubbles are quickly generated in the reacting region,and form a thin layer over the liquid surface during continuous generation and bursting.

Figure 6 shows a bubbly liquid-gas mixture running through a pipe containing a small boxshaped obstacle.The primary simulation used an ANSYSCFX Euleriansimulator,and139,000 bubbles were recovered from an effective 20× 20×100 grid.Each rendered frame incorporated 5 simulation steps;secondary simulation took 33 ms per frame.The volume ratio of water to gas was set to 7:3 at the left inlet of the pipe.In such a mixture containing dense bubbles,the gas motion is heavily coupled to the liquid motion while the gas velocity differs greatly from the water velocity.The fully-rendered result at the top row shows that the bubble distribution is consistent with the physical distribution of gas in the simulation;the partlyrendered result at the bottom row shows more clearly how the varying sizes and motions of different bubbles are reproduced.The water surface mesh is unchanged in the latter case:only certain bubbles are omitted during the rendering process.

6 Conclusions

Fig.5 Reacting bubbles.Two transparent solutions meet and react at the center,producing gas.Bubbles are quickly generated in the reaction region,and form a thin layer over the liquid surface during continuous generation and bursting.

Fig.6 Bubbly liquid-gas mixture running through a pipe containing a small box-shaped obstacle.Top: all bubbles are rendered.Distribution of the dense bubbles is consistent with the gas volume fraction distribution in the primary simulation.Bottom: only one out of every 30 bubbles is rendered.Each bubble moves differently according to the physical velocity and has varying volume during its motion.

We have presented a novel and efficient bubble modelling strategy for multi-fluid simulation using volumefraction representation.Through simple and efficient computations,various bubble effects can be recovered from the primary simulation data without any changes required to the primary simulator.These include deformation oflarge bubbles,volume changes,dissolving of bubbles, and stacking of sub-cell bubbles.In the results, the bubble motions and liquid motions naturally reflect the two-way coupled liquid-gas interaction, while the bubble distribution is also consistent with the physical gas distribution in the primary simulation.The proposed bubble modelling approach can be easily and independently applied to any multi-fluid simulator based on a volume fraction representation,and is able to integrate bubble effects into existing multi-fluid simulation data without the need for re-simulation.The idea of utilizing fraction fields for region recognition could also be useful in recovering other natural phenomena such as mud sliding,efflorescence,dissolution,and crystallization, offering several future research directions.

The current strategy only produces at most one single bubble within each local volume if possible.However,in somecases,itmaybe desirableto generatemultipletiny bubblesat thesametime,using certain patterns.Fora Lagrangian simulator,when a primary fluid particle is considered to be attached by a medium bubble, multiple smaller bubbles may actually exist in the local volume,which is not considered by our approach.Further investigation of these aspects could potentially enhance the flexibility of the proposed approach.Also for Lagrangian simulators, although the bubble distribution largely correspondsto the physical gas distribution,they are not exactly the same.In principle,iterating the volume correction and particle addition steps could reduce errors,and feedback to the primary simulator could also be adopted.However,the marginal improvements may not be worth the more complex computations involved.

Since bubble positions and volumes are calculated from the primary simulation data,the total bubble volume may change slightly after Voronoi tessellation,losing some overlapped volumes.This mostly affects medium bubbles in Eulerian simulations where no pressure force propels particles when they become too close to each other.Although such volume loss can to some extent reflect the weakly compressible feature of gas in the Lagrangian simulation,neighborhood contact detection and volume correction strategies may be desired to alleviate this problem for the Eulerian simulation,but at a higher computational cost.

Currently bubble motion is purely driven by the primary simulation,and providing feedback into the primary simulation may facilitate bubble buoyancy.Phenomenawithverylargebubbles stacked above the liquid surface(as in previous work [11])arenotcaptured by ourproposed approach,since these regions with very large bubbles will tend to be detected as gas regions.

Acknowledgements

This work was supported by the National High Technology Research and Development Program of China(No.2013AA013903),the National Natural Science Foundation of China(No.61120106007), Research Grant ofBeijing Higher Institution Engineering Research Center, and Tsinghua University Initiative Scientific Research Program. It was also supported in part by the U.S.National Science Foundation and the University of North Carolina Arts&Sciences Foundation.

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited. Electronic Supplementary MaterialSupplementary material is available in the online version of this article at http://dx.doi.org/10.1007/s41095-015-0020-6.

[1]Hong,J.-M.;Kim,C.-H.Discontinuous fluids.ACM Transactions on Graphics Vol.24,No.3,915-920, 2005.

[2]Kim,P.-R.;Lee,H.-Y.;Kim,J.-H.;Kim,C.-H. Controlling shapes of air bubbles in a multi-phase fluid simulation.The Visual Computer Vol.28,No.6,597-602,2012.

[3]Cleary,P.W.;Pyo,S.H.;Prakash,M.;Koo,B.K. Bubbling and frothing liquids.ACM Transactions on Graphics Vol.26,No.3,Article No.97,2007.

[4]Ihmsen,M.;Akinci,N.;Akinci,G.;Teschner,M. Unified spray,foam and air bubbles for particle-based fluids.The Visual Computer Vol.28,No.6,669-677, 2012.

[5]Kim,D.;Song,O.-y.;Ko,H.-S.A practical simulation ofdispersed bubbleflow.ACM Transactionson Graphics Vol.29,No.4,Article No.70,2010.

[6]Patkar,S.;Aanjaneya,M.;Karpman,D.;Fedkiw,R. A hybrid Lagrangian-Eulerian formulation for bubble generation and dynamics.In: Proceedings of the 12th ACM SIGGRAPH/Eurographics Symposium on Computer Animation,105-114,2013.

[7]Nielsen,M.B.;Osterby,O.A two-continua approach to Eulerian simulation of water spray.ACM Transactions on Graphics Vol.32,No.4,Article No.67,2013.

[8]Ren,B.;Li,C.;Yan,X.;Lin,M.C.;Bonet,J.;Hu, S.-M.Multiple-fluid SPH simulation using a mixture model.ACM Transactions on Graphics Vol.33,No.5, Article No.171,2014.

[9]Hong,J.-M;Kim,C.-H.Animation of bubbles in liquid. Computer Graphics Forum Vol.22,No.3,253-262, 2003.

[10]Mihalef,V.;Unlusu,B.;Metaxas,D.;Sussman, M.; Hussaini, M. Y. Physics based boiling simulation.In: Proceedingsofthe 2006 ACM SIGGRAPH/Eurographics symposium on Computer animation,317-324,2006.

[11]Kim,B.;Liu,Y.;Llamas,I.;Jiao,X.;Rossignac,J. Simulation of bubbles in foam with the volume control method.ACM Transactions on Graphics Vol.26,No. 3,Article No.98,2007.

[12]Zheng,W.;Yong,J.-H.;Paul,J.-C.Simulation ofbubbles.In:Proceedingsofthe 2006 ACM SIGGRAPH/Eurographics symposium on Computer animation,325-333,2006.

[13]Boyd,L.;Bridson,R.MultiFLIP for energetic twophase fluid simulation.ACM Transactions on Graphics Vol.31,No.2,Article No.16,2012.

[14]Hong,J.-M.;Lee,H.-Y.;Yoon,J.-C.;Kim,C.-H. Bubbles alive.ACM Transactions on Graphics Vol.27, No.3,Article No.48,2008.

[15]Mihalef,V.;Metaxas,D.;Sussman,M.Simulation of two-phase flow with sub-scale droplet and bubble effects.Computer Graphics Forum Vol.28,No.2,229-238,2009.

[16]Th¨urey,N.;Sadlo,F.;Schirm,S.;M¨uller-Fischer,M.; Gross,M.Real-time simulations of bubbles and foam within a shallow water framework.In:Proceedings of the 2007 ACM SIGGRAPH/Eurographics symposium on Computer animation,191-198,2007.

[17]M¨uller,M.;Solenthaler,B.;Keiser,R.;Gross,M. Particle-based fluid-fluid interaction.In:Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation,237-244,2005.

[18]Shao,X.;Zhou,Z.;Wu,W.Particle-based simulation ofbubbles in water-solid interaction.Computer Animation and Virtual Worlds Vol.23,No.5,477-487,2012.

[19]Busaryev,O.;Dey,T.K.;Wang,H.;Ren,Z. Animating bubble interactions in a liquid foam.ACM Transactions on Graphics Vol.31,No.4,Article No. 63,2012.

[20]Ihmsen,M.; Bader,J.; Akinci,G.; Teschner, M.Animation ofair bubbles with SPH.In: InternationalConference on Computer Graphics Theory and Applications, 2011. Available at http://cg.informatik.uni-freiburg.de/publications/2011 GRAPPairBubbles.pdf.

[21]Bao,K.;Wu,X.;Zhang,H.;Wu,E.Volume fraction based miscible and immiscible fluid animation. Computer Animation and Virtual Worlds Vol.21,Nos. 3-4,401-410,2010.

[22]Kang,N.;Park,J.;Noh,J.;Shin,S.Y.A hybrid approach to multiple fluid simulation using volume fractions.Computer Graphics Forum Vol.29,No.2, 685-694,2010.

[23]Liu,S.;Liu,Q.;Peng,Q.Realistic simulation of mixing fluids.The Visual Computer Vol.27,No.3,241-248, 2011.

[24]Yu, J.; Turk, G. Reconstructing surfaces of particle-based fluids using anisotropic kernels.ACM Transactions on Graphics Vol.32,No.1,Article No. 5,2013.

Bo Ren received his B.S. and Ph.D. degrees from Tsinghua University in 2010 and 2015, respectively. He is currently a lecturer at Nankai University, China. His research interests include physically based simulation and rendering.

Yuntao Jiang received his B.S.in physics from Tsinghua University in 2015.He is currently a master degree candidate in Department of Computer Science and Technology, Tsinghua University. His research interests include physically based simulation and rendering.

Chenfeng Lireceived theB.Eng. and M.S. degrees from Tsinghua University,China,in 1999 and 2002, respectively,and Ph.D.degree from Swansea University,UK,in 2006.He is currently an associate professor at the Zienkiewicz Centre for Computational Engineering,Swansea University.His research interests include computer graphics,computational mechanics,and computational fluid dynamics.

Ming C. Lin received herB.S., M.S.,and Ph.D.degrees in electrical engineering and computer science from the University of California,Berkeley. She is currently the John R.&Louise S.Parker Distinguished Professor of Computer Science at the University of North Carolina(UNC)at Chapel Hill,and an honorary Chair Professor(Yangtze Scholar) at Tsinghua University in China. She has received several honors and awards,including the IEEE VGTC VR Technical Achievement Award 2010 and 9 best paper awards.She is both Fellow of ACM and IEEE.Her research interests include computer graphics,robotics,and humancomputer interaction,with focuses on physically based modelling,sound rendering,haptics,algorithmic robotics, virtual environments,interactive techniques,geometric computing,and distributed interactive simulation.She has (co-)authored more than 250 refereed scientific publications, co-edited/authored four books.She is a former Editor-in-Chief of IEEE Transactions on Visualization and Computer Graphics(TVCG)during 2011-2014,the current Chair of the IEEE Computer Society(CS)Transactions Operations Committee,and a member of the IEEE CS Board of Governors.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

1CCCE&CS,Nankai University,Tianjin,China.E-mail: rb@nankai.edu.cn().

2DepartmentofComputerScienceandTechnology, Tsinghua University,Beijing,China.E-mail:jiangyt11@ mails.tsinghua.edu.cn.

3College of Engineering,Swansea University,Swansea, UK.E-mail:c.f.li@swansea.ac.uk.

4Department of Computer Science,University of North Carolina at Chapel Hill,Chapel Hill,USA.E-mail: lin@cs.unc.edu.

Manuscript received:2015-08-18;accepted:2015-08-29