Image recoloring using geodesic distance based color harmonization

Xujie Li,Hanli Zhao(),Guizhi Nie,and Hui Huang

©The Author(s)2015.This article is published with open access at Springerlink.com

Image recoloring using geodesic distance based color harmonization

Xujie Li1,Hanli Zhao1(),Guizhi Nie1,and Hui Huang1

©The Author(s)2015.This article is published with open access at Springerlink.com

In this paper,we present a computationally simple yet effective image recoloring method based on color harmonization.Our method permits the user to obtain recolored results interactively by rotating a harmonious template after completing color harmonization.Two main improvements are made in this paper.Firstly,we give a new strategy for finding the most harmonious scheme,in terms of finding the template which best matches the hue distribution of the input image.Secondly,in order to achieve spatially coherent harmonization,geodesic distances are used to move hues lying outside the harmonious sectors to inside them. Experiments show that our approach can produce higher-quality visually pleasing recolored images than existing methods.Moreover,our method is simple and easy to implement,and has good runtime performance.

image editing; colorharmonization; geodesic distance

1 Introduction

Image recoloring is one of the most popular photo editing tasks.Existing work on recolorization can be coarsely divided into scribble-based recolorization and example-based colortransfer[1-4].These methods have been shown to provide satisfactory results,but the quality of recolorization depends heavily on the choice of reference images for examplebased color transfer,while user interaction is tedious and time-consuming in the scribble-based method, limiting its use.

In neither of these approaches is color harmony considered.Color harmonization is a technique used to adjust combinations of colors to meet aesthetic guidelines.Harmonized colors give a pleasing visual effect,and so are necessary for good visual art. In addition,color harmonization is a powerful tool widely used in image and video editing operations, such as color enhancement,image composition,art and design,etc.Therefore,many design tools for producing harmonious color palettes have become popular during the last decade(e.g.,Kuler,Color Scheme Designer,and Colour Lovers)[5].This technique can be applied to enhance the visual harmony of image composition when the foreground and background are notharmonious.Further applications in art and design allow artists and amateurs to create more harmonious visual effects. In this paper we focus on image recoloring based on harmony principles.

The rest of this paper is organized as follows. Section 2 gives a brief review of related work. In Section 3,we introduce the framework of our algorithm.A new strategy for finding the most harmonious scheme is presented and use of geodesic distances is introduced to the color harmonization process.Applications and results are discussed in Section 4.The final section gives conclusions and future work.

2 Related work

Reinhard and his colleagues[6]introduced a color transfer method to recolor images,in which a source image is recolored using the colors of a reference image.Although their technique produces impressive results,finding a reference image with similar appearance is difficult,seriously limitingthe application of the method to color adjustment. Recently,Wang et al.[7,8]introduced a framework which automatically adjusts image color based on semantic user input instead of a reference image. With a single affective word as input,the system does not need any other user interaction,making it easily accessible to amateur users.

Levin et al.[1]proposed a simple yet effective userguided recolorization method in which the user is required to draw a few color scribbles.These provide constraints in a least-squares optimization problem to automatically propagate the scribbled colors.It produces high-quality recolorization.Such methods can achieve good results,but the interaction with the image requires professional skill,making it unsuited to amateur users.

In order to preserve natural shading and highlights to produce realistic recoloring,Carroll et al.[9] and Beigpour and van de Weijer[10]relied on user-assisted intrinsic image decomposition before recolorization.With this decomposition,users can recolor image in terms of illumination and reflectance components respectively.These methods can achieve realistic recoloring results.However,intrinsic image decomposition can be more difficult than recoloring the input image.

During the last decade,increasing focus has been devoted to the area of color harmony[11-13],which may be viewed as color interactions within a spatial framework.Sauvaget et al.[14, 15]introduced a harmonious proportion contrast preservation method to color or recolor images. A serious shortcoming of the algorithm is that colorization or recolorization with exact proportions is a difficult algorithmic problem.

Cohen-Or et al.[16]and Huo and Tan[17] gave color harmony definitions and principles to enhance the color harmony of a given image to make it pleasing to the eye.The challenges of image harmonization are to find the best matching harmonious template,to coherently harmonize the imagewhilekeepingmosthuesintheimage unchanged.Cohen-Or et al.adopt absolute distances to measure the harmony between the hue histogram and the template sectors,weighted by saturation. Then,a graph cut method is used to seek an optimal binary segmentation of the image.Finally, a contraction scheme is employed to shift all the hues of the image.Hues both inside and outside the shaded sectors will contract towards to the centers of the sectors,which changes the harmonious hues and may lead to unnatural results.

In ordertoreducethetimetaken,Sawant and Mitra[18]proposed a histogram splitting method instead of graph cut to reduce segmentation artifacts.A very simple search strategy for the most harmonious scheme uses the sum of image hues in the shaded region of templates.Although their algorithm can operate in real time,it does not account for spatial arrangement of hues.

Tang and colleagues[19]proposed a relative distance based matching function to make more balanced distribution of templates.They solve an optimization problem by minimizing a quadratic cost function based on local smoothness of image hues to recolor images.They also use a two-level graph-cut algorithm[20]to deal with the coherency preservation in image harmonization at region and pixel levels.However,the results rely on the number of image segments,which is difficult to choose properly.They also employ a contraction scheme to shift all hues of the image,so they inherit the limitations of Cohen-Or et al.’s method.

Our work is inspired by the image harmonization algorithms from Cohen-Or et al.[16]and Tang et al.[19].The method proposed in this paper aims to design and derive a more elaborate scheme to match a harmonious template,coherently harmonizing the image while keeping most hues in the image unchanged.

3 Algorithm

In this section,our image recolorization method using geodesic distances is described in detail.An overview of our method is given in Fig.1.The proposed algorithm consists of three steps.First, a search is made for the most harmonious scheme. We do not take saturation into consideration,to make the method more computationally efficient. Nevertheless,our method matches hue distributions of images better than the previous methods.Next, imageharmonization isrealized by reassigning hues outside the harmonious sectors to inside the sectors using geodesic distances.Finally,the user may interactively produce the recolored results by rotating the template after completing color harmonization.

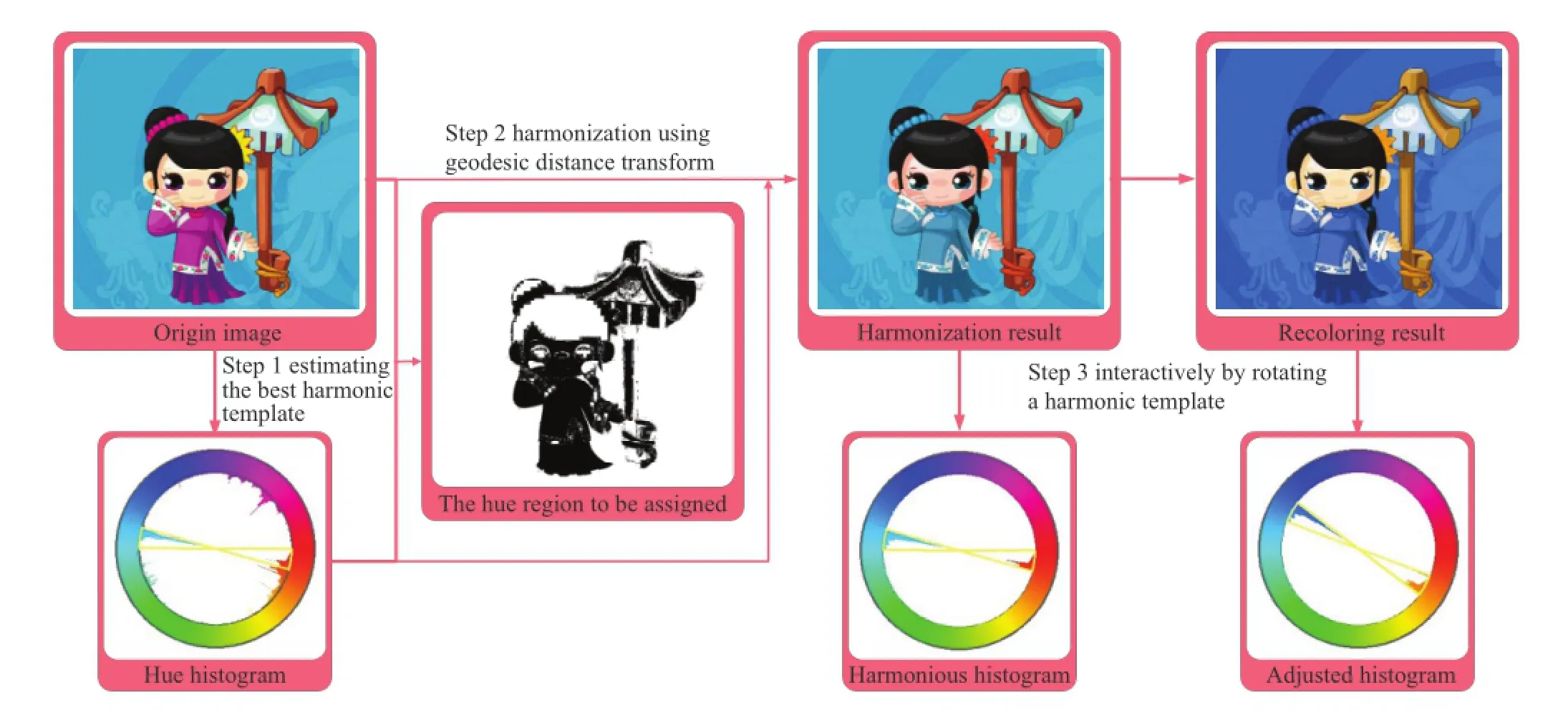
Fig.1 The overall pipeline of our framework.The unknown hues outside the shaded sectors which are denoted in black will be reassigned inside the sectors by using geodesic distances to achieve the spatially coherent harmonization.

3.1 Harmonious schemes

Our research is based on Itten’s model where color harmony is dependent on hue relationships[16].Asshown in Fig.2,eight templates{i,V,L,I,T,Y,X,N}are defined on the hue wheel.The precise sizes and angles of the harmonious template sectors are listed in Table 1. Template N applies to gray-scale images,and is not used in our implementation.

In each template,image hues that fall inside shaded sectors are considered to be harmonious. This is because they are balanced according to human perception.Once the shapes of the templates have been fixed,they may be rotated by an arbitrary angle.

Each harmonious scheme can be defined by(m,θ) where the template is m and its orientation θ(the angle of template rotation);m∈{i,V,L,I,T,Y,X}, θ∈[0,2π).In order to work on the hue wheel of an image,our method changes the color space of the image from RGB to HSV.It then works on the hue channel which is defined from 0°to 360°where 0°corresponds to red.Given an image I,we can define a potential function F(I,Tm,θ)which is usedto measure the harmony between a template and the hue distribution of the image:

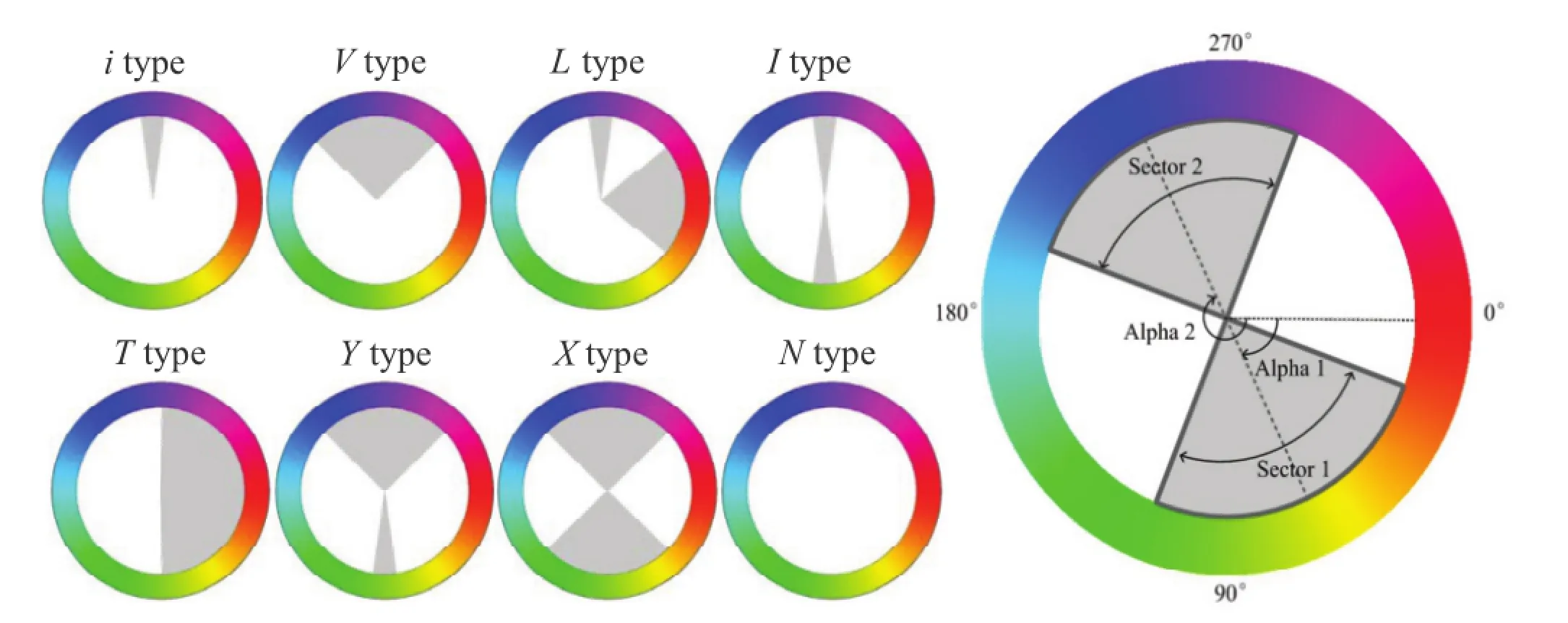
Fig.2 Eight harmonious templates,the definitions of two sectors,and their angles.An image is considered to be harmonious if the entire hue histogram of the image falls inside the shaded sectors for a particular template and orientation.

Table 1 Precise sizes and angles of the harmonious template sectors

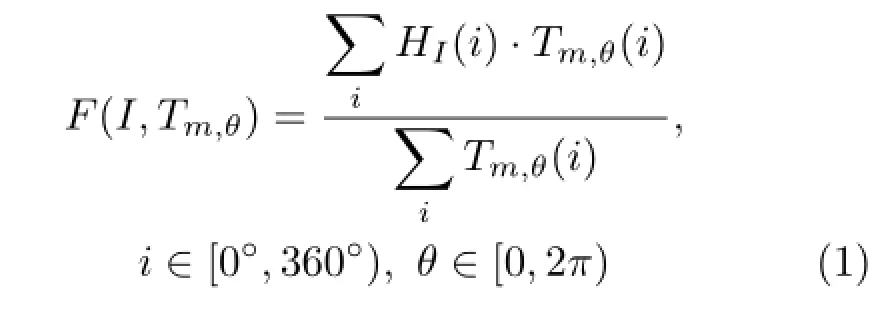
HI(i)is the histogram of the hue channel of an image I.In order to achieve near real-time processing,we do not take saturation into consideration as without it,results are not only comparable,but also our potential function is more computationally efficient. A distribution of a harmonious scheme(m,θ)is defined as

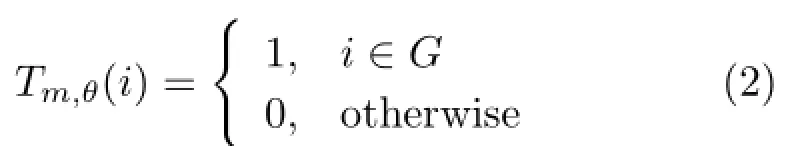
F(I,Tm,θ)represents the means of the hues falling inside the shaded sectors for a particular template and orientation.G denotes the bins falling inside the shaded sectors. The first step is to find an optimal orientation θoby maximizing the value of the potential function for a fixed template m.

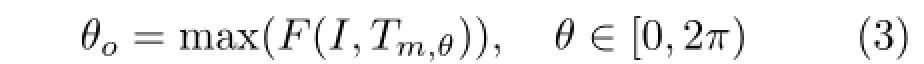
The algorithms from Cohen-Or et al.[16]and Sawant and Mitra[18]just consider absolute distance to measure the similarity between a template and the hue distribution of an image.But their methods ignoretheareainformation.Someharmonious templates which are covered by others may not be selected as the fittest one.Our most harmonious template obeys two rules.Firstly,distribution of selecting harmonious templates should be balanced. Each harmonious scheme should have a probability of being selected as the most harmonious template. Secondly,the number of hues falling inside the shaded sectors of the template should be as high as possible to keep most hues of the image unchanged aftercompleting colorharmonization.In other words,only a few inharmonious hue values should be shifted,to maintain the color theme as much as possible.Therefore,our method tends to favor larger shaded sectors of templates.Our implementation determines the most harmonious template by making pairwise comparisons between the two harmonious templates.We compare the area of the shaded sectors in harmonious template p with the area of the shaded sectors in harmonious template q,using the comparison function below:

If Cp,q＞1,we consider template p to be better than template q,and vice versa.In our implementation,γ is a scale parameter which is critical to measure the degree of harmony in a pairwise comparison of the two templates.Choice of parameter γ is discussed below,and is based on areas of templates.Here,we assume the area of the shaded sectors in template p is larger than in template q.We define parameters α,β as

where α is the ratio of the shaded sector areas of two harmonious templates,and parameter β is the ratio of the mean of the hue histogram in the green sector to the mean of the hue histogram in the red sector (see Fig.3).For simplicity we now define:

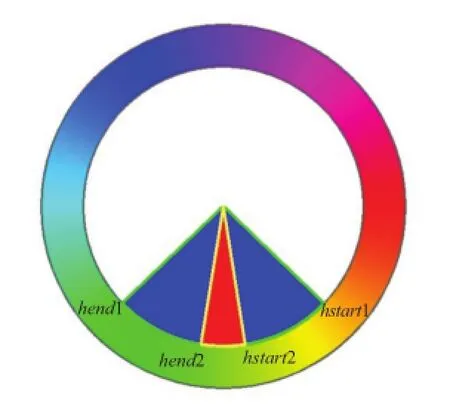
Fig.3 Determining the most harmonious template model.

Here,M and M1respectively calculate the overlap areas of the hue histogram and the shaded sectors of harmonious templates p and q.In the same way, N and N1respectively calculate the areas of shaded sector areas of harmonious templates p and q(see Fig.3).Rewriting Eq.(1)using the above notation, we obtain:

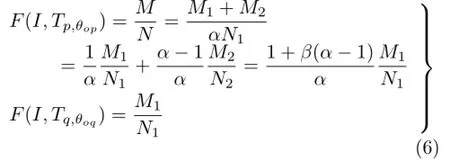
We now introduce the threshold parameter β＇.If β is larger than β＇,we consider template p to be better than template q,and vice versa.In Eq.(4),if Cp,q＞1,template p is considered better than harmonious template q.Combining Eq.(4)with Eq.(6),we can obtain:

When β＇= 0,this gives the absolute distance to measure the similarity between a template and the hue distribution of an image,as in Cohen-Or et al.’s and Sawant and Mitra’s approaches.In our implementation,the threshold parameter β＇is typically set to 10%,to favor larger shaded sectors of templates.Using Eq.(4),we estimate the most harmonious template by pairwise comparison of the two harmonious templates over all possible templates Tm,θo.

Figure 4 shows results of estimating the most harmonious template compared to results from previousmethods.A databaseof100 images was selected to compute the distribution of most harmonious templates as shown in Fig.5.It can be seen that using Cohen-Or et al.’s and Sawant and Mitra’s methods,only T-type and X-type templates can be selected because they both employ absolute distance to measure the similarity of a template and the hue distribution of an image:T-type and X-type templates cover more hues than any other templates. Compared to their methods,our proposed strategy and Tang et al.’s method employ relative distance to measure the harmony of a template and the hue distribution.Our method introduces a new strategy of searching to find the most harmonious schemes which match the hue distribution of the image.The most harmonious scheme is determined by adjusting the threshold parameter β＇.From Fig.5,it can be seen that Tang et al.’s method which employs relative distance has the possibility to select any harmonious scheme.However,their method tends to favor smaller shaded sectors of templates.Our pairwise comparison method has a more balanced distribution of templates than previous methods,as demonstrated in Figs.4-6. Figure 6 shows color harmonization results using different most harmonious templates in comparison with Cohen-Or et al.’s template,where Cohen-Or et al.’s harmonization method is adopted.Only T-type and X-type templates are selected using Cohen-Or et al.’s method,while a more fitting harmonious template can be selected using our method(typically β＇=10%).The limitation of Cohen-Or et al.’s harmonization method is that hues both inside and outside the shaded sectors will contract towards to the center of sectors,which changes the harmonious hues and may lead to unnatural results,as illustrated in Fig.6.

3.2 Color harmonization using geodesic distance transform

Fig.4 Results of estimating the most harmonious template compared with previous methods.(a)Our proposed algorithm;(b) Tang et al.’s algorithm;(c)Cohen-Or et al.’s algorithm;(d)Sawant and Mitra’s algorithm.

Fig.5 A database of 100 images is selected to compute the distribution of most harmonious templates.

Once the most harmonious scheme has been selected, harmony between the colors can be achieved by reassigning the hues outside the shaded sectors to inside the sectors by using geodesic distance. As shown in Fig.1,the unknown hues outside the shaded sectors which are denoted in black are reassigned inside the sectors by using geodesic distance to achieve spatially coherent harmonization. Recently,geodesic distance has been widely used for interactive segmentation and matting in Refs.[21-23].

The hues inside the sectors are kept unchanged. Let Cs,trepresent a curve connecting s to t such that C(0)=s and C(1)=t.The geodesic distance between s and t is defined as follows:

where H is the hue channel of an image. The geodesic distance gives a measurement of how“flat”the flattest curve is between any two points in the hue channel.

For a discrete image I,the geodesic distance between two 8-neighbors of pixels s and t of an image I is

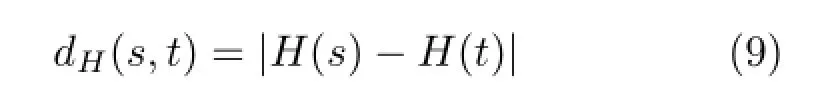
Let the curve C be{p1,···,pm}.Then the distance between pixels p1and pmalong the curve is

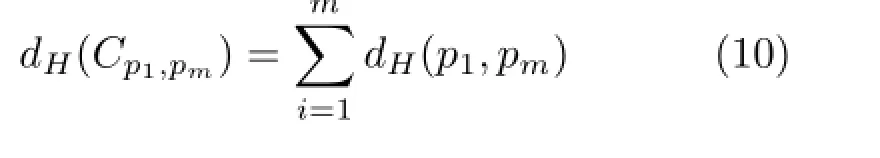
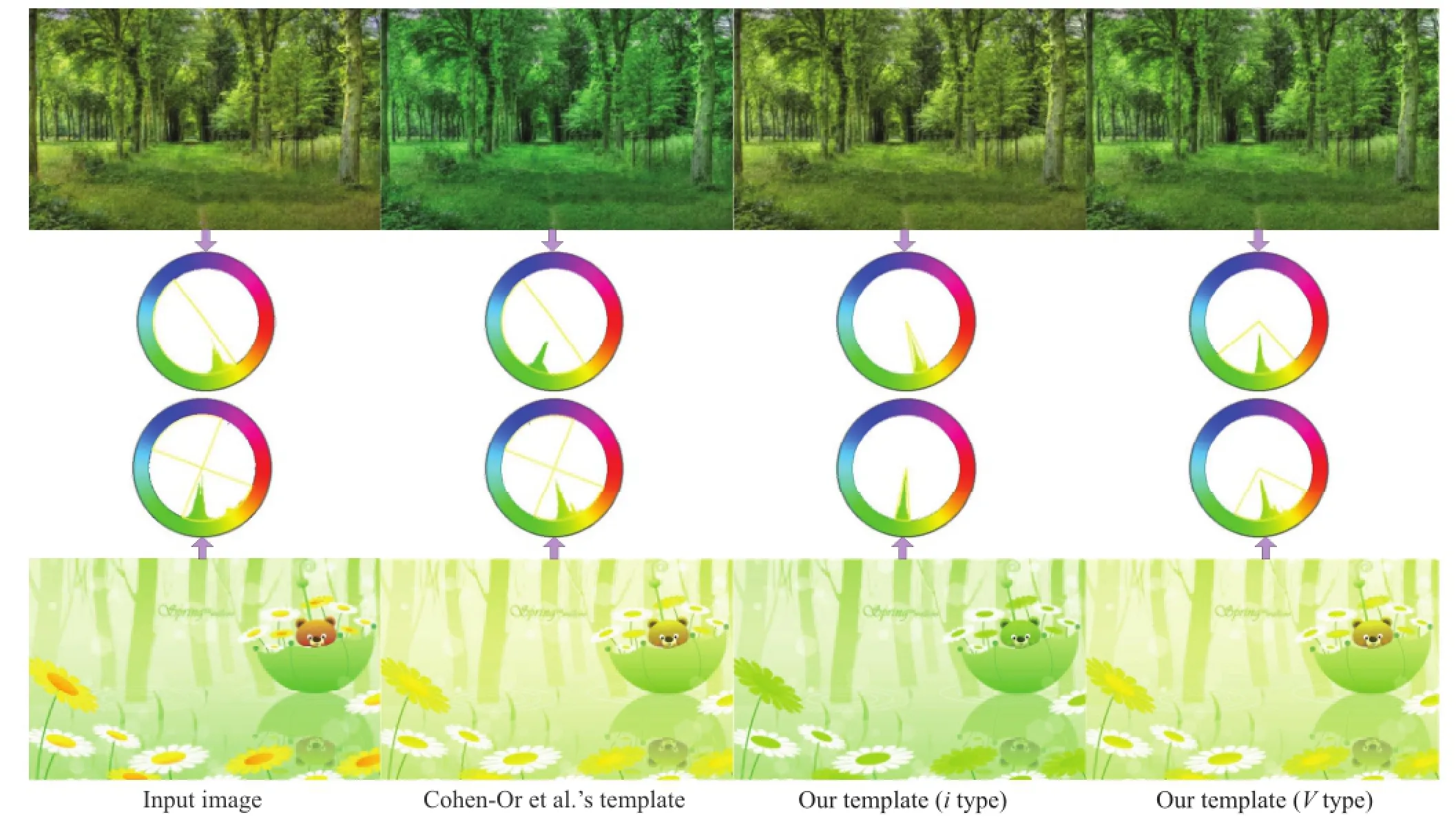
Fig.6 Color harmonization results using different most harmonious templates compared with Cohen-Or et al.’s template.The values of β＇for the i type and V type of our templates are 10%and 3%,respectively.

Given a discrete image I,the geodesic distance between two distant points s and t of an image I is defined as the length of the shortest path joining s and t.

Correspondingly,the hues of the image associated with the harmonious scheme are also divided into two sets.One set denoted ΩN,is composed of hues falling inside the shaded sectors.These hues are considered as known hues.All known hues are unchanged in the harmonization process.The other set,denotedΩU,is composed of the remaining hues falling outside the sectors.These hues are considered as unknowns. All unknown hues in the image I are reassigned inside the sectors by hue blending based on geodesic distance.Thus,image harmonization is realized by reassigning the hues outside the harmonious sectors to inside the sectors.In order to make the reassigned hues fall inside the sectors,every hue in ΩUshould be associated with the most suitable sector.In our implementation,each harmonious template consists of one or two sectors(ΩN=ΩN1+ΩN2).We use a binary segmentation algorithm[21]. The most suitable sector is denoted ΩNS.If the harmonious template consists of one sector,ΩNS= ΩN. If the harmonious template consists of two sectors,the geodesic distances from each hue s in ΩUto the two sectors(ΩN=ΩN1+ΩN2)are

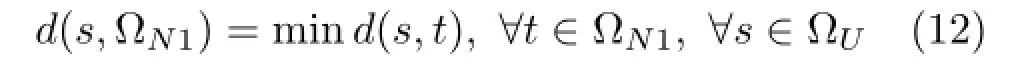
Equation(12)is used to associate every hue inΩUwith the most suitable sector.We can efficiently assign each hue to the most suitable sector with the shorter distance:ΩNS= ΩN1,if d(s,ΩN1)≤d(s,ΩN2).

Finally,the unknown hues in ΩUare obtained by blending the known hues with the closest geodesic distance.

where W(·)is the weighting function:W(d)=d−b. Here,b is the blending factor;typically 1≤ b≤6.From Eq.(13),it can be seen that the unknown hues are computed by hue blending from the known hues which belong to the same sector.Therefore, the unknown hues are transformed so that the hues outside harmonious sectors are mapped inside into one of the harmonious sectors.

Fig.7 Color harmonization results using different harmonious templates(X type is the most harmonious template).

Figure 7 demonstrates that our harmonization method achieves spatially coherent harmonization using different harmonious templates. Note that X type is the most harmonious template and other types of harmonious templates are used to verify the effectiveness of our harmonization method.Color harmonization and template choice on various images are shown in Fig.8.Our method coherently harmonizes images,while keeping most hues of the image unchanged,producing visually pleasingharmoniouscolors.Figure9compares color harmonization results with those of previous methodsusingourmostharmonioustemplate. Cohen-Or et al.’s and Sawant and Mitra’s algorithms adjust the hues outside to fall inside the sectors of the most harmonious template by a contracting method (a linear or nonlinear transformation to contract the value to a certain range).Therefore,the hues inside and outside the shaded sectors will contract towards the centers of sectors,which changes the harmonious hues and may lead to unnatural results.The huesof a red sail are mapped clockwise towards to the centers of sectors using Cohen-Or et al.’s and Sawant Mitra’s algorithms. Our proposed algorithm and Tang et al.’s algorithm reassign hues outside the sectors to inside the sectors while the hues inside the sectors remain unchanged.Figure 9 shows that Cohen-Or et al.’s and Sawant and Mitra’s algorithms strongly contract hues even for colors that originally lie near the middle of harmonious sectors.Unlike their methods,our proposed algorithm and Tang et al.’s algorithm preserve the original colors as much as possible.Tang et al.’s algorithm minimizes the difference between the hue and its neighboring hues. Two spatially disconnected regions of the same red sail are harmonized into different hues.Our method harmonizes the image in a coherent way while keeping most hues of the image unchanged.

Fig.8 Color harmonization and template choice for various images.Top:input images.Bottom:color harmonization results.

Fig.9 Color harmonization results compared with previous methods using our most harmonious template.

We ran our experiments on a graphics workstation with a 2.8GHz Intel Core i5 760 processor and 12GB of memory.The project used Microsoft Visual C++10.0 and the OpenCV 2.4.4 library.From Table 2,it can be seen that our algorithm and Cohen-Or et al.’s algorithm achieve high performance and outperform Tang et al.’s algorithm.Sawant and Mitra’s algorithm can perform real-time color harmonization.Note thatouralgorithm isa CPU-based implementation using a fast marching algorithm [4].Although we currently do not have a GPU implementation of the solver,such an implementation should be possible.Geodesic distance transforms have been shown to achieve realtime performance on GPUs[23,24].We expect a GPU implementation of our image harmonization method should achieve a significant speedup.

4 Applications and results

In our implementation,image recoloring not only considers the color harmony type but also its orientation.Different themes can be expressed by rotating the template.

Figure 10 shows our recolored results andresults of Levin et al.’s popular recoloring method. The first row of Fig.10 shows the process of Levin et al.’s scribble-based recoloring method. Itcan beseen thatLevin etal.’srecoloring method requires considerable user interaction(see Fig.10(b)).Figure 10(c)shows that their method performs poorly when colorizing relatively far from the provided color constraints.More user input, i.e.,additional color scribbles,must be added to improve the quality of the recolored results.Unlike Levin et al.’s method,our method can produce pleasing visual effects without any user scribbles or reference image.As shown in Figs.10(d)-10(f),our method permits the user to obtain recolored results interactively by rotating a harmonious template after completing color harmonization.Figures 10(d)-10(f)demonstrate thatourmethod preserves naturalshading and highlights, and produces realistic recolored results.Traditional methods find it relatively difficult to manipulate small fragments, highly specular and transparent images[10].Various example recolored images with complicated scenes are shown in Figs.11(b)-11(e).The user can interactively produce recolored results by simple manipulation of the color wheel after completing color harmonization.Our method is well suited to recolor complicated scenes as demonstrated in Fig.11.We demonstrate applications of image recoloring using our method.The examples in Fig.12 show that our method can usefully generate harmoniously recolored results in art and design.

Table 2 Performance of color harmonization algorithms,image size 548×730

Fig.10 Recolored results compared with Levin et al.’s popular recoloring method:(a)input images,(b)scribble-images,(c)Levin et al.’s recolored result,(d)-(f)recolored results with color harmonization using our method.

Modifying skin,sky,and glass colors may produce unnatural appearance.In order to preserve the fidelity of such image regions,local image recoloring with color harmonization may be used;we base this on a geodesics-based interactive image segmentation algorithm[21-23].Regions of the image which are marked with black scribbles remain unchanged. Figure 13 shows the process of local image recoloring with color harmonization using our method.

5 Conclusions

In this paper,we have introduced a fast image recoloring algorithm with color harmonization using geodesic distances,whose quality is at least as good as previously reported algorithms.The proposed approach can be used interactively due to itshigh speed. The experimental results show that it can help the user obtain more harmonious recolored effects,even for a user with no professional knowledge.

Fig.11 Recolored images with color harmonization using our method:(a)input images,(b)-(e)recolored results with color harmonization.

In the future,automatic image recoloring for a desired emotion will be considered.It will be convenient for users,especially non-professional users,to recolor an image to meet a desired emotion.

Acknowledgements

This work was supported by the National NaturalScience Foundation ofChina (Grant No.61100146),Zhejiang Provincial Natural Science Foundation of China(Grant Nos. LY15F020019, LQ14F020006,and LQ12F02010),and the Science and Technology Plan Program of Wenzhou,China (Grant Nos.G20130017 and S20100053).

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Levin,A.;Lischinski,D.;Weiss,Y.Colorization using optimization.ACM Transactions on Graphics Vol.23, No.3,689-694,2004.

[2]Liu,X.;Wan,L.;Qu,Y.;Wong,T.-T.;Lin,S.; Leung,C.-S.;Heng,P.-A.Intrinsic colorization.ACM Transactions on Graphics Vol.27,No.5,Article No. 152,2008.

[3]Wang,B.;Yu,Y.;Wong,T.-T.;Chen,C.;Xu,Y.-Q.Data-driven image color theme enhancement.ACM Transactions on Graphics Vol.29,No.6,Article No. 146,2010.

[4]Yatziv,L.;Sapiro,G.Fast image and video colorization using chrominance blending.IEEE Transactions on Image Processing Vol.15,No.5,1120-1129,2006.

[5]Rhyne,T.-M.Applying color theory to digital media and visualization.In:ACM SIGGRAPH 2012 Courses, Article No.1,2012.

[6]Reinhard,E.;Adhikhmin,M.;Gooch,B.;Shirley, P.Color transfer between images.IEEE Computer Graphics and Applications Vol.21,No.5,34-41,2001.

[7]Wang,X.;Jia,J.;Cai,L.Affective image adjustment with a single word.The Visual Computer Vol.29,No. 11,1121-1133,2013.

[8]Wang,X.-H.;Jia,J.;Liao,H.-Y.;Cai,L.-H.Affective image colorization.Journal of Computer Science and Technology Vol.27,No.6,1119-1128,2012.

Fig.12 Applications of image recoloring using our method:(a)input images,(b)-(e)recolored results with color harmonization.

Fig.13 Local image recoloring with color harmonization.Left:image marked with color scribbles by the user.Middle:image area to be recolored.Right:locally recolored results with color harmonization.

[9]Carroll, R.; Ramamoorthi, R.; Agrawala, M. Illumination decomposition for material recoloring with consistent interreflections.ACM Transactions on Graphics Vol.30,No.4,Article No.43,2011.

[10]Beigpour,S.;van de Weijer,J.Object recoloring based on intrinsic image estimation.In:IEEE International Conference on Computer Vision,327-334,2011.

[11]Baveye,Y.;Urban,F.;Chamaret,C.;Demoulin, V.; Hellier, P. Saliency-guided consistent color harmonization.Lecture Notes in Computer Science Vol.7786,105-118,2013.

[12]O’Donovan,P.;Agarwala,A.;Hertzmann,A.Color compatibility from large datasets.ACM Transactions on Graphics Vol.30,No.4,Article No.63,2011.

[13]Seo,S.;Park,Y.;Ostromoukhov,V.Image recoloring using linear template mapping.Multimedia Tools and Applications Vol.64,No.2,293-308,2013.

[14]Sauvaget, C.; Boyer, V.Harmonic colorization using proportion contrast.In: Proceedings of the 7th International Conference on Computer Graphics, Virtual Reality,Visualisation and Interaction in Africa, 63-69,2010.

[15]Sauvaget,C.;Manuel,S.;Vittaut,J.-N.;Suarez, J.;Boyer,V.Segmented images colorization using harmony.In:The Sixth International Conference on Signal-Image Technology and Internet Based Systems, 153-160,2010.

[16]Cohen-Or,D.;Sorkine,O.;Gal,R.;Leyvand,T.; Xu,Y.-Q.Color harmonization.ACM Transactions on Graphics Vol.25,No.3,624-630,2006.

[17]Huo,X.;Tan,J.An improved method for color harmonization.In:The 2nd International Congress on Image and Signal Processing,1-4,2009.

[18]Sawant,N.;Mitra,N.J.Color harmonization for videos.In:The Sixth Indian Conference on Computer Vision,Graphics&Image Processing,576-582,2008.

[19]Tang,Z.;Miao,Z.;Wan,Y.;Wang,Z.Color harmonization for images.JournalofElectronic Imaging Vol.20,No.2,023001,2011.

[20]Tang,Z.;Miao,Z.;Wan,Y.;Jesse,F.F.Colour harmonization for images and videos via two-level graph cut.IET Image Processing Vol.5,No.7,630-643,2011.

[21]Bai,X.;Sapiro,G.Geodesic matting:A framework for fast interactive image and video segmentation and matting.International Journal of Computer Vision Vol.82,No.2,113-132,2009.

[22]Criminisi,A.;Sharp,T.;Blake,A.GeoS:Geodesic imagesegmentation.LectureNotesin Computer Science Vol.5302,99-112,2008.

[23]Criminisi,A.;Sharp,T.;Rother,C.;P’erez,P. Geodesic image and video editing.ACM Transactions on Graphics Vol.29,No.5,Article No.134,2010.

[24]Crane,K.;Weischedel,C.;Wardetzky,M.Geodesics in heat:A new approach to computing distance based on heat flow.ACM Transactions on Graphics Vol.32,No. 5,Article No.152,2013.

Xujie Li is a lecturer at Wenzhou University,China. He received his B.Eng. degree in communication engineering from Ningbo University in 2005 and M.Eng. degree in communications and information systemsfrom Ningbo University in 2008.His research interests include computer graphics,image processing,and GPU parallel computing.

Hanli Zhao is an associate professor at Wenzhou University,China. He received his B.Eng.degree in software engineering from Sichuan University in 2004 and Ph.D.degree in computer science from Zhejiang University in 2009.He is both the members of ACM and CCF.His current research interests include interactive image editing,computer animation, geometric processing,and GPU parallel computing.

Guizhi Nie is a postgraduate student at Wenzhou University,China. She received her B.Eng.degree in computer science from Weifang Science and Technology Collegein 2012. Her research interestsinclude interactive image editing and GPU parallel computing.

Hui Huang is a lecturer at Intelligent Information Systems Institute, Wenzhou University, China. He received his B.Eng.degree in computer science from Wenzhou Normal College in 2005 and M.Eng.degree in computer software and theory from Zhejiang University of Technology in 2008.His research interests include computer graphics and image processing.

Other papers from this open access journal are available at no cost from http://www.springer.com/journal/41095. To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.

1IntelligentInformation SystemsInstitute,Wenzhou University,Wenzhou,China.E-mail:hanlizhao@gmail. com().

Manuscript received:2015-01-09;accepted:2015-04-14