经济短期波动对长期增长的影响——基于面板VAR的实证分析

谢继文，池建宇

（1.重庆交通大学 经济与管理学院，重庆400074；2.中国传媒大学 经济与管理学院，北京100024）

一、引言

经济短期波动和长期增长问题是宏观经济学家关注的两大主要领域。在短期内，经济本身存在一定的波动性，这种波动性一方面来自于经济本身，如企业投资、技术进步等因素；另一方面来自政府的宏观经济政策，如财政政策和货币政策。笔者主要是从以上两个方面研究短期的经济波动对长期增长的影响。不论是资本形成还是政府政策都能在短期内显著影响总产出，除此之外也能影响经济长期的波动性，它们是经济波动的主要来源。

就这一点，学界在是否有必要采取适当的政府干预或者让市场通过自身调节机制保证持续稳定的经济增长方面还存在争议。也就是说，在经济处于衰退期时，应当采取怎样的措施使得经济能够恢复稳定的发展势头。因此，笔者选取的三个变量主要来自以下三个方面，即：资本形成、财政政策和货币政策。

究竟这三个变量是否能够代表资本形成与经济政策的波动性呢？运用经济意义检验的方式，我们发现这三个变量完全能够代替上文所说的三个方面。首先，资本形成总额的波动。资本形成总额指标主要是度量一定时期内固定资产形成总额和存货增加的总量，它主要代表的是经济波动的内因影响，是对本期资本形成效用的主要衡量标准，同时，从经济意义上来看也会对下一期经济增长规模有一定的影响，因此，将其纳入考虑范围。其次，预算赤字的波动。预算赤字这一指标可归结到政府财政政策方面，是将政府财政政策具体量化的重要变量，将其纳入模型，可以探究政府财政政策的变动对于经济增长率是否有显著效果。再次，存贷款规模的波动。存贷款总额这个变量的引入主要是为了量化货币政策，应当采用广义货币作为变量，但是由于本文采用的是省级面板数据，各省广义货币的数据无法得到，因此采用存贷款总额来代替。由于各省的存贷款规模显示了该地区金融市场的活跃状况，通过这个变量可以从一个侧面看出政府的货币政策波动对经济增长率的影响。笔者主要试图回答诸如下列的重要问题：每个变量的波动对于经济增长率是否存在影响？若存在影响，各个变量波动的影响程度又如何？

早期的研究中，Kormendi和Meguire（1985）的研究结果显示，总产出的波动率与平均增长率在各国同一截面上呈正相关关系。Ramey和Ramey（1995）分别使用了92个国家以及其中25个OECD国家的数据验证了平均增长率与增长率的标准差之间的关系。Ramey和Ramey（1995）的控制变量包括投资占GDP之比重、平均人口增长率、初始人力资本和初始人均GDP，使用极大似然估计进行估计。他们发现，使用全样本进行估计，波动性对平均增长率有显著的负向影响，但对OECD国家的数据进行回归的结果却是这种影响为正，但不显著。随后，有大量文献在Ramey和Ramey（1995）的基础上对波动性和平均增长率之间的关系进行经验验证，如Barlevy（2004）、Fatas（2011）得出了相似的结论，即短期波动对增长存在负向影响。也有一些文献的经验分析结果表明，波动性对长期增长的影响是正向的。

近年来，国内涌现了大量针对该主题的理论性和经验性文献。陈昆亭等（2012）发现，中国1978年以前，波动与增长呈负相关关系，1978年之后，二者的关系变为正相关，并建立了一个基于人力资本形成机制的随机增长模型来解释这个现象。李涛（2001）建立了一个反映周期波动的增长模型，将短期波动与长期增长联系在一起。有很多经验性文献使用中国的数据验证了波动性对长期增长的影响，但得出的结论并不相同。王钰（2014）、卢二坡和曾五一（2008）、周达军（2007）的研究支持了Ramey和Ramey（1995）的结论，即短期波动对长期增长的影响为负，但也有文献并不支持这个结论，如卢二坡和王泽填（2007）、池建宇和赵家章（2015）。

笔者主要研究的是宏观经济变量的波动和经济增长率的关系，数据选取的是中国30个省（市、区）（除港、澳、台、西藏外）1980—2013年的年度数据。这个时间段是中国经济从计划经济转向市场经济的主要阶段，也是中国经济真正高速发展的过程。笔者主要通过面板向量自回归（PVAR）模型的构建，借助脉冲响应函数以及方差分解的方法来解释上面所提出的问题，并对中国经济以后的发展提出合理化建议。实证方面，笔者跳出传统对短期波动和长期增长的研究采用“二分法”的桎梏，把这两个主题糅合在一起，探究短期波动对长期经济增长率的影响，试图运用严格的计量方法从经验分析的角度来研究上述问题，采用脉冲响应函数和方差分解的方法分析短期波动和长期增长之间的关系，获得关于短期波动对长期增长的具体冲击程度的描述数据，给出具备说服力的结论，即资本形成和政府经济政策的波动对于长期经济增长率有显著影响。政策方面，笔者运用方差分解的方法重点探究了政府政策的影响力持续时间，得出了政府政策波动短期内能够显著影响总产出。长期内，这种影响力伴随着时间的推移而逐渐减小。因此，政府制定和执行财政政策和货币政策时，不但要考虑其短期的有效性，还要考虑长期的影响力，选择最优的政策幅度，以达到最好的政策效果。

二、数据和方法

（一）变量引入

笔者向模型中引入以下四个变量。

1．经济增长率（growth）——实际GDP增长率，作为模型中的主要研究变量。在前期数据处理时，对实际GDP数据进行取对数处理，因此在离群值处理时，这一变量是正常的。在模型中，该变量为被解释变量，代表长期经济增长的稳定性。

2.资本形成总额的波动（sd_cf）——即资本形成总额占GDP比重的标准差。用标准差来反映变量的波动情况，由于资本形成总额与下一期投资有很强的相关关系（通过经济意义解释），因此，我们估计这个变量的波动对实际经济增长率的影响应该是最大的。

数据处理的过程是：首先计算各省的资本形成总额占GDP的比重，其次，再计算资本形成总额占GDP比重的标准差，需要说明的是，此处的标准差是通过每个省份当年资本形成总额占GDP的比重与该省资本形成总额占GDP比重的平均值之差取绝对值所得出的，虽然不是准确的标准差数据，但是一定程度上也能够反映出资本形成总额占GDP比重各省历年的波动状况，具备一定的解释力。

3.预算赤字的波动（sd_bd）——该变量用预算赤字占GDP比重的标准差表示。这个变量主要是为了检验政府的财政政策对于稳定经济的意义，代表以凯恩斯主义为基础的主流经济学派的观点。

数据处理的过程是：首先通过各省的财政收入与政府支出之差获得各省每年的预算赤字数据，再由预算赤字/GDP获得预算赤字占GDP比重的数据，最终由预算赤字占GDP的比重数据通过软件输出其标准差。

4.存贷总额的波动（sd_cdze）——该变量用存贷规模占GDP比重的标准差表示。由于笔者采用的省级货币供给量数据获得比较困难，因此采用存贷款总额来反映各地的货币发行情况，具备一定的说服力。

数据处理的过程是：首先，将各省的存款规模和贷款规模相加得到存贷款总额，再由存贷款总额/GDP得到存贷款总额占GDP的比重；其次，由存贷款总额占GDP比重数值借由软件输出其标准差。

这四个变量是根据相关的经济周期理论，即凯恩斯主义、货币主义的理论以及真实经济周期理论，来捕捉基本参数对经济波动和经济增长。值得一提的是，后三个变量采用占GDP比重形式，能够很好地克服数据的误差，提高模型的准确性。

（二）数据描述和概况

本文的目的在于研究中国1980—2013年各省主要宏观经济变量波动（短期波动）与其各自实际GDP增长率（长期增长）之间的关系。除特殊说明外，本文数据均来自《新中国60年统计资料汇编》（1949—2008年）和各省统计年鉴（2009—2014年），文中的数据均为原始数据经过单边缩尾处理后所得的结果。本文共采用30个省（区、市）34年的数据（西藏、香港、澳门、台湾除外）。

由于前期的数据收集受到一定的限制，为了能够有效地控制自由度，本研究只选取了四个具有代表性的变量引入模型之中。我们对四个变量的数据做了描述性统计，输出如表1所示。

表1 主要变量的描述性统计

（三）模型构建

笔者采用面板数据向量自回归（PVAR）模型的建构方法，将传统的向量自回归（VAR）方法延伸到处理面板数据（Panel Data）领域，VAR将系统内所有的变量都看成是具备内生性的，而面板数据则是允许未解决的个体差异性存在。

建立PVAR模型需要确定滞后阶数，滞后阶数的确定对于模型十分重要。滞后阶数太小，残差可能存在自相关，并导致参数估计的非一致性；滞后阶数过大，待估参数多，自由度降低严重，直接影响模型参数估计的有效性。面板数据确定滞后阶数的方法一般采用赤池信息准则（AIC）。对数据进行操作后，我们认为滞后两期滞后的效果是最好的，详细输出结果如表2所示。滞后两阶时，在90%的可信度下，AIC、BIC、HQIC均通过，因此，滞后阶数选取两阶即可。

表2 滞后阶数的确定

在下文进行PVAR模型的回归中，又进一步对模型的回归阶数是否正确进行检验，输出结果如表3所示。

表3 PVAR的GMM有效性估计结果

综合上述结果可知，在滞后一阶时，在90%的可信度下，预算赤字波动（sd_bdt-1）不显著；滞后两阶时，在99%的可信度下，除滞后两期的增长率（growtht-2）和存贷总额的波动性（sd_cdzet-2）外，所有变量均能拒绝原假设，均是显著的，故选择滞后两期。这也与上面所进行的滞后阶数检验相符，说明对模型进行面板矩估计（GMM）是有意义的。

结合上文中的变量引入以及滞后阶数检验的结果，我们建构如下模型：

其中zit=（growth，sd_cf，sd_db，sd_cdze）′是基于面板数据的4×1的变量向量，i代表不同的省份，t代表年份，λ1和λ2分别是滞后期不同的变量的系数矩阵，λ0是4×1的各省效应向量（常数项），fi是4×1的年效应向量。如上文所述，growth代表实际GDP的增长率，sd_cf代表资本形成总额的波动，sd_db代表预算赤字的波动，sd_cdze代表存贷款总额的波动，将这四个宏观经济变量纳入同一模型系统，分析各省经济增长速度对不同宏观经济变量波动冲击响应的不同。

在将VAR运用到面板数据中时，我们需要对其施加一定的限制条件，即对于每一个横截面单元而言，其底层结构是相同的。由于这个限制可能在实操中被打破，一种解决方法便是通过引入固定效应的方式允许变量中存在异质性，在模型中通过fi表现出来。而受因变量滞后项的影响导致的fi与自变量的相关性，会使传统用于消除固定效应的“均值差分法”在对系数的估计中产生偏误。因此，笔者使用“前向均值差分法”（Arellano和Bover，1995）来消除固定效应。该方法通过移除前向均值这一转换方式，避免差分项作为工具变量的滞后回归项间的正交，从而达到准确估计模型系统的目的。

三、实证检验结果与分析

（一）PVAR模型及其解释力

根据上文中建立的模型，对面板数据进行向量自回归（VAR）。于是，面板矩估计（GMM）的输出结果如表4所示。

由于本文主要研究的是短期波动对长期经济增长的影响，所以主要观察的数据为表4中的第（1）列，即模型中的各变量滞后一期和滞后二期时对当期经济增长率（growtht）的解释力。

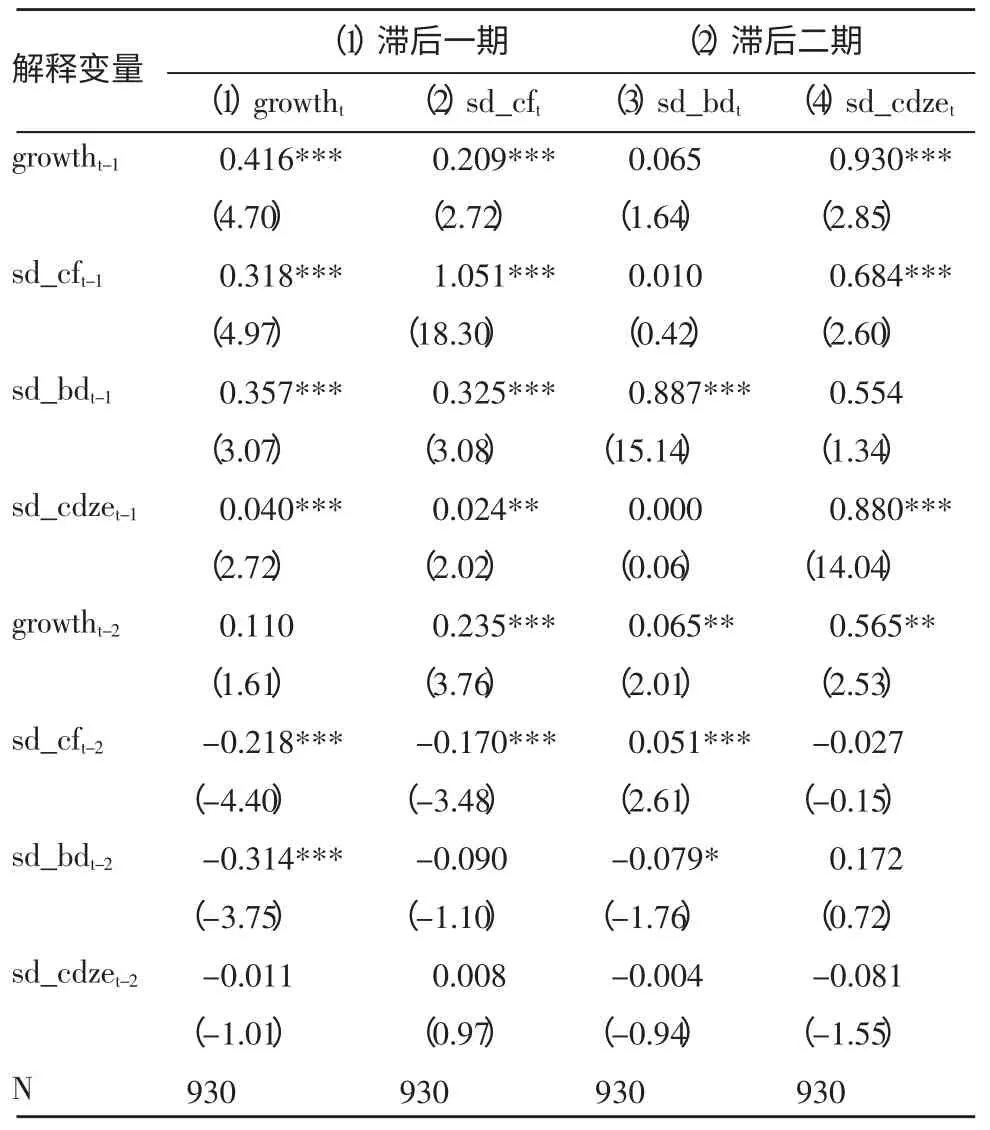
表4 四变量PVAR模型的主要结果

首先，检验模型可行性。由表4可知，在95%的可信度下，模型中的变量除滞后二阶的增长率（growtht-2）和存贷款的波动（sd_cdzet-2）这2个变量的P值大于0.05，其他变量的P值均远远小于0.05。经过笔者的反复验证，这已经是相对最有效的模型，故模型的建立是可行的。

其次，从上面的回归结果可以看出，在growtht作为被解释变量时，sd_cf（资本形成总额的波动）对growtht有影响，滞后一期的sd_cf对growtht有正向影响，其系数是0.318，这样的结果说明上年的资本形成总额的波动对当期的经济增长有正向的影响，即资本形成总额比重的波动越大，对当期经济增长率的拉动就越大。滞后二期的sd_cf对growtht有负影响，其系数是-0.218，说明滞后二期的资本形成总额波动对于经济增长率的影响是反向的；sd_bd（预算赤字的波动）对growtht有影响，滞后一期的sd_bd对growtht有正向影响，其系数为0.357，说明上年的预算赤字的波动会对经济增长率产生正向的影响，并且这个影响还比较大，也就是说预算赤字的波动会对经济增长率产生很大的影响。滞后二期的sd_bd对growtht有负向影响，其系数为-0.314，说明滞后二期的预算赤字的波动对经济增长速度的影响是反向的；sd_cdze（存贷款总额的波动）对growtht有影响，和上述两个变量类似，滞后一期的sd_cdz对经济增长率有正影响，滞后二期的sd_cdze_ratio对经济增长率有负影响，但是就其系数数值而言，分别为0.040和-0.011，这说明滞后一期和二期的sd_cdze对经济增长率（growtht）影响不是很大，至少不如上面两个变量对其影响大。

综上所述，从系数来看，不管是滞后一期还是滞后二期，本文所研究的三个变量波动对长期实际经济增长的影响程度大小依次是：预算赤字〉资本形成〉存贷规模。这样的结果验证了以凯恩斯主义为基本思想的主流观点，即政府的财政政策对稳定经济发展有显著效果，如果当局能够根据现有的实际情况制定合理的财政政策，实现实际经济增长的稳定发展是有可能的。同时，输出结果并没有能够得出货币学派关于货币供给是造成宏观经济不稳定的唯一重要因素的观点。

（二）基于PVAR模型的脉冲响应图

对PVAR单个参数估计值的解释是困难的，要想对PVAR模型做出结论，可以观察系统的脉冲响应函数。脉冲响应函数为我们提供了在其他因素保持不变的情况下，研究一个因素的冲击对其中一个因素的动态影响的方法，它能够比较直观地刻画出变量之间的动态交互作用及效应，并从动态中判断变量间的时滞关系。

正交化脉冲响应函数分析的优势在于它可以通过控制其他宏观经济变量的冲击（令其值为常数），来度量某一特定宏观经济变量的正交化信息（innovation）的响应。

由于式（1）误差项的方差—协方差矩阵可能是非对角矩阵，那么对脉冲响应函数解释的最大困难在于VAR系统的误差项从来都不是完全非相关的，当误差项相关时，他们有一个共同的组成部分，不能被任何特定的变量所识别。处理这一问题笔者采用Cholesky残差的方差—协方差矩阵分解，使误差项正交。该方法的结果一般会受到方程顺序或内生变量顺序的影响。因此变量的设定顺序非常重要，本文的设定变量顺序是growth（经济增长率）、sd_cf（资本形成总额的波动）、sd_bd（预算赤字的波动）、sd_cdze（存贷款总额的波动）。

图1 滞后两阶的四变量脉冲响应图

分析脉冲响应函数还需要建立相应的置信区间，利用GMM估计出的系数以及它们的方差—协方差矩阵随机生成大量系数，并重新计算冲击反应这个过程本文进行了5 000次，蒙特卡洛模拟给出两个标准误差置信区间用于评价冲击的统计显著性，即5%。

图1给出了宏观经济变量波动对实际经济发展的冲击影响。横轴代表追溯期数，这里为6；纵轴表示因变量对各变量的响应大小；中间实线表示响应函数曲线；外侧两条代表两倍标准差的置信区间。需要注意的是，脉冲响应函数是追踪系统对一个内生变量的冲击效果，即假定系统只受一个变量的冲击，不受其他变量的冲击。

图1中第一行分别是经济增长率对其自身的冲击影响，资本形成总额的波动、预算赤字的波动和存贷款总额的波动对经济增长率的冲击影响。由图1可以看出，经济增长率对自身的冲击响应是逐渐开放的。反映财政政策和货币政策的三个指标：资本形成总额的波动、预算赤字波动以及存贷款总额波动情况对经济增长率的冲击均是开放的，但是这其中资本形成总额的波动以及预算赤字的波动两个变量波动情况的冲击在第四期后比其他两个指标的冲击效果更明显，说明经济增长率受资本形成总额波动和预算赤字波动的影响是较大的。

图1中第二、三、四行分别是模型中四个指标波动对资本形成总额的波动、预算赤字的波动和存贷款总额的波动的冲击影响。如果要研究这四个变量之间的相互影响，可以展开说明和论述。但是由于笔者主要研究的是宏观经济变量波动对经济增长率冲击，因此此处不再赘述。

值得一提的是，笔者研究的是短期波动对于长期增长的影响，但是滞后两期四变量脉冲响应图输出结果显示，这个冲击的影响是开放的，而上文中所做回归结果显示，滞后两期时，各变量的影响都变成了负相关关系，但是这并不能说明与脉冲响应图输出结果相悖。因为，脉冲响应图输出的结果是滞后两期变量对于经济增长率冲击的合力效果，虽然滞后二期时，PVAR模型回归结果显示，资本形成总额的波动、预算赤字的波动以及存贷款总额的波动这三个变量对于经济增长率都是反向的影响，且数值都很小，这说明二期之后，资本形成和政府政策对于经济增长率的影响是反向并且微弱的。但是，由于滞后一期时，三个变量波动对经济增长率的冲击太大，滞后二期虽然影响是反向的，但是数值过小，根本无法抵消滞后一期时的正向冲击。以资本形成总额的波动这一变量为例，滞后一期时对经济增长率的正向冲击是0.318，滞后二期时反向冲击是-0.218，两期的合力作用是0.100〉0，因此在脉冲响应图中的反应仍然是在水平线以上。其他两个变量脉冲响应函数位于水平线以上也是由于这个原因，此处将不再赘述。

综上所述，文中面板数据向量自回归模型的输出结果与脉冲响应函数的输出结果是一致的。同时也验证了我们初期的预想，即资本形成总额以及政府政策对于长期经济增长率有显著影响，只是这一影响随着时间逐渐减弱。

（三）方差分解

通过方差分解可以分析影响内生变量的结构冲击的贡献度，进一步度量宏观经济变量的波动对经济增长率冲击作用的构成。输出结果如表5所示。

表5 PVAR方差分解结果

为了与上文脉冲响应图相对应，笔者进行了6个预测期的方差分解。在这里选取其中具备代表性的第3个预测期和第6个预测期的数据进行具体分析。

表5给出了第3个预测期和第6个预测期的方差分解结果。可以看出，虽然经济增长率的变动主要是来源于自身，但是由第3个预测期资本形成总额的波动对经济增长率的影响是1.6%，预算赤字波动的影响是0.7%，存贷总额波动的影响是0.5%；第6个预测期时资本形成总额的波动对经济增长率的影响是1.9%，相较于第3个预测期时，第6个预测期的资本形成总额的波动对于经济增长率的影响较大，这也与上文中脉冲响应图的输出结果相吻合。预算赤字的波动的影响为0.8%，存贷款总额的波动的影响为0.6%。此外，从两个预测期方差分解的数据对比可以看出，伴随着预测期的增加，经济增长率自身波动对其影响力有下降的趋势，这也说明另外三个变量的脉冲影响有上升的趋势。从以上结果可以看出，资本形成总额的波动、预算赤字的波动、存贷款总额的波动这三个变量对于经济增长率的影响不算大，相比而言，资本形成总额的波动以及预算赤字的波动这两个变量对预测经济增长率有较大的贡献率，这一结论也验证了上文在做PVAR模型回归时的结论。

四、结论

改革开放三十多年来，中国经济有了惊人的发展。同时，经济发展过程中也经历了较大的波动。一般来讲，由于宏观经济变量之间的反馈作用的存在，使得研究经济周期模型比较困难。因此，本文选取另一种方式来研究经济周期问题。相较于把焦点放在分析引起经济发展不稳定的原因，笔者主要验证的是与经济增长的影响程度以及影响时效。

笔者用实际GDP的增长率指标衡量我国的经济发展的稳定情况，使用面板数据的向量自回归方法，研究资本形成、财政政策和货币政策的波动对经济发展的稳定性冲击作用。从实证结果看，资本形成、财政政策和货币政策的波动性对经济发展稳定性都有一定的冲击作用。其中，资本形成和财政政策对经济发展的稳定性具有相对较大的影响，货币政策波动对于经济发展的稳定性影响虽然相对较小，但是也有一定的冲击。

首先，短期波动对于长期经济增长率有一定的影响。通过四变量向量自回归模型的建立（PVAR）具体分析了短期和长期时，资本形成、政府财政政策和货币政策的波动对于经济增长率的影响程度。回归结果显示，滞后一期的资本形成、财政政策和货币政策对于经济增长率的影响均为正向影响。此外，就其影响程度而言，财政政策〉货币政策〉资本形成，且三者的数值均不算小，说明影响还是比较显著的。滞后二期时，资本形成、政府财政政策和货币政策对于经济增长率的影响均为反向影响。此外，就其影响程度而言，财政政策〉资本形成〉货币政策，且三者的绝对值数值较滞后一期大幅减少。以上结果说明，短期内，资本形成和经济政策对于经济增长率有显著的正向影响，但是就长期而言，这种影响力会渐渐趋向反向影响，且影响力大幅减小。这便要求经济政策制定者在制定和执行经济政策时，应当综合考虑政策长期与短期的影响，选择最优的政策幅度。

其次，就长期而言，经济增长率对短期波动的脉冲响应函数输出显示，模型中三个变量的冲击是开放的，尽管滞后两阶后，影响方向变成了反向，但是就其实际影响力度而言，远不如滞后一期的正面影响大，所以二者合力效果仍然对经济增长率有较为明显的影响。但是，这个影响力伴随时间的推移将逐渐减弱。

再次，就方差分解的结果来看，对长期经济增长率的波动最主要的来源仍然是内在原因，外在的冲击也对其有一定的影响。这就要求我们在追求稳定经济增长的过程中要把重心放在经济内在结构和内容的调整，同时也不能忽略资本形成和经济政策等外在因素对其的重要影响。

［1］陈昆亭，周炎，龚六堂.短期经济波动如何影响长期增长趋势［J］.经济研究，2012，（1）：42-53.

［2］池建宇，赵家章.短期经济波动如何影响长期增长——来自中国省级层面的证据［J］.北京工商大学学报（社会科学版），2015，（2）：8-17.

［3］李涛.一个反映长周期波动的增长模型［J］.世界经济，2001，（7）：7-15.

［4］卢二坡，曾五一.转型期中国经济短期波动对长期增长影响的实证研究［J］.管理世界，2008，（12）：10-23.

［5］卢二坡，王泽填.短期波动对长期增长的效应——基于省际面板数据的经验证据［J］.统计研究，2007，（6）：32-36.

［6］周达军.我国经济波动对增长的负面效应的实证分析［J］.经济管理，2007，（14）：75-80.

［7］Arellano，M.，and Bover，O.Another Look at the Instrumental Variables Estimation of Error Components Models［J］.Journal of Econometrics，1995，（1）：29-52.

［8］Barlevy，G.The Cost of Business Cycles under Endogenous Growth［J］.American Economic Review，2004，（4）：964-990.

［9］Fatás，A，and Mihov，I.Policy Volatility，Institutions，and Economic Growth［J］.Review of Economics and Statistics，2013，（2）：362-76.

［10］Kormendi，RC，and Meguire，PG.Macroeconomic Determinants of Growth：Cross-country Evidence［J].Journal of Monetary economics，1985，（2）：141-163.

［11］Ramey，G，and Ramey，VA.Cross-Country Evidence on the Link Between Volatility and Growth［J］.American Economic Review，1995，（5）：1138-1151.

［12］Yu，W.How Business Cycle Volatility Affect Economic Growth in China?-An Empirical Study based on GARCH-M Model using the 1952-2012 Data［J］.Advance Journal of Food Science and Technology，2014，（7）：934-940.

［13］丁志帆.转型期中国经济波动的冲击传导机制解析——基于动态随机一般均衡模型的数值模拟分析［J］.山西财经大学学报，2014，（9）：1-13.

［14］池建宇，赵家章.短期经济波动如何影响长期增长？——来自中国省级层面的证据［J］.北京工商大学学报（社会科学版），2015，（2）：8-17.