我国股指期货市场波动的非对称性及其国际比较研究
赖文炜+陈云
摘要:本文在对沪深300和S&P500股指期货的当月连续合约进行展期处理的基础上,基于条件收益分别服从正态、学生t、GED和skewed-t分布的假设,运用GJR GARCH模型对波动非对称性建模,并对模型设定偏误进行严格诊断检验。研究发现:GJR GARCH模型能很好地捕捉股指期货市场波动的非对称性;基于skewed-t分布的波动模型的准确性明显优于其他分布下的相同模型;与S&P500股指期货市场相比,我国股指期货市场波动的非对称性较弱。
关键词:股指期货;非对称性;skewed-t分布
中图分类号:F8309文献标识码:A
一、引言
沪深300股指期货于2010年4月16日落地,开启了我国金融期货的新篇章。经过四年多的发展,沪深300股指期货成交总金额占全国期货市场比例逐年上升,从初期的2657%逐步提高到2012年的4432%,2013年更是达到52%。然而,“87股灾”、“95年巴林银行破产”、“08年法国兴业银行巨亏”等事件表明,高杠杆率意味着股指期货交易存在极高的潜在风险。在当今复杂多变的金融市场环境下,加强股指期货的风险管理以维护金融体系安全更显得尤为迫切和重要。在金融风险的衡量中,波动性是一个被广泛使用的指标,而波动性研究的一个非常重要方面便是关于波动非对称性的研究,这方面研究对于资产定价、投资组合构造与风险头寸的建立都有重要意义。因此,研究我国股指期货市场的波动非对称性有非常重要的现实意义。
国外学者关于金融市场对“利空”消息和“利好”消息的非对称性反应进行了广泛探讨,如Black(1976)、Pagan和Schwert(1990)、Nelson(1991)、Campbell和Hentschel(1992)、Engle和Ng(1993)都发现美国股票市场的波动具有非对称性;Koutmos等(1993)和Booth等(1997)发现在希腊、丹麦、挪威、瑞典、芬兰都存在对“利空”消息和“利好”消息的非对称性反应。大量实证研究得到的一个广为认可的结论是:“利空”消息比“利好”消息对市场的影响更大。
伴随着我国金融市场的迅速发展,学者们进行了大量的市场波动非对称性研究。陈浪南和黄杰鲲(2002)运用GJR GARCH-M模型发现“利好”消息对深圳市场波动的影响要大于“利空”消息。陆蓉和徐龙炳(2004)采用EGARCH模型发现我国股市在牛市和熊市阶段对“利空”和“利好”的非对称性反应存在差异。高辉和赵进文(2007)采用GARCH等模型对上海和伦敦金属期货市场的研究发现,两个市场均存在“利空”消息大于“利好”消息的现象。张青和朱国华(2008)采用EGARCH模型发现我国铜期货市场在牛市和熊市阶段存在显著的波动非对称性,即牛市阶段是“利好”消息大于“利空”消息的影响,而熊市则相反。朱均俊和谢识予(2011)采用MS-TGARCH模型发现我国股市的波动率存在双重不对称性。
尽管学者们已经取得颇丰的研究成果,为我们的研究提供了很好的启发,但目前的研究还存在一些明显不足和值得深入的研究方向:第一,由于我国股指期货市场建立时间不长,对其波动非对称性的研究很少,尚未发现关于我国股指期货市场非对称性与成熟市场的比较研究;第二,很多文献只使用条件正态分布建立GARCH族模型进行分析,没有考虑收益率序列的尖峰厚尾特征。基于以上原因,本文利用沪深300股指期货和S&P500股指期货2010年4月16日-2014年4月17日的交易数据,建立条件收益分别服从正态、学生t、GED和skewed-t分布假设的GJR GARCH模型,系统研究我国股指期货市场的波动非对称性以及这种非对称性与成熟的美国股指期货市场的差异。
二、模型设定与数据说明
(一)模型设定
波动的非对称性检验的理论基础是ARCH模型,而常用的检验模型有EGARCH、VGARCH、GJR GARCH和TGARCH等。Glosten、Jagannathan和Runkle(1993)实证比较了GARCH、EGARCH、GJR GARCH、VGARCH等模型捕捉波动非对称性的能力,发现GJR GARCH模型效果最好。而Engle和Ng(1993)实证发现,在ARCH族模型中,GJR GARCH(1,1)模型是刻画新息(innovation)对收益波动性的非对称影响的最好工具。另一方面,传统的ARCH/GARCH模型均假设所研究的时间序列的条件分布服从正态分布,而实证发现,使用条件正态分布建立ARCH族模型进行残差诊断时,标准化残差的拟合检验通常拒绝条件正态分布的假设。为了刻画收益率序列的尖峰厚尾性质,Bollerslev(1987)和Nelson(1991)分别建议将条件收益分布假设为服从学生t分布和GED分布。孙林和倪卡卡(2013)发现t分布比正态分布和GED分布能更好估计EGARCH模型。为了进一步刻画条件收益分布的非对称性,Giot和Laurent(2003)建议将条件收益假定服从skewed-t分布。王天一和黄卓(2012)的实证也发现,使用skewed-t分布的模型能够很好反映收益率序列的厚尾和偏峰性质。基于以上原因,本文在假设条件收益分别服从正态分布、t分布、GED分布和skewed-t分布情况下,建立四个GJR GARCH模型来刻画信息对收益率波动的非对称性的影响。考虑篇幅,这里只给出其中最复杂的一个模型,即基于条件收益服从skewed-t分布假设的GJR GARCH(1,1)模型:
yt=σtεt,εt~st(0,1,ν,ξ)(1)
σ2t=ω+αy2t-1+βσ2t-1+γI{yt-1<0}y2t-1(2)
其中,ν为自由度(即尾部系数);ξ为偏度系数,它小于(大于)1表示左偏(右偏);γ为杠杆系数,正的γ系数说明“利空”消息比“利好”消息对波动的影响更大;I是反映“利空”和“利好”消息的虚拟变量,如果yt-1<0,则I取1,否则I取0。
(二)数据说明
本文样本数据取自2010年4月16日至2014年4月17日沪深300股指期货和S&P500股指期货的日交易数据,来源于wind金融数据库。需要特别指出的是,这些数据是从当月连续合约获得,且经过1天的展期处理。这样处理的主要原因有二:(1)套保的基本原则是“月份相同或相近”,而股指期货合约月份设计的特定规则加上现货交易时间差异很大,使得期现可能无法完全匹配;(2)远期合约流动性不足,这使得投资者通常会选择流动性比较强的近月合约进行套期保值,当近月合约即将到期时,再向下一个近月合约进行展期。
收益率采用通常用的连续复合形式,即rt=100×ln(pt/pt-1),其中pt为t日收盘价。
三、实证结果与分析
(一)样本统计特征及检验
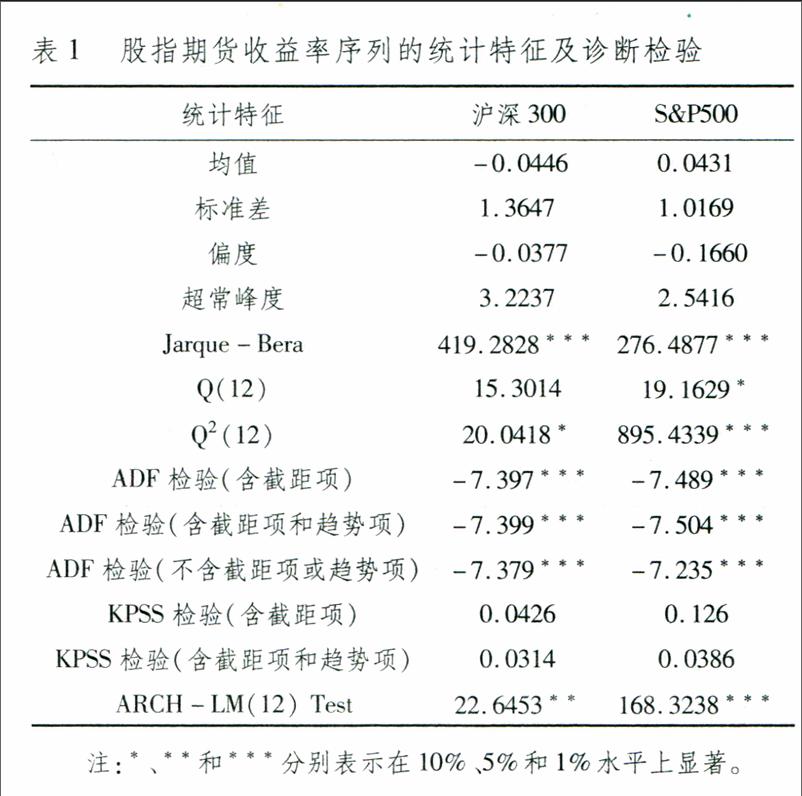
从表1的基本特征及检验结果可以看到,标准差均在15个百分点以内,说明从整体上看两者波动幅度不大;两者的偏度均不为0,且超常峰度都显著大于0,说明这两个序列呈现明显的“尖峰厚尾”特征;J-B统计检验也显著拒绝原假设为正态分布。虽然沪深300股指期货的Q统计量不显著,但其Q2统计量显著,说明存在较为显著的波动持续性。同时,S&P500股指期货的Q统计量和Q2统计量都显著,尤其是后者非常显著,说明其具有非常显著的持续性。ADF检验结果显著拒绝序列存在单位根的原假设;KPSS检验结果表明不能拒绝序列平稳的原假设。所以,可以认为两个序列都是平稳的。而ARCH-LM检验结果强烈拒绝不存在ARCH效应的原假设,表明存在显著的ARCH效应。
(二)模型估计结果与分析
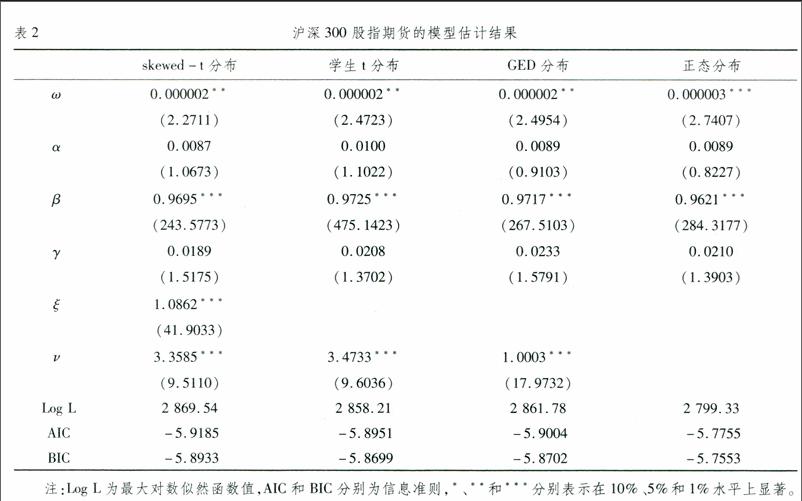
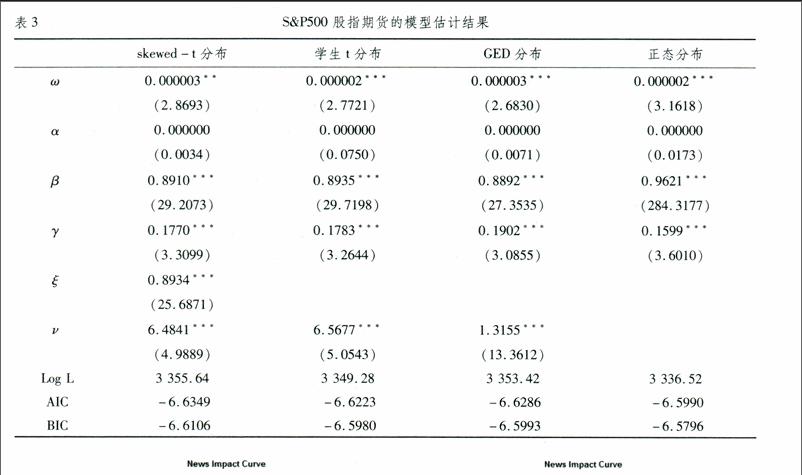
前文统计结果已经表明,两个股指期货时间序列都具有显著的尖峰厚尾特征,与正态分布存在明显差异,且存在显著的ARCH效应。因此,本文对比了skewed-t分布、学生t分布、GED分布和正态分布情况下的GJR GARCH模型估计情况,结果如表2和表3所示。估计结果显示:(1)各模型整体上估计效果均比较理想,这可从对数似然函数值和模型系数的显著性结果上体现出来;(2)无论从对数似然函数值来看,还是根据AIC和BIC信息准则来判断,基于skewed-t分布假设的拟合效果最好,其次是GED分布,接着是t分布,最差的是正态分布;(3)两个序列的GARCH系数即β值都在1%显著性水平下为正,都接近于1,这表明两者波动具有明显波动聚集性;(4)沪深300股指期货的γ系数为正,但统计不显著,而S&P500股指期货的γ系数在1%显著性水平下为正。这说明两种股指期货都存在波动的非对称性,即“利空”消息比“利好”消息对波动的影响更大,只不过前者不够显著,而后者则非常明显。这点还可以从两者的信息冲击曲线(News Impact Curve)的差异更直观地显示出来(见图1)。
考虑文章篇幅,这里只给出了沪深300股指期货和S&P500股指期货在skewed-t分布假设下得到的信息冲击曲线作为参考,它们分别为图1的左图和右图所示。从图形上可以直观地发现,两条信息冲击曲线在冲击小于的0部分均比冲击大于0的部分更为陡峭,这说明负冲击带来的股指期货的波动性的变化更大一些。而且,沪深300股指期货的信息冲击曲线远没有S&P500股指期货的信息冲击曲线不对称。
(三)模型诊断检验
GJR GARCH模型设定是否合适对于最终的结论有很大影响,因此本文采用Engle和Ng(1993)所建议的符号偏误检验(Sign Bias Test)、负程度偏误检验(Negative Size Bias Test)以及正程度偏误检验(Positive Size Bias Test)等方法,来考察条件方差方程的设定是否能够有效反映正(负)收益率的非对称冲击行为。这些检验主要是通过考察是否可以用一些未包含于模型中的变量来预测模型的标准化残差的平方来判断的。如果可以的话,表明条件方程设定有误。检验模型如(3)式所示:
[SX(]t[]σt[SX)]2=κ+c1S-t+c2S-tt-1+c3S+tt-1+ιt(3)
其中,[SX(]t[]σt[SX)]为标准化的残差,ιt为误差项;S-t(S+t)为虚拟变量,分别表示当t-1小于零(大于零)时等于1,否则等于0。如果模型设定合适,则可以进行系数显著性检验,分别为H0:ci=0的原假设(i=1-3),以及H0:c1=c2=c3=0的联合检验(Joint Test)。检验结果如表4和表5所示,四种条件收益分布假设下对应的GJR GARCH模型检验统计量均不显著异于0,说明这些GJR GARCH模型都是可以接受的。
(四)对实证结果的解释
为什么与成熟的S&P500股指期货市场相比,我国股指期货市场的波动非对称性较弱?本文探索性地给出如下三方面原因:
第一,从投资环境来看,相对于巨额的居民储蓄,我国可投资的产品单一。自2007年大牛市后,受股市调整、避险需求增加等因素影响,沪深300股指期货成交总金额占我国整个期货市场的比例逐年上升。然而,目前市场上,缺少类似迷你型指数合约的投资产品以帮助众多中小投资者进行跨期套利、对冲套利,这使得部分投资者面临“利空”消息时,宁愿被“套牢”,也不肯“割肉”。
第二,从投资者结构来看,我国股指期货市场上的投资者按照其对市场的影响力可以分为两类:具有资金和信息优势的机构投资者和数量较多的、资金有限、信息获取和分析能力较弱的中小投资者。目前,沪深300股指期货市场中的机构持仓只占整体持仓30%左右,比国际市场超过50%的比例低很多。机构投资者有较高的信息推断能力,而数量上有优势的个人投资者往往持有短线投机想法,采取顺势而为的交易策略,这些特征使得他们互动形成的“羊群行为”与个人投资者的非理性行为相互抵消,从而导致股指期货市场的杠杆效应不显著。
第三,从市场运作来看,我国股指期货市场还处于发展的初级阶段,各方面制度还不够成熟和完善。就信息披露而言,一般公司都不愿意或尽可能少地提供对其不利的信息,这使得投资者之间的信息更不对称,不利于坏消息传递;而对其有利的信息则会不加限制地任其传播,这样就使得非对称性表现得不明显。
四、结论
本文利用沪深300和S&P500股指期货2010年4月16日至2014年4月17日的交易数据,建立条件收益分别服从正态、学生t、GED和skewed-t分布假设的GJR GARCH模型,系统研究了我国股指期货市场的波动非对称性以及这种非对称性与成熟的美国市场的差异。结果表明:(1)建立的GJR GARCH模型能很好地捕捉股指期货市场的波动非对称性;(2)基于skewed-t分布的波动模型准确性优于其他分布下的相同模型;(3)与成熟的S&P500股指期货市场相比,我国股指期货市场波动的非对称性较弱。
我国股指期货市场波动非对称性不显著,并不意味着它是一个有效的市场;相反,在西方成熟市场,由于杠杆效应、波动反馈效应以及投资者风险规避行为,大多呈现显著的波动非对称性。因此,我们要“三管齐下”,即在大力创新金融品种的同时,还要积极培养和发展股指期货市场机构投资者,优化投资者结构,不断完善信息披露等制度。
参考文献:
[1]Black, F. Studies of Stock Market Volatility Changes[J].Proceedings of the American Statistical Association, Business and Economic Statistics Section, 1976: 177-181.
[2]Bollerslev T. A conditionally heteroskedastic time series model for speculative prices and rates of return[J].The review of economics and statistics, 1987: 542-547.
[3]Engle R F, Ng V K. Measuring and testing the impact of news on volatility[J].The journal of finance, 1993, 48(5): 1749-1778.
[4]Glosten L R, Jagannathan R, Runkle D E. On the relation between the expected value and the volatility of the nominal excess return on stocks[J].The journal of finance, 1993, 48(5): 1779-1801.
[5]Koutmos G, Negakis C, Theodossiou P. Stochastic behaviour of the Athens stock exchange[J].Applied Financial Economics, 1993, 3(2):119-126.
[6]Nelson D B. Conditional heteroskedasticity in asset returns: A new approach[J].Econometrica: Journal of the Econometric Society, 1991:347-370.
[7]Pagan A R, Schwert G W. Alternative models for conditional stock volatility[J].Journal of econometrics, 1990, 45(1): 267-290.
[8]陈浪南, 黄杰鲲.中国股票市场波动非对称性的实证研究[J].金融研究, 2002(5): 67-73.
[9]陆蓉, 徐龙炳. “牛市” 和 “熊市” 对信息的不平衡性反应研究[J].经济研究, 2004(3): 65-72.
[10]孙林, 倪卡卡.国际粮食价格波动非对称性分析——基于 T 分布下 EGARCH 模型[J].南京农业大学学报:社会科学版, 2013(2):10.
[11]王天一,黄卓.高频数据波动率建模——基于厚尾分布的Realized GARCH模型[J].数量经济技术经济研究,2012(5):149-161.
[12]张青, 朱国华.不同市场态势下我国铜期货市场的波动非对称性研究[J].浙江社会科学, 2008(8):15-19.
[13]朱钧钧, 谢识予.中国股市波动率的双重不对称性及其解释——基于 MS-TGARCH 模型的 MCMC 估计和分析[J].金融研究, 2011(3):134-148.
Research on Asymmetry Volatility of China′s Stock Index Futures Market
and International Comparison
LAI Wen-wei1, CHEN Yun2
(1. School of Public Economics and Management, Shanghai University of Finance and Economics,
Shanghai 200433,China;2. Shanghai Key Laboratory of Financial Information Technology
Research, Shanghai 200433, China)
Abstract:In this paper, two continuous price series of CSI300 and S&P500 index future are constructed with rollover. Under the assumption of the conditional return obeying normal, student t, GED and skewed-t distributions, four GJR GARCH models are used to model asymmetry volatility, and Sign Bias Tests are used to test the misspecification of the GJR model. The results show that the GJR models can effectively capture the asymmetry of index futures; the GJR models with skewed-t distribution is superior to the models with other distributions; contrasted with obvious asymmetry of S&P500 index future, CSI300 index future is less asymmetric.
Key words:stock index futures; asymmetry; skewed-t distribution
(责任编辑:张曦)

