算法初步中蕴含的思想方法

刘慧

“算法初步”是新课程标准中的新增内容，旨在使大家体会算法的基本思想以及算法的重要性和有效性，培养条理思考与表达能力，提高逻辑思维能力. 这部分内容，常与函数求值、方程求解、不等式求解、数列求和、统计量计算等问题结合交汇命题. 在算法初步中蕴含了许多常见的数学思想，本文以近几年的高考、统考试题为载体，进行探究说明.

一、函数与方程的思想

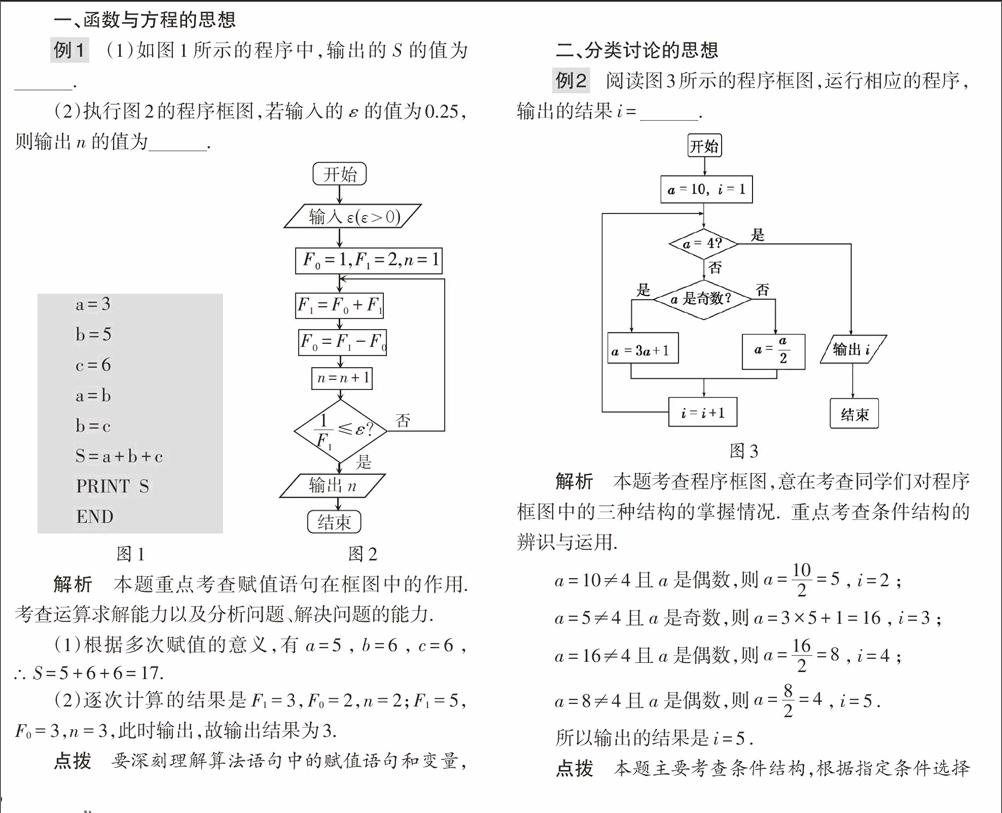
例1 （1）如图1所示的程序中，输出的[S]的值为 .

（2）执行图2的程序框图，若输入的[ε]的值为0.25，则输出[n]的值为 .

解析 本题重点考查赋值语句在框图中的作用. 考查运算求解能力以及分析问题、解决问题的能力.

（1）根据多次赋值的意义，有[a=5]，[b=6]，[c=6]，[∴S=5+6+6=17.]

（2）逐次计算的结果是F1=3，F0=2，n=2；F1=5，F0=3，n=3，此时输出，故输出结果为3.

点拨 要深刻理解算法语句中的赋值语句和变量，必须运用函数的思想去体会. 输入、输出和赋值语句是任何一个算法中必不可少的语句. 在赋值语句中，一定要注意其格式的要求. 将赋值号右边的表达式的值赋给赋值号左边的变量；变量的值始终等于最近一次赋给它的值，先前的值将会被替换. 算法初步中通常会遇到赋值语句与几个常用变量，如计数变量、累加变量和累乘变量. 而明确赋值语句的功能和变量的作用，实质就是要运用函数与方程的思想来理解.

二、分类讨论的思想

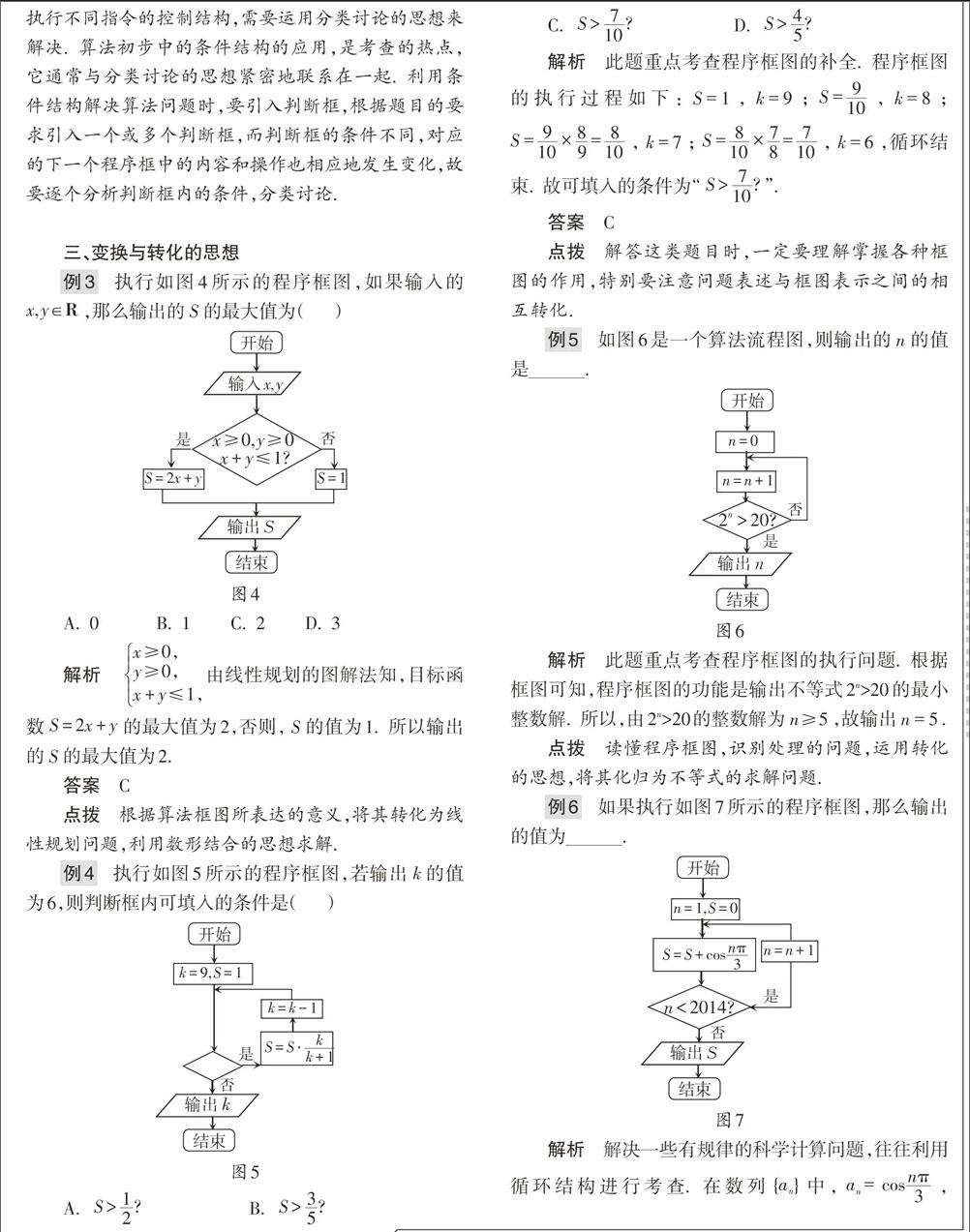
例2 阅读图3所示的程序框图，运行相应的程序，输出的结果[i=] .

解析 本题考查程序框图，意在考查同学们对程序框图中的三种结构的掌握情况. 重点考查条件结构的辨识与运用.

[a=10≠4]且[a]是偶数，则[a=102=5]，[i=2]；

[a=5≠4]且[a]是奇数，则[a=3×5+1=16]，[i=3]；

[a=16≠4]且[a]是偶数，则[a=162=8]，[i=4]；

[a=8≠4]且[a]是偶数，则[a=82=4]，[i=5].

所以输出的结果是[i=5].

点拨 本题主要考查条件结构，根据指定条件选择执行不同指令的控制结构，需要运用分类讨论的思想来解决. 算法初步中的条件结构的应用，是考查的热点，它通常与分类讨论的思想紧密地联系在一起. 利用条件结构解决算法问题时，要引入判断框，根据题目的要求引入一个或多个判断框，而判断框的条件不同，对应的下一个程序框中的内容和操作也相应地发生变化，故要逐个分析判断框内的条件，分类讨论.

三、变换与转化的思想

例3 执行如图4所示的程序框图，如果输入的[x，y∈R]，那么输出的[S]的最大值为（ ）

[开始] [输出[S]] [结束] [输入x，y] [是][否]

图4

A. 0 B. 1 C. 2 D. 3

解析 [x≥0，y≥0，x+y≤1，]由线性规划的图解法知，目标函数[S=2x+y]的最大值为2，否则，[S]的值为1. 所以输出的[S]的最大值为2.

答案 C

点拨 根据算法框图所表达的意义，将其转化为线性规划问题，利用数形结合的思想求解.

例4 执行如图5所示的程序框图，若输出[k]的值为6，则判断框内可填入的条件是（ ）

[开始] [输出[k]] [结束] [是][否]

图5

A. [S>12？] B. [S>35？]

C. [S>710？] D. [S>45？]

解析 此题重点考查程序框图的补全. 程序框图的执行过程如下：[S=1]，[k=9]；[S=910]，[k=8]；[S=910×89=810]，[k=7]；[S=810×78=710]，[k=6]，循环结束. 故可填入的条件为“[S>710？]”.

答案 C

点拨 解答这类题目时，一定要理解掌握各种框图的作用，特别要注意问题表述与框图表示之间的相互转化.

例5 如图6是一个算法流程图，则输出的[n]的值是 .

[开始] [否] [输出[n]] [是] [结束]

图6

解析 此题重点考查程序框图的执行问题. 根据框图可知，程序框图的功能是输出不等式2n>20的最小整数解. 所以，由2n>20的整数解为[n≥5]，故输出[n=5].

点拨 读懂程序框图，识别处理的问题，运用转化的思想，将其化归为不等式的求解问题.

例6 如果执行如图7所示的程序框图，那么输出的值为 .

[开始] [否] [输出[S]] [是] [结束]

图7

解析 解决一些有规律的科学计算问题，往往利用循环结构进行考查. 在数列[{an}]中，[an=cosnπ3]，[a1=12]，[a2=-12]，[a3=-1]，[a4=-12]，[a5=12]，[a6=1]，该数列是以6为周期的数列，且其前6项和等于0. 注意到2014=6×335+4，因此其前2014项和等于335×0+[12]-[12]-1-[12]=[-32]，结合题中的程序框图得知，最后输出的值等于数列[{an}]的前2014项和，即等于[-32].

点拨 读懂算法框图中的循环结构，将其转化为数列求和，三角函数周期等相关的问题. 高考对算法的考查集中在程序框图，特别是带有循环结构的程序框图，主要通过数列求和、求积，统计中的平均数、方差的计算，函数值的计算等带有解决算法的交汇性问题设计试题. 解决的方法是读懂程序框图中的计数变量和累加变量的关系，弄清循环结束的控制条件，通过逐步运算模拟程序的计算方法，明确交汇知识，运用变换与转化的思想找到问题的本质，将其解决.

四、建模的思想

例7 如果执行图8中的程序框图，输入正整数[N][（N≥2）]和实数[a1，a2，…，an]，输出A，B，则（ ）

A. A+B为[a1，a2，…，an]的和

B. 为[a1，a2，…，an]的算术平均数

C. A和B分别是[a1，a2，…，an]中最大的数和最小的数

D. A和B分别是[a1，a2，…，an]中最小的数和最大的数

[是] [结束] [否][是] [输入[N，a1，a2，…，aN]] [x>A] [x>A] [x

图8

解析 对较为复杂的算法框图功能识别的考查. 结合题中程序框图，由当[x>A]时[A=x]可知[A]应为[a1，a2，…，an]中最大的数，由当[x

点拨 此题重点考查算法框图功能的识别，拨开迷雾看清本质. 算法框图功能的识别是算法初步中考查的重点. 为解决此类问题，先弄清变量的初始值；再按照从上到下或从左到右的顺序，依次对每个语句，每个判断框进行读取，在读取判断框时，应注意判断后的条件分别对应着什么样的结果，然后按照对应的结果继续往下读取算法框图，或根据规律总结出该算法框图的功能. 认真分析，联想，建立相关的数学模型. 运用建模的思想不失为解决此类问题的一种好方法.

[练习]

1. 图9是某地区参加2014年高考的学生身高的条形统计图，从左至右的各条形图表示的学生人数依次记为A1，A2，A3，…，A10，如A2表示身高（单位：cm）在[150，155）内的学生人数，图10是图9中统计身高在一定范围内学生人数的一个算法程序框图. 现要统计身高在[160，180）内的学生人数，那么流程图中判断框内整数[k]的值为 .