埋入混凝土的自感知水泥基传感器受力分析

王云洋，薛常喜，丁思齐，张晨宇，韩宝国

（1.大连理工大学 土木工程学院，辽宁 大连 116024；2.青岛北洋建筑设计有限公司，山东 青岛 266000）

自感知水泥基材料是在普通水泥基体材料中添加功能组分制备而成，在外力的作用下，其内部微观结构发生变化，会导致其电学性能发生有规律的变化.因此，可通过测试自感知水泥基材料的电学性能变化来对混凝土结构的应力／应变、裂缝或损伤进行监测［1－2］.由于自感知水泥基材料与混凝土有着天然的相容性和基本一致的寿命，因此适合混凝土结构／构件的健康监测［1－7］.

Han等［8－9］率先开展了自感知镍粉水泥基材料的测试方法、机理、力－电本构关系及其在交通探测等方面的研究，并研制出具有高应力／应变灵敏度的镍粉水泥基传感器（以下简称传感器）［10］.由于镍粉水泥基材料的弹性模量为17.48GPa［11］，混凝土的弹性模量大于20GPa.因此，应用传感器对混凝土结构进行监测，需要分析二者共同受力时的应力／应变状态.

有限元分析已成为研究材料或构件力学性能的有效方法［12］，本文采用有限元软件ANSYS分析了尺寸、电压电极间距和表面粗糙度对埋入式传感器与其周围混凝土应力／应变协调程度的影响，对其制作参数进行了优化，同时分析了它与周围混凝土的受力状态.

1 有限元基本假定及建模

本文依据文献［13］作如下基本假定：（1）传感器各向同性；（2）接触界面通过摩擦传递剪应力；（3）传感器埋入混凝土后，与周围混凝土紧密接触，没有空隙；（4）混凝土处于弹性受力阶段，本构关系为线弹性.

混凝土与传感器均采用SOLID65 实体单元［13－14］，并采用映射方式进行网格划分.在传感器与混凝土的接触区域，将混凝土面定义为目标面并采用TARGE170单元模拟，传感器面定义为接触面并采用CONTA173单元模拟［13］.

混凝土弹性模量取为30GPa，泊松比取为0.2.传感器的弹性模量为17.5GPa，泊松比为0.192［11］.

另外，本文将应变相对差1（Δεrelative1）定义为传感器与其周围混凝土平均应变的比值减1，是对传感器与周围混凝土应变协调程度的衡量指标；应变相对差2（Δεrelative2）定义为传感器与未埋入传感器时相同位置混凝土平均应变的比值减1，是对传感器与未埋入传感器时相同位置混凝土应变协调程度的衡量指标；传感器的平均应变指位于电压电极之间的传感器部分的平均应变；传感器周围混凝土的平均应变指传感器电压电极之间并与传感器接触的混凝土的平均应变；未埋入传感器时相同位置混凝土的平均应变是指未埋入传感器时对应埋入传感器电压电极之间的混凝土的平均应变.应变相对差1，2分别用式（1），（2）进行计算.

2 传感器制作参数的优化

2.1 传感器的尺寸和电压电极间距

2.1.1 传感器尺寸确定

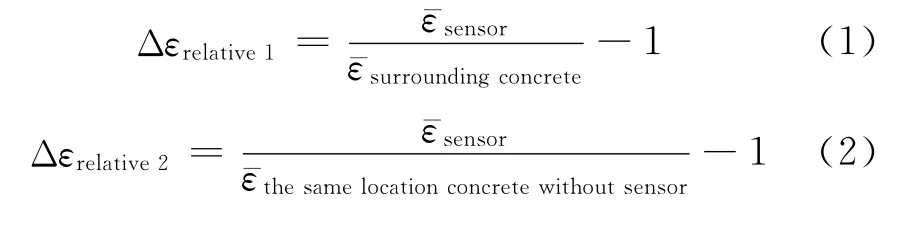
选取边长分别为10，15，20，25，30mm 的正方形截面，每个截面对应5 个高度分别为20，30，40，50，60mm 的传感器.所有传感器均埋在150mm×150mm×300mm 混凝土柱的正中间，并在混凝土柱上表面施加15MPa的均匀压应力（见图1）.如无特别说明，电压电极间距均取5mm.未埋入传感器时相同位置混凝土的平均应力为15MPa，平均应变为500×10－6.图2为不同高度、截面宽度传感器及其周围混凝土的平均应变.由图2（a）可见，当传感器截面宽度一定时，随着高度的增大，传感器的平均应变逐渐减小；当传感器高度一定时，随截面宽度的增大，传感器的平均应变逐渐增大.由图2（b）可见，传感器周围混凝土的平均应变变化规律与传感器的平均应变变化规律相同.

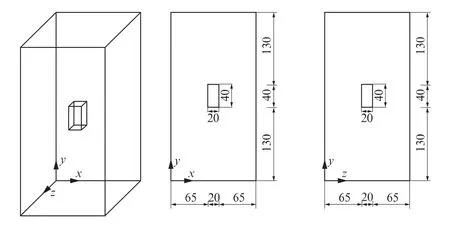
图1 传感器埋入混凝土柱中的示意图Fig.1 Schematic diagram of nickel powder－filled cement－based sensor embedded into concrete column（size：mm）

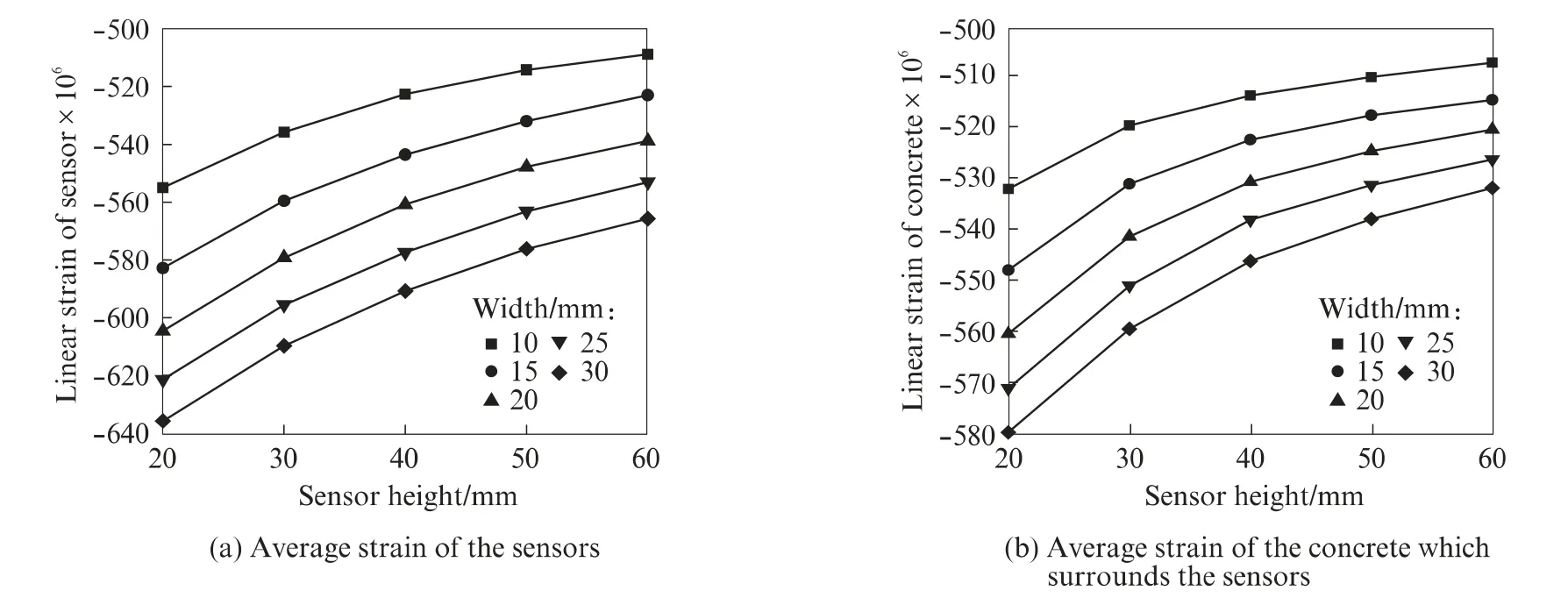
图2 不同尺寸传感器及其周围混凝土的平均应变Fig.2 Average strains of sensors with different sizes and the surrounding concrete

图3 为不同尺寸传感器的应变相对差.由图3（a）可见，当传感器截面宽度一定时，随高度增大，应变相对差1逐渐减小.当传感器高度一定时，随截面宽度增大，应变相对差1逐渐增大.由图3（b）可见，应变相对差2随截面宽度和传感器高度变化的规律与应变相对差1相同.

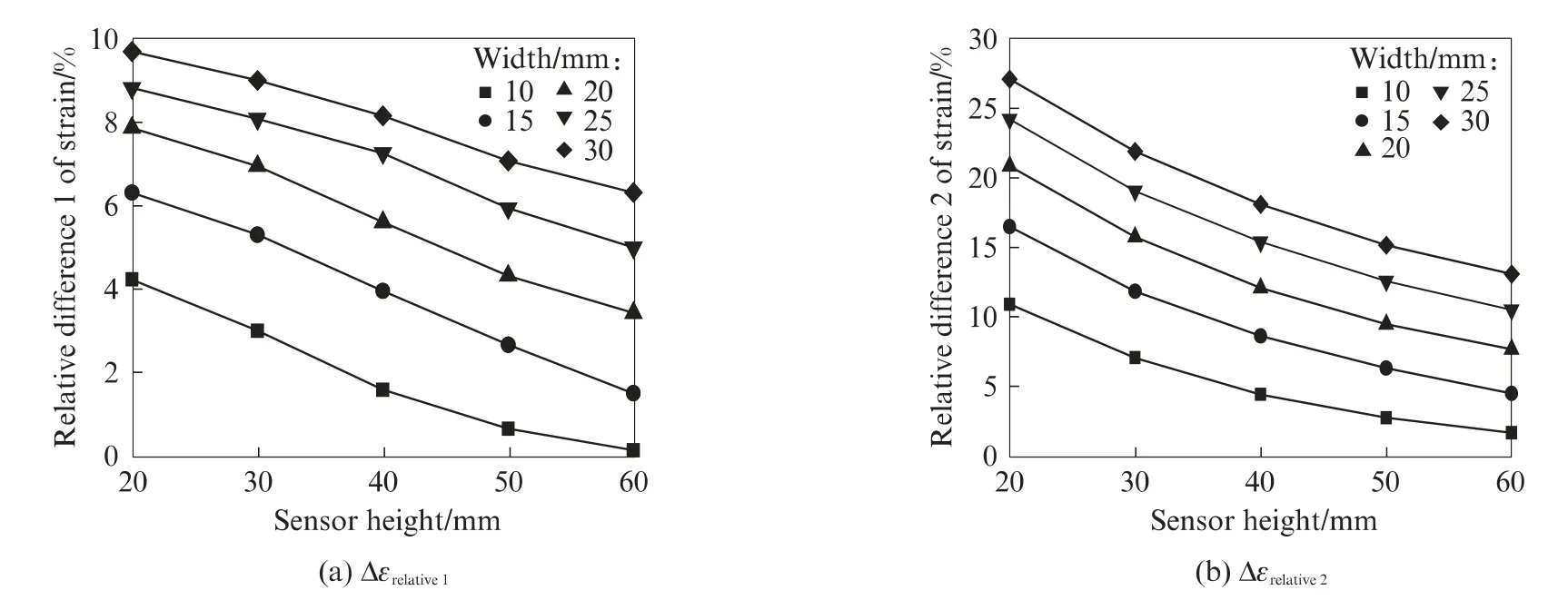
图3 不同尺寸传感器的应变相对差Fig.3 Strain relative differences of sensors with different sizes

根据图2，3，要使传感器的应变相对差较小，应尽量增加传感器的高度，减小其宽度.但随着传感器高宽比增大，传感器的线刚度会减小，且容易产生较大的附加偏心，从而导致脆性破坏.参考GB／T 50081—2002《普通混凝土力学性能试验方法标准》，高宽比取2.尺寸较大的传感器会影响结构／构件的工作性能，而尺寸较小的传感器制作和布设难度会加大.综上所述，传感器的尺寸宜为20mm×20mm×40mm.

2.1.2 传感器的电压电极间距确定

传感器电极为四电极布置.电压电极间距不同，传感器的平均应变也不同.本文选取6种电压电极间距（5，10，15，20，25，30mm）来分析传感器与混凝土的应变协调程度.图4为不同电压电极间距下传感器及其周围混凝土的平均应变.由图4可见，传感器的平均应变略大于其周围混凝土的平均应变，而后者的平均应变略大于未埋入传感器时相同位置的混凝土的平均应变（－500×10－6）；随电压电极间距的减小，传感器和其周围混凝土的平均应变均缓慢减小.

图4 不同电压电极间距下传感器及其周围混凝土的平均应变Fig.4 Average strains of sensors and concrete which surrounds sensors with different electrode separations

图5为不同电压电极间距下的应变相对差.由图5可见，电压电极间距为5mm 时，应变相对差1和2均最小，分别为5.6%，12.2%，随着电压电极间距的增大，应变相对差1先增大后减小，并在电压电极间距为20mm 时达到最大（6.2%）.随着电压电极间距的增大，应变相对差2逐渐增大，并且在电压电极间距为30mm 时达到最大（13.5%）.

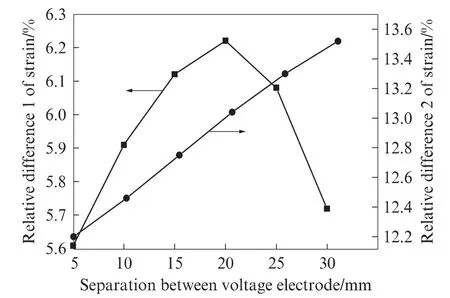
图5 不同电压电极间距下的应变相对差Fig.5 Relative differences of strain of sensors with different electrode separations

根据应变相对差与电压电极间距的关系可知，随着电压电极间距的减小，传感器与周围混凝土应变协调程度越来越好，因此，应选择较小的电压电极间距.由于过小电压电极间距的传感器制作难度较大，所以电压电极间距取5mm 较为合适.

2.2 传感器的表面粗糙度

图6为不同摩擦系数下传感器及其周围混凝土的平均应变.由图6可见，传感器与周围混凝土的应变基本协调，前者略大于后者.随着摩擦系数的增大，传感器的平均应变逐渐减小，其周围混凝土的平均应变缓慢增大，二者的差值越来越小，应变协调程度越来越好.图7为不同摩擦系数下的应变相对差.由图7可知，随着摩擦系数的增大，应变相对差1和2均逐渐减小.

图6 不同摩擦系数下传感器及其周围混凝土的平均应变Fig.6 Average strains of sensors and the surrounding concrete with different friction coefficients

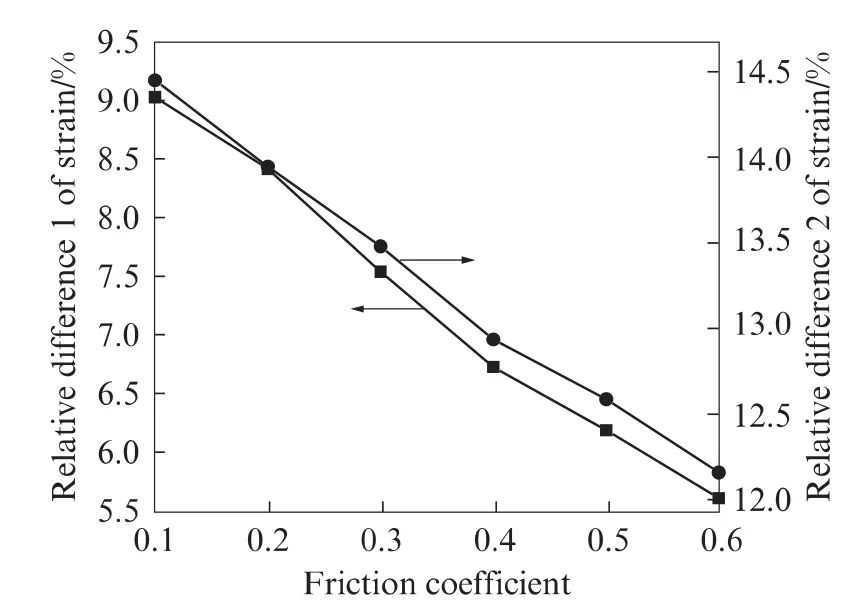
图7 不同摩擦系数下应变相对差Fig.7 Relative differences of strains of sensors with different friction coefficients

由于传感器与混凝土接触界面存在相对滑动趋势，而摩擦力会对相对滑动进行约束，使传感器与周围混凝土的应变更加一致.因此，在制作时宜将其表面进行粗糙化处理，使之与周围混凝土应变更加一致.

3 埋入混凝土中的传感器受力状态分析

3.1 传感器的应力和位移分布

图8为传感器埋入混凝土柱后的应力和位移分布.由图8（a）可见，传感器与周围混凝土的应力相差很大，不协调.由图8（b）可见，传感器与其周围混凝土的位移分布较均匀，表明传感器与周围混凝土的应变基本协调.

3.2 传感器的轴向正应力

图9为传感器轴向正应力σy的分布.由图9（a）可见，传感器轴向正应力分布不均匀，侧面边线和中线处的轴向正应力向传感器1／2高度处靠近时，先增大后减小，截面中心线上的轴向正应力向传感器1／2高度处靠近时，逐渐减小.离传感器1／2高度处越近，轴向正应力分布越均匀.由图9（b）可见，传感器上端面的轴向正应力分布不均匀，从边线中点向中心靠近时，轴向正应力快速增大，并在中心处达到最大值.

3.3 传感器的侧面正应力

图10 为传感器左侧面正应力σx分布.由图10（a）可见，从传感器上下端面向其1／2高度处靠近时，σx逐渐减小，最大σx约为0.55MPa.由图10（b）可见，从传感器侧面z 向中线两端点向中线中点靠近时，σx逐渐减小，最大σx约为0.33MPa.

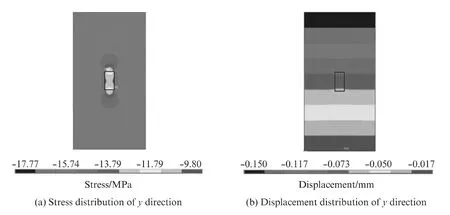
图8 传感器埋入混凝土柱后的应力与位移分布Fig.8 Stress and displacement distribution of sensors embedded into concrete column

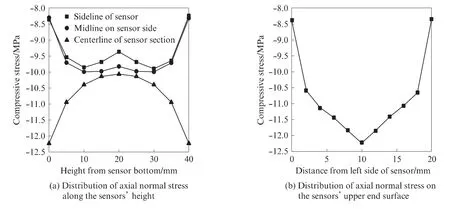
图9 传感器轴向正应力分布Fig.9 Distribution of axial normal stressσyof sensors

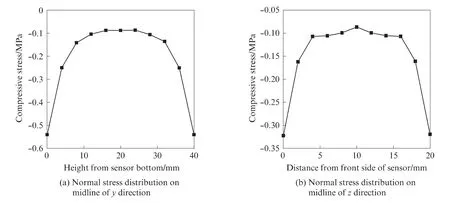
图10 传感器左侧面正应力分布Fig.10 Normal stress distribution on the left side of sensors

3.4 传感器左侧面的剪应力

图11为传感器左侧面y 向中线和边线上的剪应力τxy分布.由图11可见，传感器左侧面上的剪应力均小于0.8MPa，在其1／2高度处为0，当从1／2高度处向两端面靠近时，侧面中线上的剪应力逐渐增大，侧面边线上的剪应力先增大后减小.

由图9～11可见，相对于传感器轴向正应力σy，侧面的正应力和剪应力均较小，可忽略.因此，埋入混凝土的传感器受力状态近似于单轴受力状态.

图11 传感器左侧面剪应力分布Fig.11 Shear stress distribution on the left side of sensors

3.5 传感器的应变分布

图12为传感器的位移分布.由图12可见，传感器截面中心线、侧面边线和侧面中线上的位移分布基本一致.由图12还可以看出，截面中线处应变略大于侧面中线处应变，侧面中线处应变略大于侧面边线处应变.从传感器的上下端向1／2高度处靠近时，应变分布越来越均匀.

由上述分析可知，传感器埋入混凝土柱后，其y向正应力较大且分布不均匀，与周围混凝土不协调，而应变分布与周围混凝土基本协调.这一方面是由于传感器与混凝土弹性模量的差别，而另一方面则是由于传感器与混凝土间存在界面.因此，在实际应用的过程中需对传感器的平均应变进行修正.

图12 传感器的位移分布Fig.12 Displacement distribution of sensors

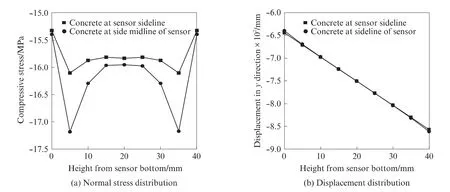
图13 与传感器侧面接触混凝土的正应力和位移分布Fig.13 Normal stress and displacement distribution of concrete contacting with the sensor side

4 传感器侧面混凝土的应力与应变

4.1 传感器侧面混凝土的正应力与应变

图13为与传感器侧面接触混凝土的正应力和位移分布.由图13（a）可见，侧面边线处混凝土的压应力略小于侧面中线处压应力.上下端面处混凝土压应力最小，向传感器1／2高度处靠近时，混凝土压应力先快速增大，然后缓慢减小并趋于稳定.由图13（b）可见，2条直线的斜率基本相等，说明与传感器侧面接触混凝土的应变分布均匀.

4.2 传感器周围混凝土的正应力

图14为传感器周围混凝土的正应力分布.由图14（a）可知，传感器侧面混凝土的正应力随离传感器侧面距离的减小而逐渐增大，最大应力接近16MPa，传感器的埋入使侧面30mm 以内的区域混凝土的正应力增大.由图14（b）可见，传感器上下端面周围混凝土正应力的分布完全一致，随着离传感器端面距离的减小，正应力逐渐减小，最小正应力为11.5MPa，传感器的埋入使其上下端面40mm 以内的区域混凝土的正应力减小.

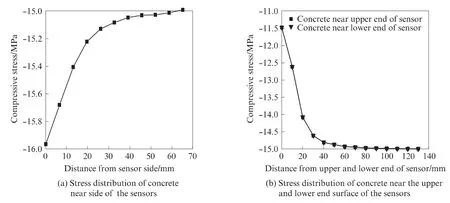
图14 传感器周围混凝土的正应力分布Fig.14 Normal stress distribution of the concrete surrounding sensors

5 结论

（1）传感器合适尺寸为20mm×20mm×40mm，合适电压电极间距为5mm，且其表面应尽量粗糙.

（2）传感器在混凝土中的受力状态近似于单轴受力状态，其应力分布与周围混凝土不协调，而应变分布与周围混凝土基本协调；在实际应用的过程中需对传感器的平均应变进行修正，以保证监测的准确性.

（3）传感器会对周围混凝土的应力分布产生影响，位于其上下端面40mm 以内区域，混凝土的正应力减小，位于其侧面30mm 以内区域，混凝土的正应力有一定程度的增大.

［1］AZHARI F.Cement－based sensors for structural health monitoring［D］.Vancouver：University of British Columbia，2008.

［2］WEN S，CHUNG D D L.Carbon fiber－reinforced cement as a strain－sensing coating［J］.Cement and Concrete Research，2001，31（4）：665－667.

［3］郑立霞，宋显辉，李卓球.机敏混凝土结构变形的自诊断［J］.华中科技大学学报：自然科学版，2004，32（4）：30－31.ZHENG Lixia，SONG Xianhui，LI Zhuoqiu.Self－monitoring of the deformation in smart concrete structures［J］.Huazhong Univ of Sci ＆ Tech：Nature Science，2004，32（4）：30－31.（in Chinese）

［4］HOWSER R N，DHONDE H B，MO Y L.Self－sensing of carbon nanofiber concrete columns subjected to reversed cyclic loading［J］.Smart Materials and Structures，2011，20（8）：1－13.

［5］BAEZA F J，GALAO O，ZORNOZA E，et al.Multifunctional cement composites strain and damage sensors applied on reinforced concrete（RC）structural elements［J］.Materials，2013，6（3）：841－855.

［6］孙明清，张晖，李卓球，等.碳纤维水泥基机敏复合材料的电阻测试研究［J］.功能材料，2004，35（S1）：3352－3355.SUN Mingqing，ZHANG Hui，LI Zhuoqiu，et al.A study on the electrical resistance measurement of carbon fiber reinforced cement based composites［J］.Journal of Functional Materials，2004，35（S1）：3352－3355.（in Chinese）

［7］姚武，徐晶.碳纤维水泥基材料电阻的非线性研究［J］.功能材料，2006，37（4）：632－634.YAO Wu，XU Jing.Nonlinear resistance of carbon fiber reinforced cement based composites［J］.Journal of Functional Materials，2006，37（4）：632－634.（in Chinese）

［8］HAN B G，YU Y，HAN B Z，et al.Development of a wireless stress／strain measurement system integrated with pressuresensitive nickel powder－filled cement－based sensors［J］.Sensors and Actuators A：Physical，2008，147（2）：536－543.

［9］HAN B G，HAN B Z，YU X，et al.Piezoresistive characteristic model of nickel／cement composites based on field emission effect and inter－particle separation［J］.Sensor Letters，2009，7（6）：1044－1050.

［10］HAN B G，HAN B Z，OU J P.Experimental study on use of nickel powder－filled portland cement－based composite for fabrication of piezoresistive sensors with high sensitivity［J］.Sensors and Actuators A：Physical，2009，149（1）：51－55.

［11］HAN B G，ZHANG K，YU X，et al.Nickel particle－based selfsensing pavement for vehicle detection［J］.Measurement，2011，44（9）：1645－1650.

［12］查晓雄，唐家祥.钢管混凝土结构非线性有限元分析中混凝土边界面模型的研究及应用［J］.工程力学，1999，16（6）：29－35.ZHA Xiaoxiong，TANG Jiaxiang.The study and application of concrete bounding surface constitutive relationships to the nonlinear finite element analysis of concrete filled steel tubular structures［J］.Engineering Mechanics，1999，16（6）：29－35.（in Chinese）

［13］薛常喜.自感知镍粉水泥基复合材料及其应用研究［D］.哈尔滨：哈尔滨工业大学，2013.XUE Changxi.Study on self－sensing nickel powder cementbased composites and their application［D］.Harbin：Harbin Institute of Technology，2013.（in Chinese）

［14］陆新征，江见鲸.利用ANSYS Solid65单元分析复杂应力条件下的混凝土结构［J］.建筑结构，2003，33（6）：22－24.LU Xinzheng，JIANG Jianjing.Analysis for concrete structure under complex stress condition with solid 65FEA Element of ANSYS［J］.Building Structure，2003，33（6）：22－24.（in Chinese）