考虑双方风险的定数截尾抽样方案算法优化*

杜旭，王卓健，马涛，沈安慰

（1.空军工程大学航空航天工程学院，西安710038；2.中国飞行试验研究院，西安710089）

考虑双方风险的定数截尾抽样方案算法优化*

杜旭1，王卓健1，马涛2，沈安慰1

（1.空军工程大学航空航天工程学院，西安710038；2.中国飞行试验研究院，西安710089）

在考虑双方风险不同的成败型定数截尾抽样方案设计时，存在尝试法计算复杂、灵活性不高等问题，设计了一种适用性和灵活性较强的优化算法。对抽样方案中累加方程组的等价变形和单调规律分析，采用动态选择步长的方法对已有算法进行优化改进。并针对工程使用中不同风险选择原则难的问题，结合在双方协定的初始风险相等和不等两种情形下，以风险接近为基本原则，构建了风险选择的准则方程。最后传统方法计算结果与该优化算法结果进行对比分析，其结果表明，计算效率得到了较大提升，增强了工程实用性。

定数截尾，优化算法，风险，成败型

0　引言

可靠性鉴定试验是武器装备研制、定型、采办、使用过程中的重要环节，是验证可靠性指标是否达标的主要措施。可靠性鉴定试验中，对于试验结果分为成功、失败两种情况的产品称为成败型产品。在成败型产品验收试验中对于预定的试验次数所得到的成功（失败）次数服从二项分布，在可靠性工程中，电子元器件等设备的可靠性评估试验都是严格服从二项分布的。

基于二项分布的验证方法主要包括定数截尾法、最低可接受值试验法以及序贯截尾试验法。其中最低可接受值法没有考虑双方风险，只考虑了使用方和承制方最低可接受值；序贯截尾试验法判定过程较为复杂，截尾数的选择随机性比较强，不如成败型定数截尾验证法说服力强。目前，成败型定数抽样试验法应用最为广泛。

文献［1］在考虑双方风险的成败型定数截尾抽样模型的基础上，运用证据理论方法，研究了基于研制信息的测试性验证试验方案，并在测试性验证中取得了良好效果。文献［2］将考虑双方风险的成败型定数截尾方法，成功运用到动态分布参数的可靠性鉴定试验方案中。文献［3］针对该抽样方案的使用，提出了查阅标准表和利用计算机搜索求解两种基本方法，但查阅标准表的方法仅仅局限于满足给定鉴别比、双方风险和检验上限值的情况下，降低了工程上的适用范围；而利用计算机搜索求解的方法，只是简单说明了可行性，并没有针对具体算法进行详细说明。文献［4］提出对抽样方案方程组进行等价变形，然后设计相关算法利用计算机搜索求解，但其算法存在相对复杂等问题。因此，深入研究该抽样方案中方程组单调规律，设计出更加灵活、便捷的优化算法，可以增强考虑双方风险的定数截尾抽样方案在工程中的实用性。

本文针对考虑双方风险的定数截尾抽样方案在工程中使用存在的实际问题，在已有算法基础上进行优化设计，有针对性地解决相关问题。提升该抽样方案在工程运用中的灵活性、便捷性和准确性。

1　考虑双方风险的定数截尾抽样方案原理

定数截尾抽样方案基本规则是：假设在某次可靠性鉴定试验中，预定试验次数为n，当试验达到出现事先规定的失败次数f时停止试验，则若f≤c，可靠性指标达标，接受；若f>c，不合格，不接受。

在该抽样方案中对于生产方和使用方协商确定的不可靠度R0和R1以及风险值α、β来说，这些参数满足以下关系［5］：

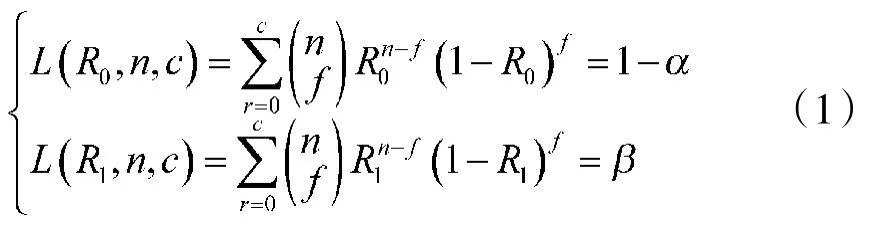
式（1）中，相关参数意义如下：

①检验下限R1

不可接收的可靠度R1，统计试验方案以高概率拒收真值接近的产品，其值可取设计定型最低可接受值R1；

②检验上限R0

可接受的可靠度R0，统计试验方案以高概率接收真值接近的R0产品，其值应小于预计值；

③鉴别比DR

二项分布统计试验方案的鉴别比为：DR=（1-R1）/（1-R0）；

④生产方的风险α

当待命成功率真值等于其检验上限R0时设备被拒收的概率；

⑤使用方风险β

当待命成功率真值等于其检验下限R1时设备被接受的概率。

设计可靠性鉴定试验方案时，根据生产方、使用方协商确定DR，R0，α，β值，求解式（1）中未知数n和c，即可确定抽样方案中的试验次数n和成败判定数c。为方便使用，GB5080.5［6］（ICE605-5）提供了定数试验方案表，标准表中给定了取某些固定值、DR取1.5、1.75、2.00、3.00、α=β分别取5%、10%、20%、30%时的试验次数n和成败判定数c。

李晓阳等［4］通过数学推导对式（1）进行了等价变形，等价后的方程组为：

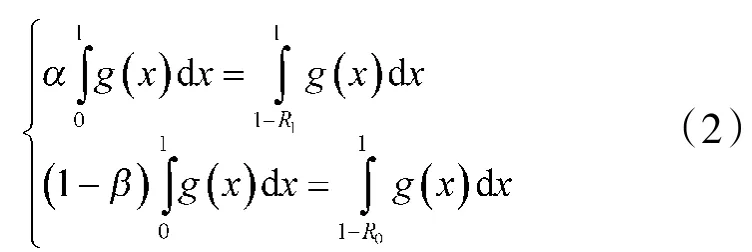
并在等价变形的基础上，初步研究了式（2）的单调规律，提供了求解的基本思路，但其算法在工程应用中存在不够灵活、计算速度慢等问题。

2　算法优化设计

对于一个没有整数解，又包含高次积分的式（2），直接求解出精确解几乎是难以实现的。

通过对GB5080.5［6］对比分析和对等价方程组数学规律研究的基础上可以发现，该等价方程组具有单调性：当检验上限R0、双方风险α=β不变时，试验数n、判定数c随着鉴别比DR增大而减少；当检验上限R0、鉴别比DR时，试验数n、判定数c随着双方风险α=β增大而减少；当鉴别比DR、双方风险α=β不变时，试验数n、判定数c随着检验上限R0增大而减少。方程组的单调性同时适用于每一个方程。等价方程组式（2）数学规律的研究，是优化算法设计的第一步。

2.1优化算法基本思路

由于在工程实际的验证试验中只需要整数解，式（2）的精确解对于可靠性鉴定没有现实意义。因此，可采用试探方法先求解出满足方程租未知数n和c取值范围，再根据工程需要确定出整数解。

采用逐点试探的方法首先面临着步长的选择，如果对n和f只进行步长为整数的搜索，很难获取满意解；如果步长选择较小，在增加计算次数的同时也增加了积分难度，会大幅降低计算效率。因此，本文根据计算需要动态确定步长的方法，可最大限度减少计算次数。

在成败型抽样方案中n相对c是大值，如果先对n进行遍历的话，比如n=100和c=10，那么遍历的次数就是10100；先对c进行遍历，再对n进行搜索，那么搜索的次数就是10010。其中前者搜索次数是后者的1080倍，因此，采用先对c进行遍历，后对n进行一维搜索方法。

根据等价方程组的单调性，可以借助标准表GB5080.5，大致框定抽样方案中n和c的最大取值nmax和cmax。其目的是避免在对n和c进行遍历时的盲目性。

2.2求解判定数c

判定数c取值从1开始进行整数遍历到cmax，首先求解不同c值下方程Ⅰ、Ⅱ的n取值范围，再根据方程Ⅰ、Ⅱ的n取值范围之差来确定式（2）中c的取值。（便于说明规定式（2）中第1个方程用方程Ⅰ表示，第2个方程用Ⅱ表示）。本文拟分5步来阐述求解判定数c的基本思路。

Step 1初步确定c取整数值时，式（1）、式（2）中n的取值范围。

给定n的初值1，计算式（1）左右两边的积分结果，然后比较二者大小，用旗帜变量f记录下它们的比较结果。f（c，n）=1代表等式左边的积分结果大于等式右边，f（c，n）=-1代表等式左边小于等式右边，而f（c，n）=0代表它们相等，此时的n即为方程的解。如果f（c，n）≠0，那么对n=n+1进行重复计算，如果f（c，n）≠f（c，n-1），则n取值就在n-1～n之间。记录的方程Ⅰ不同c值下的n取值范围（nc，1-1～nc，1），同理第Ⅱ个方程n的取值范围（nc，2-1～nc，2）。

Step 2缩小每个方程n的取值范围。

要满足确定c值的需要，必须缩小n的取值，在Step 1中通过缩小步长到0.031 25，也可达到缩小n取值范围的目的，但相同情况下相对该优化算法计算次数增加了cmax倍，因此该优化算法注重提升计算效率。式（1）缩小n取值范围具体步骤如下：

①A=nc，1-1，B=nc，1，C=（A+B）/2；

②根据前文旗帜变量定义方法，分别求出f（c，A）、f（c，B）、f（c，C）；

③当f（c，A）≠0，f（c，B）≠0，f（c，C）≠0，如果f（c，A）≠f（c，B），则B=C、C=（A+B）/2；如果f（c，B）≠f（c，C），则A=C、C=（A+B）/2；

④重复a、b、c步骤5次，则n值介于（A，B）之间；

⑤令nnc，1=B，则方程Ⅰ在c值下n的取值范围为nnc，1-0.032 15～nnc，1。

运用以上5个步骤可以将不同值下方程Ⅰ、Ⅱ的n取值范围缩小。

Step 3确定nnc，1和nnc，2之差最小值时的c0值和对应的差值cha1。

式（1）、式（2）是同属于等价方程组式（2）的两个独立方程，因此，不同c值下两个方程n取值越接近，对应的c值才有可能是方程组的解。通过构造准则方程cha1=Min（chac，1）=Min（|nnc，1-nnc，2|），求解cha1，并令取cha1值下的c取值为c0。

Step 4求解c取c0+0.001下的两个方程n取值之差cha2。

通过步骤Step 1、Step 2、Step 3，计算出c0+0.001二者n取值范围之差cha2。

Step 5通过对比cha1和cha2确定c值。

通过对比cha1和cha2取值大小确定c的准则如下：

式中：cha1＜cha2表明n取值范围之差在c0处递增；cha1＞cha2相反则能够表明在c0处递减。

2.3确定试验样次数n

明确判定数c之后，接着就是要确定试验次数n，试验次数不仅仅关系着试验进度、成本，同时与双方实际风险直接关联，双方风险选择有许多原则可以遵循，不同的原则，将决定不同的试验次数n。

基于风险接近原则的试验次数确定方法，其实就是一种相对公平原则。在制定合同阶段，双方在权衡各方面因素基础上，对风险进行协定，因而在可靠性鉴定试验中，尽量保证双方的实际风险接近协定风险也是可以被双方广泛认同的。

可靠性鉴定试验中，双方协定的初始风险存在相等、不等两种情形，不同情形下确定试验次数时，会存在不同的问题。为了便于解决该问题，通过构建准则方程，使风险选择问题抽象化。准则方程的构造方法具体如下：

1）双方协定风险α0=β0时，构建准则方程：

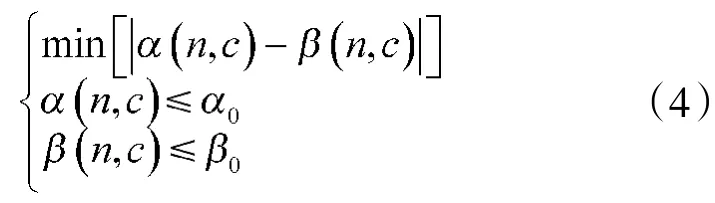
图1　优化算法计算流程图

该准则方程构建的基础是实际风险均小于协定风险，并且满足双方实际风险差值的绝对值最小。

2）双方协定风险不等时：

①协定风险α0＞β0，构建准则方程

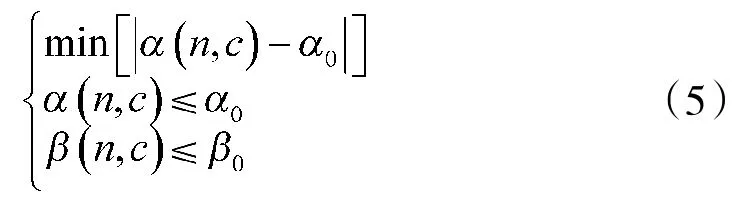
②双方协定风险α0＜β0，构建准则方程

准则方程式（5）、式（6）构建的基础是实际风险均小于双方协定风险，并且试验次数最少、试验成本最低，鉴定试验进度最快。

3　实例计算分析

某型航空装备，设计初期合同中规定可靠度指标R0=0.95，鉴别比DR=2.5，经协定生产方和使用方风险分别为α0=0.25、β0=0.15。

根据设计的优化算法，首先大致框定出nmax=187和cmax=14，并计算不同值下方程1、2的n取值范围；并可快速计算出cha1=1.687 5以及其对应的c0=2；当取c=c0+0.001=2.001时cha2=1.665 5，由式（3）判定c=c0+1=3；由于双方协定风险α0＞β0，故选用准则方程式（5），编程求解出试验次数n=47。因此，基于该优化算法确定抽样方案为（47，3）。

为验证算法的有效性，可通过传统方法计算结果与该优化算法结果进行对比分析。根据已知的（n，c），通过方程组式（2）反算出双方实际风险。选取具有代表性的抽样方案，计算出双方实际风险如表1所示。

表1　某些抽样方案下双方实际风险

由表1可以看出抽样方案试验次数由小到大，总是一个α增大β减少的过程，根据双方风险均小于协定风险原则，只有当“判定数”c=3才能满足该要求。对于使用方来说，判定数一定试验次数越大，那么“取伪”的概率就越小，而对生产方“弃真”的概率就越大。因而在样本量选择范围内，最小试验次数n=47已经满足使用方的需要，并且样本量小会对承制方有利，同时也减少了试验成本，因此，例1中应取n=47。

通过实例说明了本文设计的优化算法可以方便、快速确定出试验次数、判定数。并在大量的实例计算中验证了该算法的有效性。

4　结束语

本文根据考虑双方风险的定数截尾抽样方案，在可靠性鉴定试验中的实际情况，以抽样方案设计科学、合理，计算快速、准确、使用简单、便捷为基本原则，进行算法优化设计，可在工程上实际应用，主要解决的问题有：

①增强了成败型抽样方案在工程应用中的范围。针对国标中没有给定的R0、DR、α、β提供适用性强的算法；弥补了双方初始风险不等时，该抽样方案的使用受到限制的局限性；

②本文设计的优化算法，相对已有算法通过动态改变步长的方法，可最大限度减少计算的次数，提高计算效率，增强了该抽样方案在工程应用中的便捷性；

③针对工程使用中不同风险选择原则难的问题，提出了通过构建准则方程的方法，解决了算法设计中样本量选择技术难点；同时考虑了在满足风险接近原则的前提下，可降低样本量、节省试验成本、加快试验进度。

［1］Chang C H，Yang J P，Cao P J.Study on the Scheme of Testability Demonstration Test Based on Development Information［J］.Acta Aeronautica et Astronautica Sinica，2012，33（1）：2057-2064.

［2］明志茂，陶俊勇，陈循，等.动态分布参数的贝叶斯可靠性评估［M］.北京：国防工业出版社，2011.

［3］姜同敏.可靠性与寿命试验［M］.北京：国防工业出版社，2012：250-255.

［4］李晓阳，姜同敏，肖良华.成败型一次抽样检验方案算法的等价变形［J］.北京航空航天大学学报，2005，31（8）：904-907.

［5］何国伟，戴慈庄.可靠性试验技术［M］.北京：国防工业出版社，1997：88-97.

［6］GB/T5080.5-1985.设备可靠性试验方案成功率的验证方案［S］.北京：国防科工委，1985.

Optimization Algorithm of Type-ⅡCensoring of Considering both Sides Risk Inspection Plan of pass-fail Experiment

DU Xu1，WANG Zhuo-jian1，MA Tao2，SHEN An-wei1
（1.School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi'an 710038，China；2.China Flight Test Estabishment，Xi'an 710089，China）

When it comes to the problem of computational complexity and low flexibility，the paper designs a strong applicability and flexibility of the optimization algorithm，considering the success of both the risk of different Type-ⅡCensored sampling program design.With the analysis of accumulation equation and monotonous regularity，the optimization algorithm uses the method of dynamic step.Aiming at the difficulty of selection principles of different risks in using process，combined risk both in the initial agreement of equality and inequality，and choosing risk nearly as the basic principle，the criterion equation of risk selection is build.Finally，the calculating results of the traditional method and the optimization algorithm are analyzed，and the results show that not only high computational efficiency has been promoted，but also the engineering practicability enhanced.

type-Ⅱcensoring，algorithm，risks，pass-fail

V37

A

1002-0640（2015）08-0052-04

2014-06-11

2014-07-27

国家部委基金（513270303）；陕西省软科学技术基金资助项目（2011KRM122）

杜旭（1990-），男，河南内乡人，硕士研究生。研究方向：飞机RMS论证与评估。