水平层状介质射线追踪方法的Matlab实现

陈连木，万永革＊，陈 鑫

（1.防灾科技学院，河北 燕郊 065201；2.广西地震局，南宁 530022）

0 引言

地震学中的射线追踪法是指给定发射点和接收点位置及介质的波速，求从发射点到接收点的射线轨迹及其走时。作为一种快速有效的波场近似计算方法，地震射线追踪对研究波在介质中的传播路径和层析成像有重要的意义。传统的射线追踪方法通常包括边值问题的弯曲法和初值问题的试射法。试射法在全局搜索接收器方面效果较好，而弯曲法的计算效率较高。为解决两点间射线追踪问题，许多学者提出了解决方法。高尔根、徐果明［1］提出了逐步迭代射线追踪方法，但没考虑对超低速区的处理；徐昇等［2］提出了射线追踪的微变网格方法；张霖斌等［3］提出有限差分法射线追踪；Langan［4］等在Cassell［5］的基础上，设块内速度线性变化，并按Cassell的思路实现射线追踪。本文主要是以一维速度模型追踪水平层状介质2点的方法为原理，通过Matlab程序实现该种方法的计算结果，并与其他方法进行比较，指出其优势与不足。

1 射线追踪方法

1.1 “打靶法”

打靶法是已知射线的起始点位置和给定的初始方向，通过扰动初射方向来确定射线路径。已知地震位置和台站位置，算出震中距，利用试射法求得在震源层的θj，试射法的思路是：对于第1层的震源，不必用试射法，离源角通过可直接求出。对于位于其它层的地震，由于地下介质速度随深度会增大，台站所在的位置一定在离源角的αmin＝arctan（最小值）和（最大值）所射出的射线到达地面的位置之间（h为震源深度，dz为震源到该层底部的距离）。我们以这2个边界为初值，以它们的平均值为离源角，利用Δ ＝dz·。试算出射到地面的震中距（θj为震源层的入射角，νj为震源层的速度，νl为第1层的速度）。如果此震中距大于台站的震中距，则说明离源角取得大了，则令αmax＝α；反之，则说明离源角取得小了，则令αmin＝α，进行下一次迭代；再次以为离源角迭代计算。这样反复迭代直到计算得到的震中距和实际台站震中距在一定的误差范围内，则此时的离源角θj就可直接射到台站上［6］。

图1 打靶法— 直达波传播示意图

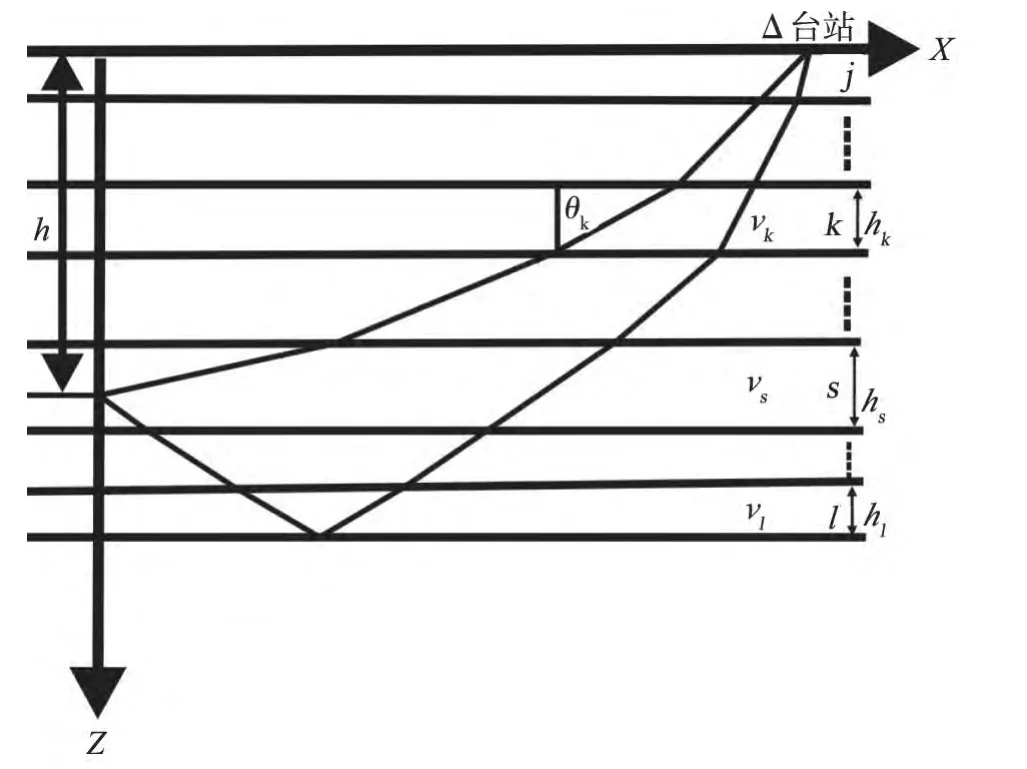
图2 求解p参数法路径示意图

1.2 求解p 参数法

求解p参数法是求解满足震中距的方程式（1）的射线参数p。由于p参数为离源角正弦和该层速度的比值，知道了该层速度就知道了射线在这里如何弯曲。震中距的表达式为

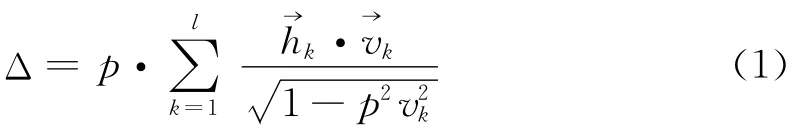
震中距Δ0的表达式可以写成关于p的非线性方程

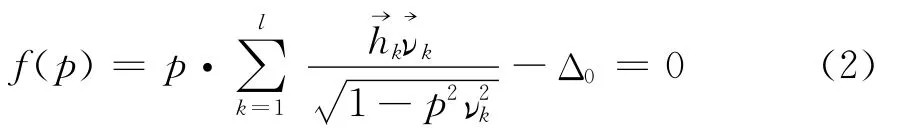
该方程可采用牛顿迭代法进行求解，该算法必须给定初始p参数作为第一次迭代的初始值，其一阶迭代公式为

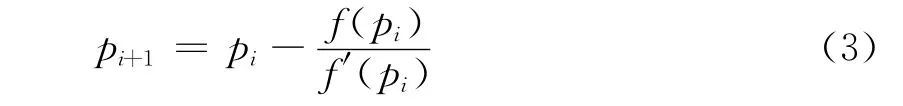
其中，f（pi）为（2）式的值，f′（pi）为（2）式的1阶导数，i为迭代次数。这样逐次迭代，直到得到的震中距和实际台站震中距在一定的误差范围内。

这种方法在震中距不大的情况下（Δ0＜24.6 km）都可以适用。但是当震中距较大时，由于最大速度层（速度为νm）中的入射角θm趋于π／2 时，θm＝，即p很小的变化就会引起θm的巨大变化，从而导致震中距Δ的巨大变化而出现发散。因此，只能求解较小震中距的地震波走时。

1.3 改进后的求解p 参数法

由于上面的迭代算法在震中距较大时发散，田玥［7］提出了改进后的成层介质中计算p参数的算法，其步骤如下：

改进后的方法是通过将射线参数p转换成别的参数q，q是最高速度层中射线走过的水平距离，νm是最高速度层中的速度。

p与q的转换关系为

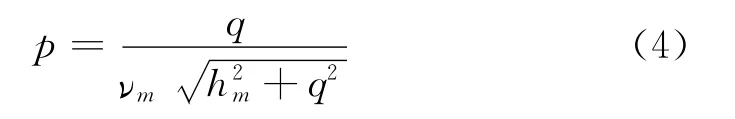
则q与震中距的关系为

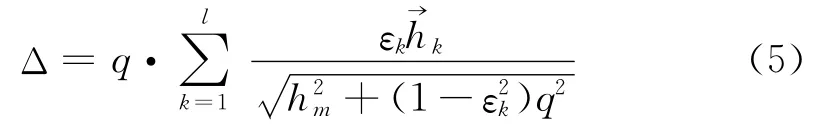
同理，方程（5）可以写成关于q的非线性方程

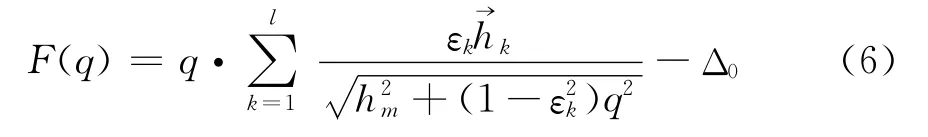
用牛顿法求解方程（6）的公式为

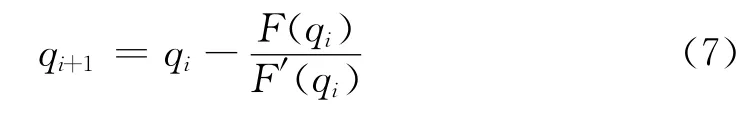
将得到的新参数q通过公式（4）转换为射线参数p。用牛顿法求解过程需要对q0的初值进行估计［7］。

2 两点间射线追踪的Matlab程序流程

编制程序的核心是水平层状介质2点间射线追踪。我们根据给出的震中距求得p参数。为了增加结果的准确性，分别运用正、逆梯度速度模型以及含有高速层的速度模型进行模拟。

程序流程见图3：

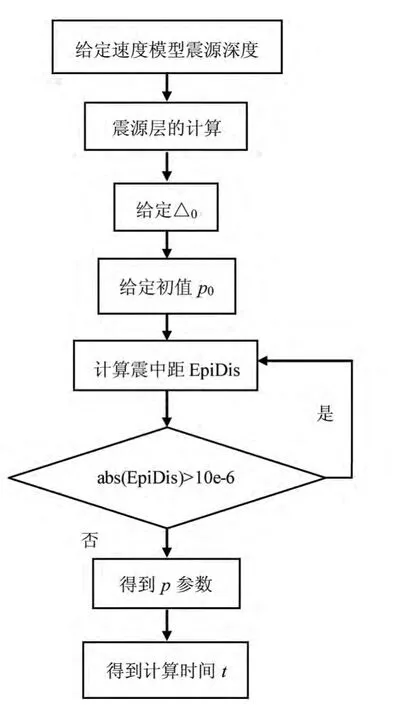
图3 平层介质射线追踪流程图

程序运行时应注意以下问题：

在进行逆梯度速度求解时应注意：对于打靶法最大离源角αmax的初始值应该设为，其中νj为震源层的速度，νm为最高速度层的速度。这是因为，当时，Δ将表现为虚数。

3 三种方法的比较

在计算精度和速度结构相同 的情况下，比较3种方法的所用时间。其中，直达波的震源深度设为19km，反射波的震源深度设为13km，计算精度均设为1.0×10－6。

首先，利用不同梯度速度结构和假定的震源深度运行射线追踪程序，变换不同的震中距得到一系列追踪的震中距—走时数据（图4）。可以看出，在计算精度一样，震中距一样的情况下，无论是对于含有高速层的正速度梯度还是逆速度梯度的直达波、反射波来说，都有以下特点：

表1 地壳速度模型

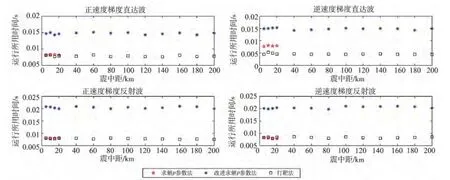
图4 3种方法在不同速度模型下的计算效率

①于求解p参数法而言，该种方法只能求解震中距较小（小于24.6km）的p参数，这是因为当震中距较大时，由于最大速度层（速度为νm）中的入射角θm趋于π／2时，，即p很小的变化就会引起θm的巨大变化，从而导致震中距Δ的巨大变化而出现发散。

②对于直达波、反射波来说，打靶法所用的时间总是最短（追踪速度为改进后的求解p参数法的2～3倍），求解p参数法次之，而改进后的求解p参数法所用的时间相对较长。这是因为改进后的求解p参数法在用牛顿迭代法求解q时需要进行较为复杂的求导运算，并且最后还需将参数q转换为参数p，故所用时间相对较长。

③3种方法的求解时间相差较小，而且求解时间也较快，最长时间也不超过0.025s。

4 结论与讨论

本文采用MATLAB 程序编制了打靶法、求解p参数法和改进求解p参数法实现了水平成层介质中的射线追踪算法，并对算法的运行效率进行比较。可得出，直接求解p参数法所能追踪到的距离较短，故该方法只适合小距离的追踪；改进后的求解p参数法能够追踪的距离较远，但是所用的时间相对较长；打靶法的追踪速度较快，并且追踪的距离也较远。

本文是在水平层状介质中进行的一维射线追踪，对只考虑三维速度结构的情况没有进行尝试，但目 前 地 震 定 位［8－11］、近 震 地 壳 模 型 的 计 算［12－16］大 多采用成层速度模型进行计算。因此，进行该模型的探讨对于理解地震走时计算和反演成层速度结构均有重要的理论意义。

［1］ 高尔根，徐果明.二维速度随机分布逐步［J］.地球物理学报，1996，39：302－308.

［2］ 徐昇，杨长春，刘洪，等.射线追踪的微变网络方法［J］.地球物理学报，1996，39（1）：97－102.

［3］ 张霖斌，刘迎曦，赵振峰.有限差分法射线追踪［J］.石油地球物理勘探，1993，28（6）：673－677，648.

［4］ Langan R T，Lerche I，Cutler R T.Tracing of rays though heterogeneous media：an accurate and efficient procedure［J］.Geophysics，1985，50（9）：1456－1465.

［5］ Cassell B R.A method for calculating synthetic seismograms in laterally varying media［J］.Geophysics，1982，69（2）：339－354.

［6］ 万永革.地震学导论［M］.北京：科学出版社，2015.（待出版）.

［7］ 田玥，陈晓非.水平层状介质中的快速两点间射线追踪方法［J］.地震学报，2005，27（02）：147－154.

［8］ 万永革，李鸿吉.遗传算法在确定震源位置中的应用［J］.地震地磁观测与研究.1995，16（6）：1－7.

［9］ 万永革，盛书中，程万正，等.考虑到时误差的地震定位算法及其在四川地区2001－2008年地震定位的应用［J］.地震地质，2012，34（1）：1－10.

［10］ 刘双庆，谢静，王熠熙.一种提高振动源扫描算法信噪比的方法［J］.华北地震科学，2015，33（1）：46－51.

［11］ 刘芳.用sPn震相计算内蒙古地震震源深度.大地测量与地球动力学.2010（30）增刊（II）：14－17.

［12］ Kissling E.Geotomography with local earthquake data［J］.Reviews of Geophysics，1988，26（4）：659－698.

［13］ Kissling E，Ellsworth W L，Eberhart－Phillips D，et al.Initial reference models in local earthquake tomography［J］.J Geophys Res，1994，99（B10）：19635－19646.

［14］ 贾丽华，李秀丽，李君，等.利用宽频带地震数据资料研究辽宁地区的地壳结构［J］.华北地震科学，2013，31（3）：1－7.

［15］ 孙译，赖晓玲.利用断层围陷波资料研究汶川MS8.0地震构造特征［J］.华北地震科学，2014，32（3）：1－4.

［16］ 陈立军，胡奉湘，陈晓逢.全球地震柱的地震层析成像证据［J］.华南地震，2013，33（4）：1－10.