随机振动有限断层方法计算衡水市强地面运动参数
刘博研,申文豪,史保平
(1.中国地震局地壳应力研究所(地壳动力学重点实验室),北京 100085;2.中国科学院大学,北京 100049)
0 引言
研究强地面运动对于减少震害,保护人民生命财产安全具有重要意义。强地面运动研究的科学目的是揭示地震引起地震动的机理,为强地震动的预测提供理论基础。20世纪90年代末至今的二十几年间,强地面运动观测记录累积得很快,包括1989年 美 国Loma PrietaMW7.0 地 震、1994年 美 国NorthridgeMW6.7 地震、1999年中国台湾MW7.6地震以及2008年汶川MW7.9地震、2010年墨西哥BajaMW7.2地震等,每一次地震都积累了几十乃至上百条强震记录,这些记录对于获得强地面运动规律具有重要的科研价值。尽管这些强震记录对强震观测数据库做了极大的补充,但是目前仍然没有从根本上解决强地面运动观测缺乏的问题。
由于中强地震观测数据缺乏,发展强地面运动的模拟技术已成为定量化估计强地面运动的重要手段。地震学家在建立模型的探索中发现,模型建立过程必须把震源破裂过程、地震波传播过程以及场地效应作为一个系统来考虑。准确地预测强地面运动,不仅对了解地震的震源物理和力学过程有重要的理论价值,而且在工程抗震和地震灾害的定量化评估、灾后救援、政府决策中有着重要的实际应用价值。强地面运动预测还是地震风险评估和未来潜在地震危险性区划工作的重要组成部分。利用区域历史地震活动性资料、地质(断层)资料、活动断层探测成果、GPS(大地测量)数据以及其他地球物理资料,结合计算机网络化GIS可视化技术,实施基于物理的地震动数值模拟技术,可为未来中强地震潜在危险性分析提供合理参数,为区域地震风险估算提供新的技术支撑平台,弥补传统方法的局限性。未来潜在中强地震活动区内地面运动的模拟计算成果可为区域内地震危险性分析提供合理的约束。
事实上,地震波的产生与传播是极其复杂的过程,真实的地震波并没有固定的振动周期,其振幅也是随时间变化的[1]。在地震工程学中,常常把任意一条真实的地震波看成有限持时的随机振动波,对于任何实测的地震波每一个频率均有相应的傅里叶谱值[2]。很多学者在模拟地震波的过程中考虑了这种随机性[3-4],在地震工程中利用随机理论模拟强震地面运动有了很大的发展。随机方法的基本原理是把远场地震动看成是有限带宽、有限持时的高斯白噪声,并把影响地震动参数的一系列因素(包括震源、路径和场地)在频率域里表达成简单的乘积形式,然后与通过窗函数调整的噪声傅里叶谱结合,最后通过傅里叶反变换得到地震动参数的时程曲线。随机方法的震源理论模型是Brune[5]在1970年首次提出的垂直断层面辐射剪切波的震源模型;Hanks和McGuire[6]等人在1981年提出了随机振动理论计算峰值加速度和峰值速度的公式,为随机性模拟地震动峰值做出了理论上的贡献;1983年,Boore[4]在Hanks 和McGuire[6]等 人 的 工 作 基 础上,开创性的将蒙特卡罗方法应用其中,给出了随机点源模型,实现了地震动时程及反应谱的估计;1984年,Atkinson[7]在Hanks和McGuire[6]与Boore[4]等人的研究基础上给出了三段几何衰减模型,进一步修正了随机振动方法在远场的应用。至此,随机性方法的框架已经基本构建完善。若以震源类型进行分类,可将计算模型简单分为点源模型和有限断层模型,前者将震源简化为一个点源,这类模型多用于对强地面运动的简单估算及远场强地面运动的模拟。而在近断层范围内,地面运动直接同断层破裂过程相关,断层的走向、倾角、滑移方向等都会对地表运动的形态产生影响。因此,采用点源模型模拟强地面运动的时空变化特征显然无法满足工程抗震设计和地震灾害预测的需要。对于中强地震采用有限断层模型更为合理。
针对强地面运动的研究涉及多种震源理论和断层模型,在本研究中,我们着重介绍用随机振动的有限断层模型来计算衡水市强地面运动参数以及设定地震的时程曲线。
1 方法原理
1.1 随机振动有限断层
Beresnev和Atkinson[8]等对随机点源方法做了改进,提出随机有限断层方法。其基本思路是将断层面分成N个大小相等的矩形子断层,每个子断层即为1个点源。通过设定震源模式和破裂传播速度,就可以得到子源破裂的时间顺序,然后根据子源与场地的几何关系,计算每个子源对场地的影响,即可叠加成场地的地震动时程。该方法在我国得到了广泛的应用,李启成[9]比较了随机点源和随机有限断层2种方法,指出2种方法的适用性和局限性,并模拟了1982年ML5.1地震和1976年MS6.9宁河地震。王国新和史家平[10]、王海云[11]利用随机有限断层模型分别进行了汶川地震和1994年Northridge地震的强地震动模拟,模拟结果与台站记录一致性较好。陶夏新和王国新[12]论证了这种随机方法在合成的时程中破裂的方向性效应和上盘效应的有效性。在国外,随机振动的有限断层模型也已被广泛应用于已发地震的强地面运动模拟,以及对未来地震或者设定地震强地面运动的预测。Atkinson和Boore[13]用改进后的随机有限断层模型模拟了美国东部地区的强地面运动,结合模拟数据和台站记录发展了美国东部的衰减关系。Chopra等[14]基于随机振动的有限断层模型模拟了2001年MW7.6印度Bhuj大地震强地面运动参数,并利用模拟得到PGA 计算出了理论MMI的分布图。Zafarani等[15]用该模型评估了伊朗8个重要地震,并预测了大德黑兰地区未来地震的强地面运动参数。
在随机有限断层模型中,断层破裂面被分成N个大小相等的矩形子源,每个子源即为1个点源,每个子源满足ω2衰减规律。通过设定震源模式和破裂传播速度,可以得到子源破裂的时间顺序,然后根据子源与场地的几何关系,计算每个子源对场地的影响。所有子源在观测点引起的地震动在时域中以适当的延迟时间叠加,即可获得场地的地震动时程a(t):
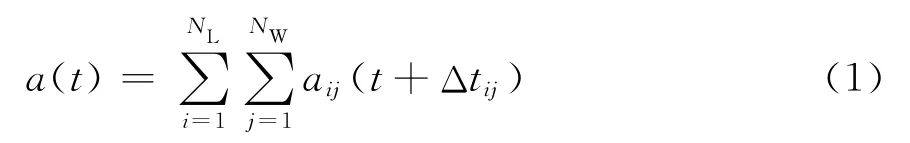
式中:NL、NW分别为断层沿长度和宽度划分的子断层数;i和j分别代表沿断层走向和倾向方向的断层指标(Index);Δtij为子源(下标为ij)到场地的滞后时间;aij(t)为子源(下标为ij)利用随机点源方法得到的在观测点的加速度。
在有限断层中,为了保证断层辐射的总辐射能量守恒,子断层上划分有严格的要求,Atkinson和Silva[16]指出用随机模型合成地震动时,子断层大小为:
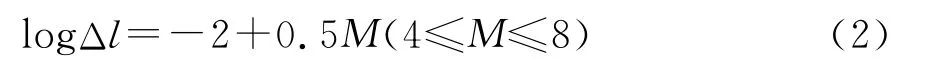
式中:Δl为子断层尺度,单位为km;M为地震震级。断层总面积除以子断层的面积就是断层上子断层的个数。由于子断层的大小有严格的规定,单次触发的子断层地震距的总和往往小于总地震距。为了保证总地震距守恒,常常采用部分子断层多次触发的方式。针对有限断层模型的这些不合理之处,Motazedian和Atkinson[17]提出了“动力学拐角频率”的概念。他们认为,在断层面破裂过程中拐角频率是一个时间的函数,与破裂面积成反比,破裂从高拐角频率开始,随着破裂面积的扩大,拐角频率逐渐降低,子断层之间相互独立。动力学拐角频率为:
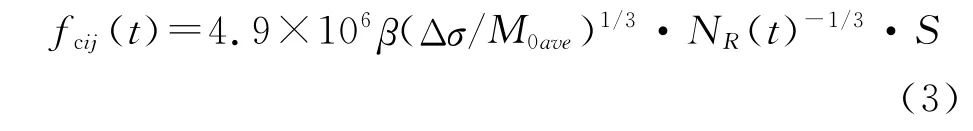
式中:fcij(t)为第ij个子断层的动力学拐角频率;t是第ij个子源被触发的时刻;NR(t)是在时刻t已破裂子断层的累计数;M0ave=M0/N,是子断层的平均地震矩;S是表示子断层辐射强度的一个常数。随着破裂的传播,破裂的子断层数增加,子断层拐角频率减小。为了使断层总辐射能守恒,引入一个标度因子H,动力学拐角频率对子断层总辐射能的递减影响到标度因子H的补偿,总辐射能保持不变。这样,在保证辐射能守恒的前提下避免了子断层多次触发这一非物理现象。至此,随机振动的有限断层方法的理论框架基本得到完善。
1.2 浅层横波速度V30对地震动模拟结果的影响
在宏观地震震害调查中发现,一般软弱地基上的震害较坚硬地基上的震害重。随着进一步研究,人们认识到浅层速度结构对场地强地面运动有很大影响,表现为对地震动的放大或缩小,常被看作引起场地效应的重要原因,直接影响到地震灾害的严重程度。因此,在数值计算中浅层速度结构对强地面运动的影响必须考虑。
在随机有限断层模型中,若要得到浅层横波速度对某场点地震动的影响,必须将该点浅层各个深度的速度结构加入到程序中运算。对于大规模、高精度的网格运算而言,由于构成场地的岩土及其所含各种结构面是在漫长的地质历史中形成的,并经历了复杂的地壳构造运动的改造,所以在一般情况下场地条件都比较复杂,显然不可能获得每个场点不同深度的浅层速度结构。Wald和Allen[17]根据全球地形数据给出了全球范围内浅层速度结构数据V30,V30不是严格意义的地表30 m 以下的横波速度,而是全球平均意义下的浅层横波速度,能够反映地表浅层横波速度在横向上的变化,因此,可以用来进行强地面运动的模拟。V30数据范围为180~760 m/s,通常认为760 m/s为一般情况下基岩的速度结构。接下来的问题就是如何处理V30对地震动参数的影响。Boore和Atkinson[19]在建立衰减关系NGA(Next Generation Attenuation)时将地震动参数Y 的构成写作(4)式:
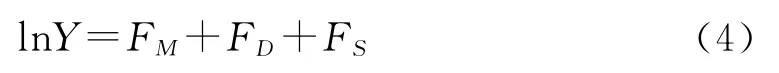
式中:FM、FD和FS分别代表震级影响、距离影响和场地放大效应。FS是由线性部分FLIN和非线性部分FNL两部分组成,并且线性部分占绝大部分,非线性部分可以忽略不计。如果地震动参数Y为PGA,那么FLIN=-0.36ln(V30/760);如果Y是PGV,则FLIN=-0.6ln(V30/760)。如果将基岩上的强地面运动参数设为Y,那么增加了场地放大效应后的强地面运动参数可设为Y′,可得:

因此,如果我们能够获取计算区域内网格点上的V30分布,那么增加场地影响后的地震动参数为:
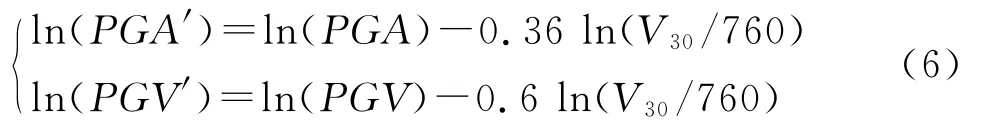
这样,我们就能将V30的影响加入到强地面运动模拟的结果中,使得模拟结果能够充分反映浅层速度结构的影响。
2 强地面运动模拟及时程曲线的计算
衡水市位于河北省东南部,是重要的区域经济文化重镇。衡水地区在大地构造上属中朝准地台的二级构造单元——华北断坳区,它是我国最古老的陆块之一,经历了太古代和早元古代基底形成、晚元古代至三叠纪盖层发育和中、新生代以来地壳活化3个构造演化阶段。在地壳活化阶段,华北断坳发生大规模的伸展裂陷作用。早第三纪发育了众多的NE 向或NNE 向断陷盆地,形成典型的盆岭构造;晚第三纪华北断坳大面积沉降,上第三系超覆于整个盆地;第四纪进一步发展,但构造分异比较显著,形成了一系列隆(坳)、凸(凹)相间结构。平原地整体由东向西缓慢掀斜,内部地势平坦,一般海拔高100m 以下,大部分小于50m。衡水市位于华北平原拗陷区中的邢衡隆起、冀中坳陷和沧县隆起交汇地带,第四系厚度为350~400m。
根据衡水市城市发展和防震减灾的需要,以及主要断层的实际情况,确定本研究的目标区东西长30km,南北宽25km,面积约750km2。地理坐标为:北纬37.66°~37.81°,东经115.52°~115.78°。为了考虑衡水市周边断层的影响,将工作区域扩大为北纬37.0°~38.5°,东经114.5°~116.5°区域内,包含(1)沧西断裂,(2)旧城北断裂,(3)护驾池断裂,(4)新河断裂,(5)前磨头断裂,(6)明化镇断裂,(7)衡水断裂,(8)德州断裂(图1)。鉴于旧城北断裂(2)和德州断裂(8)只有极小一部分分布在近场区内,我们只对其他6条断层进行设定震级条件下的强地面运动评估。
考虑断层活动性,我们将依据断层长度得到各条断层的最大震级与第5代潜在震源区划图进行对比。综合评定后,得到活动断裂潜在最大震级(表1)和随机有限断层模型输入参数(表2)。
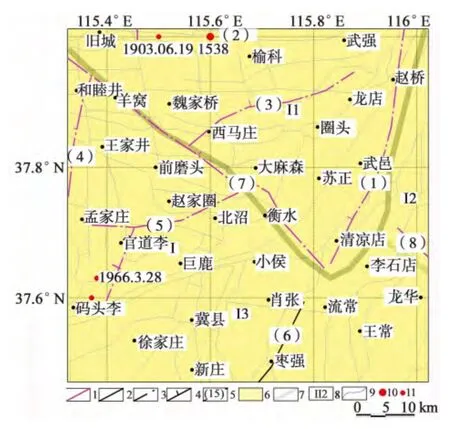
图1 地震构造图
3 结果分析与讨论
本研究将研究区域划定在(37.4°~38.0°N,115.2°~160.0°E),区域网格大小为0.6°×0.8°,网格精度为0.005°(0.5km),利用随机振动有限断层模型计算每个网格点的峰值加速度(PGA)、峰值速度(PGV)以及网格点到断层的最短距离D。我们拟采用的计算流程是:
第1步:选定研究区域。根据地震地质和地震活动性调查以及地球物理资料确定发震断裂的位置、产状、埋藏深度等性质。根据震级大小以及震后可能造成的影响,选取合适的计算范围。
第2步:利用随机振动的有限断层模型计算研究区域PGA、PGV 以及网格点到断层的最短距离。根据第1步划定的研究区域大小,我们会根据断层的长度、宽度划分合适的子断层数目以及网格点的精度(为确保计算结果精确,设定计算网格点间距为0.005°),根据构造地质结果以及历史地震等资料确定发震断层的应力降和几何衰减因子等参数。
第3步:加入浅层速度结构的影响。在第2步计算得到初始地震动参数后,充分考虑浅层速度结构对地震动的影响。

表1 结合断裂活动性估计潜在最大震级
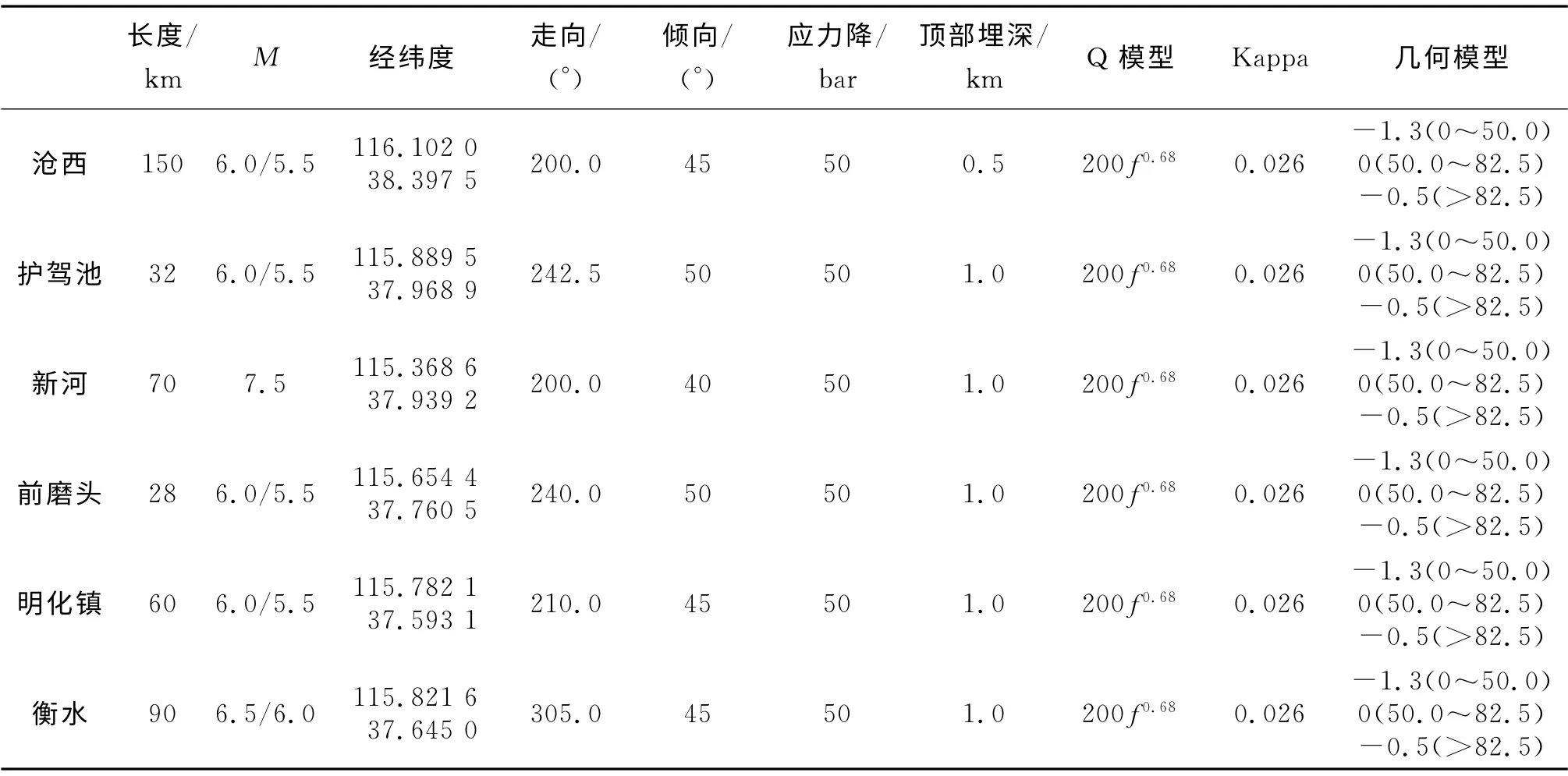
表2 各设定发震断层使用的随机有限断层模型输入参数1 出自河北省活断层探测与地震危险性评价项目衡水市目标区断层危害性评价报告
计算出区域峰值加速度以及峰值速度分布后,我们计算不同等级的加速度、速度以及位移的时程曲线。通过输入模型参数,按照上述步骤得到6个衡水设定地震的峰值加速度以及衡水市区的时程曲线(图2~图7)。
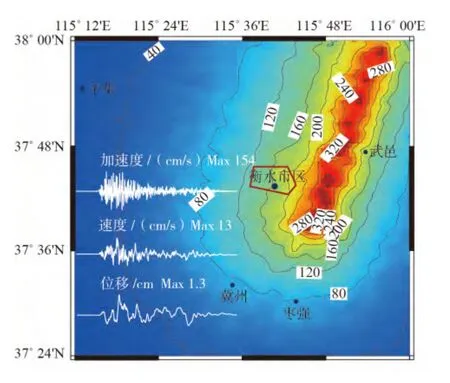
图2 沧西断裂设定6.0级发震断层产生的峰值加速度及衡水市区时程曲线图
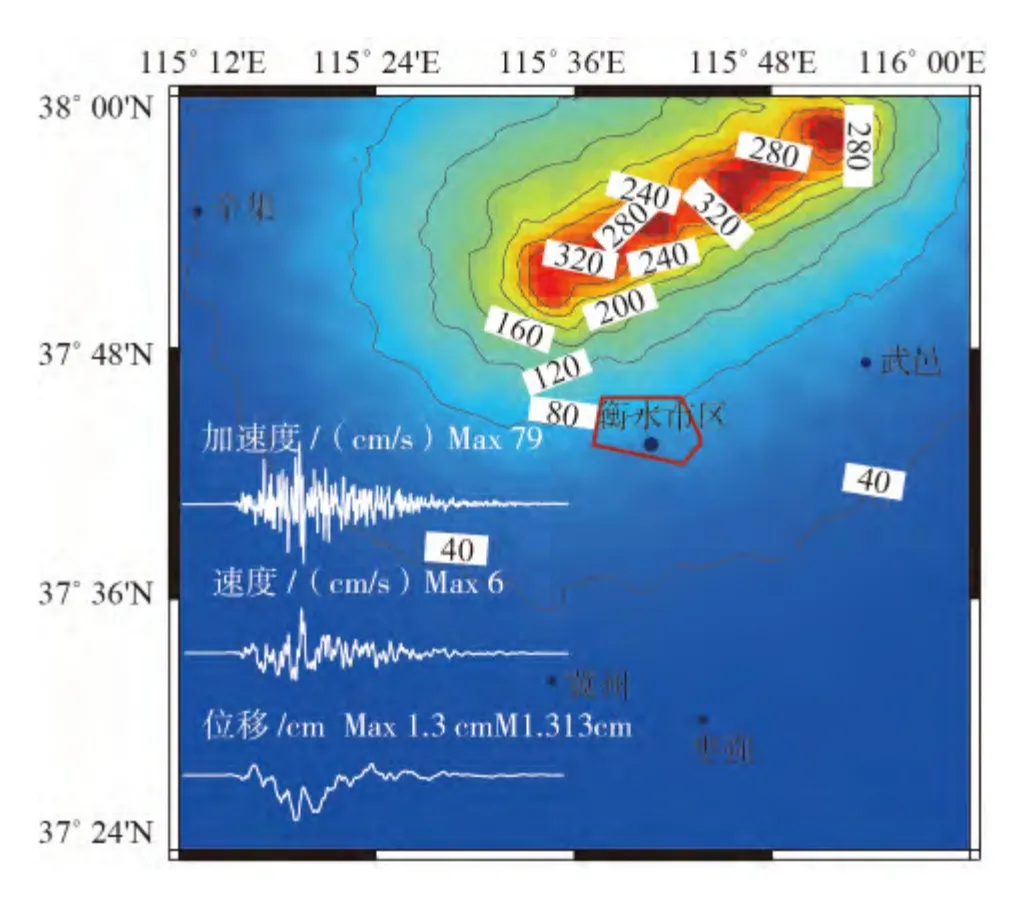
图3 护驾池断裂设定6.0级发震断层产生的峰值加速度及衡水市区时程曲线图
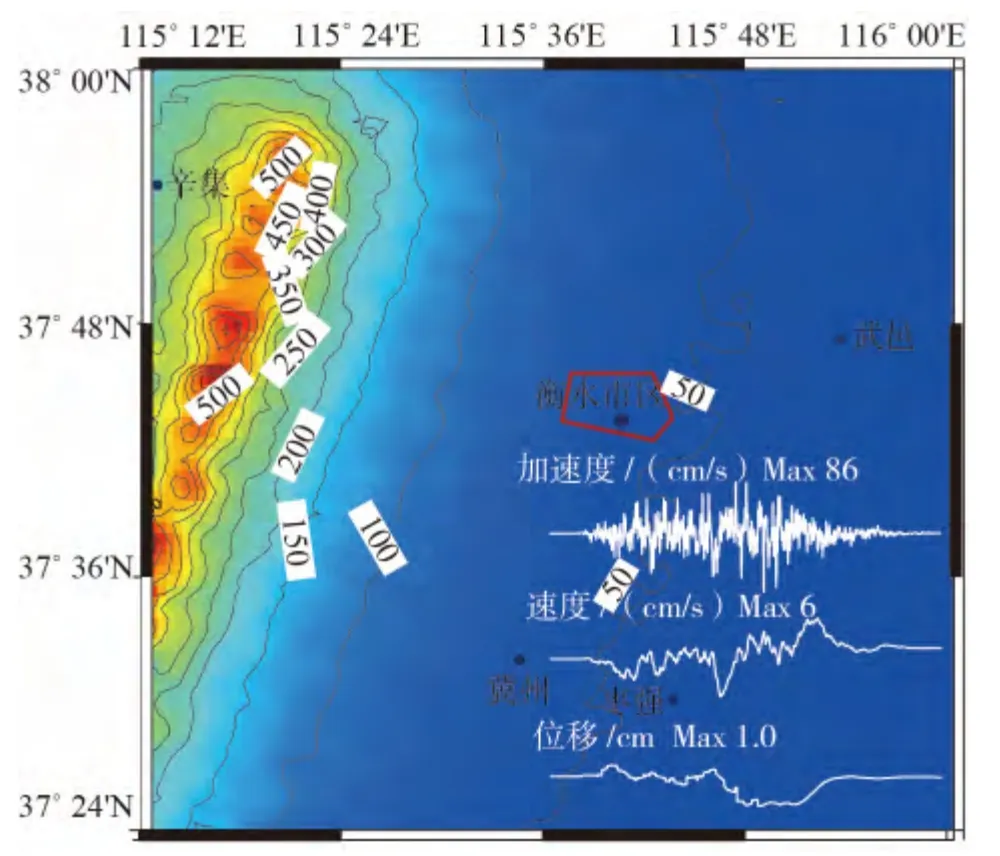
图4 新河断裂设定7.5级发震断层产生的峰值加速度及衡水市区时程曲线图
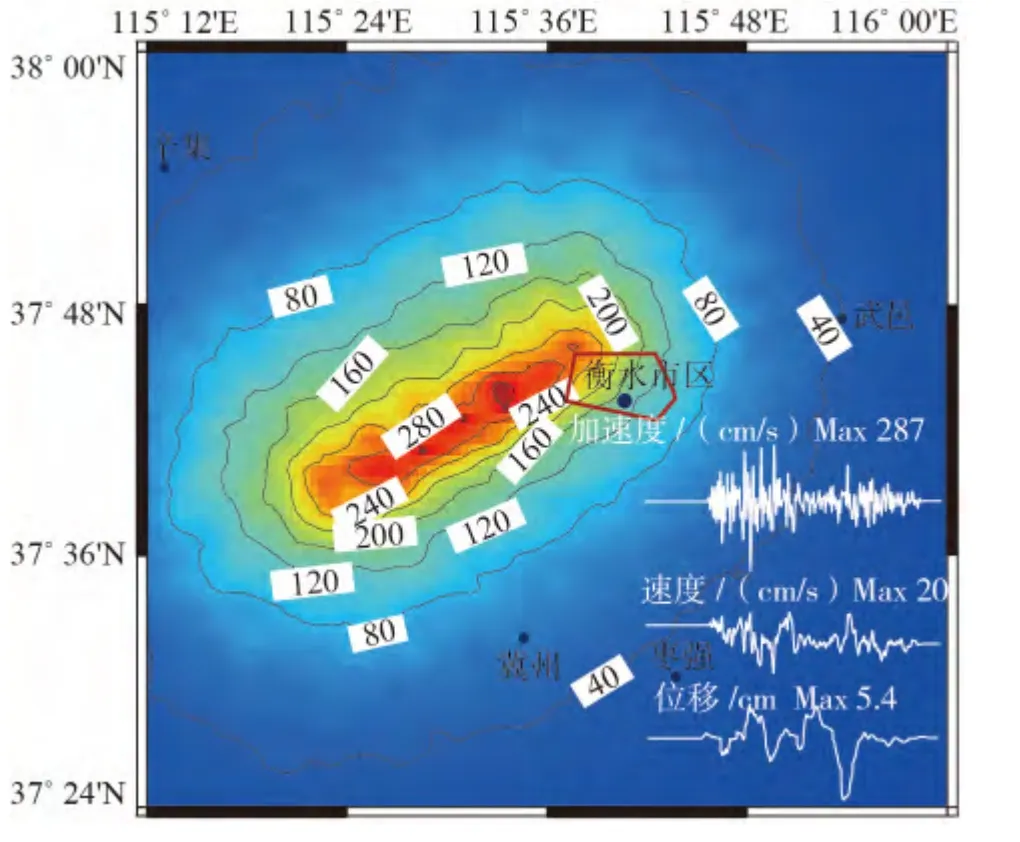
图5 前磨头断裂设定6.0级发震断层产生的峰值加速度及衡水市区时程曲线图
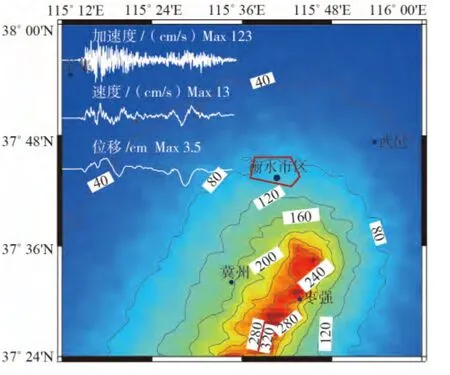
图6 明化镇断裂设定6.0级发震断层产生的峰值加速度及衡水市区时程曲线图
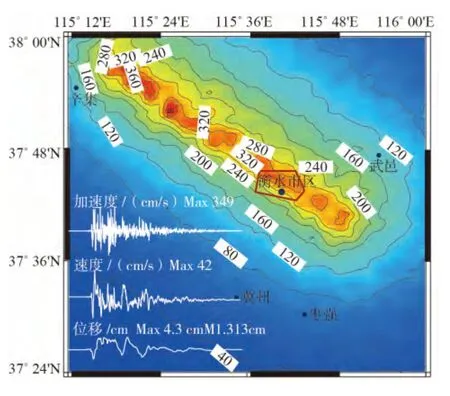
图7 衡水断裂设定6.5级发震断层产生的峰值加速度及衡水市区时程曲线图
由于本研究设定的断层埋深都比较浅,地震辐射能量集中于地表浅层。衡水市区与几条断层的距离都比较近,因此地震辐射能量衰减较少,在衡水市的强地震动效应也很明显。由6条设定断层强地震动计算结果看出,对衡水市区危害相对最小的是新河断裂和护驾池断裂,峰值加速度值在50~90cm/s2左右,峰值速度在10cm/s以下,这一值对应到GB/T 17742-2008《中国地震烈度表》为Ⅵ~Ⅶ度;对衡水主城区危害最大的是衡水断裂,峰值加速度值在200~360cm/s2左右,峰值速度在30~45cm/s之间,这一值对应的烈度值为Ⅷ~Ⅸ度。
本研究采用的强地震动预测方法(以下简称活断层方法)的原则是基于已经查明的断层,确定其可能发生的最大震级的地震前提下,对该断层相应的设定震级,通过确定性的方法(确定性模型)进行地震动预测,并考虑其一旦发生破裂时产生的地震动空间分布,是在设定断层的设定震级发生概率100%前提下得到的模拟数值,是针对性、确定性的结果。这种确定性的方法考虑了地震的震源特征、传播途径特性以及场地的放大效应,包含了强地震动模拟应当考虑的各种关联特性。
模拟得到设定震级地震强地面运动的结果对于未来划定该地区地震危险区具有很好的参考意义。由于该地区缺乏足够的强地面运动记录,无法利用实际记录到的地震动资料直接得到地震动衰减关系,而模拟得到的强震数据可以补充衡水地区强震数据的不足,利用这些强震数据可以建立衡水地区的衰减关系曲线,这对于未来地震动预测、工程场地地震安全性评价和地震区划工作将具有重要意义。由于随机振动有限断层模型没有考虑地震波在介质中的传播过程,不会像复合震源模型那样耗费大量时间在计算格林函数上,具备时效性强的特点,而这一点正是地震烈度速报所要求的。因此,未来该模型可以应用于地震烈度速报技术上,这对于震后应急响应将具有重要意义。综合以上结果,本研究系统化应用有限断层随机振动模型,对包括衡水地区在内的华北地区进行了地震风险评估及潜在震源的地震危险性分析,得到的基岩峰值加速度、峰值速度分布图可为进一步划定衡水地区地震危险区以及强地面运动特征分析提供参考依据。
致谢:感谢中国地震局地壳应力研究所马保起研究员和吴荣辉研究员对本工作的大力支持和热心指导。
[1] 陈运泰,顾浩鼎.震源理论基础[M].北京:中国地震局地球物理研究所,2007:111-115.
[2] 周锡元,吴育才.工程抗震的新发展[M].北京:清华大学出版社,2006:18.
[3] Boore D M.Simulation of ground motion using the stochastic method[J].Pure and applied Geophysics,2003,160:635-676.
[4] Boore D M.Stochastic simulation of high frequency ground motion based on seismological models of the radiated spectra[J].Bull seism Soc Am,1983,73(6A):1865-1894.
[5] Brune J N.Tectonic stress and the spectra of seismic shear waves from earthquakes[J].J Geophys Res,1970,75(26):4997-5009.
[6] Hanks T C,McGuire R K.The character of high frequency strong ground motion[J].Bull Seism Soc Am,1981,71:2071-2095.
[7] Atkinson G M.Attenuation of strong ground motion in Canada from a random vibration approach[J].Bull Seism Soc Am,1984,74:2629-2653.
[8] Beresnev I A,Atkinson G M.Stochastic finite-fault Modeling of ground motions from the 1994Northridge California Earthquake Validation on rock sites[J].Bull Seism Soc Am,1997,88(6):1394-1401.
[9] 李启成.经验格林函数方法模拟地震动研究[D].哈尔滨:中国地震局工程力学研究所,2010.
[10] 王国新,史家平.随机有限断层法在汶川强地震动模拟中的应用[J].自然科学进展,2009,19(6):664-669.
[11] 王海云.近场强地震动预测的有限断层震源模型[D].哈尔滨:中国地震局工程力学研究所,2004.
[12] 陶夏新,王国新.近场强地震动模拟中对破裂的方向性效应和上盘效应的表达[J].地震学报,2003,25(2):191-198.
[13] Atkinson G M,Boore D M.Ground-motion relations for eastern North America[J].Bull Seism Soc Am,1995,85(1):17-30.
[14] Chopra S,Kumar D,Rastogi B K.Estimation of Strong Ground Motions for 2001Bhuj(MW7.6),India Earthquake[J].Pure Appl Geophys,2010,167:1317-1330.
[15] Zafarani H,Noorzad A,Ansari A,et al.Stochastic modeling of Iranian earthquakes and estimation of ground motion for future earthquakes in Greater Tehran[J].Soil Dynamics and Earthquake Engineering,2009:29:722-741.
[16] Atkinson G M ,Silva W.Stochastic Modeling of California Ground Motions[J].Bull Seism Soc Am,2000,90:255-274.
[17] Motazedian D,Atkinson G M.Dynamic corner frequency:a new concept in stochastic finite fault modeling[C/OL].Victoria,British Bolumbia:Seismological Society of America Meeting.[2008-12-25].http://http-server.carleton.ca/~dariush/research/SSA2002.pdf
[18] Wald D J,Allen T I.Topographic slope as a proxy for seismic site conditions and amplification[J].Bull Seism Soc Am,2007,97(5):1379-1395.
[19] Boore D M,Atkinson G M.Boore-Atkinson NGA ground motion relations for the geometric mean horizontal component of peak and spectral ground motion parameters[R].PEER Report,Pacific earthquake engineering research center,2007.

