基于FOCMEC方法反演震源机制解的交互式程序研制与使用

刘泽民，倪红玉，张 炳，夏仕安

（安徽省地震局，安徽 合肥 230031）

0 引言

地震是地球内部岩石错动或者破裂释放能量的产物。地震激发地震波，地震波携带震源运动的信息，根据地震波的特性研究震源机制解就是为了弄清楚震源的运动过程［1］。震源的运动过程可以称为广义的震源机制解，而基于点源双力偶模型的震源机制则可以认为是狭义上的震源机制，它能描述震源的受力和错动方式。本文利用FOCMEC 方法反演的是狭义上的震源机制解。当前，震源机制解是地震学中的一个重要的研究方向，是开展震源物理、孕震过程等方面研究的基础资料，如震源机制解是研究区域构造应力场最基础的资料［2］，同时也可以用来计算强震前震源一致性参数变化［3－4］等等。因此准确、快速反演地震震源机制解是地震学研究中一项重要的基础工作。

利用震源激发的地震波反演区域地震的震源机制解有多种方法，如利用直达P波初动符号计算震源机制解是一种传统且简单易行的方法。但前提是所计算的地震被很多台站记录到［5］，且为了约束节平面的空间位置，最好要有紧靠节面位置的初动观测数据。而愈靠近节面，P 波越弱，初动越不易辨认［6］。因此这种方法很难确定震级较小、台站密度较低的地震震源机制解。在实际应用的过程中，某些极性记录不好的中等地震，甚至中强地震也很难准确反演其震源机制解，因此该方法在日常使用中具有一定的局限性。由地震激发的S波在节面附近的振幅最大，Kisslinger等［7］、梁尚 鸿等［8］利用垂直向SV 波与P 波的振幅比，结合台站的初动测定震源机制的方法，在模拟地震观测时期应用较为广泛。与SV 波相比，SH 波在自由表面入射时，不会产生反射P波，因此初动和振幅更加可靠。吴大铭等［6］推动了用SH 波和P波的振幅比求解震源机制方法的发展。近年来Snoke等［9－10］提出了利用P 波、SV 波、SH 波的初动和振幅比联合求解震源机制的方法，并通过IASPEI百年纪念向全球推广了一套计算程序（FOCMEC程序）。刘杰等［11］以2次中小地震为例，通过与P 波初动得到的结果进行对比，表明该方法能准确确定震源机制解。倪红玉等［12］以2005年九江－瑞昌MS5.7级地震为例，全面地讨论了该方法的影响因素。认为该方法是一种稳定、可靠的计算震源机制解的方法。

FOCMEC 方法，由于其约束参数大大增加，反演结果精度较高，并在国内外得到较为广泛的应用。该方法推广的FOCMEC 程序操作步骤复杂，虽然刘 杰 等［11］将FOCMEC 程 序 从Unix 系 统 移 植 到Windows系统，但仍然存在波形数据旋转读取困难、操作复杂且容易出错等不足。笔者根据日常工作的需要，利用Delphi面向对象语言，开发交互式地震波形读取程序，转换并集成FOCMEC 程序代码，形成交互式FOCMEC 方法的震源机制解反演程序。该程序最大限度地简化操作步骤、降低操作难度，能够完全兼容我国各个地震台网产出的EVT格式波形数据，便于推广应用。

1 原理与方法

在r－θ－Ф坐标系中，双力偶震源辐射的远场地震波位移在观测点P（r，θ，Ф）处的分量为［13］：

式（1）中：ρ是岩石密度，VP和VS分别是P 波和S波传播速度；r表示发生位移的点到震源的距离；t是时间，t＝0时是力矩作用的时间（即断层开始错动的时间）；˙M是双力偶中一个力偶强度随时间的微商。ur是P 波的位移表达式，uθ和uφ分别是SV 和SH 波的位移表达式。FOCMEC 计算程序所用参量为3个初动（P、SV、SH）和3个振幅比（SV／P、SH／P、SV／SH），这样每个台站记录所用的独立量就从传统的1个P波初动增加到5个（振幅比仅有2个独立分量）。通过比较理论计算和实际观测所得的P 波、SV 波、SH 波的初动符号和振幅比矛盾数最小的方式得到震源机制解，大大提高了反演结果的精度。

FOCMEC程序通过对比理论与实际观测P波、SV 波及SH 波的初动和振幅比，反演震源机制解。因此，首先需要根据台站和震中位置及震源深度，计算得到台站的方位角、离源角和入射角。方位角和离源角可以用来确定台站在伍尔夫坐标上的位置，而入射角则用于振幅比的自由表面校正。台站的方位角根据地理坐标求得，而离源角和入射角则根据给定的速度结构模型，基于Snell定理，利用打靶法计算得到。同时为了能顺利读取SV 和SH 波的极性和振幅，必须根据地震震中和台站的方位角，对水平记录的2个分量进行旋转，得到径向和切向分量。即

式（2）中：R（t）和T（t）分别表示径向和切向分量，N（t）和E（t）表示NS和EW分量记录，Az表示方位角。在该程序中P波、SV 波和SH 波的极性根据FOCMEC程序的约定保存。

2 波形读取与交互式震相分析

我国“九五”、“十五”地震台网产出的地震波形数据主要采用EVT 格式保存。目前，该格式仍然是地震波数据保存的一种主要方式，且“十一五”及以后的观测系统也可将地震事件保存为EVT 格式，因此交互式FOCMEC 方法反演震源机制解程序默认读取EVT 格式的地震波形数据，这样也便于计算早期地震的震源机制解。本程序采用面向对象的方式读取EVT 格式的波形数据［14］，同时根据我国“九五”、“十五”地震计不同的采样频率、精度，采用面向对象中多态的编程手法，准确读取地震波形。运行程序后，首先调入地震事件的EVT 数据波形文件，根据上述原理，还应输入地震的经纬度和深度信息（图1）。程序根据地震震中和台站的经纬度自动将地震波形进行旋转，得到径向和切向的地震波形，加上原来的三分向地震波形，主界面会显示5个分向的波形。对于早期的单分向（垂直向）地震记录，本程序同样也支持其产出的波形数据，并可交互式读取垂直向的极性和振幅。该程序根据球面三角公式，在后台自动计算得到台站的方位角和震中距。此外程序根据地震的震中经纬度、深度和台站的经纬度，以及给定的速度结构模型，基于Snell定律和打靶法，可以计算得到P 波或者Pn波的离源角和入射角。经过大量严格的对比测试，其计算结果与Snoke［9］和刘杰等［11］提供程序的计算结果高度吻合。台站的方位角、离源角、震中距以及地震波的相关信息（如地震波的时间信息）和地震的经纬度信息在程序主窗口最下面的状态栏显示。可以根据这些信息辅助交互读取地震波的震相，如可以根据震中距的信息确定台站是否能记录到首波等。

图1 读取地震波形

一般来说，震中距越近的台站记录越清晰可靠。为了更为方便地交互读取地震波形的震相，程序自动根据各个台站的震中距进行排序，并将排序后的台站名称列表放置在台站名下拉框中。在实际的应用过程中，只需要根据下拉框中的台站顺序，即震中距顺序，依次交互读取台站的震相（图2）。

图2 显示台站波形信息

FOCMEC法采用直达P（含Pn）、SV 和SH 波的极性以及P／SV、P／SH 的振幅比反演震源机制解。因此，在交互式读取地震波形的时候，需准确判断各个台站的各种震相的极性以及相应的振幅。首先可以通过鼠标拉框对地震波形进行水平向缩放：在地震波形上从左到右拉框，即可实现对选定波形水平放大到整个波形显示区域；而从右向左拉框，则水平缩小到最原始状态。同时，在主界面上方工具栏的垂直缩放按钮，可以对地震波形进行垂直向缩放。将地震波形水平和垂直缩放到合适位置，使其能准确辨认各种震相的极性和振幅。图3为在垂直向通过右击鼠标，弹出菜单来读取直达P 波的极性，对于Pn波也可采用类似的方法。在交互读取直达P波的极性后，程序会在垂直向的地震波形的右击鼠标位置显示该极性，同时程序会在后台记录该信息，在地震波形缩放后仍能在正确位置正常显示，以下所有的交互读取的极性和振幅均有类似的功能。本程序中直达P（含Pn）波的极性必须在垂直向读取，在水平向右击鼠标弹出的菜单，P波极性选项菜单为禁用状态，最大限度减少不必要的误操作。图4为在切向读取SH 波的极性。S波的极性对反演震源机制解的节面位置有很好的约束作用，因此，应尽量读取清晰的SH 波极性。在实际应用过程中，S波的极性不易辨认，尽量不要读取不清晰的S波极性。其操作方式与读取P 波极性较为类似，首先将地震波形缩放到合适的大小，然后在切向波形的合适位置上右击鼠标，通过辨别波形和弹出的菜单，读取SH 波的极性。当震中距很小时，如小于震源深度，SV 波的极性应优先在垂直向读取；而当震中距远大于震源深度时，则应在径向读取，其读取方法与SH 波完全相同。

图3 读取垂直向直达P波极性

图4 读取切向SH 波极性

归算到震源球面上的地震台站观测到的振幅大小或波形资料，含有节面离该点角距离有多远的信息，因而振幅数据比初动方向数据对震源机制解的约束作用更大［11］。因此，在实际应用中，应尽量读取震中距离较近台站的直达P、SH 和SV 波的振幅，使震源机制解反演结果更加准确可靠。在读取振幅数据前，首先也应该将地震波形缩放到合适的位置，使其易于辨认；然后在程序主窗口上方的工具栏里打开读取振幅开关按钮；最后在地震波形上用鼠标拉框选取振幅，程序会自动弹出菜单，点击相应的菜单选项即可完成对振幅数据的交互式读取。为了最大限度地减少误操作，各个方向弹出的振幅菜单中，只有量取本方向振幅的菜单选项才处于可用状态。如图5为读取垂直向直达P 波的振幅，图6为读取切向SH 波的振幅。其中，直达P 波振幅必须在垂直向读取，SH 波振幅必须在切向读取，SV波振幅可以在垂直向或者径向读取，程序在后台会进行相应的转换。为了减少反射震相的干扰，振幅读取应尽量选用震中距较近的台站，且应尽量在震相到达后的前3个周期内读取。

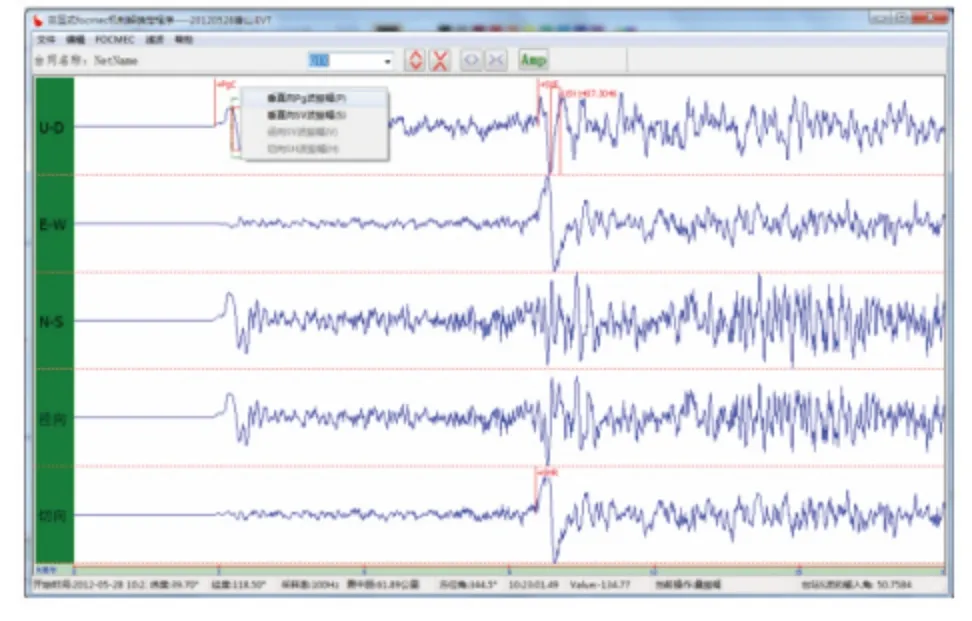
图5 读取垂直向直达P波振幅

图6 读取切向SH 波振幅

3 震源机制解反演

通过上述根据震中距的远近，交互式读取各个台站的极性和振幅数据后，即可进行震源机制解反演。点击“FOCMEC”菜单下的“震源机制解反演”菜单，即可弹出反演震源机制解的子窗口（图7）。在弹出该窗口前，程序会在后台计算每一个台站的方位角、离源角，同时把极性转换为FOCMEC 程序的约定格式；此外还将根据入射角和震中距，对每个台站的振幅比进行自由表面校正，并校正到震源球上；最后根据FOCMEC 程序的约定，生成输入文件，该步骤计算量非常大。在实际应用过程中，根据计算机的性能和台站数量，往往需要等待几秒甚至十几秒的时间。对于某一震源机制解，可计算得到任何一个台站的理论振幅比。若某台站的理论振幅比的对数与观测振幅比的对数之差的绝对值大于0.5，则认为该振幅比在反演过程中出现错误。FOCMEC法反演震源机制解需要输入可以允许的极性错误和振幅比错误数（振幅比错误数为在反演震源机制解中参与计算的振幅比出现错误的总数），以及极性是否采用相对权重等信息，震源机制解反演窗口（图7）的右上方首先会给出该地震的P、SV 和SH 波 极 性 数 量 以 及P／SV 和P／SH 振 幅 比 的 数量。在实际应用过程中，应根据这些数据来确定可以允许的极性和振幅比错误数。在震源机制解反演窗口的左侧可以输入极性是否采用相对权重、允许的极性和振幅比错误数（具体详见FOCMEC 程序包说明书［9］），然后点击“计算”按钮，即可反演得到符合允许范围的极性和振幅比错误数下的所有震源机制解的结果（图8）。图8窗口右上方表格显示每一个震源机制解结果，以及反演得到该结果的P、SV 和SH 波极性错误数、P／SV 和P／SH 振幅比的错误数量和拟合误差。其中，拟合误差是由参加反演计算的极性与振幅比数量和错误数综合得到，可以通过图8窗口右上方的表格中选取拟合误差较小的结果作为该地震最合理的震源机制解结果。该窗口的右下方给出了计算得到的震源机制解图和详细参数。如果反演的结果不理想，如允许的错误数太多，可能会导致反演结果不收敛；或者允许的错误数太少，可能会导致不能得到合适的结果。在实际应用中，可以通过反复调整左侧的输入参数（即允许的极性错误和振幅比错误数）并重新反演计算，直到得到满意的结果。

图7 震源机制解计算参数设置

图8 震源机制解计算结果

4 结束语

震源机制解能描述震源的受力和错动方式，是开展其它研究的基础资料，精确反演震源机制解是地震学研究的一项重要的日常工作。当前利用P、SV 和SH 波的初动和振幅比（FOCMEC法）是反演区域中小以上地震震源机制解的一种较好的方法，由于其操作复杂，因此推广应用具有一定的难度。本文根据FOCMEC 方法反演震源机制解的原理，结合我国保存地震波形的格式，利用Delphi面向对象语言，开发交互式反演震源机制解程序。该程序的地震波形读取与波形交互分析部分，是根据我国数字化地震波形特征以及科研人员的使用习惯单独利用Delphi语言研制。在波形交互分析后，将会在后台计算形成FOCMEC 程序的输入文件；震源机制解反演部分，则是根据Snoke等［9－10］提供的FOCMEC反演程序代码转换为Delphi代码，并实现界面化，方便操作；震源机制解显示部分，是将反演的结果利用Delphi语言将其图形化显示，方便对反演结果的准确性进行判定，同时输出详细的数据。除反演震源机制解部分是采用FOCMEC 程序代码转换为Delphi代码外，其余均是笔者编制，程序操作简单，可杜绝误操作，便于推广应用。笔者还对该程序做了非常严格的测试，并与FOCMEC 程序的计算结果进行对比，大量的测试表明该程序计算结果准确可靠。同时笔者利用该方法和程序反演了2001年以来安徽地区中等地震的震源机制解，并与其它方法或程序计算的结果进行了对比，总体认为该程序反演的结果精度较高。2012年5月28日河北唐山发生MS4.8 级地震，张杰卿等［15］利用极性法反演了该地震的震源机制解，笔者基于河北地震台网的波形资料，利用该程序共交互读取74个直达P波极性、2个SV 波极性、12个SH 波极性和15个振幅比数据，反演得到其震源机制解，并与张杰卿等［15］的结果进行对比，具体参数对比如表1所示。

表1 2012年5月28日唐山MS4.8级地震震源机制解反演结果对比

从表1可以看出，2种方法和程序反演震源机制解的结果非常接近，2个节面的走向基本相同，最大误差不超过5°。2种方法反演结果均显示该地震错动方式以走滑为主兼有一定张性分量，节面的滑动角误差不超过10°，节面倾角较大，倾向相同，倾角的误差也在可接受的范围之内，上述对比可从侧面反映程序的准确性。

我国早期的模拟地震观测资料很难进行旋转得到SV 和SH 波，但其垂直向的观测资料仍可以读取P波和SV波的极性和振幅比，因此也可以利用该方法来反演震源机制解。出于日常工作的需要，笔者在该程序的基础上，开发了手工输入模拟资料P波和SV波极性和振幅比资料反演震源机制解的程序，并作为该交互式程序的有益补充。这样不论是模拟观测，还是数字化观测，甚至二者并行运行，均可以利用该套程序来反演区域地震的震源机制解。

［1］ 张诚，曹新玲，曲克信，等.中国地震震源机制［M］.北京：学术书刊出版社，1990.

［2］ 许忠淮.用滑动方向拟合法反演唐山余震区的平均应力场［J］.地震学报，1985，7（4）：349－361.

［3］ 陈颙.用震源机制一致性作为描述地震活动性的新参数［J］.地球物理学报，1978，2（3）：39－47.

［4］ 泽仁志玛，刁桂苓，李志雄，等.大震前显示的地震震源机制趋于一致的变化［J］.地震，2010，30（1）：108－114.

［5］ 傅淑芳，刘宝诚，李文艺.地震学教程［M］.北京：地震出版社，1980.

［6］ 中国地震局监测预报司.地震参数［M］.北京：地震出版社，2003：21－22.

［7］ Kisslinger C，Bowman J R，Koch K.Procedures for computing focal mechanisms from local（SV／P）z data［J］.Bull Seis Soc Amer，1981，71（6）：1719－1730.

［8］ 梁尚鸿，李幼铭，束沛镒，等.利用区域地震台网P、S振幅比资料测定小震震源参数［J］.地球物理学报，1984，27（3）：249－256.

［9］ Snoke J A，Munsey J W，Teague A G，et a1.A program for focal mechanism determination by combined use ofpolarity and SV－P amplitude ratio data［J］.Earthquake Notes，1984，55（3）：15－20.

［10］ Snoke J A.Earthquake mechanism［M］／／James D E.Encyclopedia of Geophysics.New York：Van Nostrand Reinhold Company，1989：239－245.

［11］ 刘杰，郑斯华，康英，等.利用P波和S波的初动和振幅比计算中小地震的震源机制解［J］.地震，2004，24（1）：19－26.

［12］ 倪红玉，刘泽民，沈小七，等.利用FOCMEC方法计算震源机制解的影响因素分析［J］.华北地震科学，2011，29（3）：1－7.

［13］ 笠原庆一.地震力学［M］.北京：地震出版社，1984：28－49.

［14］ 刘泽民，徐鑫，夏仕安，等.体波谱振幅相关系数计算程序的开发与实现［J］.地震地磁观测与研究，2011，32（5）：148－152.

［15］ 张杰卿，邵永新.2012年5月28日河北唐山4.8级地震分析［J.华北地震科学，2013，31（1）：34－37.