地震动输入界面处剪切波速对加速度峰值的影响

李建亮，李福海，亢川川，赵 晶，何玉林

（1.四川省地震局，成都 610041；2.西南交通大学，成都 610031）

0 引言

地震动加速度峰值是场地设计地震动参数的重要参数之一，它包括地表以及工程建设所要求深度处的数值，合理的加速度峰值是得到工程抗震设计中合理的地震动输入的必要条件之一，而合理的地震动输入既是工程结构抗震设计分析的基础，又是保证建筑结构抗震设计可靠与经济性的重要条件之一。

土层地震反应计算的计算结果之一即是加速度峰值。土层地震反应分析计算模型参数的确定是土层地震反应计算的关键问题，模型参数包括土层厚度、密度、剪切波速、土动力学非线性参数以及地震动输入面。其中土层厚度、剪切波速和土动力学非线性参数对地表设计地震动参数的影响已有较多的学者进行了研究［1－9］，但地震动输入界面处剪切波速变化对地表及工程建设所要求深度处的加速度峰值的影响还鲜有学者研究［10－11］。国家标准《工程场地地震安全性评价》（GB17741－2005）中规定，在进行土层地震反应计算确定地震输入界面时，Ⅰ级工作应采用剪切波速不小于700m／s的土层顶面作为地震动输入面，Ⅱ级工作应采用剪切波速不小于500m／s的土层顶面作为地震动输入面。至于为什么这样选择，该国标及其宣贯教材中均未作解释说明。只是在宣贯教材中这样描述“不同级别的工作，地震动输入面确定的要求有所不同”，“700 m／s和500m／s的剪切波速值相当于一般性基岩和坚硬土层的经验波速值”。本文选取成都平原地区某住宅项目的一个典型钻孔剖面，建立土层地震反应计算模型，通过改变地震动输入界面处的剪切波速值，分别进行土层地震反应计算，对计算结果进行分析研究，得出地震动输入界面处剪切波速对加速度峰值的影响规律，以期对能够更深层次的理解上述规定提供有益的帮助。

1 计算分析方法

采用《工程场地地震安全性评价》（GB17741－2005）推荐使用的一维土层地震反应计算的等效线性化波动方法，使用中国地震局组织鉴定验收的ESE软件作为计算程序［12－14］，进行场地土层地震反应分析计算。

2 土层地震反应计算模型

该工程场地钻探揭露的地层从上至下依次为杂填土、粉质粘土、中砂、松散卵石、稍密卵石、中密卵石、密实卵石（表1），为成都平原地区具有代表性的卵石场地剖面。该项目拟采用天然地基方案，以松散卵石层为基础持力层，基坑开挖深度为5 m。故在进行工程抗震设计时不仅需要工程场地地表处的加速度峰值，同时还需要基坑开挖深度（地下5 m）处的加速度峰值。我们选取的该典型钻孔剖面的土层地震反应计算模型参数见表1。计算中的粉质粘土的动力非线性关系（动剪切模量比与阻尼比参数）由中国科学院水利部成都山地灾害与环境研究所测试，其它土类的动力非线性关系参考了《四川数字强震动观测网络建设》和《土壤的动剪切模量和阻尼比》［15］中的实验结果（表2）。

表1 钻孔剖面的土层地震反应计算模型参数

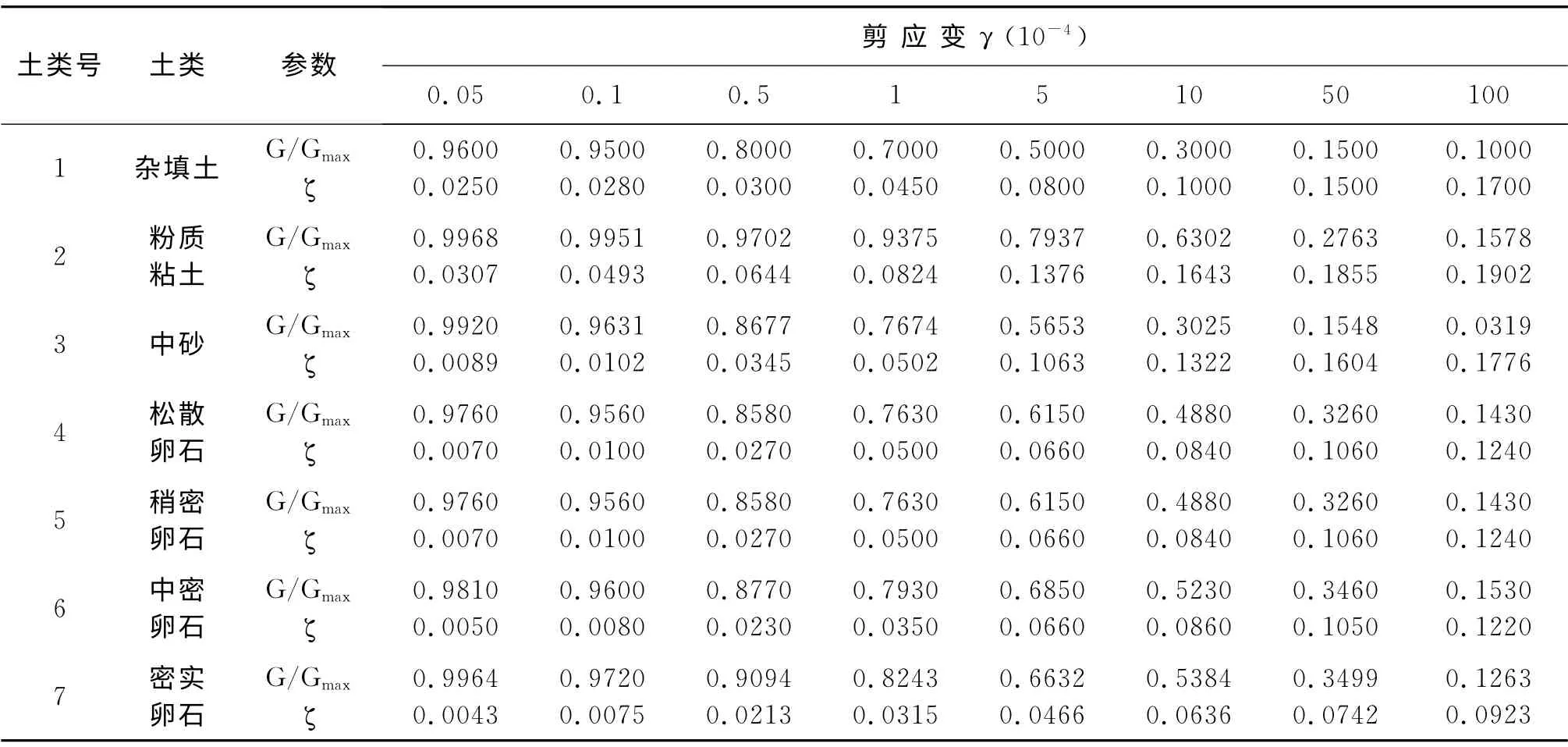
表2 各土层的动剪切模量比及阻尼比与剪应变的关系

3 基岩输入地震动

根据国标《工程场地地震安全性评价》的规定，依据对成都某住宅项目区域及近场地震活动性和地震构造背景的研究，确定了用于该钻孔地震危险性分析计算的地震带、地震构造区以及潜在震源区的地震活动参数。并利用适合于本区域的地震动衰减关系，采用中国地震局推荐的地震危险性分析程序包，计算得到了钻孔剖面场地在50年超越概率63%（小震）、10%（中震）、2%（大震）水平下的基岩峰值加速度及基岩加速度反应谱。计算结果见图1。

图1 场地基岩加速度反应谱图（5%阻尼比）

以地震危险性分析得到的基岩加速度反应谱作为目标谱，采用随机相位差和适合本地区的时程强度包络函数，用人工数值模拟的方法合成基岩地震动时程，作为土层地震反应分析计算的基岩输入地震动。在拟合地震动时程时，为了考虑相位随机性的影响，对不同概率档的目标反应谱，即大震、中震、小震的目标谱，分别合成3条地震动时程作为同一剖面计算模型的地震动输入。

4 研究方案

《工程场地地震安全性评价》（GB17741－2005）中规定，Ⅱ级工作（此住宅项目的工程场地地震安全性评价为Ⅱ级工作）在进行土层地震反应分析计算选取地震动输入面时，应采用下面3种情况之一：①钻探基岩面；②剪切波速大于或等于500m／s土层顶面；③钻探深度大于100 m 时，剪切波速有明显跃升的土层分界面或者用其他方法确定的界面。根据表1中计算模型的数据，采用②规定确定密实卵石层顶面为地震动输入界面。应该注意到地震动输入面是假想的弹性均匀基岩空间和非均匀土层的交界面，从场地地层剖面图或钻孔柱状图中可以看出，该交界面为一条线，而非整个计算基底层。然而波速测试报告中提供的计算基底层的剪切波速值为该层的平均波速值，而非该层顶面处的波速值。该平均波速值大于土层顶面处的波速值，这样在进行土层地震反应计算时，输入界面处的剪切波速值就变大了，这将会对场地地表和地下5m 处的地震动加速度峰值产生影响。本文将通过改变地震动输入界面处的剪切波速值，来研究地表和工程建设所要求深度（地下5m）处加速度峰值的变化规律。我们将输入界面处的剪切波速值依次从500m／s增加至800m／s，数值间隔 为50 m／s，即500 m／s、550 m／s、600 m／s、650m／s、700m／s、750m／s、800m／s。

5 计算结果及分析

利用人工合成的不同超越概率（大震、中震、小震）下的各3条基岩地震波，将幅值缩小一半后作为输入地震波，对场地剖面进行了地震反应计算，得到了在各个输入界面波速值下的地表处和地下5 m处的加速度峰值，计算结果见表3、表4。

表3 地表处的加速度峰值

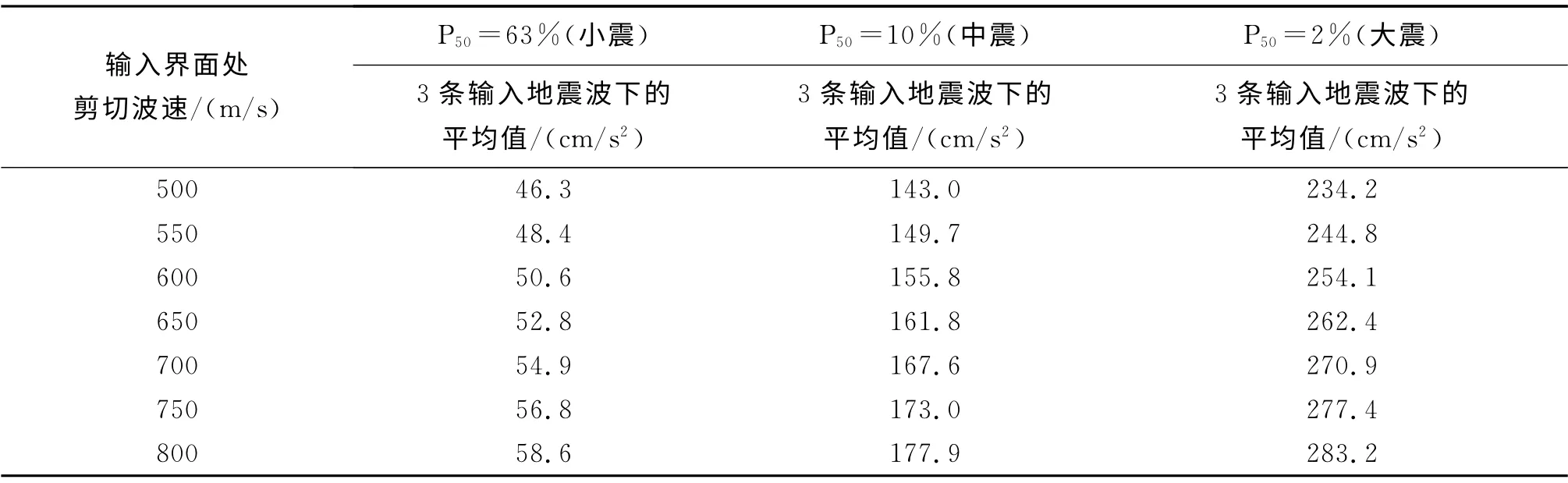
表4 地下5m 处的加速度峰值

从表3和表4中可以看出，地表处和地下5m处的加速度峰值与地震动输入界面处的剪切波速值成正相关关系，即随着剪切波速值的增大而增大。每次增加输入界面处的剪切波速值后计算所得到的加速度峰值，与用初始剪切波速为500m／s时计算所等到的加速度峰值相比，增大的百分比见表5和表6。

表5 地表加速度峰值比初始计算值增大的百分比

表6 地下5m 处加速度峰值比初始计算值增大的百分比

从表5和表6中可以看出，在小震地震动输入下，地表和地下5m 处的加速度峰值增大百分比的最大值分别为32%和27%；在中震地震动输入下，地表和地下5 m 处的加速度峰值增大百分比的最大值分别为26%和24%；在大震地震动输入下，地表和地下5m 处的加速度峰值增大百分比的最大值分别为22%和21%。

为进一步分析其变化规律，我们利用Excel中添加趋势线的方法，得到了表3和表4中数据的拟合回归方程，并给出了方程的拟合系数、决定系数R2以及它们的适用范围。R2称为方程的决定系数（或确定性系数），表示方程中自变量对因变量的解释程度。R2取值在0到1之间，越接近1，表明方程中自变量对因变量的解释能力越强。通过对比多种统计模型，发现当采用对数回归模型时，二者的拟合关系非常好，R2数值达到0.99以上。故我们选取了对数模型作为经验回归公式（图2和表7）。

进一步分析图2和表5～表7 可以发现，无论是地表处的加速度峰值，还是地下5m 处的加速度峰值，在相同的地震动输入强度下（例如同是小震作用下），均随着输入界面处的剪切波速的增大而呈对数形式增大。运用表7中的拟合方程，并结合表5和表6的计算结果，可以得出地表和地下5m 处的加速度峰值随剪切波速增大的速率是随着输入强度的增大而变小，即相同的波速增大量，小震输入下的加速度峰值增加速率最大，中震输入下的增加速率次之，大震输入下增加的速率最小。且在相同的地震动输入强度下，地下5m 处加速度峰值随剪切波速增大而增加的速率小于地表处。

6 结语

本文利用目前工程上广泛应用的土层地震反应计算分析软件对成都平原地区某典型卵石场地进行了分析计算，得到了不同输入强度下的地表和地下5m 处加速度峰值随输入界面处剪切波速值增大的变化规律。无论是地表加速度峰值，还是地下5 m处的加速度峰值，在相同的地震动输入强度下，均是随着输入界面处剪切波速值的增大呈对数形式增大，且在小震输入下的增加速率最大，中震输入下的增加速率次之，大震输入下增加得最慢，但地下5m处的加速度峰值的增加速率小于相应变量下的地表处的加速度峰值的增加速率。当地震动输入界面处的剪切波速值从500m／s增加至800m／s时，地表处和地下5m 处的加速度峰值均增大了20%以上，最大达到了32%。若按800 m／s的计算结果进行工程抗震设计，便大大增加了工程建设项目的成本。因此，我们建议国家标准《工程场地地震安全性评价》（GB17741－2005）在规定地震动输入界面处剪切波速值下限（最小值）的同时，也要规定其上限（最大值），以期得到合理可靠并兼顾经济性的工程抗震设计结果。文中统计得到的加速度峰值与输入界面处剪切波速值间的经验关系式可作为本地区具有相似场地条件工程换算加速度峰值的经验公式，为工程抗震设计人员提供参考。

［1］ 刘红帅，薄景山，吴兆营，等.土体参数对地表加速度峰值和反应谱的影响［J］.地震研究，2005，28（2）：167－171.

［2］ 王绍博，丁海平.土动力参数对土层动力反应的影响［J］.地震工程与工程振动，2001，21（1）：105－108.

［3］ 高玉峰，刘汉龙，朱伟，等.剪切波速对砂土层地震反应的影响［J］.工程勘察，2001，（1）：39－42.

［4］ 李建亮，亢川川，何玉林，等.场地条件对地面加速度峰值离散性的影响研究［J］.震灾防御技术，2011，6（4）：416－426.

［5］ 兰景岩，薄景山，吕悦军.剪切波速对设计反应谱的影响研究［J］.震灾防御技术，2007，2（1）：19－24.

［6］ 薄景山，李秀领，刘红帅.土层结构对地表加速度峰值的影响［J］.地震工程与工程振动，2003，23（3）：35－40.

［7］ 兰景岩，刘红帅，吕悦军，等.表层土剪切波速的不确定性对地表设计谱平台值的影响［J］.吉林大学学报（地球科学版），2012，42（3）：770－776.

［8］ 吕国军，田丽，张合，等.土层动力参数变化对地表地震反应影响的研究［J］.华北地震科学，2013，31（2）：18－22.

［9］ 曹均锋，冯伟栋，孟凡月，等.剪切波速对场地地表地震动参数的影响［J］.震灾防御技术，2013，8（3）：252－260.

［10］ 施春花，吕悦军，彭艳菊，等.地震动输入界面的选取对地震动参数的影响［J］.中国地震，2009，25（3）：282－293.

［11］ 王冲，薄景山，齐文浩，等.输入界面对地表加速度峰值的影响［J］.地震工程与工程振动，2011，31（6）：55－61.

［12］ GB17741－2005工程场地地震安全性评价［S］.北京：中国标准出版社，2005.

［13］ 廖振鹏，李小军.地表土层地震反应的等效线性化解法：地震小区划［M］.北京：地震出版社，1989：141－153.

［14］ 胡聿贤.地震安全性评价技术教程［M］.北京：地震出版社，1999.

［15］ 石兆吉.土壤的动剪切模量和阻尼比［C］／／地震小区划（理论与实践）.北京：地震出版社，1989.