我国城镇化背景下居民收入差距对消费的影响研究——基于动态面板数据模型的估计

杨 勇

(1．天津大学管理与经济学部，天津300072;2．天津职业技术师范大学经济与管理学院，天津300222)

当前，我国正进一步推进城镇化建设，基于目前国有企业进一步发展促使部分企业进行改革改制现状所导致的社会的激烈竞争，城镇的就业形势也愈发严峻，随着农民工的大规模涌入，城市失业人员的数量持续增长，比例也越来越高。在这个过程中收入低和靠失业金生活的人群的数量就更多，逐渐地城市中出现了一个相对贫困的群体。这个群体使城镇居民之间的收入差距越来越大，这个水平比城乡之间居民的收入差距明显更大［1］。同时，我国城镇居民存在消费需求不振的问题，而消费不振与我国城镇居民收入差距扩大之间是否存在一定的联系，正被越来越多的专家所关注与探讨。

从经济学角度出发，城镇居民的消费问题正成为国家与社会普遍关注的问题，根据相对收入假说消费理论，消费具有不可逆性，当期的消费除了受到当期收入等因素的影响外，还被前一期消费水平影响。相对收入假说认为，收入水平是决定消费支出的主要因素。相对收入包括两层含义:一是强调较之前收入增长的消费者所组成的消费群体和消费集团二者均对低收入个人和群体的消费行为有示范性和攀比性;二是强调过去高峰收入时期对当前收入所产生的消费影响。该假设认为，现期消费支出很大程度上受过去的高峰收入的影响:消费支出随收入提高而提高，但只能随收入减少而有限地减少，形成“自上不能下”的棘轮效应［2］。当前，研究城镇居民收入对消费影响的主要方法是因子分析法和协整分析法，但这两种方法存在一定的不足。动态面板数据模型的使用，实现了在某种程度上弥补以上两种方法的局限性，即可以在不同的时间点上选择不同的居民收入数据作为样本来进行观测。这一方法的使用，既实现了对不同的城镇居民在收入方面的不同进行分析，且对消费受居民收入不同的影响进行了分析。本文通过对城镇居民消费的动态面板数据模型的分析，重点考察了城镇居民收入差距对消费的影响和消费的“棘轮效应”［3-4］。

一、固定效应动态面板数据模型及估计

截面个体变截距动态面板数据模型表达式为［5］

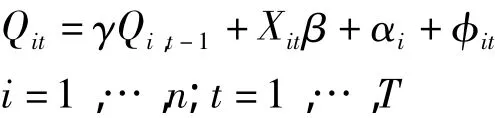
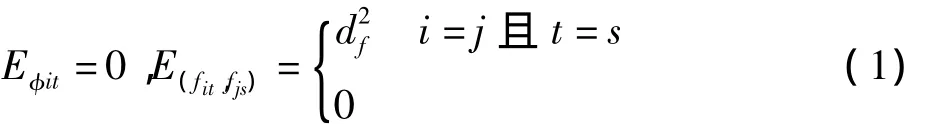
将滞后被解释变量作为解释变量引入模型，得出

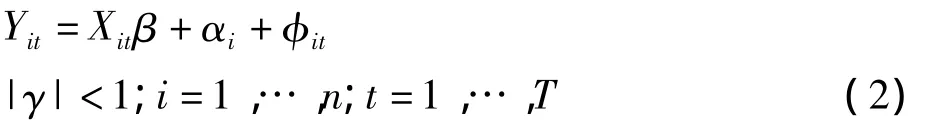
1．不包含外生解释变量的动态面板数据模型估计

首先考虑不包含外生解释变量的截面个体变截距动态面板数据模型

如果φit是正态分布，且Yi0是具体的给定常数C，则式(4)的MT估计在T较小时是存在偏估计的。则对于截面个体相关的估计模型，T固定不变、n→∞时与γ估计一致。得

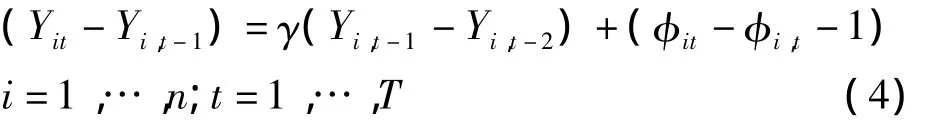
进一步把(Yi，t-2-Yi，t-3)作为(Yi，t-1-Yi，t-2)的工具变量，得

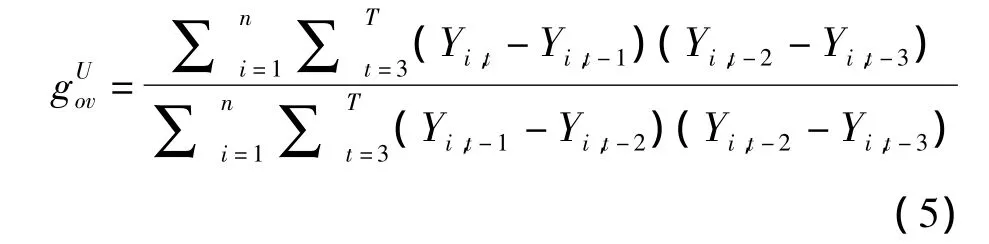
把 Yi，t-2作为(Yi，t-1-Yi，t-2)的工具变量，得

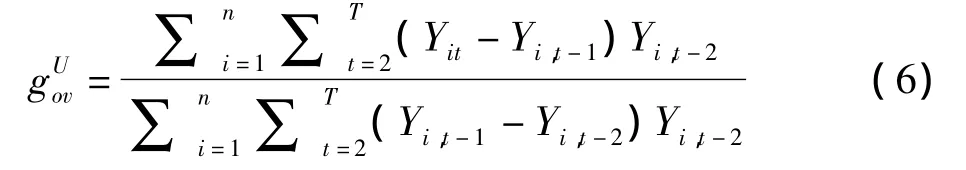
当n→∞或者T→∞时，式(6)、(7)都与γ参数估计一致。则

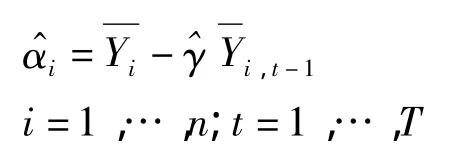
得出式(4)的参数估计。

2．包含外生解释变量的动态面板数据模型估计

在包含外生解释变量的情况下，截面个体变截距动态面板数据模型为

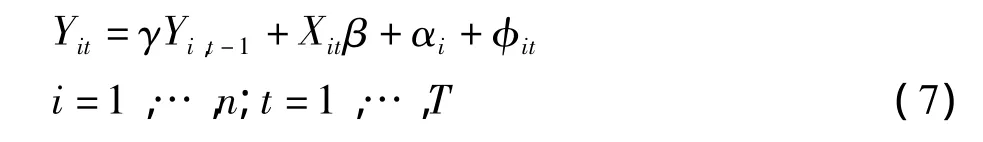
同理，采用工具变量方法估计差分模型，得γ和β的一致估计量，然后求出αi的估计量。

二、随机效应动态面板数据模型及估计

1．随机效应动态面板数据模型的建立

如果式(8)中的αi为随机变量，可将式(8)写为

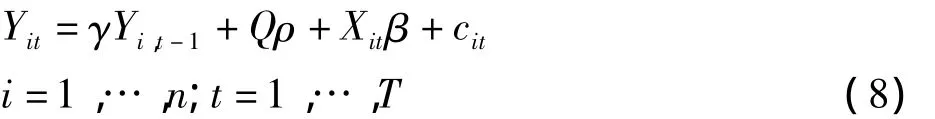
式中:Qi是不随时间变化的1×H1阶属性外生变量向量;Xit是随时间变化的1×H2阶外生变量向量，且使它的第一个元素为1，表示为随机效应变截距中不变的主体部分，得出变截距为(β1+αi);cit=αi+φit;γ是1×1阶，ρ和β分别表示H1×1阶和H2×1阶的参数变量［6-7］。

这里，Yi0随机，即假定Yi0是均值为φy0，方差为的随机变量，表示为Yi0=φy0+εi。该假设的合理性在于人们只会关心达到目的的状态结果，不会关心是如何达到这种初始状态的，只需要这种分布的结果具有有限的均值和方差［8］。

2．随机效应动态面板数据估计

假定αi和φit服从正态分布，初始条件的不同假定存在着不同的似然函数［9］。

(1)Yi0固定下的似然函数为

(2)Yi0随机独立于αi的似然函数为

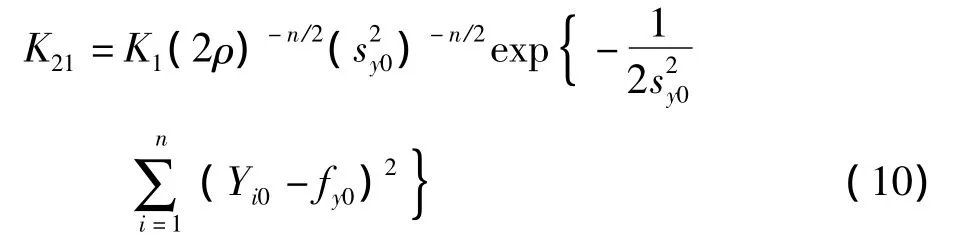
(3)Yi0随机，与αi相关的似然函数为

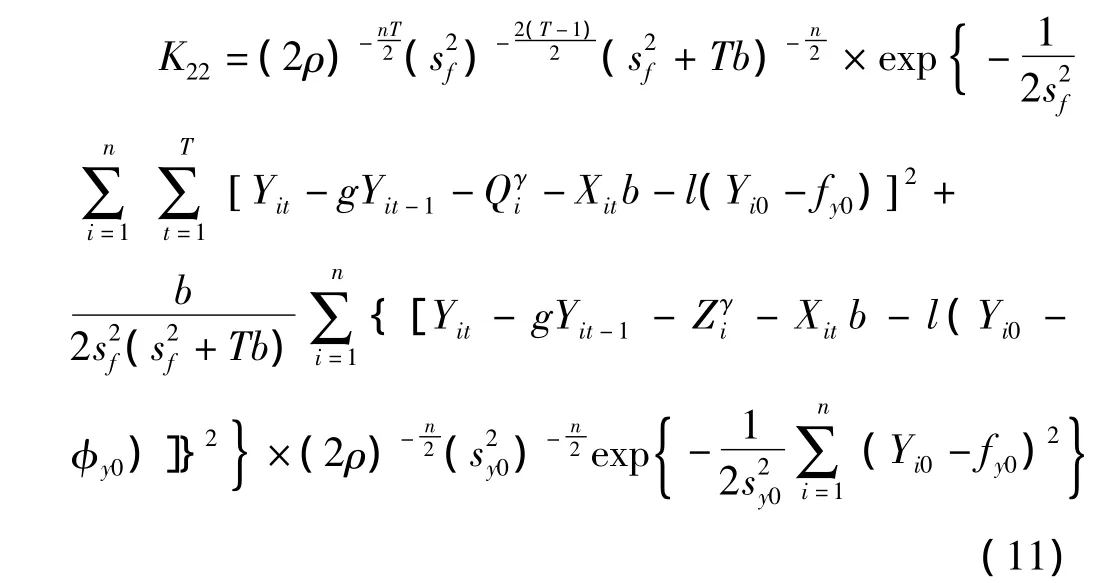
使似然函数达到最大化，可得到相应条件下的参数的最大似然估计。

3．随机效应动态面板工具变量估计

当横截面个体数目较多、时间的长短又不太确定时，初始条件不同的情况下似然函数不同，所以初始条件的选择是至关重要的，错误的选择将导致得到的估计与正确的估计偏离，不是一致估计，所以选择工具变量估计，步骤如下［10-11］。

步骤1:对式(9)差分，得

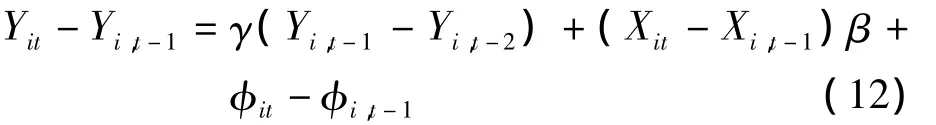
利用 Yi，t-2和(Yi，t-2-Yi，t-3)作为(Yi，t-1-Yi，t-2)的工具变量，并且得到γ和β的估计γ和β。

步骤2:把估计出的γ和β代入式(12)在时间上求出平均的方程，得

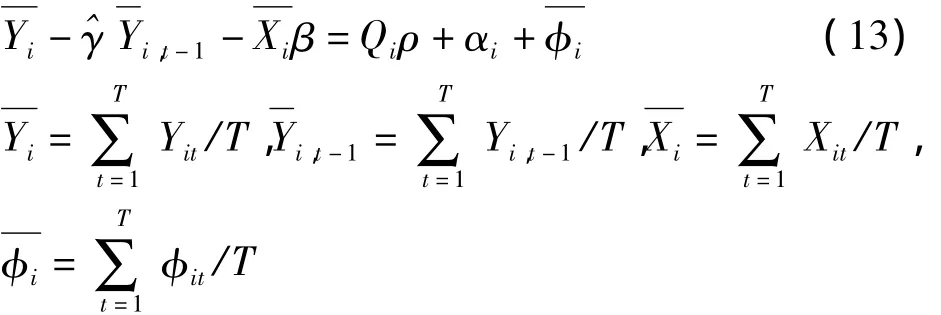
式(13)根据最小二乘法，得到ρ的估计ρ。

步骤 3:估计 σ2φ和 σ2α，得

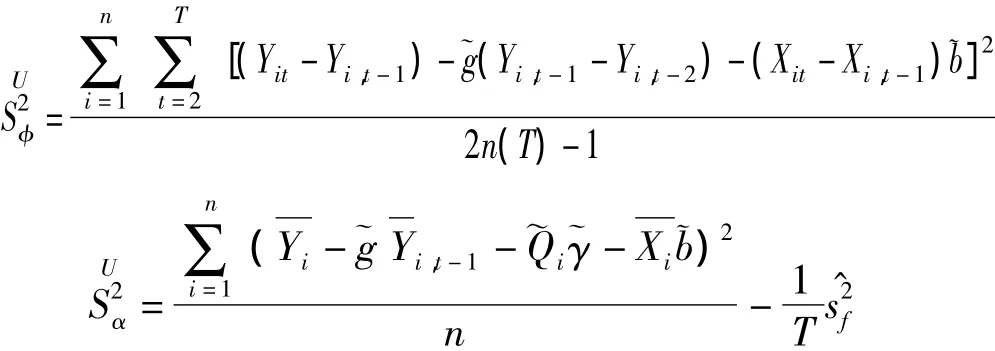
上式中的估计与初始值Yi0无关。当n或T趋向于无穷大时，γ、β和σ2φ估计是一致;只有当n趋向于无穷大时，ρ和σ2φ的估计才是一致。

三、实证分析

本文以2006—2011年我国24个省市自治区的城镇居民消费情况为例进行实证分析，数据来自相关统计年鉴。另外，所选取的各个地区的数据是在以2005年为基期的城镇居民收入数据的基础上进行了平减以消除消费变化的影响。由于2006—2011年期间，城镇居民的收入和物价水平波动较大，因此将城镇居民的收入水平和消费状况进行适当的调整，对其各时期收入与消费价格指数进行平减，并以实现居民的经济性和理性消费为目标，建立模型分析预测值和真实值是否吻合。

1．动态面板数据模型估计

考察城镇居民收入差距对消费的影响和消费的“棘轮效应”，建立关于城镇居民消费的动态面板数据模型。总体回归模型设定为

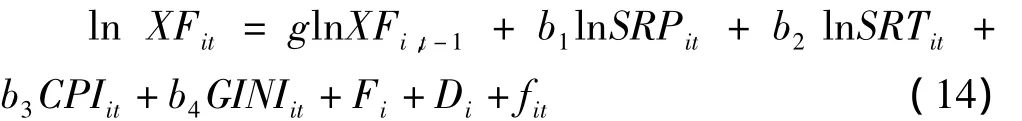
式中:ln XFi，t、ln XFi，t-1分别代表第 i省 t时期和 t-1时期城镇居民的消费自然对数;ln SRTit分别表示第i省t时期的城镇居民持久收入和暂时收入的自然对数;CPIit作为第i省t时期的消费价格指数;以GINIit作为第i省t时期城镇居民的基尼系数衡量城镇居民收入差异;而Fi代表第i省的固定效应或随机效应水平，以反映那些因地区差异而对消费有显著影响但其本身很难量化的影响因素;Di则为时间虚拟变量，其作用为反映各省随时间而变化的因素对消费的影响;以φit代表第i省t时期的随机误差项。

通过Hausman检验，选取了固定效应的变截距模型［8］。并选用 ln XFi，t-2和 ln XFi，t-3作为解释变量 ln XFi，t-1的工具变量。通过广义矩估计方法得到如下估计方程，其中括号内的数值代表t检验统计量，J统计量表明这两个工具变量的有效性。

动态模型的截距估计值如表1所示。

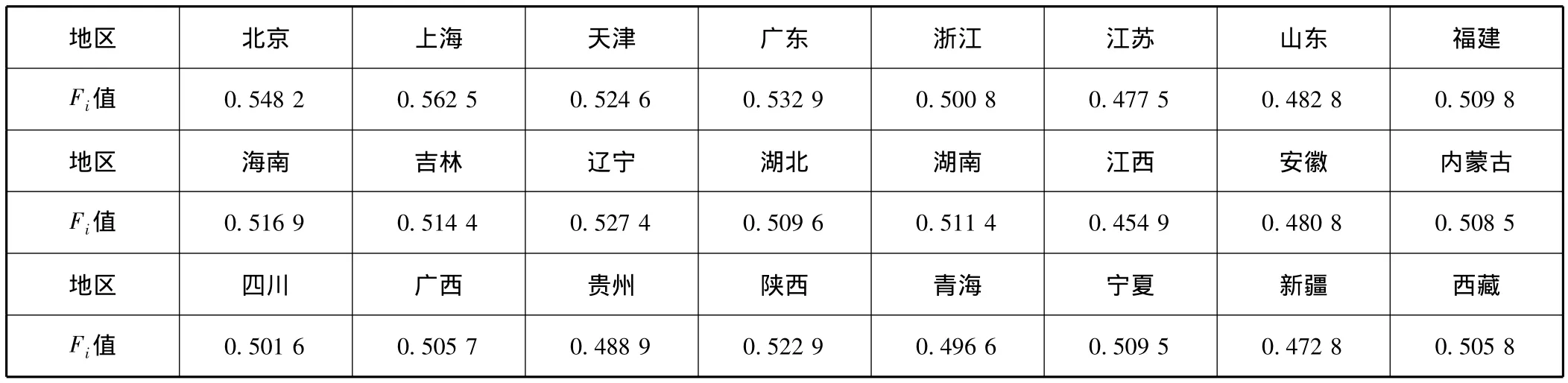
表1 动态模型变截距Fi的估计值

以上动态面板数据模型估计结果表明，消费的“棘轮效应”显著，当期消费很大程度上受滞后一期的消费的正向影响。从数量上看，城镇居民前期消费每增长1%，引起当期消费平均增长0．521 8%;居民消费的持久收入弹性和暂时收入弹性分别为0．332 5和0．011 7;收入差距对消费影响显著，城镇居民基尼系数的绝对值每增加1%，消费平均将减少约0．35%。

2．静态变截距面板数据模型估计

如果不考虑消费的“棘轮效应”，建立静态变截距面板数据模型。总体回归模型设定为

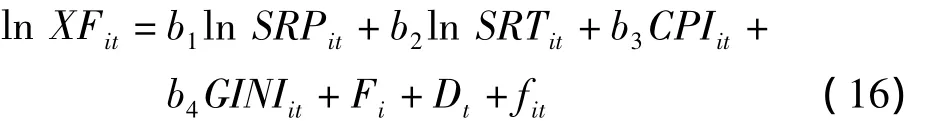
通过Hausman检验，选取了固定效应的变截距模型。得到估计方程

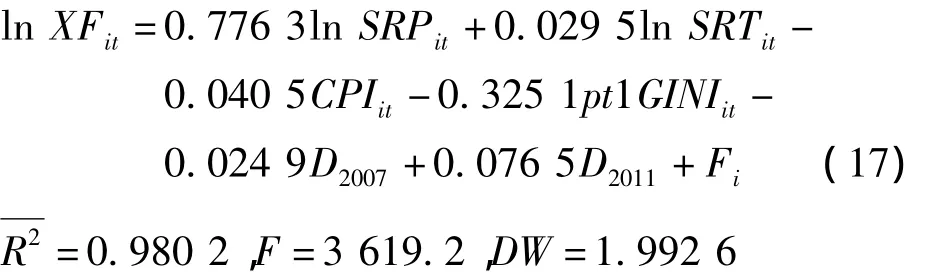
静态模型的截距估计值如表2所示。

表2 静态模型变截距Fi的估计值

以上静态变截距面板数据模型估计结果表明，居民消费的持久收入弹性和暂时收入弹性分别为0．776 3和0．029 5;收入差距对消费有显著影响，城镇居民基尼系数的绝对值每增加1%，消费平均将减少约 0．33%。

将式(14)和式(16)对比发现，由于在动态模型中引入了前期消费ln XFi，t-1作为解释变量，引起了其他解释变量的系数在两个模型中的较大差异。ln XFi，t-1与其他解释变量之间存在统计相关性。从另一方面讲，前期消费对当期消费的影响，也就是“棘轮效应”并不是直接的，而是间接的，是通过改变当期收入等因素而影响的。动态面板数据模型估计结果反映出了各个变量之间的经济关系的定量解释，城镇居民消费的持久收入弹性和暂时收入弹性分别为0．332 5和0．011 7;城镇居民基尼系数的绝对值每增加1%，消费平均将减少约0．35%等，都是不可靠的。

四、结 语

对动态面板数据模型和静态变截距面板数据模型的对比分析，可以看出2006至2011年间我国各地区的城镇居民收入与消费之间存在着动态均衡机制的内部关系，当期或者后期的消费水平将一定程度上受不同地区城镇居民收入的差异所影响，这些是与城镇居民的收入水平呈正相关的。所以，城镇居民的收入水平一定程度上可以作为调控城镇居民消费的主要工具。各个地区之间的分配差距缩小将一定程度上推动我们国家消费市场和消费结构的关键要素。作为政府应该扩大在其他方面的投资，调整这个方面的关键，一定程度上缩小各个地区在分配方面的差距，并下大力度推动经济的发展，推动就业率的提升，用多方面、多渠道的方法推动居民收入的提升，用各种方式缩小各个地区的收入水平和贫富差距，进而让全国各地区的人民的消费结构更加的合理。

［1］李雄军，曹 飞．扩大居民消费的税收政策探讨:以金融为视角［J］．税务与经济，2012(3):93-96．

［2］李 武．基于凯恩斯消费函数的我国城乡居民消费差异实证分析［J］．统计研究，2007(6):67-69．

［3］罗 芳，韩玉香．浅谈我国城镇居民收入分配差距对消费的影响［J］．时代金融，2012(11):65-67．

［4］王 怡，李树民．城镇居民消费结构与经济增长关系的实证研究［J］．统计与决策，2012(10):133-135．

［5］李子奈，叶阿忠．高等计量经济学［M］．北京:清华大学出版社，2000:127-148．

［6］洪永淼．高级计量经济学［M］．赵西亮，吴吉林，译．北京:高等教育出版社，2011:136-168．

［7］孙 凤，易丹辉．中国城镇居民收入差距对消费结构的影响分析［J］．统计研究，2000(5):9-15．

［8］曹崇延，李 娜．我国证券投资基金持股与股价波动的关系:基于动态面板数据模型的实证研究［J］．西安电子科技大学学报:社会科学版，2008(3):98-102．

［9］Murray M P．Econometrics:A Modern Introduction［M］．Upper Sandle River:Prentice Hall，2006:286-338．

［10］Chen K，˙Imrohoroˇglu A，˙Imrohoroˇglu S．The Japanese saving rate between 1960 and 2000:Productivity，policy changes，and demographics［J］．Economic Theory，2007，32(1):87-104．

［11］Sommer M．Habit formation and aggregate consumption dynamics［J］．The BE Journal of Macroeconomics，2007，7(1):1935-1690．