复杂系统脆性视角下的公共危机预控研究
李祥飞,阎耀军(天津工业大学公共危机管理研究所,天津300387)
复杂系统脆性视角下的公共危机预控研究
李祥飞,阎耀军
(天津工业大学公共危机管理研究所,天津300387)
摘要:公共危机事件具有不确定性,发展途径和演变不规律性,事件之间的复杂联系使得公共危机事件产生的影响易形成连锁反应,对社会稳定产生巨大的冲击,如何预测和控制公共危机事件的影响是应急管理的重要方向之一。文章从复杂系统脆性的视角出发,将社会系统视为一个由若干子系统构成的复杂系统,探讨了公共危机事件可能导致的子系统之间发生的崩溃模式和演化机制,并进行了模拟,最后提出基于支持向量机的预警方法。研究结论可以为建立健全公共危机预警系统提供参考。
关键词:复杂系统;脆性;公共危机;预控
我国处于社会发展的转型期,社会风险和危机也处于高发期。各类危机事件的频频发生很可能会发展并演变为严重威胁社会公共安全的重大危机事件;同时,来自非传统安全领域的经济安全、信息安全、生物安全、防恐反恐等问题也日渐突出。危机事件的发生和处理已经成为社会各界广泛关注和讨论的问题[1]。然而,公共危机事件的发生往往具有不确定性,发展途径和演变具有不规律性,即使是细小的事件如果无法得到有效的化解则很可能衍生出一系列新的事件,以至于对整个社会的稳定造成巨大的影响[2]。因此,如何有效控制公共危机事件的影响范围,是降低损失的重要途径,也是应急管理研究中非常重要的课题之一[3]。
本文以系统论为基础,从复杂系统的脆性特性出发,探讨了公共危机事件发生以后演变过程造成的与其他子系统事件的崩溃机理,并在此基础上提出了利用三维元胞自动机进行模拟和仿真,最后提出了预测和预警方法,从而为有效控制危机事件的不良影响扩散提供了参考和借鉴。
一、复杂系统崩溃机理
人类社会实际上是一个复杂的巨系统,而且具有一般复杂系统的开放、多层等特征,更具有明显的复杂性特征,因此在分析复杂系统的时候可以将其视为一系列子系统的有机组合。复杂系统如果受到强大的外力干扰很可能会发生崩溃,而这种崩溃的发生是以子系统发生崩溃为前提的,因此对于复杂系统进行分析要着重探讨子系统发生崩溃的机理,同时理清子系统之间崩溃的传导机制。复杂系统的脆性理论提出为解决公共危机预警研究提供了新的解决思路[4]。其基本思想有三个:1)假设有一个完整的系统,当它的某个子系统受到外界的强大干扰时会改变其原来的有序状态,随后会与其他相邻的子系统进行物质、信息或者能量上的置换,进而导致其他子系统的无序。当它的无序状态对其相邻的子系统的有序状态造成足够大的影响时会导致相邻子系统的崩溃。按照这种规律演化,子系统发生崩溃会进行扩散,当全部子系统崩溃时会造成整个系统的崩溃。2)子系统之间存在脆性联系熵,熵主要有正熵和负熵两种方式,当某个子系统受到外力干扰时其正熵值会显著增大,因此会汲取环境中的负熵对其进行中和,当负熵无法达到中和的需求时子系统的无序状态会更加严重,当达到一定的程度时便会发生崩溃。3)子系统之间的关系是非合作的,因为各个子系统需要汲取负熵来中和其无序状态,而负熵一般是有限的,当几个子系统为争取有限的负熵资源时就会发生非合作博弈的行为。
图1中的熵值代表系统的状态函数。到目前为止,熵的研究主要有热力学熵和信息熵两种,这两种类型的熵值都出现在物理学领域。热力学熵是由克劳修斯提出来的,具体指的是系统的一种状态函数,用来衡量热力学系统的无序程度。随后,玻尔兹曼提出了热力熵的函数式:S=klnω,其中k为常数,ω为状态含量。信息熵的提出是由香农和维纳在热力学熵的基础上提出的,具体而言就是将信息看作未知量,当信息越无序则熵值越大,对其进行测定就越困难。具体的测定方法是设系统包括n个不相容事件,其概率值分别为Pi,且满足概率和为1。衡量系统的信息不确定性可以用U(P1,P2,…,Pn)表示,具体计算式为
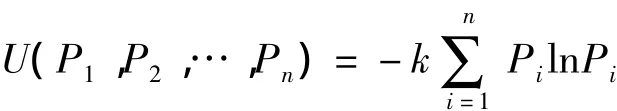

图1 子系统之间脆性熵的形式
通过对上面两种熵的描述可以发现,熵值可以定义为系统的一种状态函数,是对其无序程度的度量。因此,熵的引入对于研究复杂系统的无序程度具有重要的意义[5]。公共危机领域具有复杂系统的特性,因此熵可以用来衡量各个子系统之间联系的无序程度。那如何通过研究子系统之间的行为判定一个完整系统发生崩溃的可能性呢?从复杂系统脆性理论的观点来看,系统之间的关联性可以用“脆性”来衡量。脆性程度越强则受到来自于其他系统的干扰进而发生崩溃的可能性就越大。为了更加直观地了解脆性这个概念,本文利用三维元胞自动机对复杂系统之间的脆性进行模拟和仿真。
二、三维元胞自动机的复杂系统脆性模拟
系统的崩溃形式是多种多样的,当一个系统崩溃对另外子系统产生影响的作用方式也必然不一样,根据集对理论可以将子系统之间的影响方式划分为同一性、波动性和对立性。即对两个子系统之间建立同、反、异的关联方式度量公式:ζ=α+βI+γJ,α为同一性测度,β为差异性测度,γ为对立性测度,其中有I∈[0,1],J∈[-1,0]。如此,当一个子系统X在干扰下发生崩溃,则另外一个子系统的状态向量中至少会有一个yj(1<j<n)与子系统X发生脆性联系,假设这三类发生的概率分别是Pα(yj/X)、Pβ(yj/X)、Pγ(yj/X),且满足Pα(yj/X)+Pβ(yj/X)Pγ(yj/X)=1,则三类熵值的表达形式为[4]

实际情况下,系统受到的外力具有较强的不确定性,且不只一方面,因而系统的状态就具有较强的不确定性,发生崩溃的可能性也不一样。假设系统受到不同作用力时的脆性熵形式为
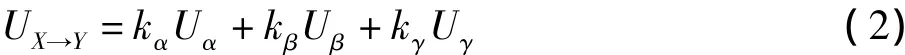
式中kα,kβ,kγ分别为三种熵的权重。基于此,一定存在一种组合使得熵值UX→Y最大,在这种状态下X崩溃后对Y产生的干扰最大,也就是说两者之间的脆性关联最大[6-7]。基于这样的系统崩溃机理,本文采用元胞自动机进行模拟演示[8-9]。比较传统的研究方法是利用元胞自动机研究两个相连个体的运动规律。考虑社会系统的复杂性,子系统之间的联系应该更为紧密,因此为了更加直观地模拟,本文采用三维元胞自动机进行模拟。如图2和图3所示,假设不从外界补充任何的负熵,选用一个长宽高各5个元胞组成的立方体代表研究的整个系统,这个系统由125个子系统组成。立方体代表该子系统受到“冲击”后发生崩溃,随后的一系列变化代表该系统的崩溃路径,其中缺失的元胞代表其已经发生崩溃。以下模拟了系统中两种位置的子系统发生崩溃时的不同演化模式。
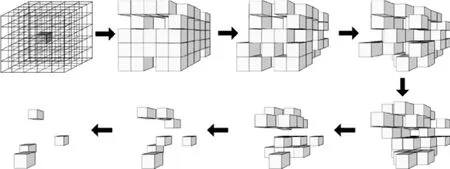
图2 中间位置的三维元胞自动机系统崩溃模拟
从三维元胞自动机的模拟情况来看,当一个系统为封闭的时候,由于负熵无法从外界获得补充,一个子系统发生崩溃时,其崩溃会沿不同的演化路径发生崩溃,且处于不同位置的子系统发生崩溃时对于整个系统崩溃速度的影响是不同的,处于核心位置的子系统一旦受到巨大冲击则会使得系统快速发生崩溃。这说明进行控制时不仅要从外界补充负熵,还应该辨别不同子系统发生崩溃时对整个系统造成的影响,及时将负熵补充到重要的位置上。
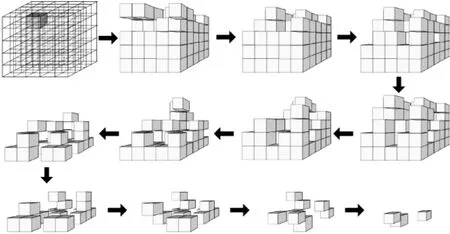
图3 边缘位置的三维元胞自动机系统崩溃模拟
三、公共危机的系统分析
公共事件具有其特殊性,构成一个公共危机事件的子系统之间的熵值如何进行量化和确定?这就需要对复杂系统的脆性风险结构进行剖析[10]。首先复杂系统可以分为两个主要组成部分,即内部机制和外部机制,其中内部机制也可以称为复杂系统内部构成即子系统构成整个系统的结构,这是构成脆性的内因。外部机制也可以成为影响复杂系统子系统的一系列事件和因子的组合[11]。复杂系统各个层次之间,即子系统、脆性事件、脆性因子之间均存在着相互作用和相互联系的可能。
完整的系统可以由若干个子系统组成,每一个子系统往下可以划分为若干个可能导致子系统发生崩溃的脆性事件的集合。因为脆性事件具有潜在性、隐匿性、突发性、复杂性等特点,在实际操作中很难对某一脆性事件进行定量分析,直接利用脆性事件对系统风险进行预测或预警几乎不可能。为此,一般的做法是对脆性事件继续分析,将导致其具有脆性特征的基本脆性因子分离出来。脆性因子是导致脆性事件构成威胁的基本要素,不同脆性因子的组合可能会构成不同的脆性事件,相对于脆性事件本身而言,脆性因子特征相对稳定。因为不同因子所起到的作用也不同,所以在对脆性因子进行定性时要根据其作用的大小界定主次,在定量分析时应赋予不同权重。整个系统脆性程度可以由其子系统或者进而由脆性事件及脆性因子决定,对于具体的脆性因子,可以对其脆性级别进行分类,但是对系统的整体脆性环境应该怎样进行描述呢?利用有效的方法对各个脆性因子的脆弱性进行统一划分,用以描述出整个复杂系统的脆性环境是亟待解决的重要问题。通常来说可以利用神经网络对历史数据进行训练处理,从而得到系统整体脆性环境与各个脆性因子脆性之间的函数关系,从而利用脆性因子的脆性得分来预测整个系统的脆性环境。但是神经网络对于数据量要求较大且精度较低,因此本研究采用基于数据挖掘技术的支持向量机作为分类预测的方法进行分析和研究。
四、基于支持向量机的脆性熵预测
1.支持向量机的基本原理
SVM算法是由Cortes和Vapnik[12]于1995年在统计学理论基础上提出的一种新机器学习方法,它遵循结构风险最小化原则且可以对基于小样本高维度非线性系统实现精确拟合,具有较好的泛化能力。SVM的基本思想是把输入向量通过非线性映射函数φ(x)将数据xi映射到高纬度特征空间F,并在F上进行线性回归。SVM在高维特征空间中的回归函数为

上式中φ(x)为Rm空间到F空间的非线性映射函数,x∈Rm,w为权向量,b为偏置向量。根据机构风险最小化原则,可以转化为如下最小化的线性风险泛函

式中:‖w‖2反映了模型的复杂程度,其值越小则置信风险越小;ε为不敏感损失系数;ζi,ζ*i为松弛变量;C为惩罚变量;n为样本的容量。式(4)是一个标准的约束优化问题,可运用拉格朗日函数法对其求解[13]。由此可以得到SVM回归函数

式(5)中α和α*表示拉格朗日乘子。K(xi,xj)为高维空间内积运算核函数,可表示为K(xi,xj)= φ(xi)φ(xj)。鉴于径向基核函数较其他核函数具有参数少,性能好的特点,所以本研究采用径向基核函数作为SVM的核函数[14],其定义如下
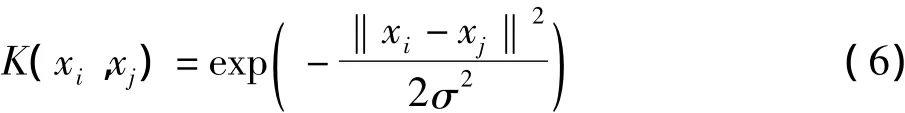
式(6)中σ为径向基核函数的宽度参数。
2.脆性因子的分类等级
脆性因子对系统的作用主要体现在具有使系统突然崩溃的能力上,影响脆性因子的作用能力的因素主要有2个:脆性敏感度和恢复力。据此,系统之间的脆性敏感度可以划分为5级:1级为微度脆弱;2级为轻度脆弱;3级为中度脆弱;4级为深度脆弱;5级为极度脆弱。具体对于某一脆性事件的发生具有复杂性和隐匿性,因此想要通过直接对其脆性进行计算并不可能,比较恰当的做法是先利用德尔菲法对其进行等级分类。基本做法是利用匿名的方式获得专家的意见,将意见统一汇总后取收敛值[15]。为了验证方法的有效性,本研究选取12个交通道路危机作为研究样本,每个危机大致划分为4个脆性事件,分别为脆性事件Y1,Y2,Y3,Y4,每个脆性事件又可以分为若干个脆性因子,取前10个样本作为训练样本输入支持向量机,获得分类器后对后两组样本进行预测验证。各个危机事件的脆性熵指标数据和测评等级情况如表1所示,限于篇幅,本文只给出部分数据情况。
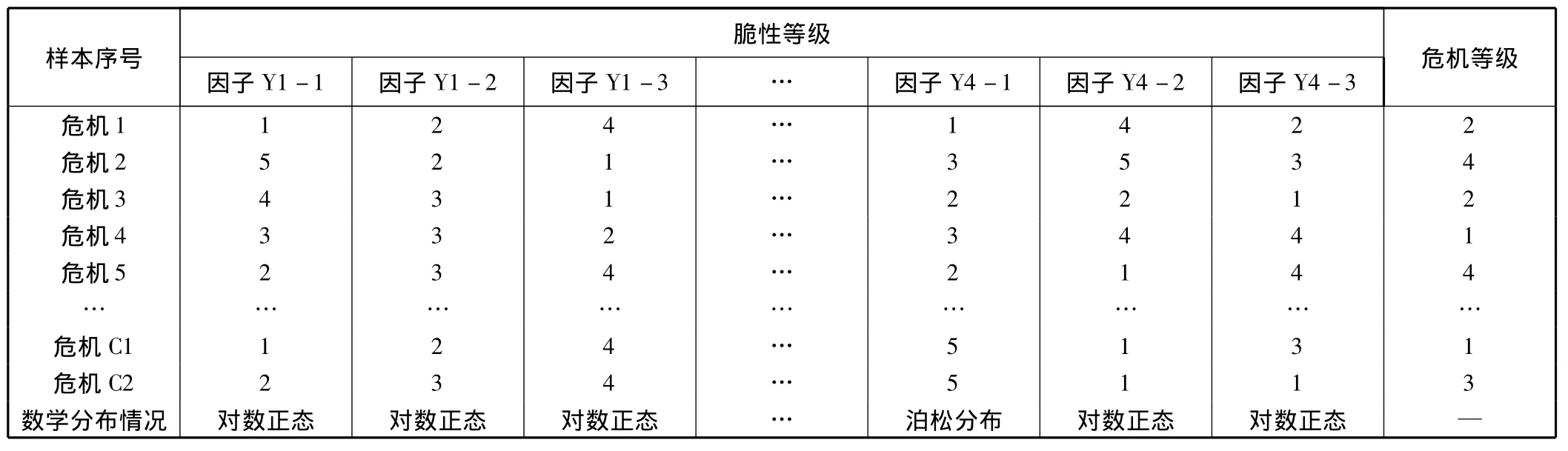
表1 脆性熵的指标数据与测评等级
本文运用Matlab7.0语言编程实现支持向量机的训练与预测算法。首先运用一部分样本进行训练,对最后两个危机C1和C2进行预测,最终的预测结果如图4所示。
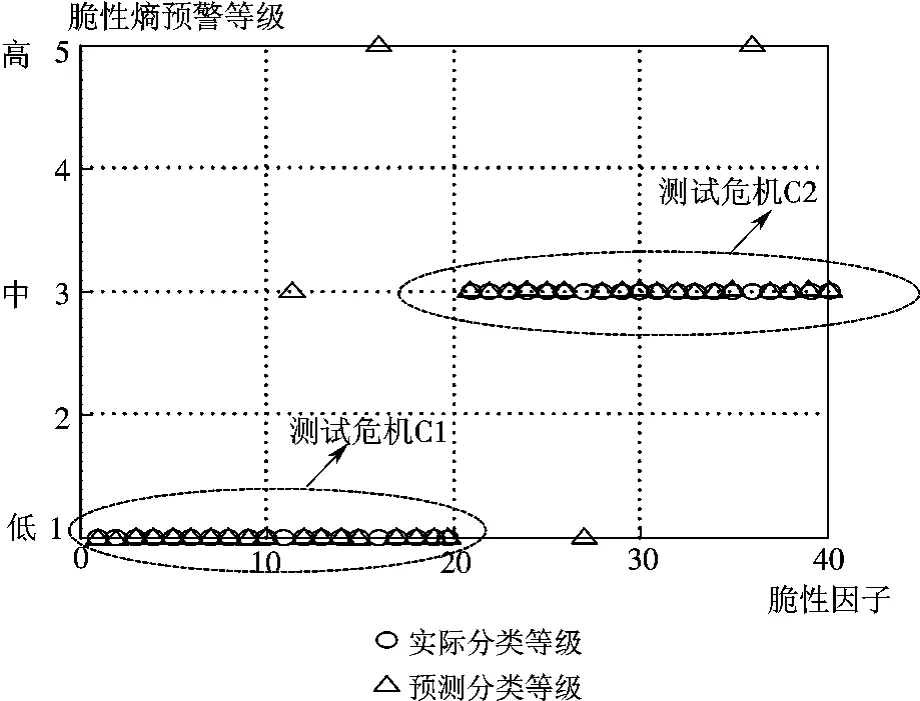
从图4可以看出,当支持向量机达到参数最优时,通过对前10个危机事件的训练得到支持向量机的分类器,用于对后两个测试样本进行测试。可以发现,支持向量机的预测模型可以完全正确地预测测试样本的危机等级,这表明支持向量机能够有效运用于社会安全预警中。在对脆性因子的分类中,支持向量机的分类共有3个判断失误,如图中三角形,但是不会影响总体等级的判断,随着训练样本的增加,模型的精度也会得到提高,这一问题可以得到改善。
六、结语
本研究基于复杂系统视角,探讨了公共事件的冲击对于社会稳定系统可能造成的影响,对复杂系统之间的崩溃模式进行了机理说明,并在此基础上运用元胞自动机进行了仿真模拟。在以上研究基础上提出了运用数据挖掘的方法——支持向量机模型对公共危机事件可能发生崩溃的脆性等级进行了预警。通过实验发现,本研究所提出的方法能够有效对危机事件可能产生的影响进行预警。
值得注意的是,造成复杂系统发生崩溃的“熵”还是一个物理学的概念。本研究认为,社会稳定系统发生崩溃机理与物理学中“熵”导致的崩溃机理是一致的,不同的是在社会系统之间的“熵”包含的内容要复杂得多,究竟是什么样的内容和作用共同构成了“熵”,如何利用“熵”理论对危机事件造成的社会稳定系统崩溃进行控制,是作者下一步进行研究的重要方向。
参考文献:
[1]Verhoeven P.Crisis?What crisisi?How European professionals handle crises and crisis communication[J].Public Relations Revies,2013(1):107-109.
[2]Yan Jin.Examining publics’crisis responses according to different shades of anger and sympathy[J].Journal of Public Relations Research,2014(1):79-101.
[3]刘霞.公共危机治理:理论建构与战略重点[J].中国行政管理,2012(3):116-120.
[4]韦琦.复杂系统崩溃的脆性致因研究[J].系统工程,2003,21(4):1-5.
[5]于丽英,蒋宗彩.基于复杂系统观的城市群公共危机形成机制研究[J].系统科学学报,2013(3):62-65.
[6]韦琦,金鸿章,郭健.基于脆性联系熵的复杂系统崩溃致因研究[J].自动化技术与应用,2003,22(4):1-4.
[7]Coombs W T.How publics react to crisis communication efforts:Comparing crisis response reactions across sub-arenas [J].Journal of Communication Management,2014(1): 40-57.
[8]Karcanias N,Ali G H.Sysem of systems and emergence part 1:Principles and framework[C]//Proc.of the 4th International Conference on Emerging Trends in Engineering and Techonology,2011(1):27-32.
[9]Ender T,Leurck R F,Weaver B,et al.System-of-systems analysis of ballistic missile defense architecture effectiveness through surrogate modeling and simulation[J].IEEE Systems Journal,2010,4(2):156-166.
[10]Liu Yi,Ma Yefeng,Deng Qing,et al.Public opinion analysis and crisis response in mass incidents:A case study of a flight delay event in China[J].Web-Age Information Managment,2014(1):77-86.
[11]金鸿章,李琦,吴红梅.基于脆性因子的复杂系统脆性分析[J].哈尔滨工程大学学报,2005,12(12):739-743.
[12]Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer-verlag,1999.
[13]张水波,康飞,李祥飞.基于支持向量机的建设工程项目经理胜任力评价[J].中国软科学,2013(11):83-90.
[14]李祥飞,张再生.基于误差同步预测的SVM金融事件序列方法[J].天津大学学报:自然科学与工程技术版,2014(1):86-94.
[15]田军.基于德尔菲法的专家集成模型研究[J].系统工程理论与实践,2004(1):62-69.
Study on Public Crisis Pre-control Based on the Perspective of Complex System’s Brittleness
Li Xiangfei,Yan Yaojun
(College of Management,Tianjin Polytechnic University,Tianjin 300387,China)
Abstract:Public crisis events have the traits of uncertainty,irregularity of evolution.The complex relationship between different events makes the public crisis events easy to form a chain reaction impact and exerts a huge impact on the social stability.Therefore,how to predict and control the influence of the public crisis has became one of the most important issues in the emergency management study field.Based on the complex system’s brittleness,the social system is regarded as a complex system composed of several subsystems in this paper.Besides,we discuss and simulate the potential collapse mode and evolutionary mechanism caused by public crisis events.Finally,the early warning method is put forward based on support vector machine(SVM).Our research conclusion can provide reference for establishing and perfecting the public crisis warning system.
Keywords:complex system;brittleness;public crisis;pre-control
通讯作者:李祥飞,soar.li@163.com.
作者简介:李祥飞(1986—),男,博士,讲师.
基金项目:国家社会科学基金重点资助项目(13ASH003).
收稿日期:2014-10-03.
中图分类号:C93-05
文献标志码:A
文章编号:1008-4339(2015)02-188-05

