基于主成分分析和Eros 的邻近传播算法在金融数据集中的应用

廖洪一，王 欣

(中国民用航空飞行学院计算机学院，四川 广汉 618300)

0 引言

时间序列(Time Series)是和时间变化相关联的数据，在每个时间点都会有与之相对应的一系列观察值。在现代社会，时间序列广泛地存在于各个领域中，如生物信息的RNA 序列、心电图变化、商场销售额和传感器网络收到的数据等。时间序列数据的挖掘是通过对这些数据观察值的分析归类来提取决策者关心的有效信息［1］。相较于一般静态数据而言，时间序列数据呈现了待分析数据集一段时期内的状态，并且数据集内的数据之间存在时间上的联系。金融时间序列是在人类的金融活动中伴随产生的，由于人类活动具有周期性，因此在一定历史时期内金融时间序列总是会与历史数据表现出惊人的相似性，如何合理地利用这些历史数据，并通过以往的金融时间序列进行分析，挖掘出潜在的、有价值的信息是学者们急需解决的问题。

目前使用得比较广泛的金融时间序列聚类方法有k-均值聚类算法［2］、基于RBF 神经网络算法、基于ICA 的时间序列聚类方法［3］、基于AP-NN 的混合模型聚类算法、基于谱聚类的时间序列聚类算法［4］和基于蚁群的时间序列算法［5］等，由于时间序列数据的多维性和高噪声性，传统的聚类算法往往在聚类过程中会增大时间和空间上的复杂度。本文提出一种基于扩展范式(Extended Frobenius Norm，Eros)的近邻传播聚类算法(Affinity Propagation，AP)，并结合主成分分析方法(Principal Component Analysis，PCA)先对多维多变量时间序列数据进行降维处理，再选取多变量时间序列数据的主成分进行聚类，可以有效地提高聚类的准确性、稳定性以及鲁棒性。

1 基于Eros 的近邻传播聚类算法

1.1 近邻传播算法

聚类分析是建立一个分类模型，首先通过特征的形式来表示数据集中的数据，再按照特征的相似性来进行分类的过程，是人工智能和机器学习的一个重要研究领域［6］。聚类分析使得同一个类中的数据相似性最大，不同类中的数据相似性最小。而时间序列聚类是将时间序列数据集中的数据分组成多个类的过程，是时间序列数据分析中最主要的任务之一。现代研究通过不同的距离和聚类方法的选择，可以得到令人满意的时间序列分类结果。

近邻传播聚类算法［7］是由Frey 等人在2007 年提出的一种新型聚类算法，该算法把样本集中所有数据点都当作潜在的聚类中心，然后通过各个数据点之间的实时信息传递来迭代竞争从而发现聚类，与传统的聚类算法相比，该算法不需要事先确定聚类的个数，更加快速有效。

对于有N 个样本的样本空间X={x1，x2，…，xN}，每一个样本点xi有k 个影响因素，任意2 个样本点xi和xj之间的相似度度量sij选取Eros 距离作为计算方法，数据点之间的Eros 距离越小说明数据点的相似性越大。

根据sij构造相似性矩阵:

矩阵对角线上的元素p 为偏向参数，表示在迭代过程中各个样本点成为聚类中心的可能性大小，不同的p 会影响聚类中心的数目从而产生不同的聚类结果，一般来说，p 值越大，在聚类中心迭代过程中样本点的竞争就会越大。

在近邻传播聚类算法的计算过程中，选择通过矩阵形式的吸引度R 和归属度A 来传递消息。其中吸引度表示样本点作为聚类中心的可能性大小，归属度表示样本点选择对应样本点为聚类中心的可能性大小。数据集的所有样本点通过算法迭代计算所有样本点的吸引度和归属度，直到迭代满足终止条件产生聚类中心，并且所有的样本点都找到对应的聚类中心为止。吸引度和归属度的迭代计算公式为:

更新公式为:

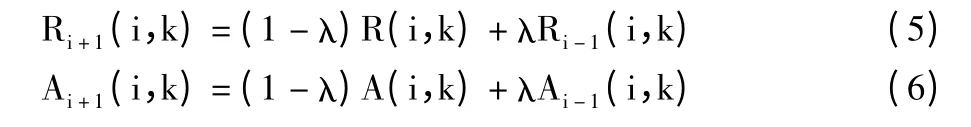
其中，λ(0 ＜λ ＜1，一般设置为0.9)为阻尼系数，用来控制迭代过程中的收敛，不同的阻尼系数迭代过程的收敛和振荡过程不同。

近邻传播聚类算法的计算过程可描述如下:

1)初始化:求解相似度矩阵S，设置参考度p 值，令R0(i，k)=0，A0(i，k)=0。

2)更新吸引度矩阵R 和归属度矩阵A，每更新一次迭代次数加1，直至达到终止条件。

3)判断聚类结果是否达到要求，否则重新设置p值，再重复步骤1)，2)，直到输出的聚类结果满足要求。

1.2 矩阵的Frobenius 范数

设矩阵A 为p×n 的矩阵，并且A=［a1，a2，…，an］，则矩阵A 的F-范数的平方公式如下:

其中tr(A)表示矩阵A 的迹，〈xi，xj〉表示向量xi与向量xj的内积。

设矩阵A 和矩阵B 都是n ×n 的矩阵，并且A=［a1，a2，…，an］，B=［b1，b2，…，bn］，则A -B 的F-范数的计算公式为:

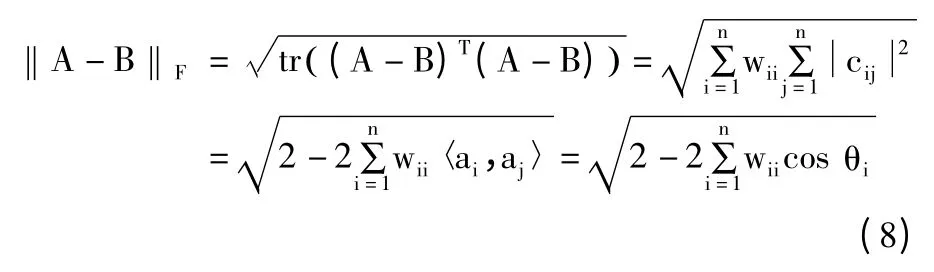
其中，θi是向量ai和向量bi的夹角，W=［wij］是对角半正定矩阵，并且wij=0(i≠j)，=1 且wii≥0。

1.3 矩阵的扩展范式

设A 是pA×n 矩阵，B 是pB×n 矩阵，分别对其协方差矩阵进行奇异值分解，可以得到矩阵A、B的右特征值矩阵VA=[a1，a2，…，an]和 VB=[b1，b2，…，bn]，其中ai，bi是长度为n 的正交向量，则可以将A 和B 的Eros［8］定义为:

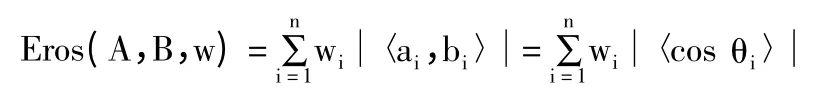
其中，w 是特征值的权重向量，Eros 的变化从0 到1，即相似度在0 时最小，在1 时最大。A 和B 之间的Eros 距离定义为:

至此，2 个纵向数据之间的相似度就可以通过包含主元以及相关特征值的右特征向量来度量。假设式子:Eros(A，B，w)＞Eros(B，C，w)成立，这意味着成立［9］。因此

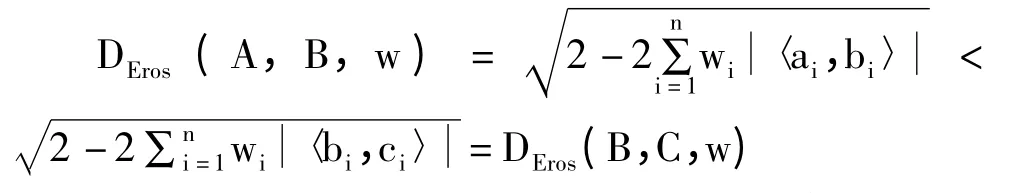
这表明，DEros也相对保留了Eros 的距离，即DEros也表现出Eros 的相似性。

2 主成分分析法优化的近邻传播算法模型

由于多元时间序列的数据集庞大，并且当数据信息冗余时会导致近邻传播聚类算法的计算时间过长。因此如果在多元时间序列中查找出与原序列相似等价的子序列，并确定其相似度就可以对多元时间序列进行降维，以此来降低计算难度，提高聚类的质量。也就是说，将Eros 距离的相似性度量用于去掉冗长信息构造出来的方阵，将会得到更好的效果。

主成分分析方法是通过去掉次要的基本因素，用较少的具有代表性的基本因素表示原始数据的一种多元统计分析方法［10］。它通过将数据集投影到特征空间，再根据数据集在各个特征方向的方差大小排序，再去掉方差较小的特征方向，其实质是数据在多因素影响的情况下如何使用较少的指标表示，或者给多个影响因素进行重要程度的排序。主成分分析方法理论简单，实践性强，结果客观有效，因此是金融、经济、社会科学等领域被使用最为广泛的评价排序方法之一［11］。

传统的主成分分析方法通过搜索较少的几个具有代表性的影响因素来实现对各个样本向量的降维［12］。现使用主成分分析方法对基于Eros 的近邻传播聚类算法进行优化，步骤如下:

1)原始数据集中的样本点向量e1，e2，…，e300都是由6 个随机变量组成，则原始数据集X 可以用一个300 ×6 维的矩阵表示。

2)对矩阵中元素作标准化处理:yij=，其中xij表示第i 个样本点的第j 个影响因素，xj表示第j 个影响因素的样本均值，Sij表示表示第j 个影响因素的样本标准差。得到标准化矩阵:

3)求解标准化矩阵的相关矩阵R 的特征值λ 以及特征向量u，并令λ1≥λ2≥λ3≥…≥λ6≥0。

4)确定p(p≤6)个变量主成分，在实际应用中，一般只找到前p0个主成分即可，其中前p0个主成分方差之和在所有方差中占有较大的比例，并且p0≪p。按照主成分方差λj占所有方差的比例求权系数，j=1，2，…，6。

5)根据主成分的方差贡献率计算样本综合评价值Z=(Z1，Z2，…，Zn)T［13］，其中Z=，由Zi(i=1，2，…，n)值的大小来对样本进行评价排队。

3 实验与分析

3.1 实验数据选取

为了验证算法在金融数据领域的有效性，选取通信达金融数据库系统中300 只股票的相关交易数据进行仿真实验，共覆盖5 个行业，构成原始数据集。只列举前12 只股票分别是:1)古井贡酒;2)国电电力;3)中航飞机;4)潍柴动力;5)中航动控;6)燕京啤酒;7)华能国际;8)华电国际;9)航天科技;10)一汽轿车;11)泸州老窖;12)海马汽车。选取2013 年1 月30 日到2014 年11 月4 日时间跨度为420 个交易日的数据，每只股票的交易情况用每日上证指数的开盘指数最高值、指数最低值、收盘指数、当日交易量、当日交易额、当日开盘指数6 个变量的时间序列来描述［14］。聚类算法通过工具软件Matlab7.1 实现，根据先验知识调节偏向参数的p 值，并在累积贡献率达到95%时确定主元数。

3.2 算法对比实验

为验证基于Eros 的近邻传播聚类算法的有效性，现选取K 均值和凝聚层次2 种同样基于距离的聚类算法作为对比实验。其中K 均值聚类是一种可以把数据集自动划分为K 类的聚类方法，也是当下应用最为广泛的一种聚类方法。凝聚层次聚类［15］则是通过自下而上的方式，通过合成子簇从而达到最终聚类结果。本文将从聚类的准确率和聚类质量2 方面来比较3 种聚类算法的优劣。

3.3 聚类结果评价

为了对聚类结果做出评价，现引入评价指标ASW(Average Silhouette Width)、F-Measure 和熵。

Kaufman 和Rousseeuw 在1990 年提出一种可以对聚类结果进行评价的验证统计量ASW:对于类中的一个对象i，i 的ASW［16］定义为:

F-Measure 是基于准确率和召回率的的一个综合评价。对于任何一个预定类，寻找聚类结果中与之最相似的簇，并根据这个簇计算该类的准确率(precision(i，j)=)，召回率(recall(i，j)=)以及FMeasure。定义类i，j之间的F值为F(i，j)=。至此，整体聚类结果的F 值可以通过加权获得:F=max {F(i，j)}，F值越大说明聚类的准确率越高。

熵用来衡量聚类结果的纯度，熵的值越小说明聚类结果的纯度越大，聚类的效果越好。现将聚类结果的整体熵值定义为:

3.4 实验结果

将股票原始数据集中的数据进行归一化处理后引入主成分分析法模型，计算主元累积率，结果如表1 所示。

表1 列举前12 只股票主元累积贡献率

由表1 可以看出当主成分z=3 时，主元的累积贡献率已经达到95%［17］，包含了原始数据集的绝大部分信息，因此选取前3 个主成分代表原始数据，然后分别用基于Eros 的近邻传播聚类(AP)算法和K均值算法、凝聚层次算法进行聚类比较。

图1 3 种聚类算法的ASW 值

从图1 可以看出基于Eros 的近邻传播聚类算法的ASW 在聚类数目为5 时出现了一个明显的峰值，达到最大值。K 均值算法的ASW 随着聚类数目的增加而缓慢增大，在K=5 时取得最大值，然后ASW 值减小。凝聚层次算法的ASW 先增加后减小K=4 处取得最大值。

图2 3 种聚类算法的F 值

3 种聚类算法在数据集上的F 值如图2 所示。从图中可以看出改进的近邻传播算法结合了主成分分析方法，在准确率几乎不受影响的情况下，提高了召回率，使得该方法的F 值明显大于K 均值算法和凝聚层次算法。

表2 数据集的聚类结果熵值

改进的AP 算法取得了较低的熵值，而K 均值算法和凝聚层次算法的熵值较高。这是因为K 均值算法初始参数的选择会大大影响聚类结果的平衡，凝聚层次算法对于多元时间序列的处理没有优势，而改进的AP 算法聚类纯度高，性能稳定。

综合考虑3 种聚类算法，可以看出与K 均值算法、凝聚层次算法相比，基于Eros 的近邻传播聚类算法的聚类结果具有更高的聚类精度，性能也更加稳定。同时，从聚类结果也可以看出，同一个行业内的股票相似度远远大于不同行业内的股票相似度，同行业之间的股票趋势具有很高的借鉴。

4 结束语

时间序列的聚类问题是时间序列数据挖掘的重要任务之一，针对时间序列的高维性和高噪声性使得一般的聚类算法不能直接应用的问题，本文引入了一种基于主成分分析法和Eros 的近邻传播聚类算法。通过建立多变量的股票时间序列聚类模型，评估该算法在股票时间序列聚类的可行性，并与传统的聚类算法进行对比。近邻传播算法可以自动确定聚类中心和聚类的数目，不需要人工设置初始值，这种通过竞争迭代确定出聚类中心的算法要明显优于传统的给定模型优化的算法。最后通过实验证明了基于Eros的近邻传播算法的有效性，且在聚类精度和算法速度方面要优于传统的聚类算法。

［1］Buyya R，Abramson D，Venugopal S.The grid economy［J］.Proceedings of the IEEE，2005，93(3):698-714.

［2］谢娟英，蒋帅，王春霞，等.一种改进的全局K-均值聚类算法［J］.陕西师范大学学报(自然科学版)，2010，38(2):18-22.

［3］郭崇慧，贾宏峰，张娜.基于ICA 的时间序列聚类方法及其在股票数据分析中的应用［J］.运筹与管理，2008，17(5):120-124.

［4］Maharaj E A，D'Urso P.A coherence-based approach for the pattern recognition of time series［J］.Physica A:Statistical Mechanics and its Applications，2010，389(17):3516-3537.

［5］Caiado J，Crato N，Peñad D.A periodogram-based metric for time series classification［J］.Computational Statist ＆Data Analysis，2006，50(10):2668-2684.

［6］王骏，王士同，邓赵红.聚类分析研究中的若干问题［J］.控制与决策，2012，27(3):321-328.

［7］Frey B J，Dueck D.Clustering by passing messages between data points［J］.Science，2007，315(5814):972-976.

［8］Sambasivam S，Theodosopoulos N.Advanced data clustering methods of mining Web documents［J］.Issues in Informing Science and Information Technology，2006(3):563-579.

［9］Bohm C，Berchtold S，Keim D A.Searching in high-dimensional spaces-index structures for improving the performance of multimedia databases［J］.ACM Computing Surveys，2001，33(3):322-373.

［10］Fang S H，Lin T N.Principal component localization in indoor WLAN environments［J］.IEEE Transactions on Mobile Computing，2012，11(1):100-110.

［11］王德青，朱建平，谢邦昌.主成分聚类分析有效性的思考［J］.统计研究，2012，29(11)84-87.

［12］Climescu-Hauliea A.How to choose the number of clusters:The cramer multiplicity solution［C］// Advances in Data Analysis.2007:15-22.

［13］廖东，杜瑞卿，王骁力.变量线性相关对主成分方差贡献率的影响［J］.河南师范大学学报(自然科学版)，2010，38(6):23-26.

［14］高玉明，张仁津.基于改进QPSO 算法优化SVR 的上证指数预测［J］.计算机仿真，2013，30(12):208-213.

［15］李春忠，徐忠本，乔琛.带信息反馈的凝聚层次聚类算法［J］.中国科学:信息科学，2012，42(6):730-742.

［16］Kaufman L，Rousseeuw P J.Finding Groups in Data:An Introduction to Cluster Analysis［M］.John Wiley and Sons，1990.

［17］杜敏.基于主成分分析法的环境质量综合指数研究［D］.成都:四川大学，2006.