航空发动机需求预测

郭 峰，白 松，周 斌，王 嫣，李永涛

(1.海军航空工程学院青岛校区，山东 青岛 266041;2.海装航空技术保障部，北京 100071;3.91440 部队，河南 洛阳 471023)

0 引言

航空发动机是价格高、供应量大的装备。为了保证飞行训练和作战任务的完成，航空发动机一般是不允许缺货的。为了满足部队的需要，每隔一定周期向生产单位订购一批发动机。订购的数量少了，满足不了部队训练和作战任务的完成;发动机储存多了，在一定时间内用不了，又会造成积压，增大仓库的占用面积和保管费用，造成库存中变质、过期及再次油封等损失［1-6］。

随着技术的进步，新产品的出现，为了减少上述不必要的费用和损耗，库存量愈小愈好，可是库存量太小又可能造成发动机短缺，影响飞行训练和作战任务的完成。

在美国为了提高管理经济效益，采用的是强化供应的办法，一般基层级仓库不存放发动机，只有基地级仓库才贮存。每台发动机安装在哪架飞机上，每天使用的时间及剩余工作时间，都存入计算机中，基地级航材人员随时掌握这些数据，当发动机到寿命后，立即向基层级供应发动机进行更换，保证了飞行训练和作战任务的完成，又节省了航空发动机的库存量，节省了大量的资金［7-8］。

我国在航空发动机需求预测方面有一定的研究。解江等在《基于遗传算法的发动机需求量组合预测方法》中利用遗传算法优化滤波预测、神经网络、灰色预测等4 种预测方法的组合权重，实现了发动机需求的组合预测［9］。航空发动机需求预测的前提就是掌握其消耗规律，但是，该文献预测时只是利用飞行时间和送修台数进行时间序列预测，而对航空发动机的需求规律以及所采用预测方法的适用性没有进行深入地分析。毛海涛等在《航空发动机备份数量需求预测模型的研究》中对影响航空发动机周转备份数量的各主要因素进行了研究分析，提出了发动机正常备份数量、发动机初始备份数量、飞机全寿命周期发动机订货数量和发动机订货数量配齐时间等模型，对合理、经济的订购、备份航空发动机有一定的指导作用［10］。该文献对航空发动机需求规律的分析比较合理，但所采用的理论与方法比较简单，预测模型与需求规律的符合程度有所欠缺，无法确保达到较高的预测精度。

本文从分析导致航空发动机需求的不同因素出发研究其需求规律，然后选择合适的理论与方法对其需求进行预测。

1 需求预测模型

准确预测航空发动机年需求量，是提高保障质量，进行科学管理的重要手段。航材系统为了保证订货、运输和分配的优化，都是以单位的需要作为依据。如果需要计算不准确，多了则造成浪费，少了则影响部队训练和作战任务的完成，因此，在计算航空发动机的需求量时，必须要有科学的依据和先进的计算方法。

1.1 航空发动机需求分析

航空发动机的需求主要是2 种原因导致的，一是使用时间达到规定寿命导致的需求;二是未到寿而提前发生随机故障导致的需求。

规定寿命是指生产(或翻修)工厂所规定的使用时间，写在发动机履历本上。发动机使用只要达到工厂(或翻修厂)规定的使用时间，就被认为发动机已没有寿命，一般就不允装在飞机和航空发动机上继续使用了。发动机装机使用所规定的寿命指标包括使用日历(单位为年)和使用时间(单位为小时)，这2种寿命指标哪一个先达到都表示该发动机到寿。

未到寿而提前发生随机故障，是指发动机在使用中因随机因素的影响，发动机未达到工厂(翻修厂)规定的寿命而提前损坏，外场不能修复。导致随机故障的因素包括生产(或翻修厂)工厂的质量问题，使用中人为不可预防的因素。例如，飞行时飞机被鸟群打坏发动机等，维护人员维护不当造成发动机更换等。由于发动机的修理周期较长，基本没有一年中送修2 次的情况，因此，发动机修复后的再周转对每年的需求基本没有影响。

因此，在计算航空发动机需求量时，应主要考虑2 个方面，即发动机达到规定寿命导致的需求和随机故障导致的需求［11］。由于到寿导致的需求是可以准确预测的确定性需求，随机故障导致的需求是无法完全准确预测的不确定性需求，所以，本文将根据这2个特点对航空发动机的需求进行建模预测。另外，由于发动机不能无限次修理，达到规定的修理次数后就必须报废，因此还要考虑报废对实际需求的影响。

1.2 航空发动机年需求预测模型

航空发动机年需求预测模型为:

其中，S 为发动机年需求量，SA为发动机到达规定寿命的年需求量，SE为发动机发生随机故障导致的年需求量，ρ 为发动机报废率。

1.SA的计算方法。

设某机型全年单机计划飞行小时为T，飞机架数为a，每架飞机上安装的发动机台数为b，第i 台装机发动机规定寿命为t0i、剩余寿命为ti，i=1，2，…，ab，则SA为:

2.SE的计算。

为了使因随机故障而提前更换的发动机数量计算比较符合实际，航材人员要不断地了解情况，掌握规律，想方设法掌握各工厂生产发动机(或翻修发动机)的质量情况，部队人员的维修技术水平，各种可能产生对航空发动机使用寿命的影响，掌握整台发动机及其发动机各个部件发生故障的统计规律，找出发动机提前损坏的概率，或者找出各个备件如主燃油泵、加力燃油泵、滑油附件、燃油滑油附件等损坏的概率，就能求出航空发动机因随机故障导致的年需求量［12-13］。

因随机故障导致的发动机年需求量SE为:

其中，fA为发动机提前更换的频率，即不可靠度，它可以通过以下2 种方法来计算。

1)根据整台发动机的损坏频率计算fA。

设某单位在某一时间段内装机使用的发动机数量，因随机因素的影响更换发动机台数为An，则发动机提前更换的频率近似为:

根据贝努利定律，当n 取无穷大时，fA可以认为是发动机提前损坏的频率。对于发动机备件，就是统计出它提前更换的频率，其计算方法和整台发动机相同。

2)根据发动机的部件不可靠度计算fA。

部件损坏是通过大量实验而得到主要部件的不可靠度来反映出来的。设发动机的可靠度为R，部件的可靠度为Ri(i=A，B，C，…)，R=RA·RB·RC…，则不可靠度为:

3.ρ 的计算方法。

设m 为消耗发动机的总报废量，M 为消耗发动机的总使用量，则ρ 为:

2 算例分析

已知某单位使用某型发动机2008 年至2012 年共使用发动机120 台，因随即故障提前更换的数量是3 台。航空兵部队每年年单机计划飞行小时为120小时，飞机总架数为20，每架飞机上安装的发动机台数为1，装机发动机剩余寿命为分别为ti=520、132、610、110、89、326、357、650、78、53、105、220、286、186、550、662、481、46、220、360，i=1，2，…，20，前10 台规定寿命均为900 小时，其余发动机规定寿命为600 小时。该发动机的报废率为0.05，2013 年的消耗量为6 台，其中，到寿更换了5 台，因故障提前更换1 台。

另外，已知该发动机主要机件使用可靠度为:

1)压气机可靠度R=0.998;

2)尾喷管可靠度R=0.999;

3)涡轮装置可靠度R=0.996;

4)燃烧室可靠度R=0.995;

5)其余部件可靠度R=1。

下面利用上述方法对该发动机2013 年的需求进行预测，并通过与实际消耗量进行比较，来分析本文所述方法的准确性。

Step1计算SA。

根据式(2)，计算发动机到达使用寿命的年需求量，即:

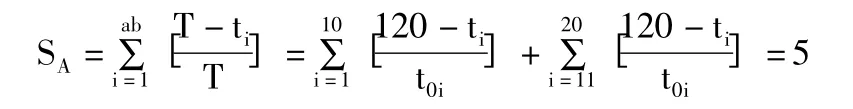
Step2计算SE。

1)根据整台发动机的损坏频率计算fA。

根据式(4)计算fA:

2)根据发动机的部件不可靠度计算fA。

根据式(5)计算fA:

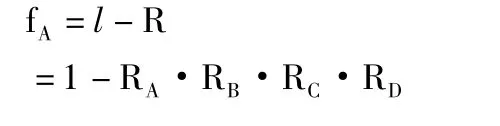
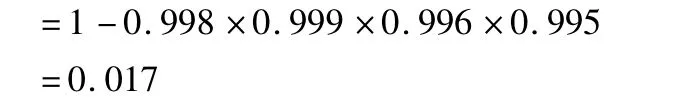
3)根据式(3)计算SE。

Step3计算S。

根据式(1)，计算发动机2013 年的需求量，即:

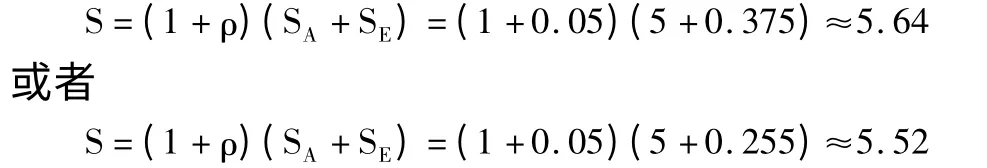
通过整台发动机的损坏频率和发动机的部件不可靠度计算的2 种方法，计算得出的需求量分别约为5.64 台或5.52 台，所以其预测结果基本相同，将其向上取整即可得该发动机2013 年的需求约为6 台。本文所建立的模型预测的2013 年到寿数和发生随即故障的数量与该年度实际的消耗情况完全一致。

另外，根据算例可以发现，要使整个发动机系统可靠度最优，必须各个备件子系统都最优，若系统的某一个备件的可靠度变小，那么整个系统就无法达到最优［14-19］。例如，一台发动机由5 个主要备件组成，若其中4 个备件可靠度为1，只有一个可靠度0.9，那么整台发动机的可靠度反而为0.9，不可靠度则为0.1，也就是有十分之一的发动机可能发生故障而提前更换或在修理中，因此，只有各个子系统都最优，整台发动机或备件才能达到最优。所以，为了进一步提高航空发动机保障水平，航材保障部门有必要和机务、生产厂等单位协同合作，进一步提高航空发动机及其部附件的可靠度。

3 结束语

本文深入分析了航空发动机的需求规律，将航空发动机的需求分为到寿导致的需求和随机故障导致的需求2 部分，然后分别建模预测。算例表明，本文所建立的航空发动机需求预测模型能够基本反映出航空发动机实际的消耗规律，预测结果与实际消耗情况相符，因此具有较高的准确性和实用性。

本文的研究成果对于确保航材保障人员科学合理地管好、用好航空发动机，进一步提高航材保障效益具有重要意义。但是，航空发动机的保障不能完全依靠定量预测。由于航空发动机故障的随机性导致航空发动机的消耗具有极大的不确定性，所以，航材保障还需要通过管理的手段来应对非正常的需求，如紧急订货、调拨等，这样2 种方式结合起来才能最大限度地提高航空发动机的保障水平，确保战训任务的顺利完成。

［1］马绍民.综合保障工程［M］.北京:国防工业出版社，2002:4-5.

［2］王琨.航材的采购与库存管理［D］.南京:南京航空航天大学，2002.

［3］王文亮，程明.对舰载机保障系统的建立及其特点的思考［J］.教练机，2012(1):60-63.

［4］杨秉喜，李金国，张义芳，等.CJB4355《备件供应规划要求》实施指南［Z］.北京:总装备部技术基础管理中心，2006:46-47，50-51.

［5］陈建华.我国航空公司航材周转件计划与库存管理研究［D］.北京:北京交通大学，2009.

［6］韩维，商兴华，李成，等.舰载机维修保障力量需求研究［J］.海军航空工程学院学报，2010，25(6):670-674.

［7］Craig C Sherbrooke.装备备件最优库存建模:多级技术［M］.贺步杰译.北京:电子工业出版社，2008:10-50.

［8］Kumar U Dinesh.可靠性、维修与后勤保障:寿命周期方法［M］.刘庆华，宋宁哲译.北京:电子工业出版社，2010:177-180.

［9］解江，江洋溢，李学文，等.基于遗传算法的发动机需求量组合预测方法［J］.计算机工程，2006，32(24):245-247.

［10］毛海涛，周圣林，吕日毅.航空发动机备份数量需求模型的研究［J］.航空维修与工程，2009(2):44-46.

［11］郭峰，温德宏，刘军，等.绝对寿控航材需求预测［J］.兵工自动化，2013，32(9):32-36.

［12］杜俊刚，何亚群.美空军精确保障下航材可修件供应指标探讨［J］.徐州空军学院学报，2007(4):87-90.

［13］刘兴堂，吴晓燕.现代系统建模与仿真技术［M］.西安:西北工业大学出版社，2001:166-167.

［14］刘杨，任德奎.基于灰色理论的间断性需求备件预测方法［J］.四川兵工学报，2011，32(4):27-29.

［15］吴清亮，董辉，张政，等.基于神经网络对航材备件需求率的预测分析［J］.兵工自动化，2009，28(1):54-56.

［16］万玉成，何亚群，盛昭瀚.基于灰色系统与神经网络的航材消耗广义加权函数平均组合预测模型研究［J］.系统工程理论与实践，2003，7(7):81-87.

［17］何亚群，谭学峰，金福禄.基于可用度的飞机可修件需求分析［J］.系统工程与电子技术，2004，26(6):848-849.

［18］付兴芳，李继军，李宗植.基于两级供应关系的可修复备件存储策略模型研究［J］.系统工程理论与实践，2004(2):111-115.

［19］刘源，陈云翔，周中良，等.基于可用度和费用要求的航材备件储备量优化［J］.空军工程大学学报(自然科学版)，2009，10(6):15-18.