光电编码器单莫尔条纹测速方法
王亚洲,万秋华 ,杜颖财,李俊峰,卢新然
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033;2.中国科学院大学,北京100049)
1 引言
光电编码器是一种利用光栅莫尔条纹为测量基础的光电角位移传感器[1]。广泛用于工业控制、自动化检测及精密测量等领域[2]。在高精度的现代化控制中,编码器的转速是极其重要的反馈信息,因此精确获取编码器的转速具有重要意义。
编码器传统测速方法主要有定时测角法(M法)、定角测时法(T法)和混合测速法(M/T法)[3]。这些方法是发展最早和应用最为成熟的测速方法。因其数据处理量小,运算简单,实时性好,是目前应用最为广泛的测速方法。但是由于其测速精度及测速稳定性的限制,不能满足速度要求高的系统。随着现代控制理论的发展,研究人员提出了改进的传统算法、滤波法以及拟合法等算法来提高编码器的测速精度。如爱尔兰Naveen等人就提出利用一种自学习算法来提高M/T法的测速精度[4]。韩国Se-Han Lee等人提出一种利用积分器代替微分器求速度和加速度的方法[5]。荷兰 R.J.E.Merry等人通过拟合角度关于时间的高次多项式,用以恢复任意时间点的角度信息,同时对角度关于时间求导,得出编码器的速度[6]。北京交通大学文晓燕等人提出一种中断T法[7]。中国科学院长春光机所科研人员利用非线性跟踪微分器来对编码器输出角度进行跟踪,以达到更好的测速稳定性[8]。中国科学院自动化所的王辉等人提出一种角位移拟合测速法[9]。虽然上述算法都可以提升编码器的测速性能,但是大多数还依赖编码器的输出角度,因此测速算法对编码器的测角误差敏感,不能避免编码测角误差对测度精度的影响。编码器莫尔条纹信号的正交性和等幅性等偏差会大大影响编码器的测角精度[10],继而影响编码器的测速精度。
本文提出的光电编码器单莫尔条纹测速方法可以有效的避免上述误差带来的测速误差,同时利用EMD分解法可以有效的避免莫尔条纹信号直流分量带来的测速误差。本文分析了编码器莫尔条纹的产生原理,推导出莫尔条纹信号关于编码器转速的表达式;研究了希尔伯特-黄变换在瞬时频率提取上的原理和优势;然后将编码器AD采集到的莫尔条纹光电信号通过希尔伯特-黄变换,提取出编码器的速度值。实验结果表明本文研究的测速方法精度高,抗干扰性能强。
2 莫尔条纹光电信号测速模型的建立
莫尔条纹光电信号测速是在编码器运动状态下,用AD转换器直接采样编码器莫尔条纹信号,利用各种算法提取速度信息的过程。该过程的信息来源于编码器测量的原始信号,其运算结果不受编码器细分误差的影响,并节省了角度运算时间。
光电编码器由轴系、光源、码盘、狭缝、光敏元件和处理电路组成,系统结构组成如图1所示[11]。
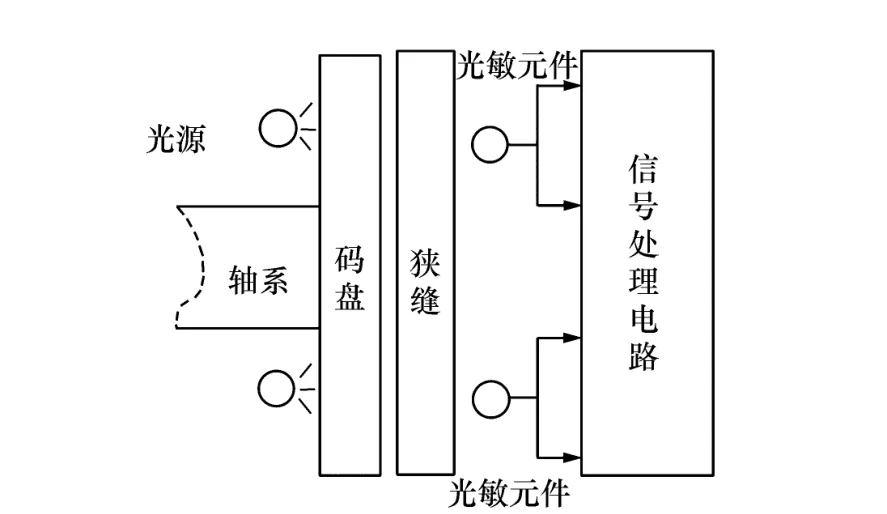
图1 光电编码器组成Fig.1 Composition of the photoelectric encoder
码盘与被测轴连接,光源通过码盘和狭缝射到光敏元件上。当轴系转动时,会带动码盘一起转动,光敏元件可以检测到随着角度变化的光强信号。理想状态下得到的四路光电莫尔条纹信号为:

式(1)中,U0为光电莫尔条纹信号中叠加的直流分量,Ua为信号幅度,x为光栅位移,p为光栅间距。上述信号经过差分运算可以到两路标准的正余弦信号:

通过式(2)可得编码器输出的莫尔条纹光电信号为随光栅位移成正弦变换的信号。
归一化处理后:

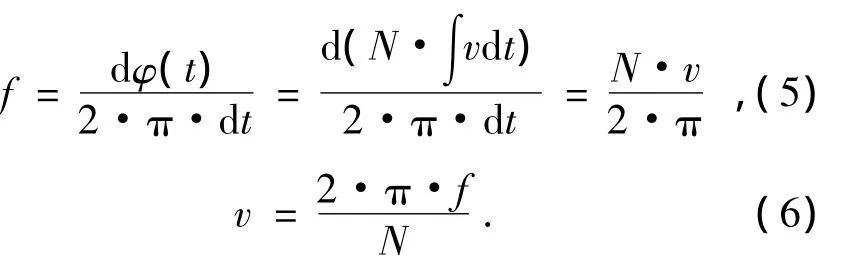
由式(6)可得编码器输出莫尔条纹信号的瞬时频率与编码器的转速成正比。因此只需要利用编码器莫尔条纹光电信号提取出其瞬时频率,就可以求解编码器的瞬时速度。
3 基于希尔伯特-黄变换的单莫尔条纹测速方法
3.1 希尔伯特变换-黄变换原理
希尔伯特-黄变换(HHT)是美籍华人工程师黄鄂于1998年提出的一种新的信号时频分析理论[12]。通过固有模态(IMF)和经验模态筛选法(EMD)的引入可以将信号分解为一系列(有限个)本征函数和残余函数的和。然后对每个本征函数进行希尔伯特变换就可以得到有意义的瞬时频率。
希尔伯特变换[13]对输入序列的各次谐波都能有精确的90°移相,给定一连续周期信号x(t),对于给定的关于时间连续的实信号x(t)的希尔伯特变换定义为:

式中,P.V.表示取柯西主值。
利用上述希尔波特变换的结果构造原实信号的解析信号Z(t):

欲使上式定义的瞬时频率有意义,必须使信号在局部范围内对称于零均值。理想条件下莫尔条纹光电信号正满足这一特点。但由于误差和直流分量的存在,使得莫尔条纹信号并不能完全满足这一条件。基于希尔伯特变换的这一缺点,黄提出了固有模态和EMD分解法来解决。
EMD即经验模态分析法是一种将复杂信号分解成固有模态的分析方法。该方法认为所有信号可以分解成不同频率的本征模态和残余函数的和。其中本征模态函数满足以下两个条件:
(1)在整个数据序列中,极值点和过零点的数目必须相同,或者数量相差为1。
(2)在任意时刻上,由局部极大值和局部极小值定义的上下包络线的平均值为零。
由于莫尔条信号十分类似于标准正余弦信号,满足上述条件,所以可按照以下精简的EMD方法来滤除直流分量的影响。(a)首先找出x(t)所有的极大值点和极小值点,并用三次样条函数分别拟合原函数的上、下包络线;(b)求取上下包络线的平均值,记做m1(t),求取x1(t)=x(t)-m1(t);经过EMD分节后得到的x1(t)信号,在局部范围内排除直流分量对瞬时频率的影响满足希尔伯特变换的要求。
3.2 单莫尔条纹测速方法
通过上述分析可以发现,希尔伯特-黄变换在瞬时频率的提取上具有巨大优势,而编码器的莫尔条纹光电信号正是频率随转速线性变换的信号。因此通过希尔伯特黄变换就可以完成编码器速度的提取。由式(7)可以发现,希尔伯特变换是一个非因果系统,即当前时刻信号的希尔伯特变换需要全时域上的信号幅度,是物理不可实现系统。但是通过希尔伯特变换的公式可以发现,离当前时刻越远的信号对当前时刻信号的希尔伯特变换结果影响就越小。公式可以改写为:

故当T足够大时信号对当前时刻的希尔伯特变换的影响可以忽略不计。在实际测速中取T为测速延时,即测量结果经过T延时后可以得到。公式可以表示为:

经过实际的实验发现,当T时间内转过两个以上莫尔条纹周期时,运算结果的波动会淹没在信号噪声中。即时希尔伯特变换的非因果性带来的影响可以忽略不计。
由于固有模态和EMD分解法的提出,使得在实际的测速中原始莫尔条纹信号既可以来源于式(1)中的原始莫尔条纹信号,也可以来源于式(2)中处理过的光电莫尔条纹信号。具体处理步骤如下:
Step1:将AD采样得到的莫尔条纹信号数据,利用EMD分解法将其分解成一系列的本征模态函数和残余序列;
Step2:根据原始信号的频率特性,选取合适的频率的IMF函数,由于莫尔条纹光电信号基本是标准的正弦,因此只需要选取x1(t)就可以满足希尔伯特变换的要求;
Step3:对选取的IMF分量做希尔伯特变换,并构造其解析序列。根据器解析序列的角度变化率计算编码器莫尔条纹光电信号的瞬时频率;
Step4:结合采样频率和编码器具体参数,计算编码器转速。
与其他测速方法相比,由于本文提出的测速方法不受编码器测角误差的影响,所以具有其他测速方法不具备的精度。由于希尔伯特变换需要全时域信号值的特点,使得算法具有很好的速度稳定性。在实现上述优点的同时牺牲了一定的测速延时和算法复杂度。对比表见表1。

表1 测速性能对比Tab.1 Performance comparison of velocity measurement
4 实验及数据分析
以中国科学院长春光机所某型号21位编码器进行测速实验,采用2K采样频率。为了获得较为平滑的速度,实验选取编码器在0.15 s内的数据值,由于测量时间比较短,而且系统的整体惯量比较大,故认为编码器在被测时间内其转速是均匀的。为了对比本文所述方法的精确度,在采集编码器莫尔条纹的同时,用电脑记录编码器的实时输出角度。并利用最为常用的M法,完成测速。实验装置如图2所示。

图2 单莫尔条纹测速装置Fig.2 Velocity measuring device based on single moire fringe
利用DSP采集到的编码器莫尔条纹信号经过EMD分解后的波形如图3所示。
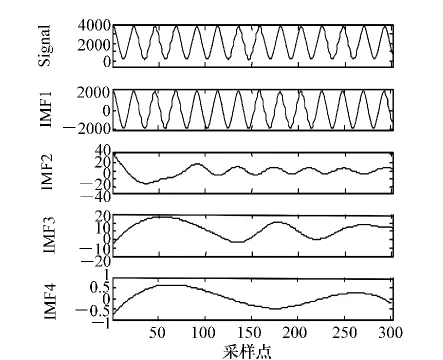
图3 EMD分解结果Fig.3 Results of EMD decomposition
由图可以看出,经过EMD分解后的IMF1与原信号的频率和相位一致,并且去除了直流分量,故可作为希尔伯特变换的数据。
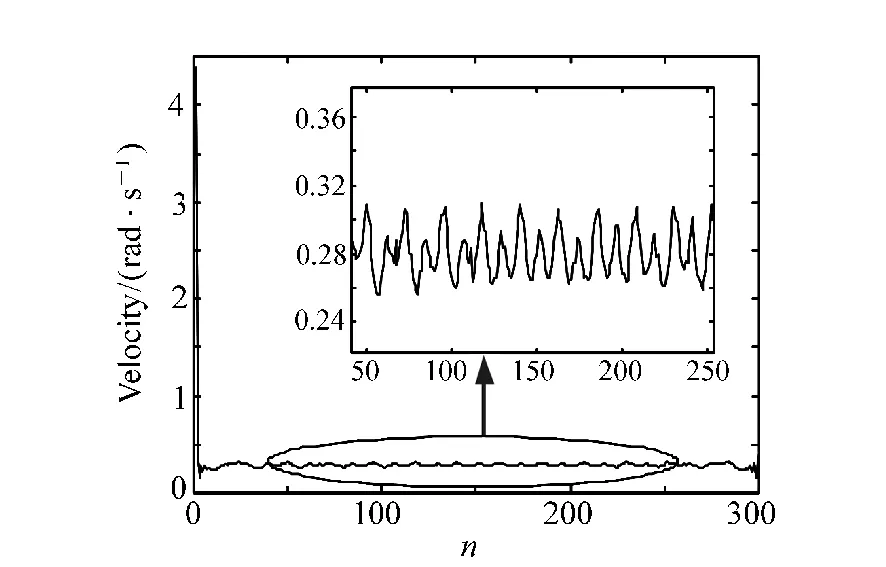
图4 基于正弦信号的测速结果Fig.4 Velocity measuring results based on sine signal
利用希尔伯特-黄变换的测速结果如图4所示。图3测速结果是采用式(2)中的正弦信号,由测速结果可以发现,采用希尔伯特-黄变换所得的测速结果在数据的开始和结束的时候会有较大的波动,这是由于采集时间窗造成的频谱泄露,所以会产生较大的频率冲击。由图可以看出,在取T为0.025 s即测速延时为0.025 s时,信号的断点对频率的测量结果的影响可以忽略。所得测速结果如图3中放大区域所示。不考虑测速延迟的情况下,仅取在0.025~0.125 s,0.1 s内的数据,经过计算可得图3的测速误差标准差为0.013 4 rad/s。
为了对比该方法的测速精确性选取了M法的测速结果作为对照实验。测速结果如图5所示。
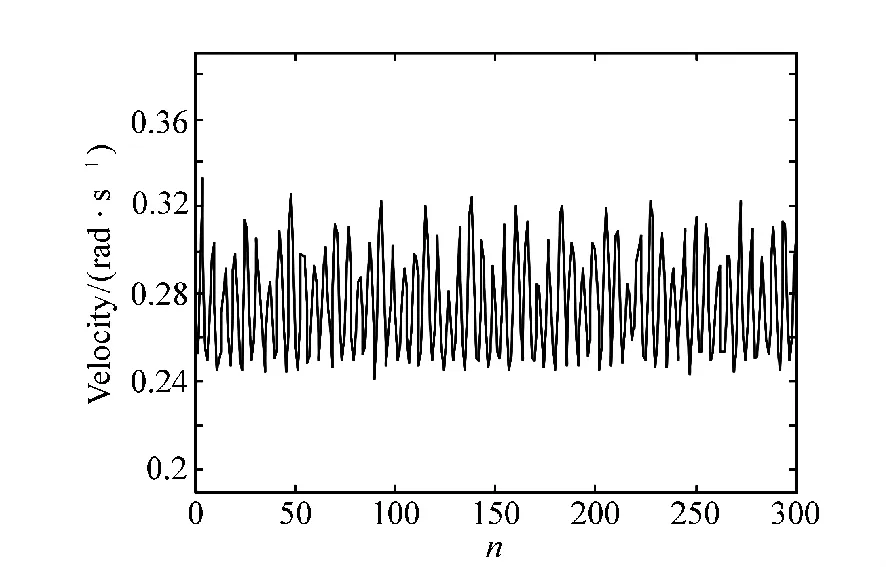
图5 M法测速结果Fig.5 Velocity measuring results of M method with orthogonal correction
由图5测速结果可以发现采用M法测速,基本不存在测速延时,但是其测速稳定性差。为了获得较好的对比效果,同样选取M法测速结果中在0.025~0.125 s,0.1 s内的数据,M法测速误差标准差为0.022 4 rad/s。经过数据对比可以发现基于希尔伯特-黄变换的编码器莫尔条纹测速法,所得测速结果测速稳定性好,抗干扰能力强。
5 结论
本文提出基于希尔伯特-黄变换的光电编码器单莫尔条纹测速方法。利用希尔伯特-黄变换提取编码器莫尔条纹信号的瞬时频率,结合编码器的具体参数可以求取编码器的瞬时速度。直接通过莫尔条纹测速可以避免编码器细分误差带来的测速误差。同时该方法只需要一条莫尔条纹光电信号即可完成测速,避开了正交性偏差的影响。通过对某21位编码器进行测速实验,对比M法测速结果,其测速误差均方差由原来的0.022 4 rad/s降低到0.013 4 rad/s。实验结果表明,本文提出的测速方法测速稳定性高,抗干扰能力强,可用于精度要求较高的测速场合。
[1] 叶盛祥.光电位移精密测量技术[M].成都:四川科学技术出版社,2003,4-7.YE SH X.Accurate Measurement about Photoelectric Shift[M].Chengdu:Sichuan Science and Technology Press,2003.(in Chinese)
[2] 冯英翘,万秋华,王树洁.小型光电编码器长周期误差的修正[J].光学 精密工程,2014,22(9):2491-2497.FENG Y Q,WAB Q H,WANG SH J.Correction of long-period error for small photoelectric encoders[J].Opt.Precision Eng.,22(9):2491-2497.(in Chinese)
[3] 宋刚,秦月霞,张凯,等.基于普通编码器的高精度测速方法[J].上海交通大学学报,2002,36(8):1169-1172.SONG G,QIN Y X,ZHANG K,et al..Approach and realization to improve the measuring accuracy with resolution encoder[J].Shanghai Jiaotong University,2002,36(8):1169-1172.(in Chinese)
[4] NAVEEN K B,RICHARD C K.New learning algorithm for high-quality velocity measurement from low-cost optical encoders[C].IMTC 2008-IEEE Instrumentation and Measurement.Victoria,Vancouver Island,British Columbia,Canada,May 12-15,2008:1908-1913.
[5] SE H L,JAE B S.Accleration estimator for low-velocity and low-acceleration regions based on encoder position data[J].IEEE/ASME Transactions on Mechatronics,2001,1(6):58-64.
[6] MERRY R J E,VAN M J G,MOLENGRAFT D,et al..Velocity and acceleration estimation for optical incremental encoders[J].Mechatronics,2010,20:20-26.
[7] 文晓燕,郑琼林,韦克康,等.增量式编码器测速的典型问题分析及应对策略[J].电工技术学报,2012,27(2):185-189.WEN X Y,ZHENG Q L,WEI K K,et al..Typical issue analysis and corresponding strategy for incremental encoder speed measurement[J].Trans China Electrotechnical Society,2010,27(2):185-189.(in Chinese)
[8] 黄法军,万秋华,杨守旺.莫尔条纹光电信号的非线性跟踪微分测速方法[J].红外与激光工程,2014,43(6):1930-1935.HUANG F J,WAN Q H,YANG SH W.Method of velocity measurement based on Moiré fringe and nonlinear tracking differentiator[J].Infrared and Laser Engineering,2014,43(6):1930-1935.(in Chinese)
[9] 王辉,胡建华,王慎航.增量式光电编码器角位移拟合测速算法[J].仪表技术与传感器,2014(10):99-101.WANG H,HU J H,WANG SH H.Angular position fitting velocity detection of incremental oрtical encoder[J].Instrument Technique and Sensor,2014(10):99-101.(in Chinese)
[10] 王显军.光电轴角编码器细分信号误差及精度分析[J].光学 精密工程,2012,2(20):379-386.WANG X J.Errors and precision analysis of subdivision signal for photoelectric angle encoders[J].Opt.Precision Eng.,2012,2(20):379-386(in Chinese)
[11] 孙莹,万秋华,王树洁.航天级光电编码器的信号处理系统设计[J].光学 精密工程,2010,18(5):1182-1188.SUN Y,WAN Q H,WANG SH J.Design of signal process system for spaceborne photoelectric encoder[J].Opt.Precision Eng.,2010,18(5):1182-1188.(in Chinese)
[12] 苗晟,王威廉,姚绍文.Hilbert-Huang变换发展历程及其应用[J].电子测量与仪器学报,2014,28(8):812-818.MIAO S,WANG W L,YAO SH W.Historic development of HTT and its applications[J].J.Electronic Measurement and Instrumentation,2014,28(8):812-818.(in Chinese)
[13] 高旭,万秋华,李金环,等.光电轴角编码器莫尔条纹误差信号补偿[J].红外与激光工程,2015,44(2):647-653.GAO X,WAN Q H,LI J H,et al..Photoelectric shaft encoder error of moire fringe signal compensation[J].Infrared and Laser Engineering,2015,44(2):647-653.(in Chinese)
[14] 钟佑明.希尔伯特-黄变换局瞬信号分析理论的研究[D].重庆:重庆大学,2002.ZHONG Y M.Research on the local-instantaneous signal analysis theory of the Hilbert-Huang transform[D].Chongqing:Chongqing University,2002.(in Chinese)

