非完整矩阵的分析及其在目标定位中的应用
赵琦,胡泽鹏,汤四龙,万群
(1.吉林省无线电监测站,长春130000;2.电子科技大学电子工程学院,成都611731;3.同方电子科技有限公司,江西九江332007)
【信息科学与控制工程】
非完整矩阵的分析及其在目标定位中的应用
赵琦1,胡泽鹏2,汤四龙3,万群2
(1.吉林省无线电监测站,长春130000;2.电子科技大学电子工程学院,成都611731;3.同方电子科技有限公司,江西九江332007)
在高维空间中认识、分析和处理信号与数据是现代信号与信息处理的重要方法,可以将问题简化为如何确定或优化点、线、面之间的线性关系问题,避免复杂的非线性处理带来的性能分析、工程实现上的问题;但是,在实际应用中经常遇到信号和数据矩阵中的元素出现缺失的情况,增加了子空间分析的难度;通过几个简单的例子,研究了非完整矩阵的子空间方法及其在目标定位中的应用,并给出了性能优化和资源优化的处理方法。
非完整矩阵;子空间分析;目标定位
1 概述
子空间分析方法是现代信号与信息处理的基本方法之一[1],由于在高维空间中可以将非线性参数估计问题转化为线性参数估计问题,非线性信号处理的主要问题也就转化为如何确定或优化点、线、面之间的关系问题,该方法不仅可以用于解决、分析线性信号处理问题,还可以用于解决、分析许多非线性信号处理问题。
以经典的频率估计问题为例子,信号模型为x(t)=asin(ωt+φ),问题是如何利用观测样本x(t),t=1,2,…,T,估计信号角频率ω。从基于时域信号波形的问题描述和处理方式上来看,该问题属于非线性参数估计问题,x(t)是由角频率和初相决定的关于时间的非线性函数,如图1所示。

图1 x(t)时域波形图
但是,从基于高维空间的问题描述和处理方式上来看,该问题属于非线性参数估计问题,如图2所示,所有的三维向量(x(t),x(t+1),x(t+2))都位于一个低维的子空间平面上,换句话说,所有的三维向量(x(t),x(t+1),x(t+2))的3个元素之间都满足一种由角频率ω决定的线性关系。

图2 (x(t),x(t+1),x(t+2))三维立体图
目前,基于完整的信号或数据矩阵的子空间分析方法已经比较成熟,由于信号处理系统的信息采集、传输、存储、计算处理等资源受限,加上实际应用中各种原因导致的信息缺损、不完整,需要进行子空间分析的信号或数据矩阵在实际应用中往往不是完整的,给传统的子空间分析方法带来了较大的挑战[2]。
本文下面先介绍基于非完整信号或数据矩阵的子空间方法,再介绍在目标定位中的应用,最后给出结论。
2 非完整矩阵的子空间方法
以3种天线阵列为例子:8阵元均匀线阵;8阵元的非均匀线阵;由8阵元非均匀线阵通过内插、外推形成的13阵元均匀线阵,如图3所示。这3种天线阵列的波束图如图4所示。
可见,8阵元均匀线阵分辨率较差,8阵元的非均匀线阵旁瓣较高,由8阵元非均匀线阵通过内插、外推形成的13阵元均匀线阵同时克服二者的缺点。
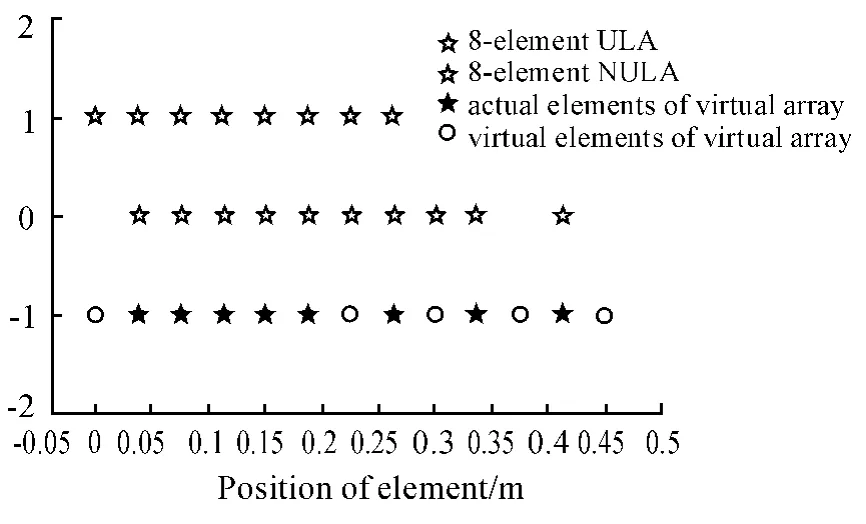
图3 3种天线阵列

图4 3种天线阵列的波束
由8阵元非均匀线阵通过内插、外推形成的13阵元均匀线阵的关键是解决如下非完整矩阵的子空间分析:

其中,

当正黑体标记的元素已知时,上述问题是经典的前后向线性预测问题[3],容易求解,当正黑体标记的元素未知时,就是典型的非完整矩阵的子空间分析问题。
目前,主要通过迭代方法进行近似求解:先确定初始的前后向线性预测系数估计,再利用前后向线性预测系数估计通过求解如下的线性问题确定缺失的元素,然后利用上述前后向线性预测关系由补全的数据矩阵更新前后向线性预测系数估计,最后重复上述过程,直至前后向线性预测方程的拟合误差足够小或收敛到一个稳定的数值:

3 实例分析与应用
子空间分析方法在目标定位中的应用例子很多,包括时频混叠的多信号高分辨率空间谱测向交叉定位、测距(距离差)定位[4-5]、多普勒频率差定位等[6]。但是,当数据矩阵存在缺失的元素时,常规的子空间分析方法不再适用。
以测距定位为例子,在如下的由距离测量确定的测距矩阵中,rk是目标到第k个信号接收站的距离,dmn是第m个信号接收站到第n个信号接收站的距离[7-9](k,m,n=1,2,3):

该测距矩阵又可以写成:

其中(xk,yk)是第k个信号接收站的位置坐标,k=1,2,3,(x0,y0)是目标的未知位置坐标。可见,上述测距矩阵是一个低秩矩阵,有:

其中(s1,s2,s3)是测距矩阵的零特征值对应的特征向量。因此,由测距矩阵的子空间分析即可确定其零特征值对应的特征向量,由此代入上式即可确定目标位置。
考虑到每个距离测量都要消耗信号带宽、信息传输、计算处理、能量等资源,在资源受限、信号受到干扰、信号传播条件被破坏等情况下,测距矩阵中将存在缺失的元素,难以直接利用非完整的测距矩阵快速提取目标位置信息。
常规处理方法是先利用完整的测距矩阵的低秩特性恢复缺失的数据,再采用现有的子空间分析方法进行定位估计[10]。这种方法是在走弯路,实际上可以利用完整的测距矩阵的低秩特性直接确定目标的位置参数,而不需要恢复缺失的数据。当缺失的数据较多时,直接估计参数的方法可以满足实时定位理的要求。
4 结论
信号或数据矩阵的子空间分析为我们在高维空间中认识、分析和处理信号与数据提供了一种重要的工具,当实际应用中遇到信号和数据矩阵中的元素出现缺失的情况时,需要发展非完整矩阵的子空间分析方法,在实现性能优化的同时,满足资源优化的需要。
[1]游鸿,黄建国.子空间投影DOA估计算法分析及合成空间谱[J].航空学报,2008,29(5):1334-1339.
[2]朱翠.具有非完整信息系统的滤波和数据融合算法研究[D].北京:北京理工大学,2014.
[3]史杰,钟雄虎,宋叔飚,等.基于前后向线性预测的时变参数估计方法研究[J].计算机测量与控制,2006,14(11):1515-1518.
[4]Huang J Y,Wan Q,Wang P.Minimum mean square error estimator for mobile location using time-difference-of-arrival measurements[J].IET Radar,Sonar&Navigation,2011,5(2):137-143.
[5]He-Wen Wei,RongPeng,Qun Wan,et al.Multidimensional Scaling Analysis for Passive Moving Target Localization with TDOA and FDOA Measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1677-1688.
[6]肖尚辉,江毅.基于频域子空间的UWB信道时延估计算法研究[J].西南民族大学学报自然科学版,2007,33(3):563-567.
[7]Qin S,Wan Q,Duan L F.Fast and efficient multidimensional scaling algorithm for mobile positioning[J].IET Signal Processing,2012,6(9):857-861.
[8]Qin S,Wan Q,Chen Z X.A Fast Multidimensional Scaling Analysis for Mobile Positioning[J].IET Signal Processing,2011,5(1):81-84.
[9]Qin S Q.Wan Z X.Fast subspace approach for mobile positioning with time-of-arrival measurements[J].IET Communications,2011,5(14):2035-2039.
[10]Fei Wen,Qun Wan,Hewen Wei,et al.Improved MUSIC Algorithm for Multiple Noncoherent Subarrays[J].IEEE Signal Processing Letters,2014,21(5):527-530.
(责任编辑杨继森)
Incomplete Matrix Analysis and Its Application to Target Localization
ZHAO Qi1,HU Ze-peng2,TANG Si-long3,WAN Qun2
(1.Radio Monitoring Station of Jilin Province,Changchun130000,China;2.School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China;3.Tongfang Electronic Science and Technology Co.,Ltd.,Jiujiang 332007,China)
Understanding,analyzing and processing signals and data in high-dimensional space is an important method of modern signal and information processing.In this way,we can simplify the original problem to how to either determine or optimize linear relationship between dots,line and surface,and to overcome the problems such as performance analysis and practical implementation caused by nonlinear processing.However,we are often encountered with the absence of a part of signal and matrix elements in practice,which increases the difficulty of the subspace analysis.In this paper,we studied the subspace method of incomplete matrix and its applications to target localization through a few simple examples and provided the methods of performance optimization and resource optimization.
incomplete matrix;subspace analysis;target localization
赵琦,胡泽鹏,汤四龙,等.非完整矩阵的分析及其在目标定位中的应用[J].四川兵工学报,2015(11):95-97.
format:ZHAO Qi,HU Ze-peng,TANG Si-long,et al.Incomplete Matrix Analysis and Its Application to Target Localization[J].Journal of Sichuan Ordnance,2015(11):95-97.
TN957
A
1006-0707(2015)11-0095-03
10.11809/scbgxb2015.11.025
2015-05-04
国家自然科学基金(61172140)
赵琦(1972—),男,高级工程师,主要从事无线通信及信号监测研究。

