改进Friese光致旋转理论的模拟及实验分析

魏 勇,朱艳英

(1.燕山大学理学院,河北 秦皇岛 066004；2.燕山大学里仁学院,河北 秦皇岛 066004)



·光电技术与系统·

改进Friese光致旋转理论的模拟及实验分析

魏 勇1,2,朱艳英1

(1.燕山大学理学院,河北 秦皇岛 066004；2.燕山大学里仁学院,河北 秦皇岛 066004)

为验证改进Friese光致旋转理论的合理性和可靠度,搭建了实时、快速测量单轴双折射样品粒子转动情况的光镊实验平台。捕获激光微束首先被聚光镜收集,经二向色镜和成像透镜后被四象限探测器接受,四象限探测器的信号变化反映了微观物体在囚禁光阱的运动情况,然后使用数据采集卡采集四象限探测器的信号,最后通过信号和图像处理分析得到样品粒子的运动情况,并把实验结果与理论分析对比。结果表明,改进Friese理论的模拟曲线与测得的实验数据更相符。该激光光镊系统可用于驱动微纳机械装置、测量微纳系统的力学参数以及组装生物器件等。

物理光学；光镊；光致旋转；自旋角动量

1 引 言

近些年来,机器人学及自动化技术的研究和发展已经对现代制造工业产生了非常大的影响,而生物学和纳米技术的进步则导致机器自动化技术在微纳米设计方面的需求,因此,细胞或者微纳米颗粒的控制和操纵成为了人们所关注的焦点问题之一。目前,已经研究出许多显微操纵技术来满足各种不同的实际需求,例如微定位技术[1]和显微注射技术等[2],在这些技术中,激光光镊系统在实验室中的应用性和可靠性最为突出。激光光镊系统可以对微小颗粒(诸如原子、分子、细菌、病毒和活细胞等)进行实时动态的、几乎无损害的控制和操纵[3],因而被成功地应用于生物物理科学和纳米科技等领域来实现各类的微操纵及微加工任务,如生物细胞之间的分离[4],通过移动活的分裂神经元来评估不粘连的基元[5]以及DNA机械和结构性质的研究等[6]。另外,Friese等人通过计算建立了光致旋转的理论模型,可以使得捕获样品粒子在入射激光微束的作用下进行不同方向的平动和旋转,继而为周边各种形状转子的运动提供动力,这种模型为国内外学者研究微纳型马达转子技术的实现提供了理论和实验上的支持[7]。我们课题组在原有Friese等人提出的光致旋转理论基础上,分析了其理论的不完善之处,充分考虑了各种光学因素对样品粒子旋转的影响,推导出了改进的Friese理论模型[8],但尚未对该理论进行实验上的进一步验证。

本文首先基于模型仿真分别对微粒光致旋转的传统Friese理论和改进Friese理论进行了分析,然后利用自行搭建的激光光镊系统测量并讨论了样品粒子的转动情况,最后通过实验结果与理论模拟的比较来论证改进Friese理论模型的准确性与否。

2 改进光致旋转的理论模型

具有偏振特性的激光束沿着直线传播(z轴方向)可分解为[9]：

(1)

其中,EL和ER分别为左旋和右旋圆偏振光的复振幅;k为波矢量;ω表示圆频率。

基于晶体波动光学理论推导出碳酸钙晶体(负晶体)和石英晶体(正晶体)粒子的转动频率f1和f2分别为[8]：

(2-ro2-re2)}

(2)

(2-ro2-re2)}

(3)

其中,Pe为囚禁光阱中捕获激光的有效功率；η是溶液的粘滞系数;r和d为粒子的半径和厚度;α为激光束波矢方向与能流方向之间的夹角;re和ro分别是双折射样品粒子中e光和o光的反射系数;te和to分别是e光和o光的透射系数[8]。

传统Friese光致旋转理论中的晶体粒子转动频率为[10]

(4)

通过比较式(2)、式(3)和式(4)可以得出,传统的光致旋转理论对正负晶体的情况没有加以区分,并且没有考虑到晶面与光轴夹角、晶体表面的反射和透射率等因素对其转动频率的影响,而改进Friese理论模型考虑的因素则比较系统和全面。

3 仿真结果的分析比较

通过仿真对传统的Friese理论和改进的Friese理论进行比较,模拟有关条件参数如下:捕获激光功率为12 mW,波长为650 nm。由于实验中所配置的样品溶液浓度极低,所以取其粘滞系数为η=0.894×10-3N·m-2·s-1(实验环境温度为25 ℃)。碳酸钙晶体的主折射率为no=1.6557和ne=1.4852,石英晶体的主折射率为no=1.5427和ne=1.5518。图1和图2表示传统Friese理论和改进Friese理论优化下碳酸钙和石英晶体粒子的转动频率随半径的关系曲线比较。

图1 传统Friese理论和改进Friese理论下碳酸钙粒子的转动频率比较

由图1和图2可以看出,通过传统Friese理论和改进Friese理论计算所得出的转动频率值f都会随晶体粒子半径r的增大而迅速减小,但是对同一半径的不同样品粒子来说,其各自得到的转动频率值可能有所不同。对于碳酸钙粒子,当其半径在 1～4.5 μm范围时,传统Friese理论的转动频率最大值为351 Hz,远大于改进Friese理论值,二者区别较大；当粒子半径大于4.5 μm时,两理论所得到的模拟曲线基本一致。对于石英粒子,当其半径在1～5 μm时,传统Friese理论转动频率的最大值为107 Hz,是改进理论值的7.1倍；而当半径r大于5 μm 时,两理论所得的转动频率值基本趋向一致。由以上分析可得两理论主要在半径较小时差别比较显著,为进一步说明改进Friese理论的合理性,我们从光致旋转实验加以证明。

图2 传统Friese理论和改进Friese理论下石英粒子的转动频率比较

4 激光光镊系统

激光光镊系统原理如图3所示。本实验将光纤数字技术与显微成像系统结合,由光纤耦合半导体激光器,扩束准直器,二向色镜分光模块,CCD相机模块,显微物镜,三维精密载物台,光镊测力模块(QD),数据采集卡以及计算机等仪器构成。

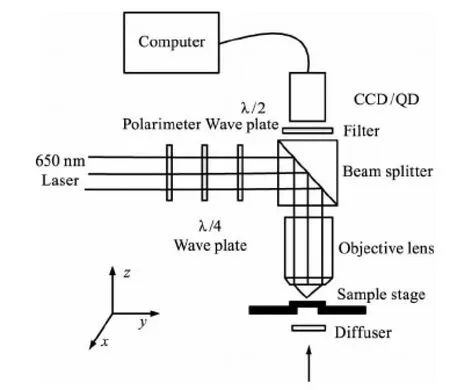
图3 激光光镊原理图

通过激光作用于微观物体(碳酸钙粒子或石英粒子)并将其捕获,作用过程通过显微成像系统经CCD相机和控制软件输入计算机,并由四象限探测器记录囚禁于光阱中物体的位置信息进行光阱力测量。操作者可通过显示器对样品进行观察,控制三维精密移动载物台使激光准确作用于目标微粒,可以对捕获目标微粒进行操控,通过计算机控制软件可将样品的动/静态变化过程存入硬盘,分析处理最后计算样品粒子的旋转频率[10]。

5 实验数据与理论对比

图4是用激光光镊对CaCO3样品粒子的捕获和操作照片,微粒半径为3.2 μm,厚度为1.3 μm左右,然后取了各种不同半径的样品粒子测量其转动频率值。图5和图6分别表示碳酸钙和石英样品粒子的改进Friese理论曲线和实验拟合曲线的比较关系。

图4 厚度为1.3 μm,半径为3.2 μm的碳酸钙样品粒子转动过程

从图5和图6中可以看出,测量的实验结果和改进Friese理论值基本取得一致。无论是碳酸钙或者石英样品粒子,它们的转动频率实验值都随半径的增大呈现减小的趋势。当粒子的半径为1 μm时,碳酸钙粒子和石英粒子转动频率的实际最大值分别为25.2 Hz和11.5 Hz。当样品粒子半径较大(3.5～6 μm)时,两曲线吻合情况较好。而当粒子半径较小(1～3.5 μm)时,二者有较小的差别,表现为传统Friese理论转动频率值比改进理论值略大。经分析主要原因是样品池中的粒子对入射光束具有吸收特性、溶液温度变化以及局域浓度不均匀等造成的。另外,由于一般情况下碳酸钙样品粒子的频率高于石英粒子,为增大微型机器自动化技术中机械转子的转速,选材方面应尽可能采用碳酸钙粒子制成微纳转子较好。从以上分析可以得出,与传统Friese理论的转动频率值(如图1和图2)相比,改进Friese理论值与实验数据明显更相符,二者曲线基本吻合,进一步说明了改进Friese理论的正确性。

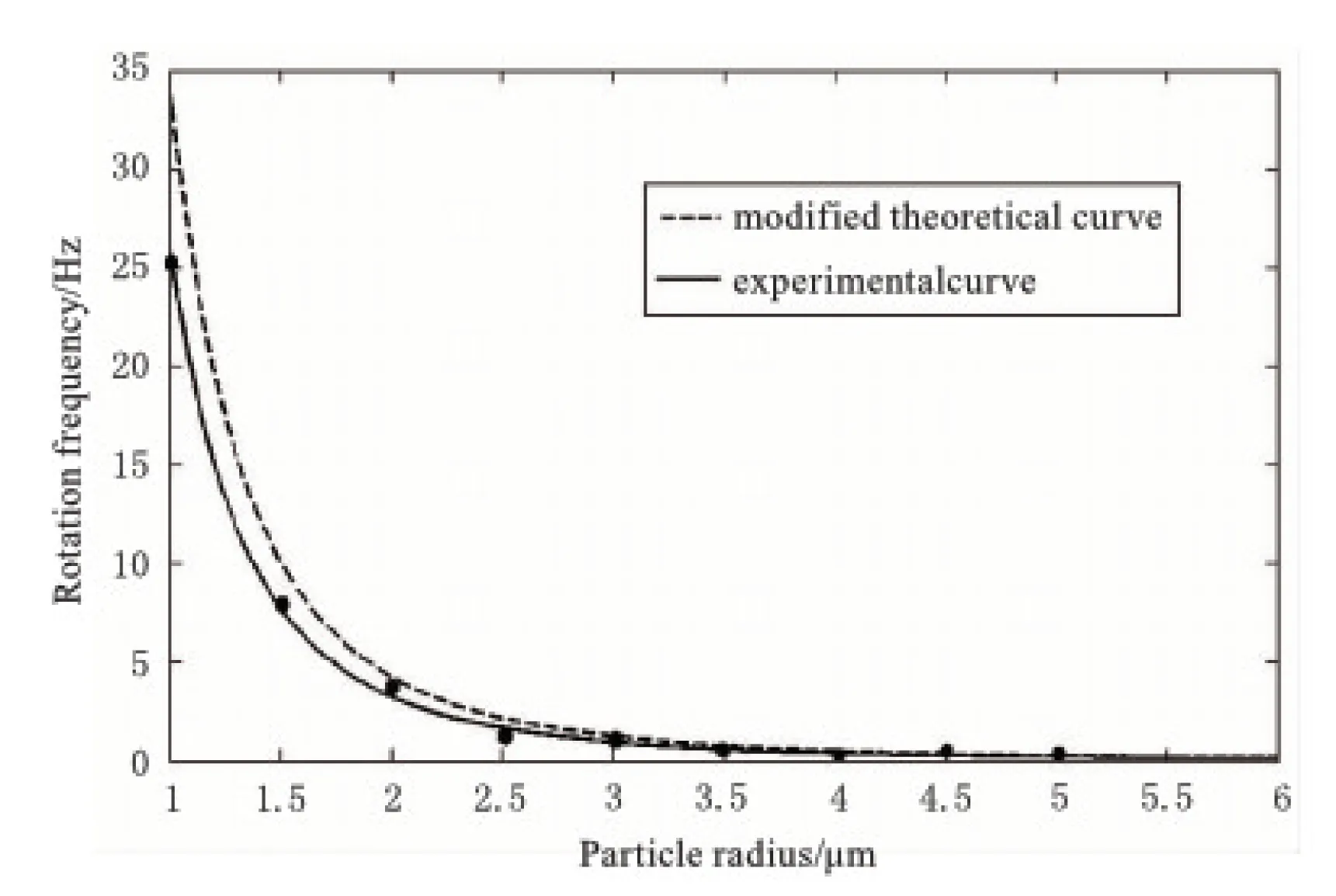
图5 碳酸钙样品粒子的改进Friese理论曲线和实验拟合曲线的比较

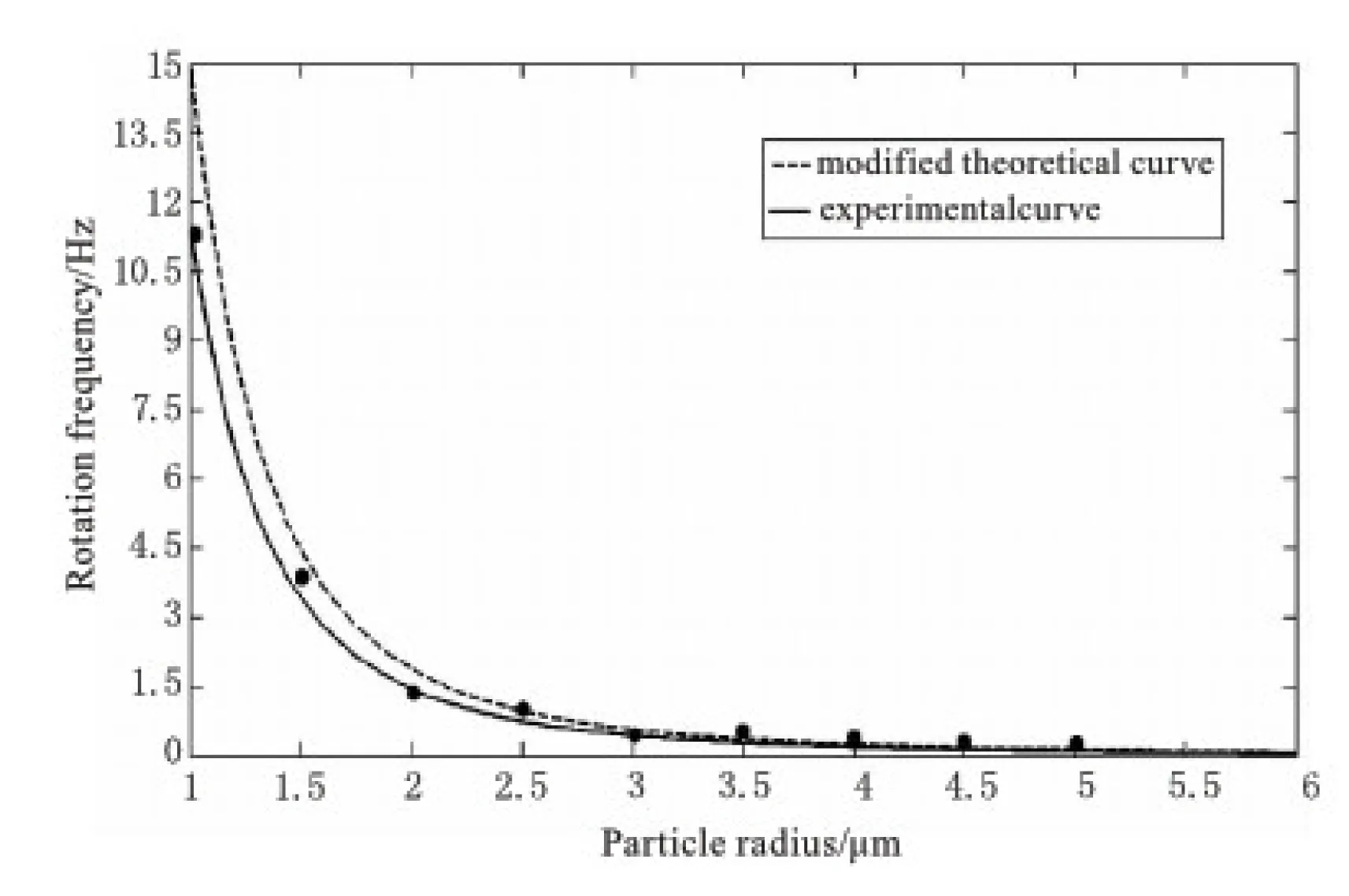
图6 石英样品粒子的改进Friese理论曲线和实验拟合曲线的比较

6 结 论

通过对传统光致旋转理论和改进Friese理论分别进行模拟分析并与实验对比研究,结果表明改进Friese理论的模拟曲线与实验数据基本相符,从而验证了该理论模型的正确性,这为微型机器结构设计中转子运动的精确测量提供了可靠的理论和实验保障；同时,把该光镊实验平台与荧光光谱技术相结合,可以实现各种样品细胞结构的可视化操纵、快速分析及其性质变化的研究等。

[1] LI Xiaotian,YU Haili,QI Xiangdong,et al.300 mm-travel stage of grating ruling engine and its self-adaptive control method[J].Chinese Journal of Lasers,2014,41(6):0608001.(in Chinese)

李晓天,于海利,齐向东,等.光栅刻划机300mm行程工作台研制及其自适应控制方法[J].中国激光,2014,41(6):0608001.

[2] TIAN Guizhong,CHEN Tao,WANG Shuyan,et al.Research progress on auto-microinjection technology in bio-engineering[J].Micronanoelectronic technology,2011,48(8):536-542.(in Chinese)

田桂中,陈涛,王淑妍,等.生物工程中自动化显微注射技术研究进展[J].微纳电子技术,2011,48(8):536-542.

[3] A Ashkin,M Dziedzic,E Bjorkholm,et al.Observation of a single-beam gradient force optical trap for dielectric particles[J].Optics Letters,1986,11(5):288-290.

[4] LI Yan,GUO Zhongyi,QU Shiliang.Living cell manipulation in a microfluidic device by femtosecond optical tweezers[J].Optics and lasers in engingeering,2014,55(3):150-154.

[5] P Christopher,G Alexander,W Wolfgang,et al.Microfluidic growth chambers with optical tweezers for full spatial single-cell control and analysis of evolving microbes[J].Journal of microbiological methods,2013,95(4):470-476.

[6] SHEN Junfeng,ZHANG Cuijiao,ZHANG Yuquan,et al.Study on novel nano-heating source based on plasmonic nanotweezers[J].Acta Optica Sinica,2014,34(9):0924001.(in Chinese)

沈军峰,张翠娇,张聿全,等.基于表面等离激元光镊的新型纳米热源研究[J].光学学报,2014,34(9):0924001.

[7] M E J Friese,T A Nieminen,N R Heckenberg,et al.Optical alignment and spinning of laser-trapped microscopic particles[J].Nature,1998,394:348-350.

[8] ZHU Yanying,WEI Yong,SHEN Junfeng,et al.The theory studies and simulation of optical rotation of uniaxial crystal particle[C].ISPDI 2011 China Orgainzing Committee,2011.

[9] A T Nieminen,N R Heckenberg,H Rubinsztein-Dunlop.Optical measurement of microscopic torque[J].J.Mod.Opt,2001,48(2):405-413.

[10]WEI Yong,ZHU Yanying,XIAO Changjiang.Effect of the thickness of the crytal particle on optaical rotation frequency[J].Laser & Infrared,2014,44(10):1095-1099.(in Chinese)

魏勇,朱艳英,肖长江.光致旋转中晶体微粒厚度对旋转频率的影响[J].激光与红外,2014,44(10):1095-1099.

Numerical simulation and experimental analysis on optical rotation of modified Friese model

WEI Yong1,2,ZHU Yan-ying1

(1.College of Science,Yanshan University,Qinhuangdao 066004,China；2.College of Liren,Yanshan University,Qinhuangdao 066004,China)

In order to verify the rationality and reliability of the theoretical model of modified Friese optical rotation,a real-time and rapid experimental platform of optical tweezers was set up to measure the rotation of uniaxial birefringence particles.The laser microbeam was firstly collected by collecting lens,and then the beam was collected by four-quadrant detector(QD)across dichroic mirror and imaging lens.The signal of four-quadrant detector was collected with data acquisition card.Finally,rotation frequency of sample particles was measured through the analysis of signal and image data,moreover,the analysis and comparisons with theoretical curves were presented in detail.The results show that,the simulation curve of modified Friese model is much consistent with the experimental data.The optical tweezer can be applied to drive micro-nano mechanism,measure mechanical parameters of micro-nano system and assemble biological devices.

physical optics;optical tweezers;optical rotation;spin angular momentum

1001-5078(2015)10-1221-04

国家自然科学基金项目(No.50875232)资助。

魏 勇(1982-),男,博士研究生,讲师,主要从事光微操纵技术和生物大分子测量方面的研究。E-mail:weiyongweiwei@163.com

2015-01-31

TN249

A

10.3969/j.issn.1001-5078.2015.10.015