高速永磁爪极电机铁耗与空气摩擦损耗计算

刘光伟 赵新刚 张凤阁 赵 鑫 Wenping Cao

（1.沈阳工业大学电气工程学院 沈阳 110870 2.Queen’s University Belfast Belfast BT9 5AH U.K.）

1 引言

高速电机作为高速驱动系统的核心部件，具有体积小、效率和功率密度高、一体化程度好等突出优点，已成为高端装备制造领域研究热点之一。在飞轮储能系统、石化产品加工、高速机床主轴电机等领域应用前景广阔[1-3]。

高速永磁爪极电机（HPCM）不仅具有效率和功率密度高的特点，与同功率常规电机相比体积小、重量轻，此外该电机还继承了常规爪极电机所具有的结构简单和成本低等优点，该电机爪极部分采用软磁复合材料（Soft Magnetic Composite，SMC）制成，该材料具有低涡流损耗、各向同性、可加工成任意形状的优点，特别适合应用于高速爪极电机[4-6]。该结构由澳大利亚悉尼工业大学的学者提出，并针对SMC 材料特性、等效磁路模型建立和损耗分析等方面开展了较多研究工作[7]。另外，瑞典The Royal Institute of Technology 对高速永磁电机的设计理论和方法进行了深入的研究，研制了20kW 转速高达100 000r/min 的样机，并进行了系统实验研究[8]；浙江大学对高速永磁无刷直流电机转子涡流损耗以及无位置传感器控制方面进行了深入研究，目前已经研制出2.3kW 高速永磁无刷直流电机[9]。

本文针对高速永磁爪极电机损耗较大发热严重的问题，基于有限元软件分析电机内部的磁场特点，建立考虑三维磁场分布的铁耗计算模型，并通过有限元和实验方法验证了计算模型的准确性；此外，针对高速电机转子表面线速度较高的特点，利用三维流体场对转子空气摩擦损耗进行分析，并与传统解析法比较，研究了空气摩擦损耗与电机转子转速、表面粗糙度及轴向风速的关系，为高速永磁爪极电机的设计与分析提供依据。

2 结构特点与运行原理

高速永磁爪极电机可采用单段、两段、三段或多段式结构，分别称为单相、两相、三相或多相电机。作电动机运行时必须采用两段、三段或多段式结构，以产生方向恒定的电磁转矩[10,11]。本文所研究的电机采用轴向三段式外用磁转子结构，每段由一组永磁外转子和爪极定子组成，其结构如图1 所示。电机外转子内表面粘贴永磁体，定子爪极由两片法兰型爪极磁轭装配形成，每片爪极磁轭由多个沿周向方向均匀分布的爪极与圆盘型磁轭组成，将两片爪极磁轭装配组成形状类似圆饼型的定子爪极铁心。单相定子集中绕组放置于定子爪极铁心内部，均匀缠绕在两片爪极磁轭之间的定子内轴上，从而形成单段式高速爪极电机。将三个单段式爪极电机沿轴向组装形成三段式结构爪极电机，为了产生恒定电磁转矩，将三段定子爪极互错120°电角度装配，外转子永磁体沿轴向同位置安装。当三相对称电流通入各相绕组时，形成互差120°的定子磁场，它们分别于转子永磁体产生的主磁场相互作用，形成恒定电磁转矩。

图1 高速永磁爪极电机结构示意图Fig.1 The structure diagram of HPCM

3 铁耗计算

3.1 三维磁场分析

高速永磁爪极电机定子铁心内部磁场呈三维分布，电机运行时铁心的磁化方式应该既包括交变磁化又包括旋转磁化，且各部分磁化情况不同，因此有必要对电机铁心各部分磁场的规律进行分析，电机定子铁心剖面图如图2 所示。

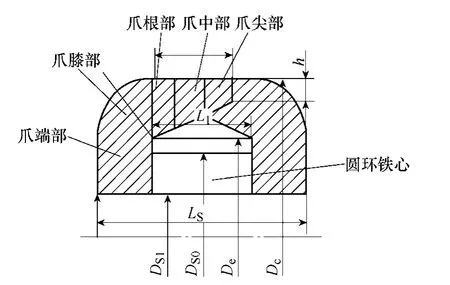
图2 电机定子铁心剖面图Fig.2 The sectional diagram of stator

从图2 可知，电机定子铁心分可为六部分：爪端部、爪膝部、爪根部、爪中部、爪尖部和圆环铁心。通过三维磁场有限元软件计算单个周期内各部分磁场分布情况，对每部分多个位置的磁通密度变化情况进行分析，得到能够反映各部分三维磁场分布的关键点的三维磁通密度分布变化曲线，为了避免重复赘述，文中只给出了爪端部、圆环铁心和爪中部的三维磁通密度变化结果，如图3 所示，图中各部分磁通密度变化轨迹的形状和变化规律均不相同，即各部分磁通密度变化情况亦不相同，因此在计算铁耗时必须对各部分磁通密度变化分别考虑然后进行计算。

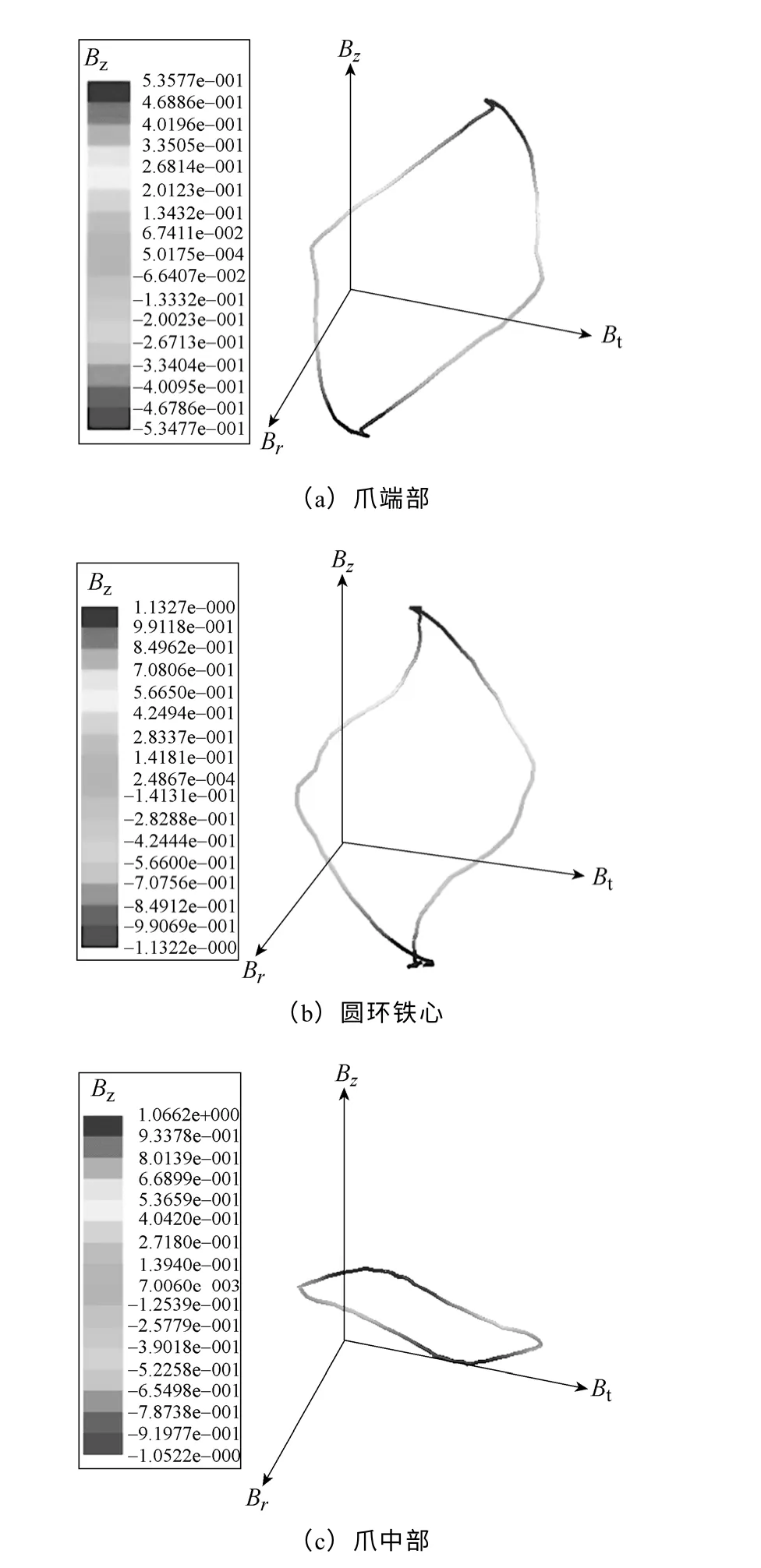
图3 定子铁心各部分三维磁通密度Fig.3 The three-dimension flux density results of stator

3.2 铁耗计算模型

目前应用比较普遍的是Bertotti 铁耗分离模型，它将铁磁材料损耗分为三部分：磁滞损耗、涡流损耗和附加损耗。该模型不考虑局部磁滞环的影响，认为涡流损耗与磁场幅值、频率和波形均有关，而磁滞损耗与磁场波形无关，该模型只考虑了交变磁化引起的铁心损耗，计算方法简单但误差较大[12]。

悉尼科技大学研究了考虑旋转磁化计算模型的电机铁耗计算方法，通过旋转铁耗测试仪进行大量实验以确定定子铁心在旋转磁化下的损耗系数，在此基础上采用曲线拟合的方法，建立了圆形旋转磁化铁耗模型。该方法需对样机进行大量实验获取损耗系数且通用性尚无法得到验证，因此采用该方法的仍有一定难度和制约[13]。

由于旋转铁耗计算模型的局限性，计算准确性和精度都达不到理想情况，因此本文提出用三维正交交变磁化来等效替代旋转磁化的方法，即把磁场分解成径向、切向和轴向分量分别进行铁耗计算，然后将三部分的铁耗值相加得到总铁耗。实际电机中的磁场并不是真正的圆形磁场，因此各方向磁通密度可分解成一系列的谐波磁通密度，将基波及各次谐波产生的铁耗相加即得到任意磁化波形下的铁耗，此方法不仅能够计算交变磁化和旋转磁化两种磁化影响下的铁耗，还考虑了谐波磁场对铁耗值的影响，而且损耗系数只需要用在交变磁场下测得的损耗曲线拟合得到，无需精密的测试仪器，计算精度较高，实用性较强。

设任意磁场为B(t)，可将其正交分解为

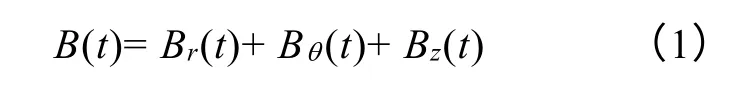
式中，Br(t)、Bθ(t)和Bz(t)分别为磁场磁通密度值的径向、切向和轴向分量。

磁滞比损耗为

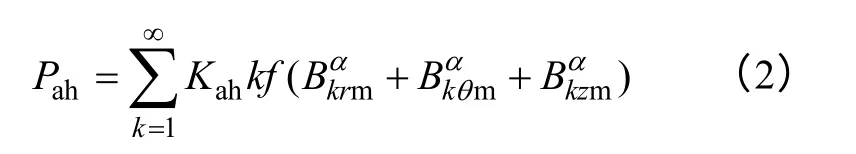
涡流比损耗为

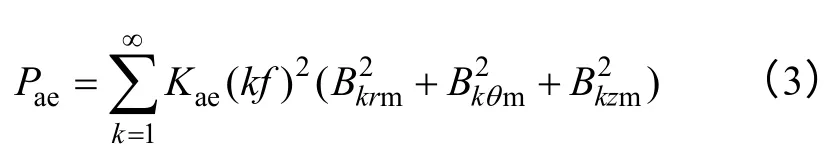
附加比损耗为

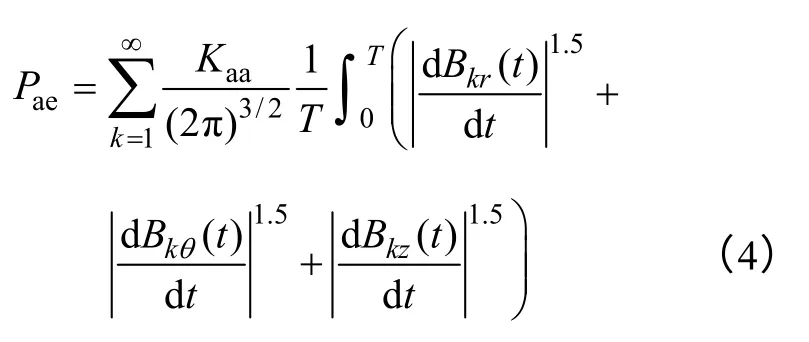
式中，下标k、m 分别为k次谐波分量和幅值；Kah、Kae、Kaa和α分别为磁滞损耗系数、涡流损耗系数、附加损耗系数和材料磁系数。

根据SMC 材料厂家提供的交变磁化下的损耗曲线，利用最小二乘法进行拟合得到铁耗计算模型中的磁滞损耗系数、涡流损耗系数、附加损耗系数及材料磁系数见下表。

表 损耗系数拟合值Tab. The fitted values of loss coefficient

3.3 铁耗计算结果

在确定了各损耗系数与定子铁心关键位置磁通密度分布后，根据上述考虑三维正交磁化和谐波影响的铁耗计算模型可计算该电机定子铁耗，在不同条件下单段电机的铁耗计算结果如图4 所示。该模型的铁耗计算结果较有限元方法高出10%左右，考虑谐波旋转磁化时得到的铁耗值更接近于实际电机测试结果，且随频率基本呈线性增长，这与SMC材料生产厂商给出的铁耗特性相吻合，进一步验证了计算模型准确性。

图4 不同条件下铁耗计算结果Fig.4 Iron loss results for different conditions

4 空气摩擦损耗计算

空气摩擦损耗的产生机理是由于空气与转子存在相对运动，二者相互滑动摩擦产生的。由于高速电机转速较高，其相对运动速度远高于常规电机，因此其空气摩擦损耗占总损耗比值非常大，有必要对其进行分析[13,14]。空气摩擦损耗与转子表面结构、空气流速、电机转速、转子表面粗糙度和空气径向压力等因素有关。

圆柱体表面空气摩擦损耗计算公式如下[15]：

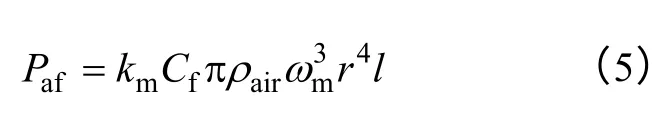
式中 km——转子表面粗糙度系数；

Cf——摩擦系数；

ρair——空气密度；

ωm——圆柱体旋转角速度；

r，l——圆柱体轴向长度和半径。

电机摩擦系数Cf可通过下式求得

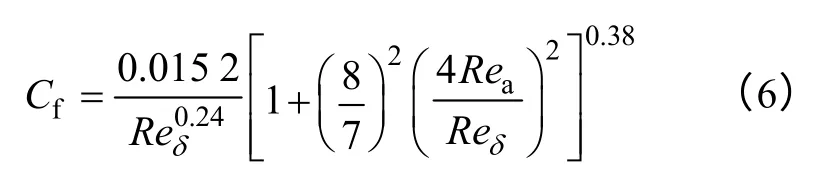
式中

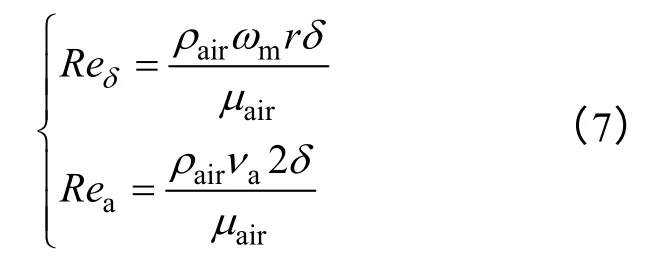
式中 δ——气隙径向长度；

va——轴向强迫风冷的风速；

μair——空气运动粘度。

但是，由于永磁体四个侧表面均为径向面，电机高速旋转时空气在此处的流动路径较为复杂，除了轴向、切向运动外，空气还会在永磁体处遇阻沿径向流动，所以用式（5）很难直接精确计算出空气摩擦损耗。本文采用流体场计算软件对定转子间风路区域进行温度场计算，利用软件计算热流量值从而间接得到空气摩擦损耗[13,16]。

图5 和图6 分别为旋转域中电机转子内表面温度分布图和通风道中热流量分布图。从图5 中可以看出，转子内表面温度从进口处至出口处沿轴向逐渐增高，相邻永磁体间缝隙内温度较周向其它部位略高，因为空气在永磁体侧面流动路径复杂，并非单一的轴向直线运动与周向旋转运动，还包括其它不规则流动形式，将会产生较多的摩擦损耗，使得该位置温度增高，因此需采用永磁体缝隙填充和改善转子内表面光滑度等方式减少摩擦损耗；从图6中可以看出热量运动规律，大致可分为轴向、切向以及任意合成方向运动形式，进一步验证了上面中转子内表面温度分布特点的分析。

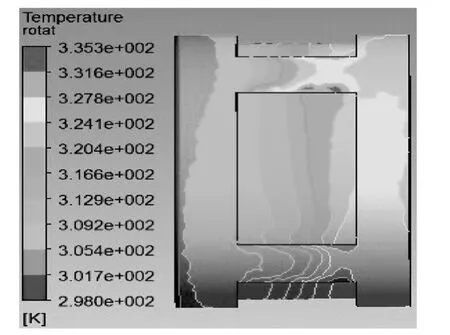
图5 转子内表面温度分布图Fig.5 Temperature distribution at inner surface of rotor

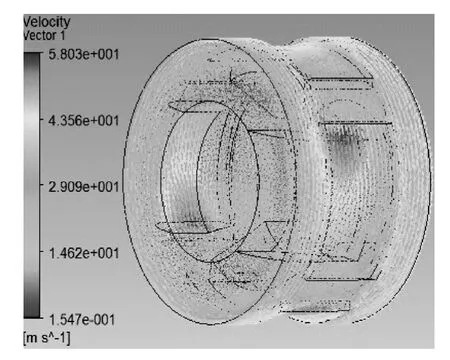
图6 通风道中热流量分布图Fig.6 Heat flow distribution in ventilation duct

由于空气摩擦损耗与转子内表面永磁体放置有关，为了使转子内表面更加光滑在相邻永磁体填充环氧树脂，通过计算得到填充环氧树脂后空气摩擦损耗为94W，而不填充时为138W，显然永磁体间填充环氧树脂可大幅减小空气摩擦损耗。

转子空气摩擦损耗除了与电机转速有关之外，还与转子表面的粗糙度和轴向风速等因素有关。根据流体场分析结果，可以得出上述三个因素对空气摩擦损耗的影响，其结果分别如图7～图9 所示。

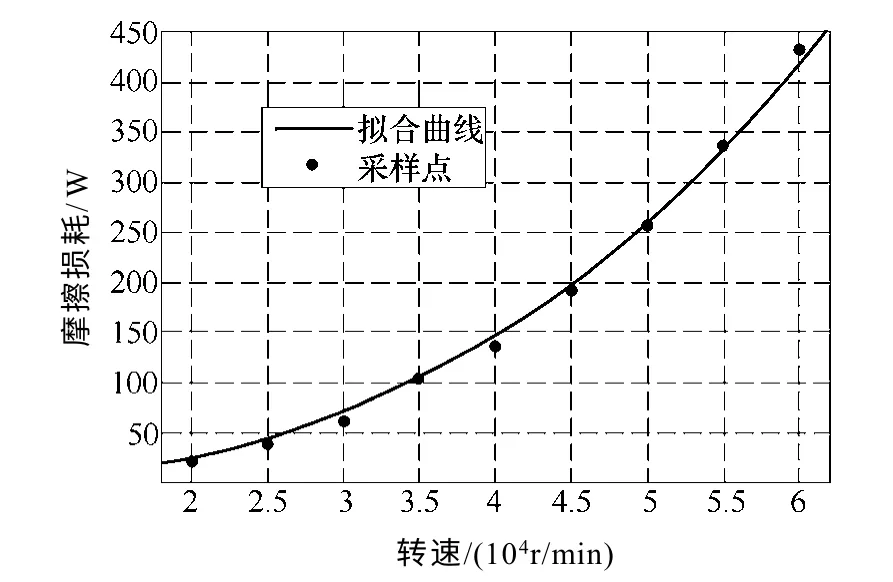
图7 空气摩擦损耗和转速的关系Fig.7 Relationship between air friction loss and speed

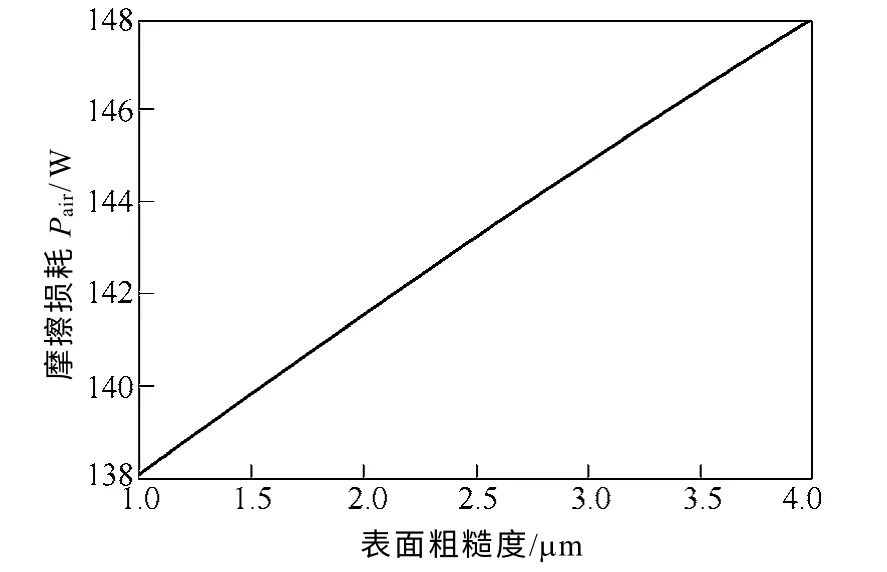
图8 转子表面粗糙度与空气摩擦损耗的关系Fig.8 Relationship between air friction loss and rotor surface roughness

图9 轴向风速与空气摩擦损耗的关系Fig.9 Relationship between air friction loss and air axial speed

从图7～图9 可以看出，与转子表面粗糙度相比对空气摩擦损耗影响更大的是电机的转速，基本呈现指数增长的趋势，虽然增加轴向风速有利于带走电机的一部分热量，但是同时增加了空气摩擦损耗，因此应在尽量减小转子内表面粗糙度的同时，适当选取轴向风速。

5 实验研究

图10 电机测试系统Fig.10 Machine test system

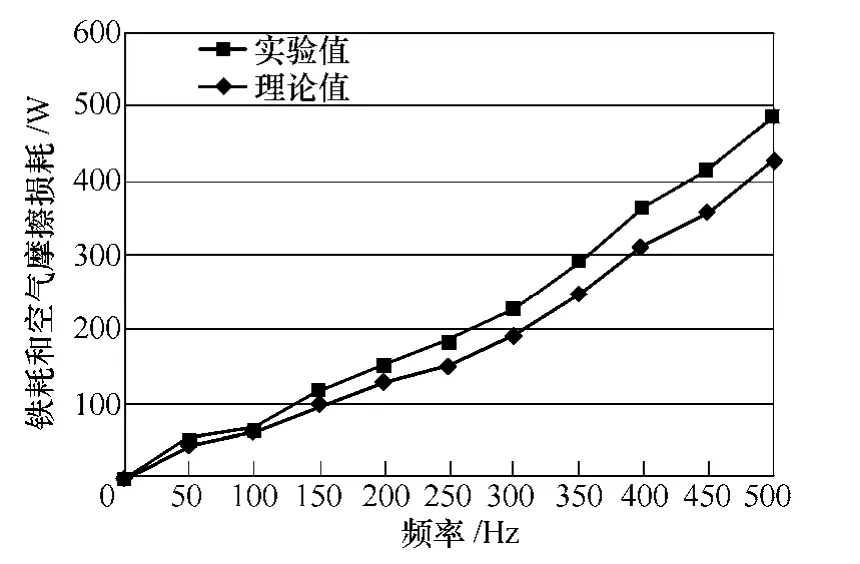
图11 电机损耗理论计算值与实验值对比Fig.11 Comparision between theory and test results

为了验证所提出的铁耗与空气摩擦损耗计算模型的准确性，搭建了一套电机损耗测试系统，该系统组成如图10 所示。测试样机由原动机拖动旋转，测试在不同供电频率下电机的铁耗与空气摩擦损耗，实验结果与理论计算结果如图11 所示。在频率低于200Hz 时，理论值与实验值吻合较好，误差小于10%，但是随着频率和转速增加，两者误差逐渐增大，一方面因为损耗计算模型中的部分参数可能在高频条件下设置不准确，另一方面随转速升高使得测得结果中机械摩擦损耗占比增加，引起测试结果误差。

6 结论

本文通过磁场有限元分析和流体场温度计算对高速永磁爪极电机的铁心损耗和空气摩擦损耗进行研究，得到如下结论：

（1）电机定子铁心内部磁场呈三维分布，且各部分均不形同，在充分考虑各部分三维磁场和谐波影响的基础上，建立了能够较准确反应高速爪极电机铁心损耗的铁耗计算模型。

（2）通过计算定转子间通风道温度分布间接得到电机空气摩擦损耗，并分析了电机转速、转子表面的粗糙度和轴向风速等因素对空气摩擦损耗的影响。

（3）通过搭建实验平台并进行实验研究，验证本文所提出的损耗计算方法的准确性，为高速永磁爪极电机优化设计提供了理论参考依据。

[1]Borisavljevic A,Polinder H,Ferreira A.On the speed limits of permanent-magnet machines[J].IEEE Transactions on Industrial Electronics,2010,57(1):220-226.

[2]Jang S M,Cho H W,Choi S K.Design and analysis of a high-speed brushless DC motor for centrifugal Compressor[J].IEEE Transactions on Magnetics,2007,43(6):2573-2575.

[3]Kolondzovski Z,Arkkio A,Larjola J,et al.Power limits of high-speed permanent magnet electrical machines for compressor applications[J].IEEE Transactions on Energy Conversion,2011,26(1):73-82.

[4]张凤阁,刘光伟,白海军.外永磁转子爪极电机磁路模型的建立与参数计算[J].电工技术学报,2012,27(6):19-24.Zhang Fengge,Liu Guangwei,Bai Haijun.Magnetic circuit model and parameter calculation of a claw pole machine with outer PM rotor[J].Transactions of China Electrotechnical Society,2012,27(6):19-24.

[5]王群京,倪有源,李国丽.爪极电机的结构、理论及应用[M].北京:中国科学技术大学出版社,2006.

[6]Jurca F N,Martis C.Theoretical and experimental analysis of a three-phase permanent magnet claw-pole synchronous generator[J].IET Electric Power Applications,2012,6(8):491-503.

[7]Guo Y G,Zhu J G,Lu H.Core loss calculation for soft magnetic composite electrical machines[J].IEEE Transactions on Magnetics,2012,48(11):3112-3115.

[8]Chudi P,Malmquist A.Development of a small gas Turbine-driven high-speed permanent magnet generator[D].Stockholm:The Royal Institute of Technology,2008.

[9]周凤争,沈建新,林瑞光.从电机设计的角度减少高速永磁电机转子损耗[J].浙江大学学报(工学版),2007,41(9):1587-1591.Zhou Fengzheng,Shen Jianxin,Lin Ruiguang.Reduction of rotor loss in high-speed PM motors by design method[J].Journal of Zhejiang University:Engineering Science,2007,41(9):1587-1591.

[10]乔东伟,王秀和,朱常青.新型混合励磁无刷爪极发电机的磁场调节特性分析及试验研究[J].中国电机工程学报,2013,33(9):115-121.Qiao Dongwei,Wang Xiuhe,Zhu Changqing.Investigation of flux regulation performance and experimental validation novel hybrid excitation brushless claw-pole alternators[J].Proceedings of the CSEE,2013,33(9):115-121.

[11]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.

[12]郭伟,张承宁.车用永磁同步电机的铁耗与瞬态温升分析[J].电机与控制学报,2009,13(1):83-87.Guo Wei,Zhang Chengning.Iron loss and transient temperature analysis of permanent magnet synchronous motor for electric vehicles[J].Electric Machines and Control,2009,13(1):83-87.

[13]黄允凯,朱建国,胡虔生.顾及旋转铁耗的高速爪极电机三维磁热耦合分析[J].电工技术学报,2010,25(5):54-60.Huang Yunkai,Zhu Jianguo,Hu Qiansheng.Magnetothermal analysis of a high-speed claw pole motor considering rotational core loss[J].Transactions of China Electrotechnical Society,2010,25(5):54-60.

[14]路义萍,李伟力,韩家德,等.大型汽轮发电机转子风道结构对空气流量分配影响[J].电工技术学报,2008,23(4):20-24.Lu Yiping,Li Weili,Han Jiade,et al.Effect of rotor’s cooling duct geometry on air mass flow rate distribution of large turbo generator[J].Transactions of China Electrotechnical Society,2008,23(4):20-24.

[15]孔晓光,王凤翔,邢军强.高速永磁电机的损耗计算与温度场分析[J].电工技术学报,2012,27(9):166-173.Kong Xiaoguang,Wang Fengxiang,Xing Junqiang.Losses calculation and temperature field analysis of high speed permanent magnet machines[J].Transactions of China Electro Technical Society,2012,27(9):166-173.

[16]Huynh C,Zheng Liping,Acharya D.Losses in high speed permanent magnet machines used in micro turbine applications[J].Journal of Engineering for Gas Turbines and Power,2009,131:1-6.