一种消除合成孔径雷达高度计延迟校正中残余误差的新算法及仿真验证
王 磊 许 可 史灵卫 杨双宝
一种消除合成孔径雷达高度计延迟校正中残余误差的新算法及仿真验证
王 磊*①②③许 可①③史灵卫①③杨双宝①③
①(中国科学院空间科学与应用研究中心 北京 100190)②(中国科学院大学 北京 100049)③(中国科学院微波遥感技术重点实验室 北京 100190)
合成孔径雷达高度计可以获得比传统雷达高度计更高的测量精度,延迟校正是其中的核心技术。在雷达收发脉冲的间隔内,由于卫星运动,目标与雷达之间的距离变化会带来残余误差,这点在现有的延迟校正算法中都未考虑。该文研究了垂直速度和水平速度对延迟校正的影响,建立了合成孔径雷达高度计的延迟校正模型,提出了一个新的延迟校正算法,消除了卫星垂直速度和水平速度带来的残余误差。最后通过计算机仿真进行了验证,仿真结果表明,该文提出的算法可得到准确的校正结果。
合成孔径雷达高度计;延迟校正算法;残余误差
1 引言
雷达高度计是一种海洋动力环境测量的卫星遥感仪器,它可以获得高精度的全球海面高度、有效波高和海面后向散射系数。合成孔径雷达高度计是新一代的雷达高度计,它在传统雷达高度计的基础上,提高脉冲重复频率并在顺轨向进行合成孔径处理,使得斜视观测也贡献于测高,从而提高了测量精度,同时提高了测量的分辨率。目前欧洲已发射运行的Cryosat-2卫星上的SIRAL雷达高度计是第1颗带有合成孔径模式的星载雷达高度计,国外学者对其合成孔径观测模式下的数据处理得到了比传统模式更好的结果;另外欧空局正在研制的Sentinel-3卫星雷达高度计SARL也是一台工作于合成孔径模式的雷达高度计[8]。我国也在积极研究合成孔径雷达高度计,并取得了一定的成果。
然而引入合成孔径技术以后,也相应地给数据处理带来了新的问题,比如回波模型、延迟校正算法与多视配准等。在这些问题中,延迟校正算法是其中的关键技术之一,合成孔径雷达高度计要获得高精度的测量结果,其前提是延迟校正的结果必须准确。目前关于合成孔径雷达高度计的延迟校正算法中,奠基性的算法是Raney[2]在1998年给出的。然而Raney算法只是根据多普勒频率对斜距进行了校正,忽略了在收发脉冲期间由于卫星运动带来的残余误差,也没有修正卫星垂直速度的影响。2014年,欧空局专门研究合成孔径雷达高度计技术的SAMOSA(Synthetic aperture radar Altimeter MOde Studies and Applications)项目组又公开了一个延迟校正算法[12],该算法在Raney的基础上校正了卫星垂直速度带来的多普勒频率的偏移,但对于在收发脉冲期间由于卫星运动带来的残余误差依然没有校正。
本文考虑了卫星的水平速度、垂直速度以及收发脉冲期间卫星运动导致的距离变化,建立了合成孔径雷达高度计延迟校正的完整模型,提出了一个新的算法,该算法消除了卫星运动带来的残余误差。最后仿真了合成孔径雷达高度计的点目标和面目标回波信号,并采用Raney算法、SAMOSA算法和本文算法对仿真数据进行处理,结果表明,Raney算法和SAMOSA算法的误差较大,而本文给出的新算法则可以准确地完成距离校正。
2 合成孔径雷达高度计的延迟校正算法
2.1延迟校正的目的
合成孔径雷达高度计在传统雷达高度计的基础上,在顺轨向引入了合成孔径处理之后,其等效足迹由圆环变成了垂直于雷达轨迹的条带[2]。为了使得斜视观测也贡献于测高,需要在多普勒条带内进行延迟校正。图1是延迟校正算法的示意图,图中是星下点,阴影部分是天线3 dB波束宽度的照射区域,虚线形成的条带是波束锐化形成的分辨单元,点是观测场景中的一个目标。当卫星运动到点附近时,高度计发射一个脉冲簇并接收回波海面的回波信号,延迟校正的目的就是将斜距校正成最短距离。
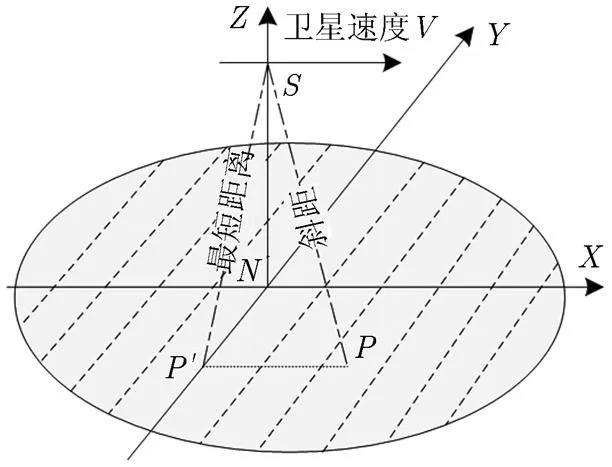
图1 延迟校正算法示意图
2.2 Raney算法和SAMOSA算法
Raney给出的延迟校正算法的基本流程是:合成孔径雷达高度计采用较高的脉冲重复频率(Pulse Repetition Function, PRF)发射脉冲信号,接收到回波信号后先进行全去斜处理,然后对I/Q信号进行2维存储;之后在顺轨向进行FFT变换以完成波束锐化[2,13];波束锐化之后,在各个多普勒频率单元内分别进行延迟校正;最后在距离向做傅里叶变换以完成距离压缩。上述数据处理流程可简单归纳为以下几个步骤[2]:
(1)全去斜;(2)2维数据存储;(3)顺轨向波束锐化;(4)延迟校正;(5)距离向压缩。
SAMOSA算法流程与Raney提出的数据处理流程基本相同,只是在Raney的基础上,在顺轨向FFT变换之前增加了多普勒中心频率偏移校正。
2.3水平速度与垂直速度的影响
然而Raney算法和SAMOSA算法都未考虑卫星运动带来的残余误差。图2是图1在交轨向侧视的细节示意,其中分别是雷达发射第1,第32,第64个脉冲时的位置,是接收第1,第32,第64个海面回波时的位置。在Raney算法和SAMOSA算法中,雷达脉冲的双程传播距离是发射脉冲传播距离的两倍,但如图2所示,卫星在发射脉冲和接收脉冲时的位置是不同的,需分别考虑脉冲的发射距离和接收距离。在卫星轨道高度为800 km时,卫星水平速度约为7.5 km/s,因地球椭球形状造成的垂直速度可达25 m/s,收发脉冲的间隔约为5.3 ms,在此时间段内水平速度带来的目标到雷达的距离变化可达到40 cm,垂直速度带来的距离变化可达到12 cm,这对于测量精度在厘米量级的高度计来说是很大的误差,必须校正。
在上述流程中,只是将合成孔径雷达高度计中的斜距校正成了最短距离,卫星垂直速度和水平速度带来的残余误差都没有校正。

图2 延迟校正细节示意
3 新的延迟校正算法
3.1 距离历史公式
为了得到准确的延迟校正公式,首先需要建立准确的距离历史公式。以雷达发射Burst中间时刻对应的星下点为坐标原点,雷达轨迹为轴,交轨向为轴,卫星指向星下点的方向为轴,建立发射信号和接收信号的距离公式:
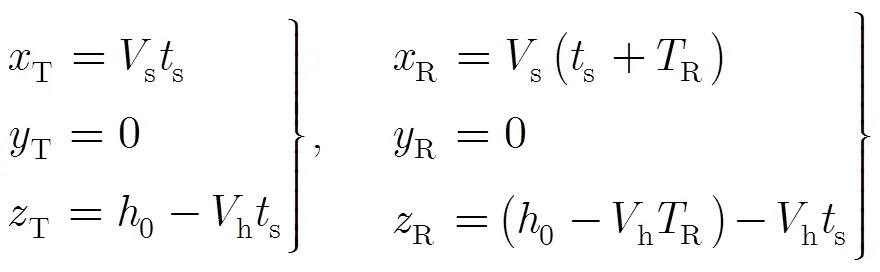

3.2 去斜后的回波信号
高度计先发射线性调频信号,然后将接收到的回波信号进行全去斜处理后得到了中频回波信号[14]:
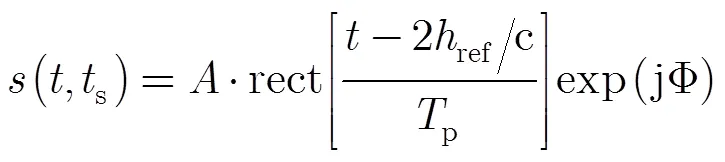

3.3残余误差的校正
延迟校正算法的下一步是顺轨向的波束锐化,在顺轨向做FFT即可完成[2,13]。波束锐化之后有两项需要校正,第1项是残余误差2;另一项是斜距误差,需要将斜距校正成最短距离。在这两项校正中都含有目标的顺轨向坐标,解出与多普勒频率的关系后即可完成斜距误差以及残余误差2的校正。
延迟校正算法的最后一步是距离向压缩[2,13],即在距离向做FFT变换,最终结果是一个2维的sinc函数:
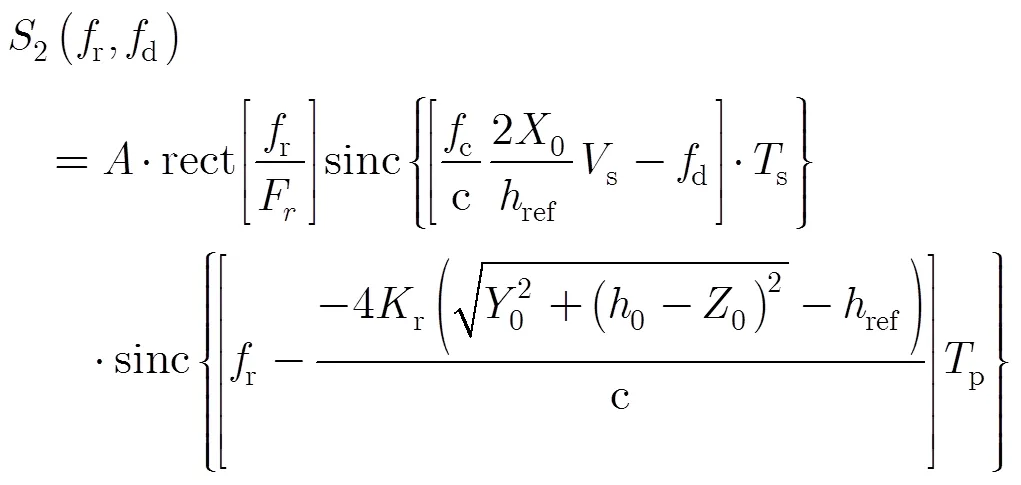
从式(5)可以看出,经过延迟校正以后点目标的回波信号被压缩成一个2维的sinc函数,在距离向的中心位置只与目标距离向的坐标和垂直高度有关,顺轨向的中心位置只与目标顺轨向的坐标有关。
4 仿真验真
为了验证上节给出的延迟校正算法,并与Raney算法及SAMOSA算法进行比较,本节对仿真点目标及面目标回波信号进行验证。对点目标回波信号,采用3种算法分别进行延迟校正,比较校正效果;对面目标回波信号,在延迟校正后进行回波重跟踪处理,比较重跟踪结果。
4.1 点目标回波信号仿真
设一排点目标排列在沿顺轨向的平面上,顺轨向的坐标从-10000 m变化到10000 m,交轨向的坐标都为0。卫星轨道高度为800 km,从坐标(0,0, 800000)开始匀速直线飞行,水平速度为7.5 km/s,垂直速度为25 m/s,雷达以Burst方式发射脉冲,簇内脉冲重复频率为18 kHz,连续发射个脉冲,脉冲宽度为。
图3是仿真数据延迟校正前后的示意图。图3(a)是回波信号不做校正直接在距离/多普勒域压缩的结果,图3(b)是Raney算法的校正结果,图3(c)是SAMOSA算法的校正结果,图3(d)是本文算法的校正结果。可以看出,不做校正时压缩以后目标在距离/多普勒域的排列呈抛物线状,而且由于垂直速度不为0,多普勒频率出现了偏移;Raney算法由于没有校正多普勒频率偏移,出现了很大的校正误差;SAMOSA算法校正后目标的位置出现了偏移,且不同多普勒频率的目标在距离向的偏移量不同,最大偏移量达到了0.5个距离门,误差大约为24 cm;不同多普勒频率的目标偏移量不同,这势必导致不同多普勒条带的回波前沿不能对齐,从而影响多视回波的形状,进而影响测量高度和有效波高;本文算法校正后,目标排列成一条直线,其中心位置都落在了0距离门处,得到了准确的校正。

图3 不同延迟校正算法的校正结果
4.2面目标回波信号仿真
面目标回波的仿真,首先需要仿真海面,并设计卫星的轨道参数。海面的仿真,本文参考文献[15~17]中的方法,采用风浪谱与涌浪谱叠加的方式来仿真,风浪谱采用文献[18]提出的模型,涌浪谱采用2维高斯模型,海面网格分辨率为;卫星轨道参数与点目标仿真时相同。根据仿真得到的海面散射点的高程数据和轨道数据计算出目标到雷达的距离,进而计算出回波信号的相位信息,将天线波束照射范围内所有目标的回波信号叠加就可得到面目标回波数据。
得到面目标回波信号的仿真数据以后,对仿真数据先采用3种延迟校正算法进行校正,然后多视配准,再进行重跟踪处理,最终得到海面的高度。其中回波重跟踪算法采用最小二乘算法,回波模型采用文献[19]给出的模型。下面分别是卫星垂直速度为0(有效波高为2 m)和卫星垂直速度为25 m/s(有效波高为4 m)这两种情况下仿真数据的处理结果。
4.2.1垂直速度为0,有效波高为2 m 图4(a)是采用本文算法得到的海面高度,图4(b)是SAMOSA算法得到的海面高度,Raney算法与SAMOSA算法结果相同。统计得到,关于高度的平均误差,本文算法为0.43 cm, SAMOSA算法为22.66 cm;关于标准差,本文算法为1.40 cm, SAMOSA算法为1.45 cm。另外,关于有效波高,本文算法的平均误差为4 cm, SAMOSA算法的平均误差为15 cm,标准差两者基本一致,都为9.0 cm左右。
4.2.2垂直速度为25 m/s,有效波高为4 m 图5(a)是采用本文算法处理得到的海面高度,图5(b)是SAMOSA算法得到的海面高度,Raney算法因未校正多普勒频率偏移而失效。关于高度的平均误差,本文算法为0.00 cm, SAMOSA算法为-5.96 cm;关于标准差,本文算法为1.97 cm, SAMOSA算法为1.96 cm。有效波高的平均误差,本文算法为1 cm, SAMOSA算法为13 cm;关于标准差两者基本一致,都为8.0 cm左右。
综上所述,仿真得到的面目标回波数据,本文算法和SAMOSA算法处理结果的标准差相当。然而SAMOSA算法存在一定的偏差,且偏差在垂直速度为0和25 m/s时不同。本文算法在垂直速度为0或者25 m/s的情况下都可以得到准确的结果。
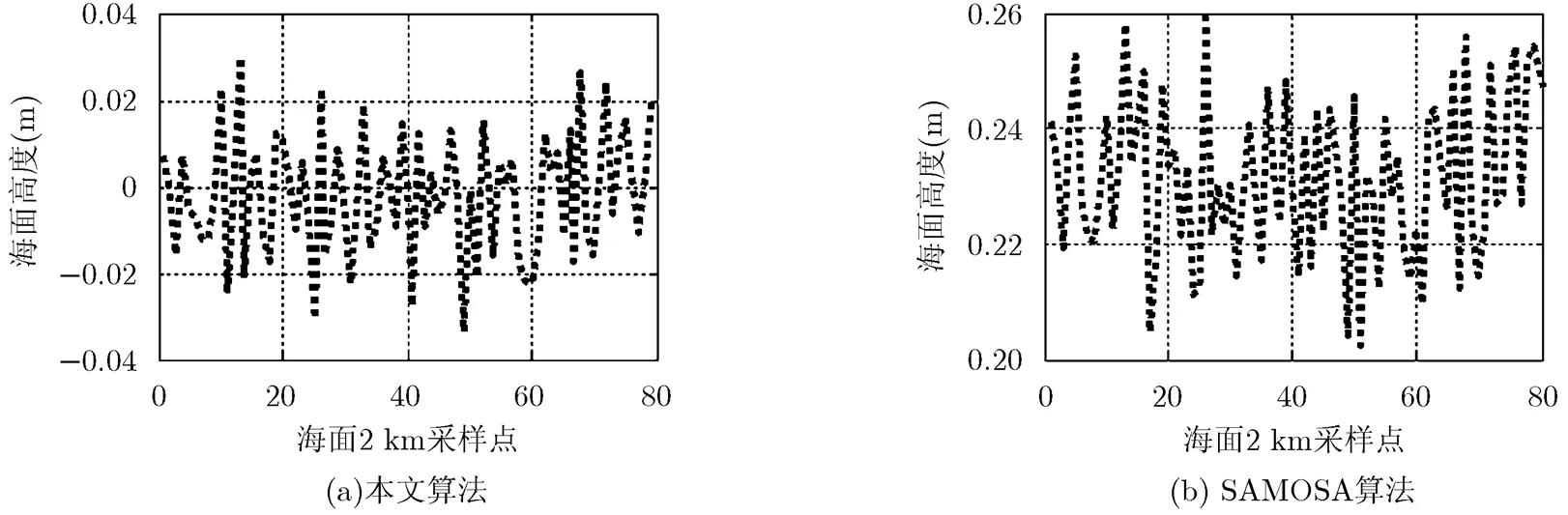
图4 垂直速度为0时,面目标回波信号处理结果
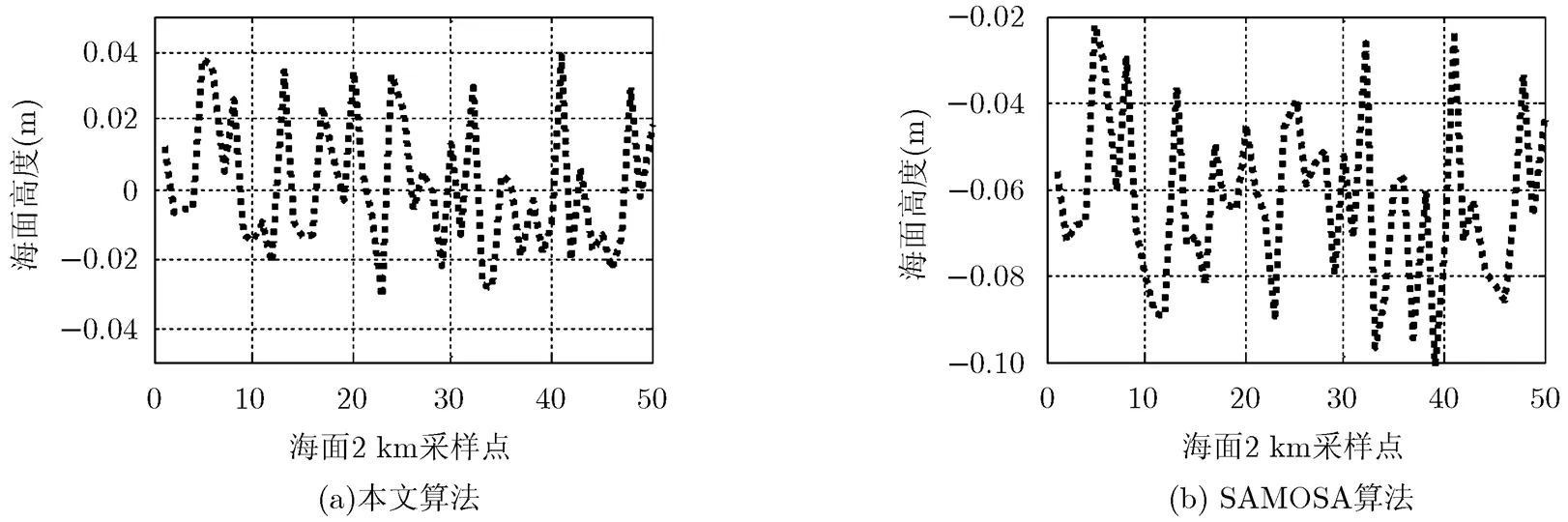
图5 垂直速度为25 m/s时,面目标回波信号处理结果
5 结论
合成孔径雷达高度计在传统底视雷达高度计的基础上在顺轨向引入了合成孔径技术,从而提高了测量的分辨率和精度。在顺轨向的合成孔径处理中延迟校正是其中的关键技术。
在合成孔径雷达高度计的延迟校正算法中,重要的算法是Raney算法和SAMOSA的算法。然而Raney算法没有考虑到在卫星收发脉冲间隔内目标到雷达的距离变化,也没有校正卫星垂直速度的影响。SAMOSA算法在Raney算法的基础上增加校正了垂直速度引起的多普勒频率偏移,但忽略了卫星水平速度和垂直速度导致的目标到雷达的距离变化。
本文研究了合成孔径雷达高度计的延迟校正算法,研究了在收发脉冲间隔内卫星水平速度和垂直速度引起的目标到雷达的距离变化带来的影响,建立了延迟校正算法的完整模型,最终给出了一个新的延迟校正算法,该算法消除了卫星运动带来的残余误差。最后采用计算机仿真了点目标以及面目标回波信号,采用3种算法对仿真信号进行了处理。处理结果表明,Raney算法和SAMOSA算法存在较大的误差,而本文算法可以得到准确的校正结果。
[1] Jensen J R and Raney R K. Delay/Doppler radar altimeter: better measurement precision[C]. 1998 IEEE International Geoscience and Remote Sensing Symposium Proceedings, Seattle, WA, 1998, 4: 2011-2013.
[2] Raney R K. The delay/Doppler radar altimeter[J]., 1998, 36(5): 1578-1588.
[3] Phalippou L and Enjolras V. Re-tracking of SAR altimeter ocean power-waveforms and related accuracies of the retrieved sea surface height, significant wave height and wind speed[C]. IEEE International Geoscience and Remote Sensing Symposium Proceedings, Barcelona, 2007: 3533-3536.
[4] Raney R K. Resolution and precision of a delay-Doppler radar altimeter[C]. IEEE Proceedings of OCEANS 2005, Washington, 2005, 3: 1989-1993.
[5] Galin N, Wingham D J, Cullen R,. Measuring the pitch of CryoSat-2 using the SAR mode of the SIRAL altimeter [J]., 2014, 11(8): 1399-1403.
[6] Halimi A, Mailhes C, Tourneret J Y,. A semi-analytical model for Delay/Doppler altimetry and its estimation algorithm[J]., 2014, 52(7): 4248-4258.
[7] Jain M, Andersen O B, Dall J,. Sea surface height determination in the Arctic using Cryosat-2 SAR data from primary peak empirical retrackers[J]., 2015, 55(1): 40-50.
[8] Donlon C, Berruti B, Buongiorno A,. The Global Monitoring for Environment and Security (GMES) Sentinel-3 Mission[J]., 2012, 120: 37-57.
[9] Halimi A, Mailhes C, Tourneret J Y,. Including antenna mispointing in a semi-analytical model for Delay/Doppler altimetry[J]., 2015, 53(2): 598-608.
[10] Fenlglio-Marc L, Dinardo S, Scharroo R,.The German Bight: a validation of CryoSat-2 altimeter data in SAR mode[J]., 2015, 55(11): 2641-2656.
[11] Halimi A, Mailhes C, Tourneret J Y,. Exploiting time and frequency information for Delay/Doppler altimetry[C]. Signal Processing Conference (EUSIPCO), Lisbon, 2014: 1088-1092.
[12] Ray C, Martin-Puig C, Clarizia M P,. SAR altimeter backscattered waveform model[J].,2015, 53(2): 911-919.
[13] D,Aria D, Guccione P, Rosich B,. Delay/Doppler altimeter data processing[C]. IEEE International Geoscience and Remote Sensing Symposium, Barcelona, 2007: 137-140.
[14] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 27-30.
Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 27-30.
[15] 杨双宝. 基于合成孔径技术的高精度雷达高度计技术研究[D]. [博士论文], 中国科学院(空间科学与应用研究中心), 2007.
Yang Shuang-bao. Study of heigh precision SAR altimteter technology[D]. [Ph.D. dissertation], Center for Space Science and Applied Research, Chinese Academy of Sciences, 2007.
[16] 杨双宝, 刘和光, 许可. 合成孔径高度计的海面回波仿真[J]. 遥感学报, 2008, 11(4): 446-451.
Yang Shuang-bao, Liu He-guang, and Xu Ke. The simulation of sea surface echo of synthetic aperture radar altimeter[J]., 2008, 11(4): 446-451.
[17] Sun Yi-ping and Sweeting M. Directional wave spectrum estimation by synthetic aperture radar altimeter[C]. IEEE International Geoscience and Remote Sensing Symposium Proceedings, Honolulu, HI, 2000, 5: 2340-2342.
[18] Donelan M A and Pierson W J. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry[J].:, 1987, 92(C5): 4971-5029.
[19] Yang Shuang-bao, Liu He-guang, Xu Ke,. The mean echo model and data process of SAR altimeter[C]. IEEE International Geoscience and Remote Sensing Symposium Proceedings, Vancouver, BC, 2011: 2077-2080.
A New Range Migration Correction Algorithm and Its Simulation for SAR Altimeter
Wang Lei①②③Xu Ke①③Shi Ling-wei①③Yang Shuang-bao①③
①(,,100190,)②(,100049,)③(,,100190,)
The Range Migration Correction (RMC) is a key technique of synthetic aperture radar altimeter which is more precise than the conventional radar altimeter. Because of the satellite motion, the distance change between the satellite and the observed target will bring about some residual errors, but they are ignored in the existing RMC algorithms. In this paper, the influences of the vertical and horizontal velocities of the satellite are studied, then an RMC model is builded, and finally a new RMC algorithm which corrects not only the slant range error but also the residual errors is proposed. The simulation results show that this new algorithm can obtain more accurate outcomes.
SAR altimeter; Range migration algorithm; Residual error
TN953
A
1009-5896(2015)11-2713-06
10.11999/JEIT150282
2015-03-09;改回日期:2015-06-29;
2015-08-24
王磊 wanglei_1208@126.com
王 磊: 男,1986年生,博士生,研究方向为雷达高度计信号处理.
许 可: 男,1967年生,博士,研究员,博士生导师,主要研究方向为星载雷达高度计系统技术、合成孔径雷达高度计系统技术和信号处理技术.
史灵卫: 男,1983年生,博士,主要从事雷达高度计的数据处理技术研究.

