模态依赖不确定时滞Markov跳变系统鲁棒耗散滤波器设计方法

刘俊丽,周敬轩,周秀杰,吴涨波,彭淑罗,李艳辉

(1.东北石油大学电气信息工程学院,黑龙江大庆 163318; 2.北京市昌平区第一中学,北京 102200; 3.上海海洋大学工程学院,上海 201306; 4.中国石油华北油田公司数据中心,河北任丘 062550)

模态依赖不确定时滞Markov跳变系统鲁棒耗散滤波器设计方法

刘俊丽1,周敬轩2,周秀杰1,吴涨波3,彭淑罗4,李艳辉1

(1.东北石油大学电气信息工程学院,黑龙江大庆 163318; 2.北京市昌平区第一中学,北京 102200; 3.上海海洋大学工程学院,上海 201306; 4.中国石油华北油田公司数据中心,河北任丘 062550)

Markov跳变系统描述系统结构随时间变化的规律,使系统性能不受外界因素和内部结构的影响.针对一类模态依赖不确定时滞Markov跳变系统,引入耗散性能,设计相应的鲁棒滤波器.通过时滞依赖Lyapunov函数构造,利用伊藤微分规则和变量替换法,建立滤波误差系统均方随机渐近稳定、且严格鲁棒耗散的充分条件;并利用求解线性矩阵不等式设计滤波器.数值仿真结果验证设计方法的可行性.

Markov跳变系统;鲁棒耗散滤波器;模态依赖;线性矩阵不等式

DOI 10.3969/j.issn.2095-4107.2015.05.014

0　引言

Markov跳变系统是一类随机混杂系统,包含时间演化和事件驱动两种动态机制.一方面,它可以描述实际系统在运行过程中由环境变化、元件失效等引起结构参数发生随机突变的现象,因此受到广泛关注[1-2].文献[3]利用期望的逗留时间,建立系统几乎必然稳定的充分条件.文献[4]结合TP(Transition Probability)特性和矩阵变换法,研究转移概率部分已知的不确定Markov跳变系统的H∞状态反馈控制问题.文献[5]针对离散时间广义非线性Markov跳变系统设计l2-l∞滤波器.文献[6]对具有时延和丢包的网络控制系统建立Markov跳变模型,设计H∞滤波器.另一方面,时滞和不确定性使得系统性能变差[7],因此,有必要对不确定时滞Markov跳变系统进行研究.

耗散性能建立能量函数与供给率之间的关系,在系统稳定性分析和鲁棒控制方面起重要作用[8-10].文献[11]基于T-S(Takagi-Sugeno)模糊模型,讨论具有随机时延的非线性系统模糊耗散滤波器设计方法.文献[12]针对一类具有传感器故障和随机丢包的网络控制系统,设计鲁棒可靠性耗散滤波器.文献[13]考虑凸多面体不确定性,研究中立系统鲁棒耗散滤波问题.近年来,耗散性能研究已经延伸到Markov跳变系统[14-15].然而,现有文献大多研究耗散控制问题,为了进一步完善综合控制问题,研究Markov跳变系统的鲁棒耗散滤波问题具有重要意义.

针对一类模态依赖不确定时滞Markov跳变系统,文中采用矩阵变换方法,实现Lyapunov矩阵和系统矩阵的解耦;运用Jensen不等式和线性矩阵不等式(LMIs)方法,得到保守性较低的滤波器存在的充分条件,保证滤波误差系统均方随机渐近稳定并具有严格耗散性.数值仿真结果表明,设计的滤波器可以较好地跟踪原系统状态,有效地抑制干扰.

1　系统描述及预备知识

考虑不确定时滞Markov跳变系统:

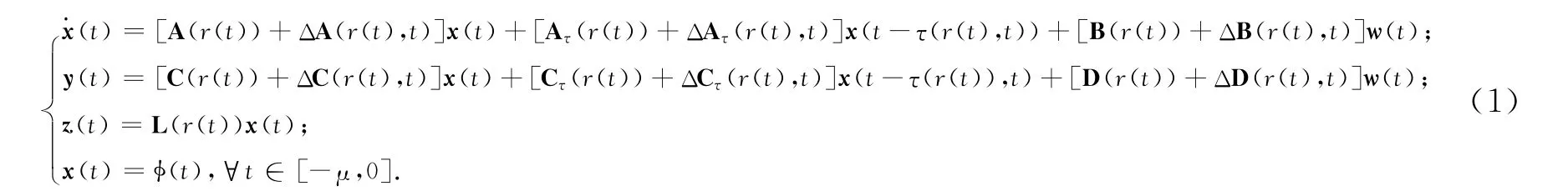
式中:x(t)为系统状态向量,x(t)∈Pn;y(t)为系统测量输出,y(t)∈Pq;z(t)为待估计信号,z(t)∈Pm;w(t)为扰动信号,w(t)∈Pp,且w(t)∈L2[0,∞);{r(t),t≥0}为定义在概率空间{Ω,F,P}上的连续时间Markov链,在有限模态集S={1,2,…N}取值,并且转移概率矩阵Γ=(πij)i,j∈S.在时刻t+Δt从模态i转移到模态j的概率为

当r(t)=i∈S时,记系统矩阵形式为A(r(t))=Ai0,ΔA(r(t),t)=ΔAi(t).其中,τ(r(t),t)为i模态下系统的时变,时延满足0＜τi(t)≤di＜∞,˙τi(t)≤μi＜1,di和μi为实常数,令d=max{di}.系统的不确定参数可表示为

式中:H1i,H2i,E1i,E2i,E3i为适当维数的已知实矩阵,反映系统的不确定性结构;Fi(t)为满足≤I的未知矩阵,且Lebesgue是可测的.

对于跳变系统(1),设计滤波器:

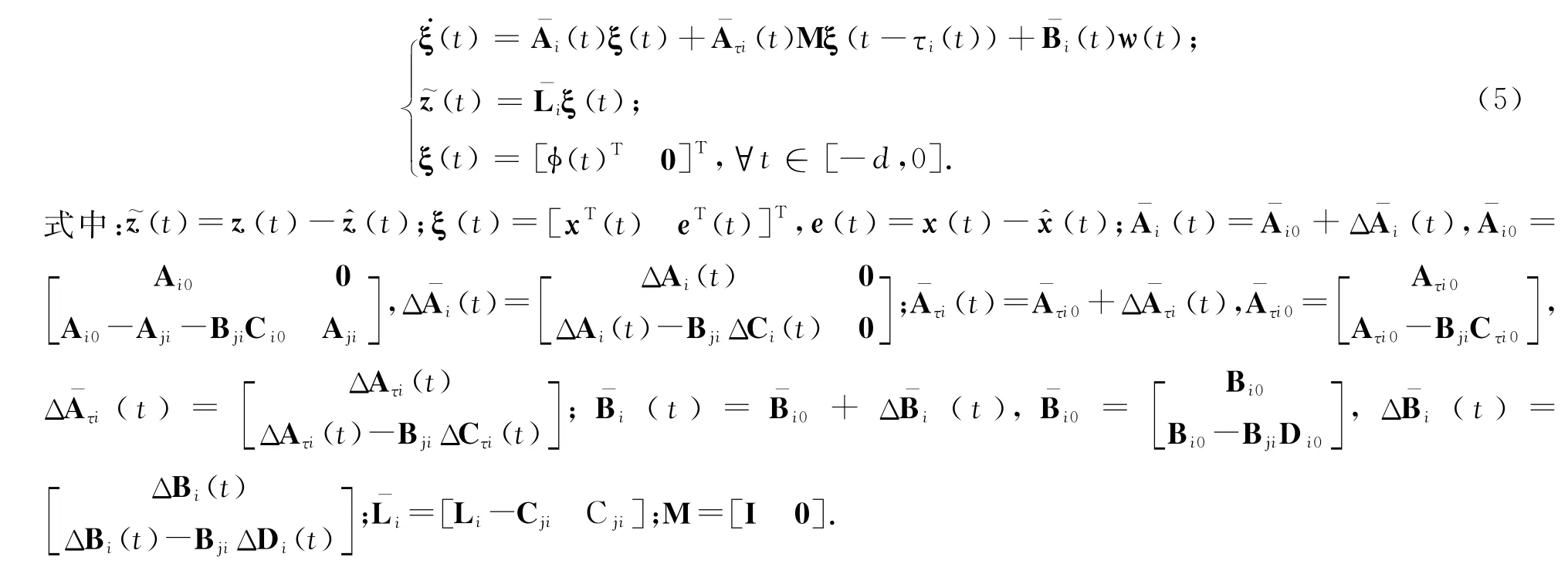
对于滤波误差系统(5),二次能量供给函数定义为

K,S,P表示耗散供给率.鲁棒耗散滤波包含鲁棒H∞滤波(K=-I,S=0,P=γ2I)和鲁棒无源滤波(K=0,S=I,P=0),并在两者之间进行较好的折中,取得保守性较小的结果,更具一般性.为了说明滤波器的鲁棒耗散性能,给出定义:

定义1 滤波误差系统(5)是严格鲁棒(K,S,P)耗散的,如果对于任意的T1＞0和所有非零的w(t)∈ L2[0,∞),在零初始条件下,存在常数α＞0,不等式成立.不失一般性,假设K＜0.

文中目标是确定滤波器参数Afi,Bfi,Cfi,使得滤波器(4)为跳变系统(1)的鲁棒耗散滤波器.

2　鲁棒耗散滤波器设计

定理1 给定矩阵S和对称矩阵K,P,滤波误差系统(5)鲁棒耗散问题有解的充分条件:存在正定对称矩阵Pi∈P2n×2n,Q1∈P2n×2n,Q2∈P2n×2n,Q3∈P2n×2n,使不等式成立:

证明 选取Lyapunov函数:

根据伊藤微分规则,得到系统的无穷小算子:

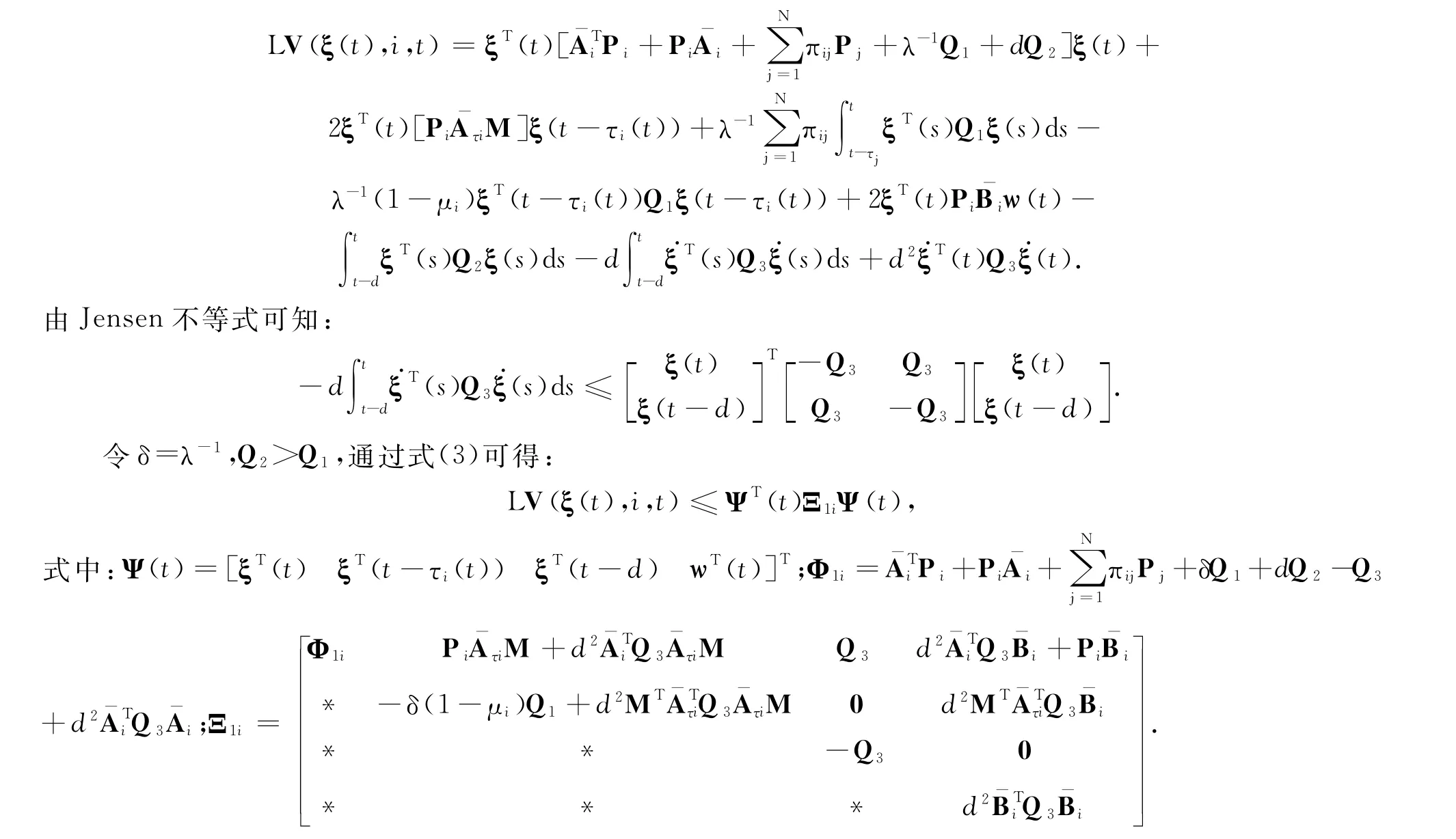
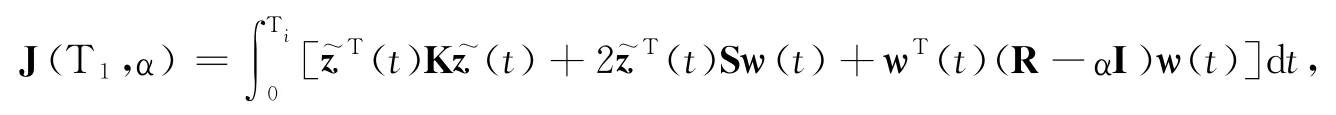
得:

式中:

定理1给出鲁棒耗散滤波器存在的时滞依赖充分条件,与时滞无关相比,具有较小的保守性.文中推导时应用Jensen不等式处理积分项,减少计算量.

定理2 给定矩阵S和对称矩阵K,P,对于系统容许的不确定性,存在鲁棒耗散滤波器(4),当且仅当存在常数εi＞0和正定对称矩阵以及矩阵Wi,Zi,Cfi时,使式(7)和式(8)成立.

证明 利用文献[9]引理1,并结合Schur补性质可知式(6)等价于:

定义一组新的变量:Wi=YiAfi,Zi=YiBfi,代入不等式(11)可得式(8)成立,滤波器参数见式(9),定理得证.

当s={1}时,系统只有一个模态,系统(1)转变为普通的线性系统.

3　仿真分析

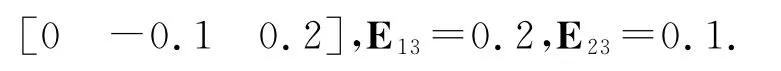
关于城阳区乡村旅游者喜欢的旅游项目，抽样调查结果显示，大多数旅游者喜欢采摘、划船、农业观光、农业种植、登山等体验型乡村旅游产品。棋牌类传统乡村旅游产品受欢迎程度不高，可见乡村旅游者的需求在发生改变，而探险类新型旅游产品受欢迎程度较低，本文认为大多数旅游者还是非常注重乡村旅游的安全性。

在初始条件x(0)=[1 1 1]T和干扰输入w(t)=e-0.4tsin(πt)时,跳变系统的模态r(t)和干扰输入见图1,滤波误差曲线见图2,系统状态x和滤波器估计的状态xf曲线见图3.

由图(1-3)可知,在干扰作用下,考虑给定的耗散供给率,滤波估计状态能够很好地跟踪系统状态,滤波误差曲线也能很快趋于稳定,说明系统具有较好的性能,证明文中方法的有效性.

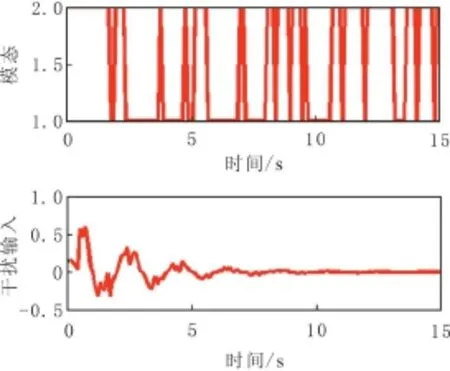
图1　跳变系统模态和干扰曲线Fig.1 Modal and interference curve

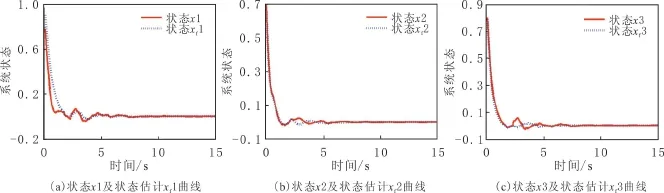
图3　跳变系统状态和滤波器估计状态曲线Fig.3 System status and filter curves to estimate the state

4　结论

(1)根据Lyapunov稳定性理论,建立不确定时变时滞Markov跳变系统滤波器存在的充分条件,在所容许的不确定性和能量有界的外界干扰下,使滤波误差系统均方随机渐近稳定并满足期望的耗散性能指标.

(2)考虑参数的不确定性,利用Schur补引理和全等变换法,提出LMIs形式的鲁棒耗散滤波器设计方法.

(3)文中设计的滤波器对于干扰具有较强的鲁棒性.

[1] Shi Peng,Yin Yanyan,Liu Fei,et al.Robust control on saturated Markov jump linear systems with missing information[J].Information Sciences,2014,265:123-138.

[2] 刘飞.不确定跳变系统鲁棒滤波[J].控制与决策,2005,20(1):32-35. Liu Fei.Robust filtering for uncertain jump systems[J].Control and Decision,2005,20(1):32-35.

[3] Song Yang,Dong Hao,Yang Taicheng,et al.Almost sure stability of discrete-time Markov jump linear systems[J].IET Control Theory and Applications,2014,8(11):901-906.

[4] Shen Mouquan,Zhang Guangming,Yuan Yuhao,et al.Relaxedcontroller design for continuous Markov jump system with incomplete transition probabilities[J].Circuits Systems and Signal Process,2014,33(5):1393-1410.

[5] Li Lin,Zhong Lei.Generalised nonlinearfiltering of discrete-time Markov jump descriptor systems[J].International Journal of Control,2014,87(3):653-664.

[6] 张皓,严怀成,刘涛,等.一类丢包时延网络控制系统的鲁棒滤波[J].控制与决策,2009,24(12):1865-1868. Zhang Hao,Yan Huaicheng,Liu Tao,et al.Robust H∞filtering for networked control systems with data packet dropout and delays [J].Control Theory and Applications,2009,24(12):1865-1868.

[7] 段玉波,张会珍,赵万春,等.基于状态观测器的线性不确定多时滞系统的鲁棒控制[J].大庆石油学院学报,2004,28(5):58-64. Duan Yubo,Zhang Huizhen,Zhao Wanchun,et al.Observer-based robust control for uncertain linear systems with multi-time delays [J].Journal of Daqing Petroleum Institute,2004,28(5):58-64.

[8] 李彦江,段广仁.T-S模糊系统的鲁棒耗散控制[J].系统工程与电子技术,2007,29(9):1518-1523. Li Yanjiang,Duan Guangren.Robust dissipative control for T-S fuzzy systems[J].Systems Engineering and Electronics,2007,29 (9):1518-1523.

[9] 马跃超,程东东,赵宇霞,等.不确定时滞离散非线性系统的鲁棒耗散滤波[J].控制工程,2012,19(2):229-231. Ma Yuechao,Cheng Dongdong,Zhao Yuxia,et al.Robust dissipative filter for a class of discrete time-delay nonlinear systems with parameter uncertainties[J].Control Engineering of China,2012,19(2):229-231.

[10] 邵克勇,于显利,任志强.基于全面供给率的时滞系统状态反馈控制器设计[J].大庆石油学院学报,2006,30(6):86-89. Shao Keyong,Yu Xianli,Ren Zhiqiang.Controller design of a time-delay system state feedback based on the full supply rate[J]. Journal of Daqing Petroleum Institute,2006,30(6):86-89.

[11] Lin Qiongbin,Wang Wu,Yang Fuwen,et al.Fuzzy dissipative filtering for nonlinear systems with stochastic delay[J].Systems Engineering and Electronics,2009,31(10):2434-2439.

[12] Mathiyalagan Kalidass,Park Ju H,Sakthivel Rathinasamy.Robust reliable dissipative filtering for networked control systems with sensor failure[J].IET Signal Processing,2014,8(8):809-822.

[13] Duan Guangren,Lu Lingling,Wu Aiguo.Robust dissipative filtering for continuous-time polytopic uncertain neutral systems[J]. Journal of Systems Engineering and Electronics,2009,20(3):598-606.

[14] Sheng Li,Gao Ming,Zhang Weihai.Dissipative control for Markov jump non-linear stochastic systems based on T-S fuzzy model [J].International Journal of Systems Science,2014,45(5):1213-1224.

[15] Wang Guoliang,Zhang Qingling,Yang Chunyu.Dissipative control for singular Markovian jump systems with time delay[J].Optimal Control Applications and Methods,2012,33(4):415-432.

TP273

A

2095-4107(2015)05-0112-07

2015-07-10;编辑:张兆虹

空间智能控制技术国家级重点实验室开放基金项目(002008834000);黑龙江省博士后科学研究发展基金项目(LBHQ13177);黑龙江省自然科学基金项目(F201403);东北石油大学校内培育基金项目(XN2014112);东北石油大学研究生创新科研项目(YJSCX2014-029NEPU)

刘俊丽(1991-),女,硕士研究生,主要从事鲁棒控制、滤波和智能控制方面的研究.

周敬轩,E-mail:zhoujingxuan-cp@163.com