斜拉桥上无缝线路纵向相互作用理论及试验研究

魏贤奎,周 颖,刘 浩,王 平

(1.川南城际铁路有限责任公司,四川自贡 643000；2.成都铁路局, 成都 610031；3.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

斜拉桥上无缝线路纵向相互作用理论及试验研究

魏贤奎1,周 颖2,刘 浩3,王 平3

(1.川南城际铁路有限责任公司,四川自贡 643000；2.成都铁路局, 成都 610031；3.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

运用梁轨纵向相互作用机理,建立斜拉桥上无缝线路纵向力计算模型,以一座铁路常用双塔钢桁斜拉桥为例,对斜拉桥上无缝线路纵向相互作用规律进行理论和试验研究。分析结果表明：在主桥左右两端各铺设一组单向伸缩调节器,主桥上钢轨纵向力可得到有效的控制,现场试验测试的桥面纵向位移及钢轨伸缩力分布规律与理论计算基本相同,所建立模型可用于斜拉桥上无缝线路纵向相互作用分析；钢轨挠曲力计算时,可在斜拉桥主跨及其邻跨上布置荷载,且不必考虑列车入桥方向的变化；钢轨伸缩调节器可有效减弱列车制动荷载下的梁轨相互约束作用,减小线路受力变形。

斜拉桥；纵向相互作用；无缝线路；钢轨伸缩调节器；试验研究

1 概述

斜拉桥作为一种拉索体系，较普通梁式桥的跨越能力要大，是大跨度铁路桥梁的主要桥型。因其结构特殊，跨越能力强，施工难度低等优点，近年来，被广泛的应用于跨越峡谷、河流、高速公路、铁路等地区[1-2]。由于桥梁结构的特殊性，使得温度、列车及制动荷载作用下的线路间纵向相互作用规律与普通桥梁不同，目前，国内外学者对大跨斜拉桥上梁轨纵向相互作用规律有了一定的研究[3-6]，但仅针对桥上铺设无缝线路时，实际上，在大跨度桥上铺设无缝线路，桥梁伸缩引起的梁轨相互作用加剧，钢轨将承受巨大的附加力，超出钢轨的允许应力，同时桥梁和钢轨也将产生较大的相对位移影响线路的稳定性，因此对于大跨度桥上无缝线路有必要设置钢轨伸缩调节器。

本文以某新建铁路钢桁斜拉桥为背景，建立计算模型，分析了铺设钢轨伸缩调节器后梁轨纵向相互作用规律，另外，为了验证理论模型的可行性，针对该桥梁特进行了现场相关试验研究。

2 纵向约束作用计算模型及参数

2.1 计算模型

梁轨纵向相互作用机理是分析桥上无缝线路纵向力产生的基础，以铁路上常用的下承式斜拉桥为例，图1中的计算模型示意了典型的下承式斜拉桥上无缝线路的梁轨相互作用关系，系统结构特点如下：钢轨通过线路阻力与主梁下缘相互作用；主梁上缘与主塔墩通过斜拉索相互作用。

图1 斜拉桥梁轨纵向约束作用计算模型

不同计算工况下，线路纵向阻力作用于钢轨上时引起钢轨附加力，线路纵向阻力作用于主梁上时，通过斜拉索或纵向阻尼装置将力传至主塔墩上，引起主塔墩产生力和位移，钢轨、主梁、斜拉索及主塔墩是一相互作用的耦合系统，通过求解该系统的平衡位置，即可求得各部分的力和位移分布情况。以某新建铁路双线钢桁斜拉桥为例，线路设计荷载为中-活载。主桥采用(36+96+228+96+36) m半漂浮体系钢桁梁斜拉桥；主桥左、右侧为5 跨32 m简支梁，计算模型[7-8]见图1。

计算模型中，对于带纵梁及制动撑架的钢桁架梁，纵梁可视为普通梁的上翼缘，梁轨相对位移即是纵梁与钢轨间的相对位移，制动撑架可视为纵向弹簧，在不考虑下弦杆轴向压缩的情况下，可将该弹簧视为与固定支座所在墩(简化为纵向弹簧)串联。钢轨与路基的连接，梁与钢轨的连接均采用弹簧单元模拟，对不同的部分采用不同的单元参数[9-10]。

2.2 设计参数

轨道采用60 kg/m钢轨；有砟碎石道床，Ⅲa型混凝土枕，每千米铺设1 667根；根据中铁二院提供相关资料，桥位最高轨温59.2 ℃，最低轨温-3.3 ℃，设计锁定轨温为36±5 ℃，钢轨升温幅度为28.2 ℃，降温幅度为44.3 ℃，简支梁体升温幅度为15 ℃，钢桁梁体升温幅度为25 ℃。梁体截面为矩形，简支梁截面积8 m2，钢桁梁换算截面积为1.734 m2，混凝土梁的弹性模量为3.55×1010N/m2，线膨胀系数为1.0×10-5/℃，钢桁梁的弹性模量为2.06×1011N/m2，线膨胀系数为1.18×10-5/℃。主塔的横截面惯性矩为167.4 m4，横截面面积为30.8 m2，横截面高度为7.0 m；斜拉索弹性模量为1.9×1011N/m2，线膨胀系数为1.1×10-5/℃。

3 纵向约束作用研究

3.1 桥上无缝线路参数测试

对于桥上无缝线路，梁因温度变化而产生伸缩，在列车荷载作用下梁因挠曲而产生位移，在明桥面上，梁上翼缘的这种纵向变形(即伸缩和位移)，将通过梁、轨间的联结约束，使钢轨受到纵向力的作用。对于有砟桥而言，道床也会对梁、轨间的相对位移产生一定的约束阻力，因无缝线路设计要求扣件阻力大于道床阻力，梁轨间的约束阻力即为道床阻力，根据《铁路无缝线路设计规范》之规定[11]，道床阻力可采用常阻力和非线性阻力两种型式。为了明确梁轨间纵向约束阻力，特对文中所述斜拉桥上有砟道床纵向阻力进行了现场测试，选取4组典型测试结果，如图2所示。

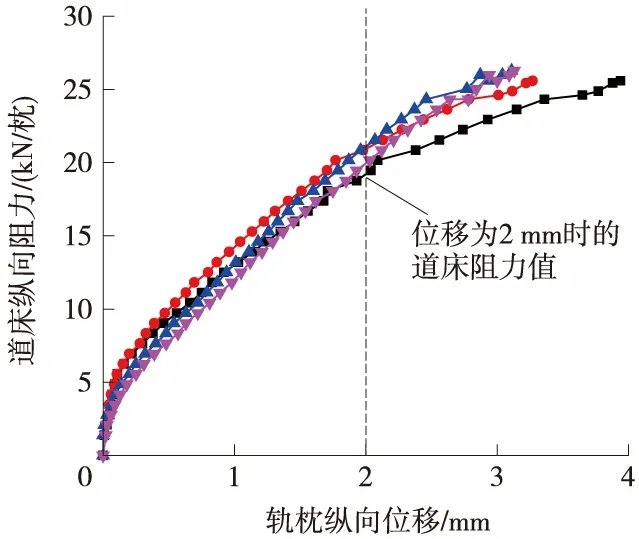
图2 道床纵向阻力

通过测试结果得，当轨枕纵向位移为2 mm时，道床纵向阻力值约为18.7 kN/枕，与《铁路无缝线路规范》规定的18 kN/枕几乎相同，道床纵向阻力测试结果具有一定离散性，但整体规律一致，可认为轨枕在位移2 mm后出现滑移现象。由于测试时间和线路条件的限制，并没有对道床纵向阻力值进行大量测试并回归分析拟合得到道床阻力-位移关系曲线，但从测试结果可以看出，取极限位移为2 mm时，道床阻力值与规范规定的相差不大，因此，在进行梁轨纵向相互作用分析时，线路纵向阻力根据《铁路无缝线路规范》之规定：线路阻力形式为双线性，无载取为15 kN/m/轨，有载取为24 kN/m/轨，极限位移均为2 mm。另外，通过室内试验，钢轨伸缩调节器用小阻力扣件阻力值约为8 kN/m/轨，极限位移为0.5 mm。

3.2 钢轨伸缩附加力分析

由于算例钢桁斜拉桥温度跨度较大，可能导致钢轨伸缩附加力过大，从而引起轨道强度和稳定性问题，这就需要铺设钢轨伸缩调节器和铺设小阻力扣件来避免该问题[12]。但是，当温度跨度很大时，即使全桥铺设小阻力扣件也不能满足钢轨强度和稳定性要求，因此，在进行钢轨伸缩附加力分析时，分为两种典型计算工况：工况1，全桥铺设无缝线路；工况2：在主桥左右两端各铺设一组单向伸缩调节器，尖轨放在主桥上，如图3所示。钢轨伸缩附加力及桥面纵向位移计算结果见图4。

图3 钢轨伸缩调节器布置示意

图4 伸缩工况计算结果

由图4可以看出：工况1钢轨最大压力为1 469.4 kN(189.7 MPa)，梁轨相对位移最大值为37.5 mm；工况钢轨最大压力为554.3 kN，梁轨相对位移最大值为5.29 mm。由图4(a)可知，铺设钢轨伸缩调节器之后，钢轨伸缩力大幅降低，尤其是斜拉桥梁缝处，主桥上钢轨纵向力也得到有效的控制。由于钢轨伸缩调节器可以明显减弱梁轨间纵向约束作用，在温度力作用下，伸缩区钢轨几乎处于自由状态，主梁左右端梁缝附近一定范围内的伸缩力完全放散掉，并且主梁范围内的钢轨纵向力也相对较小。

3.3 梁轨纵向约束试验研究

上文对伸缩工况下的钢轨受力和变形进行了理论分析，为验证模型对分析斜拉桥上无缝线路纵向约束作用的可行性，对钢轨伸缩力、桥面纵向位移等进行了现场测试。

3.3.1 钢轨温度力测试

采用TS-5钢轨温度应变仪对钢轨温度力进行测试，分别在斜拉桥左侧两跨、主桥跨以及左侧一跨简支梁范围内布置测点，现场钢轨温度力测试如图5所示。

图5 钢轨温度力测试

(1)对于路基上无缝线路，假设两次测试的钢轨温度分别为T1、T2，仪器的度数相应为ε1、ε2，则钢轨伸缩可以采用下式计算

(1)

其中，δ=ε2-ε1；ΔT=T2-T1；A为钢轨截面面积；E为钢轨的弹性模量；α为钢轨线膨胀系数。因路基上钢轨应变δ=0，则钢轨伸缩力Pt=-2.48ΔT，以钢轨受拉为正。

(2)对于桥上无缝线路，钢轨伸缩力仍采用式(1)计算，其中δ为桥梁伸缩引起的钢轨附加应变，规定钢轨伸长应变为正。

(3)当桥上铺设钢轨伸缩调节器时，设扣件阻力所能提供的阻力为F，则测点处钢轨应力为

(2)

此时，钢轨应变由两部分组成，即钢轨本身温度变化和扣件阻力的约束作用，此时钢轨应变为

(3)

钢轨应力为

(4)

则钢轨伸缩力为

综上可得，对现场测试的钢轨伸缩力可通过式(1)进行计算，以钢轨升温、伸长应变、受拉为正。

通过对测试结果进行计算整理可得钢轨伸缩力分布如图6所示，取斜拉桥左端梁缝处为坐标原点。

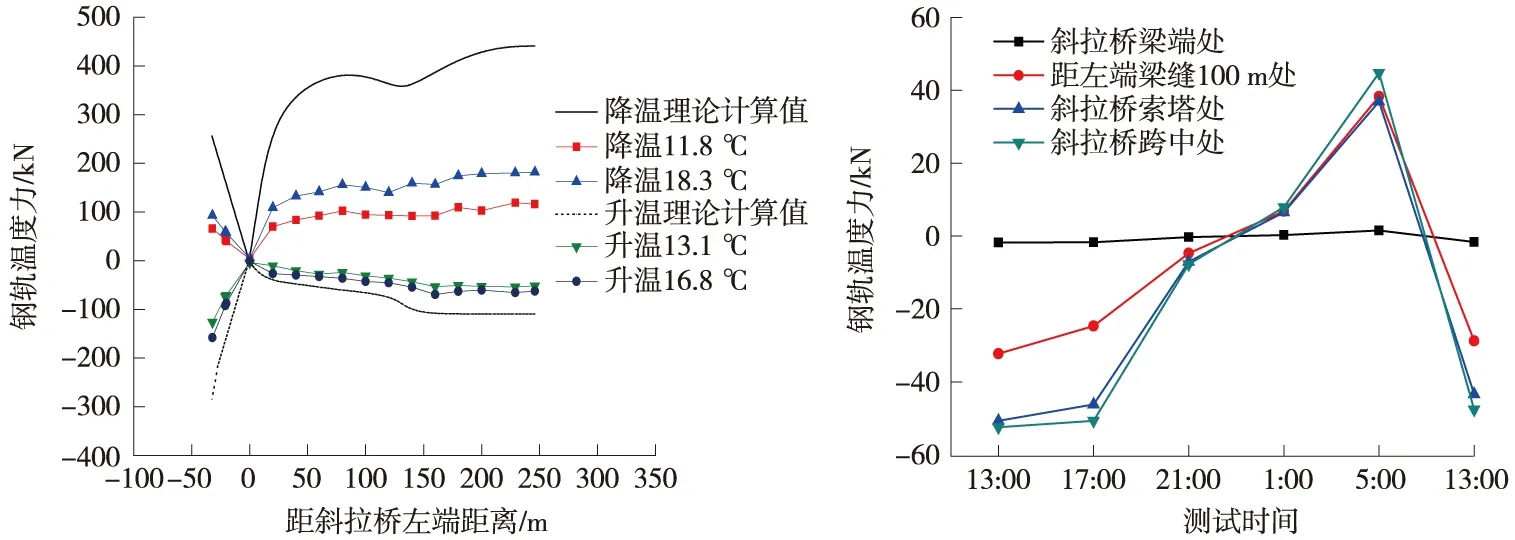
图6 钢轨温度力曲线

由测试结果可以看出，由于斜拉桥梁端位置处设置钢轨伸缩调节器，此处钢轨伸缩力值很小，由梁端向跨中方向，伸缩力呈逐渐增大的趋势。通过与理论计算所得的结果进行对比分析可得，现场测试的钢轨伸缩力分布规律及其大小与理论计算值基本相同。

3.3.2 桥面纵向位移测试

梁轨相对位移测试时，利用道砟挡砟墙，用细长线连接挡砟墙上的标定点，形成基线，与钢轨上粘贴的标尺进行对应读数，即可得到梁轨相对位移值。现场测试见图7。

图7 梁轨相对位移现场测试

选取半跨斜拉桥及左侧一跨简支梁进行梁轨相对位移测试，共测试1个昼夜(24 h)，测试结果见图8，取斜拉桥左端梁缝处为坐标原点。

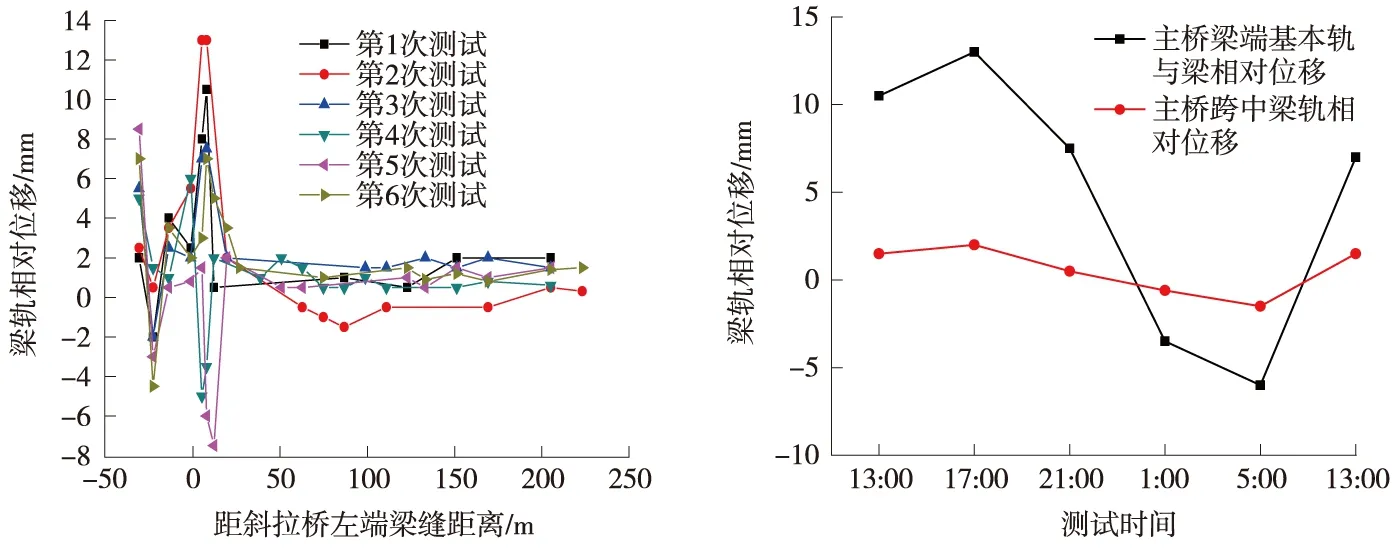
图8 梁轨相对位移测试曲线

由测试结果分析得，斜拉桥梁端处梁轨相对位移较大，跨中位置附近处很小。通过与前文理论计算比较可得，理论计算所得的梁轨相对位移分布规律与现场实际测试结果相同。

由于桥梁高度等原因，不能测出斜拉桥在温度循环荷载下的绝对伸长量，因此测量选择靠近简支梁固定支座一侧的斜拉桥梁端测试相对伸缩位移。将长钢尺一端固定在简支梁梁端，另一端自由地放置在斜拉桥上，从而通过读数确定梁端的伸缩量。测量时应该避免阳光直射钢尺。测试时大气、钢轨温度及斜拉桥梁端伸缩位移见表1。

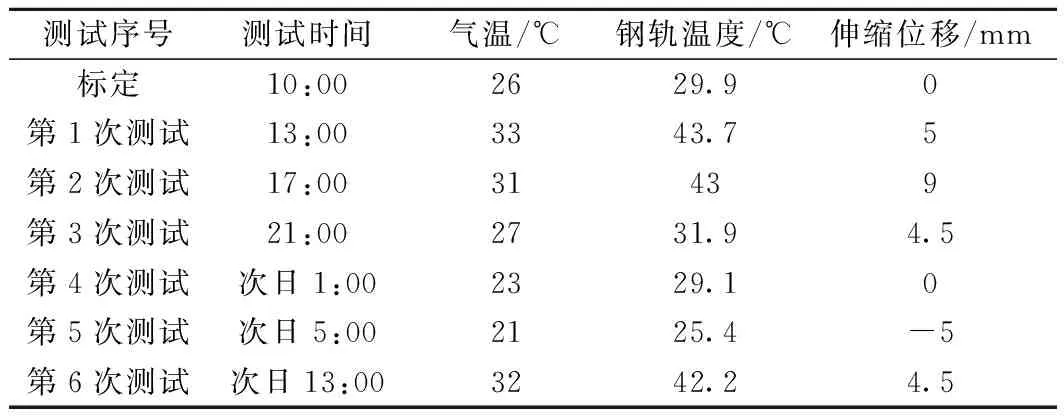
表1 大气、钢轨温度及桥梁伸缩位移

由以上试验结果可知，理论分析所得的钢轨受力和变形规律与试验基本相同，因此，所建立的斜拉桥上无缝线路纵向力分析模型是可行的。

3.4 钢轨挠曲附加力分析

由于斜拉桥主跨跨度较大，主跨上布置满荷载时主梁的变形会较大，进而引起钢轨内产生较大的挠曲附加力，因此，在进行挠曲工况计算时，假设荷载类型为中-活载，左侧入桥，作用梁跨为(36+96+228) m。与伸缩工况相同，分为工况1、2两种典型计算工况。计算结果见图9。

图9 挠曲工况计算结果

由计算结果可于看出，工况1和工况2计算所得的钢轨挠曲附加力最大值差别较小，另外，主跨范围内钢轨和梁体纵向位移相差也不大。这主要是由于钢轨伸缩调节器布置在梁端位置，而斜拉桥主桥跨度较大，主跨处于线路固定区，当挠曲荷载主跨满载时，较大的梁体变形使得钢轨在道床纵向阻力的约束下产生较大的纵向力。对于桥上无缝线路，钢轨挠曲力一般不会成为线路强度和稳定性的控制因素，但是对于大跨钢桁梁桥，挠曲荷载可能会引起较大的主梁变形，进而产生较大的墩台纵向力，因此，建议此类桥型按主跨满载的布置方式计算钢轨挠曲附加力和检算桥梁墩台。

3.5 钢轨制动附加力分析

算例斜拉桥采用半漂浮体系，主梁在顺桥向不设置纵向约束，仅通过斜拉索间接与主塔墩相连，此种体系下为了减小列车制动作用下的结构变形，制动附加力计算时采用以下2种工况：工况1，未铺设钢轨伸缩调节器；工况2，在主桥左右两端各铺设一组单向伸缩调节器。假设荷载类型为中-活载，列车左侧入桥，作用跨度为(36+96+228+96+36) m；钢轨制动附加力、桥面纵向位移计算结果如图10所示。

图10 制动工况计算结果

由以上计算结果可知，工况1钢轨最大制动附加力为279.8 kN，钢轨纵向位移最大值为12.5 mm，而设置钢轨伸缩调节器后，钢轨制动附加力、钢轨纵向位移及桥梁纵向位移得到大幅度的降低，这主要是因为桥梁与钢轨间的纵向约束作用减弱，大部分列车制动荷载直接传递至桥面，使得主梁和钢轨同时几乎同时产生纵向移动，进而线路受力变形得极大改善，这也说明大跨度斜拉桥设置钢轨伸缩调节器的必要性。

4 结语

(1)该斜拉桥上道床纵向阻力测试结果整体规律一致，可认为轨枕在位移2 mm后出现滑移现象，道床纵向阻力值约为18.7 kN/枕。

(2)钢轨伸缩调节器使斜拉桥梁缝处钢轨伸缩力大幅降低，主桥上钢轨纵向力也得到有效控制；现场试验分析验证了所建立的斜拉桥上无缝线路纵向约束作用分析模型的正确性，对于铁路钢桁斜拉桥上无缝线路可采用文中所建立的模型进行相关理论分析。

(3)当斜拉桥主跨上布置满荷载时，即使铺设钢轨伸缩调节器，主跨范围内钢轨挠曲力仍然较大，建议此类桥型可在主跨及其邻跨上布置荷载来计算钢轨挠曲力。

(4)铺设钢轨伸缩调节器可明显减弱梁轨纵向约束作用，并有效降低列车制动作用下的钢轨纵向力，进而改善线路受力变形。

[1]金立新，郭慧乾.多塔斜拉桥发展综述[J].公路，2010(7):24-29.

[2]陈忆前.超大跨径斜拉桥的结构体系[D].上海:同济大学，2006.

[3]Freire S， Negrao O， Lopesb V. Geometrical nonlinearities on the static analysis of highly flexible steel cable-stayed bridges[J]. Computers & Structures， 2006，31-32(84):2128-2140.

[4]王平.铁路斜拉桥上无缝线路纵向力规律分析[J].交通运输工程学报，2012(2):4-7.

[5]闫斌，戴公连.高速铁路斜拉桥上无缝线路纵向力研究[J].铁道学报，2012，34(3):83-87.

[6]Daniell W E， Macdonald G J. Improved finite element modeling of a cable-stayed bridge through systematic manual tuning[J]. Engineering Structures， 2007，29(3):358-371.

[7]刘浩.大跨度斜拉桥上无缝线路计算软件开发及应用[J].铁道标准设计，2013(11):9-14.

[8]赵卫华，王平，曹洋.大跨钢桁斜拉桥上无缝线路制动力的计算[J].西南交通大学学报，2012，47(3):361-366.

[9]赵卫华.斜拉桥上无缝线路设计计算方法研究[D].成都:西南交通大学，2010.

[10]闫斌，戴公连，董林育.客运专线斜拉桥梁轨相互作用设计参数[J].交通运输工程学报，2012，12(1):31-37.

[11]中华人民共和国铁道部.TB10015—2012铁路无缝线路设计规范[S].北京：中国铁道出版社，2013.

[12]王斌.钢轨伸缩调节器结构与布置研究[D].成都:西南交通大学，2011.

Theoretical and Experimental Study on Longitudinal Interaction of CWR on Railway Cable-stayed Bridge

WEI Xian-kui1, ZHOU Ying2, LIU Hao3, WANG Ping3

(1.Chuannan Inter-city Railway Co., Ltd., Zigong Sichuan, 643000, China; 2.Chengdu Railway Bureau,Chengdu 610031, China; 3.MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The calculation model of longitudinal force of CWR (continuous welded rail) on cable-stayed bridge is established on the basis of the mechanism of longitudinal interaction. With reference to a double-towers steel truss cable-stayed bridge commonly used in the railway, the longitudinal interaction of CWR and the related experiments are studied. Analysis results show that when the rail expansion device is placed on each side of the main bridge, rail longitudinal force can be effectively controlled, and the distribution of the line longitudinal displacement and the rail expansion are basically the same after theoretical calculation, and the calculation model can be used to analyze longitudinal restraint interaction of CWR on cable-stayed bridge. Rail bending forces are calculated with load on the main span and its adjacent spans in independence of the direction of the train. The rail expansion device effectively weakens the longitudinal restraint interaction between the beam and the rail under the load of train braking, and minimizes track deformation.

Cable-stayed bridge; Longitudinal interaction; Continuous welded rail; Rail expansion device; Experimental study

2014-11-18

国家自然科学基金委高铁联合基金(U1334203)；中央高校基本科研业务(SWJTU12CX079)

魏贤奎(1986—)，男，工程师，博士，E-mail:wei_xiankui@qq.com。

1004-2954(2015)08-0062-06

U213.9

A

10.13238/j.issn.1004-2954.2015.08.015