桥墩温度梯度对高墩大跨桥上无砟轨道影响研究

罗华朋,邢 俊,杨 凯,王 平

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

桥墩温度梯度对高墩大跨桥上无砟轨道影响研究

罗华朋,邢 俊,杨 凯,王 平

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

由于太阳光的辐射,桥墩的向阳和背阳侧就会存在温差,当桥墩高度较大时,墩顶就会产生较大的纵横向位移,带动梁体、轨道板、钢轨偏移,产生桥上无缝线路附加力。为了研究桥墩纵向温度梯度作用下对无砟轨道中轨道部件的受力和变形的影响,基于梁轨相互作用原理,利用有限元方法,建立线-桥-墩一体化模型,计算结果表明：仅考虑桥墩纵向温度梯度荷载时钢轨会产生较大的附加力,且随着桥墩刚度的增加,钢轨附加力也会增加。当同时考虑梁体升温和纵向温度梯度时产生的钢轨附加力小于两者单独作用产生的附加力。无论是仅考虑桥墩纵向温度梯度,还是同时考虑梁体温升和温度梯度,凸台受力和树脂变形均不会发生较大变化。

高墩大跨连续刚构；温度梯度；无缝线路；树脂变形

近年来，由于无缝线路的发展以及铁路基础建设的需要，大量跨越交通干线、陡峭峡谷、宽广河流等特殊领域的高墩大跨桥梁相继出现。由于这些桥梁自身结构的特殊性以及受到自然的影响，使得高墩大跨桥梁无缝线路的设计更加复杂。对于高大桥墩受到温度梯度荷载下，有砟无缝线路的受力和变形作用已经做了大量的研究[1-3]，其中文献[4]分析了桥墩温差荷载作用下桥上无缝线路钢轨附加力大小，但其分析的是简支梁桥属于静定结构，与桥墩刚度无关，对于连续刚构桥梁时桥墩刚度对温度梯度作用下的墩顶位移有密切关系。而且对于桥上铺设无砟轨道时这方面的研究还较少，桥上铺设CRTS系列无砟轨道时，使得梁轨相互作用机理、计算模型及设计参数与传统的有砟轨道又有明显不同，且无砟轨道无缝线路不仅需要检算钢轨强度，还需要综合考虑无砟轨道中梁轨相对位移，以及凸台树脂的受力、变形是否超限。因此，基于上面所述特点，针对高墩大跨连续刚构桥，在桥墩受温度梯度荷载作用下分析了轨道各部件的受力、变形规律。

1 计算方法

1.1 计算原理

与普通桥上无缝线路的伸缩、挠曲、制动、断轨附加力的计算类似，桥墩温度梯度荷载引起的桥上无缝线路纵向附加力同样根据梁轨相互作用原理来分析计算。在温度梯度荷载作用下，墩顶将产生纵横向偏转，且通过固定支座带动梁体一起移动，通过底座板、CA砂浆层、轨道板、扣件系统对钢轨施加纵向力。钢轨受力变形后，对桥面系作用大小相等、方向相反的反作用力，通过梁、支座传递至墩台，梁轨之间形成一个相互作用的力学平衡体系。

1.2 计算模型

以CRTSⅠ型板式无砟轨道为研究对象，无砟轨道结构主要由钢轨、扣件、轨道板、砂浆充填层、底座板、凸形挡台、树脂填充层等结构组成[5]。依据梁轨相互作用原理，建立用于分析桥墩温度梯度的线—桥—墩一体化模型。钢轨、轨道板选用梁单元模拟，根据钢轨、轨道板的截面积、惯性矩以及扭转弯矩等参数，按实际截面属性建模；线路中采用小阻力扣件系统，纵向上采用非线性弹簧单元模拟[6]，横向上采用线性弹簧模拟，竖向刚度为3.0×10-4kN/m，CA砂浆层、树脂层采用非弹性弹簧单元模拟，CA砂浆层考虑了纵向阻力和垂向刚度，整体式单元板摩阻力取为6.3 kN/m，极限位移取为0.2 mm。凸台树脂仅考虑其抗压阻力[7]，树脂强度取线性刚度为80 kN/mm。对于桥梁结构，考虑到梁体、桥墩控制截面的渐变，同时采用能施加温度梯度荷载的beam188梁单元模拟。

以连续刚构桥梁为基本对象，在连续梁两端各布置5跨32 m简支梁，即5×32 m+(89+189+89) m+5×32 m连续刚构桥梁，连续刚构桥的两桥墩高度分别为98、69 m。另外为了消除边界效应，在左右桥台外侧分别建立150 m的路基段。线-桥-墩一体化模型和轨道部件的传力特征如图1所示。

图1 线-桥-墩一体化模型

2 仅考虑梁体及轨道板升温条件下轨道各部件的受力、变形分析

计算无砟轨道桥上无缝线路钢轨伸缩力时，根据我国《铁路无缝线路设计规范》，桥梁梁体和轨道板的温度荷载为Δt=30 ℃。计算得钢轨伸缩附加力、梁轨相对位移、凸形挡台树脂压缩量、凸形挡台纵向力，如图2所示。各部件纵向力和变形最大值见表1。图中树脂变形正值表示离缝，负值表示压缩。

表1 梁体、轨道板同时升温条件下轨道各部件受力和变形

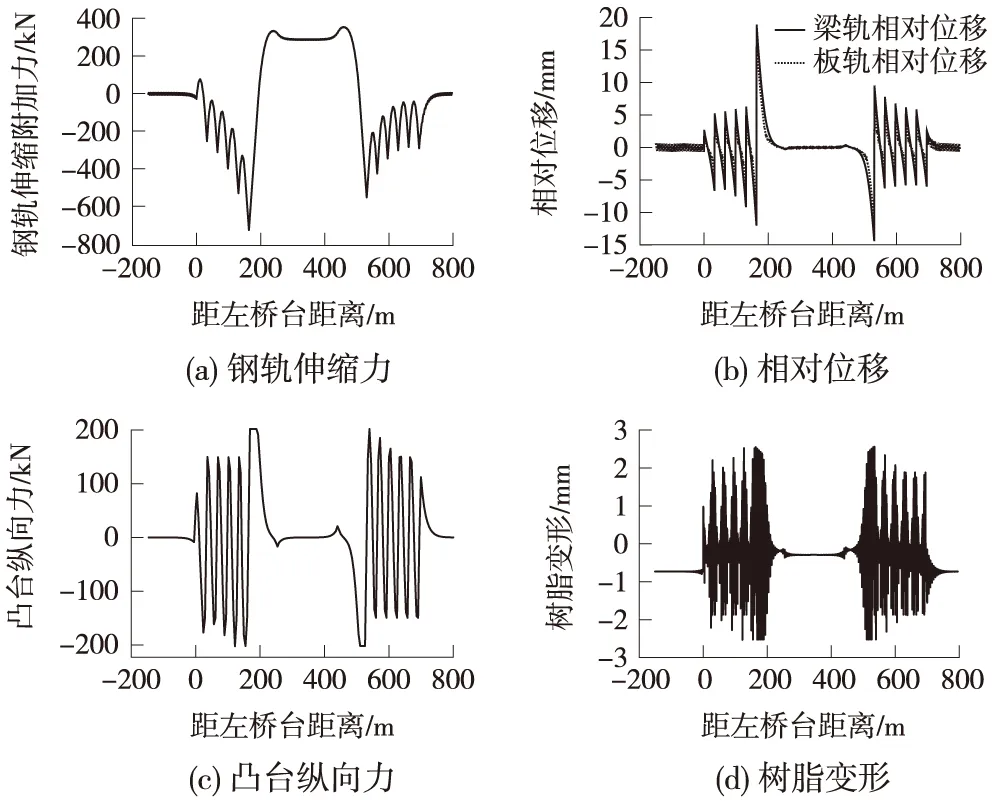
图2 梁体及轨道板升温条件下计算结果

从图2可以看出，钢轨伸缩附加力最大值出现在刚构梁的左侧梁端处，是因为左侧梁端处的梁轨相对位移最大。且温度升高较大时，由于轨道板与CA砂浆之间的摩阻力不能够完全阻止梁轨相对位移，从而使轨道板压缩凸型挡台周围树脂，凸台树脂变形进而提供部分纵向阻力。凸型挡台周围树脂变形量未超过3 mm，满足规范要求。

3 桥墩纵向温度梯度下轨道各部件的受力、变形分析

目前在我国《铁路无缝线路设计规范》未考虑该温度梯度荷载，暂按德铁桥梁设计规范DS804取温差为5 ℃。并且假设桥墩温差沿墩高方向均匀分布，不计桥墩基础和上部结构对墩顶纵向位移的影响，桥墩任一截面内温度变化为线性。

在文献[4]中，桥墩采用弹簧单元模拟，把温度梯度引起的墩顶位移直接施加到弹簧上，这样存在一定的缺陷，因为实际是轨-梁-墩共同作用的结果，若把上部无任何约束下产生墩顶位移作为定值施加在系统中不合理。因此对于桥墩运用能直接施加温度荷载的梁单元。由于两侧的简支梁桥桥墩高度较低，其自身在温度荷载作用下的变形很小，因此不考虑其温度变化。以1号、2号桥墩两侧温差5 ℃为例，计算结果如图3所示，墩顶位移和墩台力如表2所示。

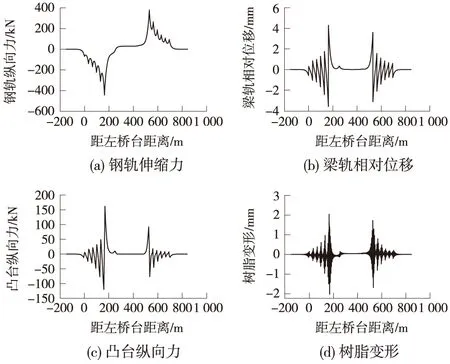
图3 桥墩整体升温时计算结果

钢轨附加力/kN墩台1号纵向力/kN墩台2号纵向力/kN梁轨相对位移/mm凸台纵向力/kN树脂压缩量/mm树脂离缝/mm440.694-2952.110-336.6274.343160.7182.0082.025

从图3及表2中可以得到，刚构桥虽然左右对称，但由于刚构桥墩高度差的存在，使得梁端处钢轨纵向力的大小和墩台纵向力存在差异。同样凸台树脂的变形未超过规范规定限值。对于高墩大跨连续刚构桥梁，结构属于超静定结构，在温度荷载作用下产生的桥墩墩顶偏转与桥墩刚度取值有密切关系，因此，有必要研究桥墩刚度变化时桥墩纵向温度梯度对桥上无缝线路受力和变形的影响。计算中通过修改模拟桥墩的梁单元的弹性模量来实现桥墩刚度的改变，主要考虑了桥墩刚度为原始刚度的0.1、0.5、1、2倍4种工况，计算结果见图4。

图4 不同桥墩刚度时计算结果

图5为不同刚度下的钢轨附加力、梁轨相对位移、凸台纵向力和树脂变形的最大值变化情况。

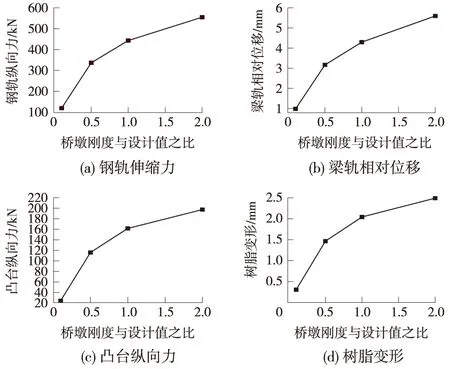
图5 不同桥墩刚度与设计值之比时计算结果

从图4、图5可以看出，随着桥墩刚度的增大，在相同温度梯度作用下，钢轨附加力，梁轨相对位移，凸台纵向力和树脂变形均相应增大。这是由于墩台刚度越大，则在温度梯度荷载作用下桥墩墩顶偏转量越大，从而带动上部梁体和钢轨之间产生更大的相对位移。且从图中可以看出，当桥墩刚度为设计值的0.1倍时，对应的钢轨附加力仅为107.900 kN，占第2节计算钢轨附加力的14.85%，当桥墩刚度为设计值的2倍时，对应的钢轨附加力为555.204 kN，占第2节计算钢轨附加力的76.40%，可见刚度的大小对桥墩纵向温度梯度荷载、对桥上无缝线路具有重要的影响。

同时考虑桥墩温度梯度和梁体、轨道板温升时，对轨道各部件的受力和变形的影响，计算结果如图6所示，墩台力和墩顶位移见表3。

图6 梁体、轨道板+桥墩温度梯度计算结果

墩编号工况12仅梁体轨道板升温墩底纵向力/kN2921.524-3615.573梁体、轨道板+桥墩升温墩底纵向力/kN309.984-3515.145

从图6(a)中可以看出，由于温度梯度荷载的作用，使得钢轨附加力增加较大，此时的钢轨附加力为1038.790 kN，相比仅梁体温升时的钢轨附加力增加了311.520 kN，但相比于仅受温度梯度荷载作用下的钢轨附加力440.694 kN要小，这是由于扣件阻力的非线性引起的。从图6(c)、(d)中可以看出，即使在钢轨附加力增加较大的情况下，凸台纵向力和树脂变形均几乎无增长，这是因为当凸形挡台周围树脂层强度满足设计值时，凸台所受最大纵向力不会超过轨道板上所有扣件纵向阻力之和。从表3可以看出，考虑桥墩温度梯度作用后，两刚构墩的墩台力会降低，这是由于温度梯度荷载下产生的墩台力和梁体升温作用下产生的墩台力方向相反，进而产生叠加抵消作用，这与温度梯度荷载施加的方向有关，检算时应该考虑最不利的组合来检算墩台刚度。

4 结论及建议

(1)对于高墩大跨桥上无缝线路的设计，不能仅仅考虑伸缩、挠曲、制动和断轨等

工况的作用，还需考虑对高墩大跨桥梁有较大影响的一些特殊荷载的作用。

(2)在桥墩温度梯度荷载下，会产生较大的钢轨附加力，且随着桥墩刚度的增加进一步增加。但考虑温度梯度和梁体温升组合作用时，明显小于各单独作用之和。建议根据实际情况确定温度梯度荷载大小和形式之后，对高墩大跨桥上无缝线路设计或检算时考虑桥墩温差的影响，并与梁体温升耦合计算。

(3)无论从仅考虑梁体温升，还是同时考虑梁体温升和桥墩温度梯度，凸台纵向力和树脂变形均几乎无增长，凸台所受最大纵向力不会超过轨道板上所有扣件纵向阻力之和，因此凸台树脂压缩量也不会超过规范规定限值3 mm。

[1]刘浩.风荷载对高墩大跨桥梁桥上无缝线路的影响[J].铁道建筑，2013(12):15-18.

[2]张梦楠.高墩大跨桥梁桥墩升温对桥上无缝线路的影响研究[J].铁道标准设计，2014(9):32-35.

[3]胡志鹏.高墩大跨桥梁桥墩沉降对桥上无缝线路的影响[J].铁道标准设计，2013(10):23-26.

[4]李阳春.桥墩温差荷载作用下桥上无缝线路钢轨附加力研究[J].铁道建筑，2008(2):6-9.

[5]王彪.连续梁桥上CRTSⅠ型板式无砟轨道凸形挡台纵向力分析[J].铁道建筑，2013(3):117-120.

[6]中华人民共和国铁道部.TB10015—2012铁路无缝线路设计规范[S].北京:中国铁道出版社，2013.

[7]谢铠泽.桥上单元板式无砟轨道无缝线路的适应性[J].西南交通大学学报，2014，49(4):649-655.

[8]曲村.高速铁路长大桥梁CRTSⅠ型板式无砟轨道无缝线路力学特性分析[J].铁道标准设计，2011(4):13-17.

[9]全顺喜.高速道岔几何不平顺动力分析及其控制方法研究[D].成都:西南交通大学，2012.

[10]李秋义.桥墩温差荷载引起的桥上无缝线路钢轨附加力[J].中国铁道科学，2007(4):50-54.

[11]朱浩.连续刚构桥桥墩刚度对桥上无缝线路的影响[J].铁道建筑，2014(1):109-111.

[12]张扬.高墩大跨刚构-连续组合梁桥的设计[J].铁道标准设计，2011(4):80-82.

[13]张宁.高墩大跨连续刚构桥桥墩稳定性分析[J].北方交通，2013(1):39-41.

[14]杨艳丽.铺设无缝线路的桥梁墩台纵向线刚度设计研究[D].长沙:中南大学，2008.

[15]张亚爽.高墩水平温差对连续刚构桥上无缝线路影响[J].铁道标准设计，2014(11):20-24.

Effects of Pier Temperature Gradient on Ballastless Track of Long-span Bridge

LUO Hua-peng, XING Jun, YANG Kai, WANG Ping

(MOE Key Laboratory of High speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Due to solar radiation, both sides of a bridge are subjected to different temperatures. Where the height of a pier is larger, the pier will experience a greater longitudinal displacement, forcing the beam body, the track slab and the rail to displace, generating additional stress on CWR on the bridge. In order to understand the law of force and deformation of the ballastless track under pier temperature gradient, a line-bridge-pier integration model of CWR is established based on the beam-track interaction principle and the finite element method. The results show that the additional stress on the rail increases with the increase of the piers stiffness in perspective of only the vertical temperature gradient of pier load. In consideration of both the beam heating and the vertical temperature gradient, the additional rail stress is less than that when the stress generated by beam heating or vertical temperature gradient is considered respectively. The boss stress and resin deformation are not changed greatly regardless of the only pier vertical temperature gradient, or both the beam heating and vertical temperature gradient.

High pier and long span continuous rigid frame; Temperature gradient; CWR; Resin deformation

中央高校基本科研业务费资助项目(SWJTU12CX079)

罗华朋(1991—)，男，硕士研究生，E-mail：756468322@qq.com。

1004-2954(2015)08-0026-04

U213.2+44

A

10.13238/j.issn.1004-2954.2015.08.006