粗糙集属性约简算法综述
唐卫国张 涛罗 奕徐晋勇
(1.广西壮族自治区右江矿务局有限公司,广西 百色 531501;2.桂林电子科技大学,广西 桂林 541004)
粗糙集属性约简算法综述
唐卫国1张 涛2罗 奕2徐晋勇2
(1.广西壮族自治区右江矿务局有限公司,广西 百色 531501;2.桂林电子科技大学,广西 桂林 541004)
属性约简是粗糙集理论中最核心的问题。文章阐述了基于信息熵、可辨识矩阵、遗传算法、Johnson等粗糙集属性约简算法流程,指出了粗糙集属性约简算法的现有问题及发展趋势,促进粗糙集属性约简的研究进一步发展。
属性约简;粗糙集理论;算法
随着计算机网络的高速发展,人们所要处理的数据越来越多。在大量数据中会伴有不确定问题。目前处理不确定性问题的方法主要包括概率统计、模糊理论、证据理论等[1]。但这些方法必须依靠大量的先验知识。粗糙集理论很好弥补了以上方法缺点,可以有效处理不确定信息,却不需要任何先验知识[2]。
粗糙集约简是粗糙集理论中最重要一环,包括值约简和属性约简两种。目前,大量的研究都是侧重于属性约简[3]。属性约简,就是在保证系统本身含义前提下,删除其中多余或重复的属性,保留起决定作用的核心属性。通过属性约简,可以在不改变系统本身含义的前提下得到更简洁的决策属性。
对于信息表I(U,A),如果有属性集B⊆A,且满足ind(B)=ind(A),则称B为A的一个约简,记为red(A)。ind(A),ind(B)代表着A和B上的不可分辨关系。

集A所有约简的交集称为A的核,记为core(A),即:
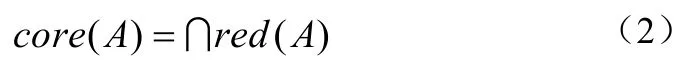
core(A)含有属性集A的全部约简集合中共同的等价关系,是属性集A中最重要集合。核的定义表示了核属性是约简属性集中一部分,利用核属性可以更迅速的进行属性约简,改变属性核属性就会影响属性约简的前后一致性[4]。
1 粗糙集约简算法初探
1.1基于信息熵的约简算法

属性集M相对于属性集K的条件熵H(K|M)为:
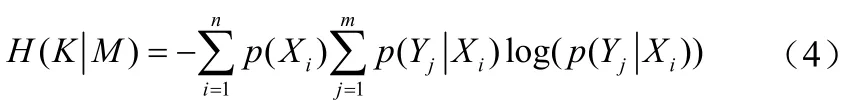
属性集M同属性集K的互信息为:
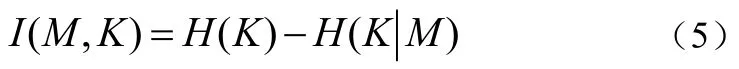
基于信息熵的约简算法流程为:
步骤1:针对决策表S=(U,C∪D,V,f ),计算决策属性D的信息熵H(D);
步骤2:计算条件属性C同决策属性D的互信息量I(C,D);
步骤3:求核属性。初始化core=ø,对∀a∈C,有f(x, D)≠f(y,D),且f(x,C-a)= f(y,C-a),属性a就为决策表的核属性;
步骤4:令R等于核属性,并计算R同决策属性D的互信息量I(R, D);
步骤5:对∀a∈C-R,计算其同决策属性D的互信息量I(a, D),找出使互信息量最大的属性a,且R=R∪{a};
步骤6:计算此时属性R同决策属性D的互信息量I(R,D),判断属性R的信息量和条件属性C的信息量是否相等,如果是就停止运算;否则转至步骤5。
1.2基于可辨识矩阵的约简算法
基于可辨识矩阵约简算法的流程为:
步骤1:针对知识表达系统S=(U, C∪D,V,f ),C为条件属性,D为决策属性,a(x)、D(x)为第x条记录对应属性的值。建立决策表的可辨识矩阵M=(mij)n×n。(mij)n×n有如下定义[6]:
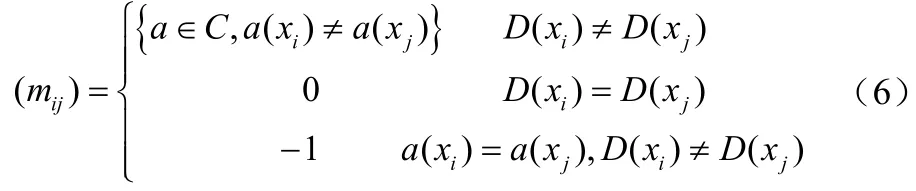
其中i,j=1,2,…,n。
步骤2:如果M=(mij)n×n中存在单属性元素,则将其归入集合R,集合R就称为核属性,并转至步骤4,否则建立可辨识矩阵中非零元素的析取表达式:

其中ai为非零元素mij中的属性项。
步骤3:对任意Ri=R(i=1, 2, …, n),如果Ri∈M,则令M中与Ri对应元素等于0,得到新的矩阵M′。对新矩阵M′中的所有非零元素建立析取表达式:

ai为非零元素mij中的属性项。
步骤4:将析取表达式进行合取运算,得到合取范式为:

步骤5:将合取范式L转换为析取范式:

步骤6:将核属性R中的属性插入L′中的每个析取范式中,得到的每一组集合就为一个属性约简结果。基于可辨识矩阵约简算法得到的约简结果通常都不止一组。
1.3基于遗传算法的约简算法
定义2 在一个知识表达系统中,P、Q分别为论域中的属性集合。当
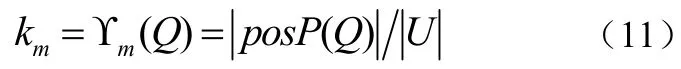
称属性Q是km度依赖于属性P的,︱·︱表示属性集合中包含对象个数。
定义3 令属性子集PP′⊆,则P′关于Q的重要性定义为:
特别的,当P′={a}时,属性a∈P关于Q的重要性定义为:
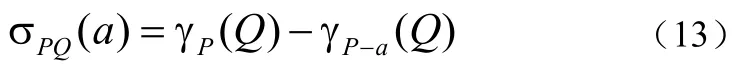
定义4 适值函数是在遗传算法中评价个体位串适应性的标准,定义为[7]:
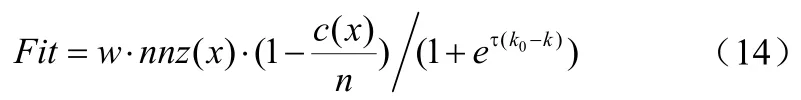
每个个体被选择的概率可以表示为:
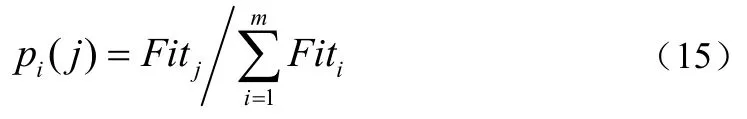
其中n表示条件属性的数量,c(x)表示个体所含条件属性的数量,k表示全部条件属性相对于决策属性的依赖度,kp为每个个体包含的条件属性相对于决策属性的依赖度。
根据以上定义,遗传算法的流程为:
步骤1:知识表达系统S=(U,C∪D,V,f ),由公式(12)计算条件属性C相对于决策属性D的依赖度kp;
步骤3:产生n个长度为r的初始种群,个体中每一位对应一个条件属性;
步骤4:计算每个个体所含条件属性相对于决策属性D的依赖度kp,并利用式(14)计算出适值最大的个体传递给下一代;
步骤5:对于规模为n的种群,计算其每个个体适值及被选择的概率,得出被选择的期望数。以轮盘赌的方式对个体进行挑选,组成新的种群;
步骤6:对种群进行交叉和变异操作,并针对于现阶段的每个个体,再次计算所含条件属性相对于决策属性的依赖度kp和每个个体的适值;
步骤7:判断遗传算法是否成熟(连续n代的最优个体适值不继续增加),如果最优个体的依赖度k=kp,且该属性集合的具有独立性,则停止运算,否则转至步骤5。
1.4基于Johnson算法的约简算法
Johnson算法是一个新型约简算法,由用户来决定属性的权重,从而可以快速地计算出约简组合[8]。选取当前频率最大的属性加入约简组合,如果一个属性出现次数的频率越大,它的可分辨能力就越强。而且Johnson算法得出的约简组合只有一组,相比于其他方法更加直观。设定R表示约简,其算法流程为:
步骤2:计算可分辨矩阵M,M={mij:mij≠ø};
步骤3:计算属性ai在M中出现的次数ωai(M);
步骤4:选择使ωai(M)最大的属性记为a,R=R∪{a};
步骤5:将M中包含a属性的全部删除;
步骤6:如果M=ø,停止计算,否则转至步骤3。
2 属性约简方法存在问题发展趋势
粗糙集理论的优越性在很多实际应用中得到了证明,其属性约简仍有一些间题有待解决。下面列举一些今后可能的研究方向。
(1)如何提高约简算法的效率,降低算法的执行效率和复杂度,是进一步研究粗糙集理论的关键部分;
(2)当属性值不是一个固定值,而是一个连续区间时,如何将数据进行合理的离散化处理,直接从这类信息系统中获取知识是一个值得研究的问题;
(3)属性约简方法众多,在实际应用中可以互相融合,提高约简速度。如很多方法就使用可辨识矩阵来获取核属性集[9]。
3 总结
本文总结了现有粗糙集属性约简方法,分析了现有方法的存在缺点,并提出了未来的发展趋势。粗糙集属性约简方法的不断完善对如何在大数据时代做出正确的决策具有重要的理论和现实意义。
[1] 王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1246.
[2] 汤建国,祝峰,佘堃.粗糙集与其他软计算理论结合情况研究综述[J].计算机应用研究,2010,27(7):2404-2410.
[3] 黄楠.基于粗糙集和模糊聚类方法的属性约简算法[J].电脑知识与技术,2012,8(32):7718-7719.
[4] 谭旭.改进分辨矩阵下的增量式条件属性约简算法[J].系统工程理论与实践,2010,30(9):1684-1694.
[5] 陈媛,杨栋.基于信息熵的属性约简算法及应用[J].重庆理工大学学报(自然科学),2013,27(1):42-46.
[6] Yiyu Yao, Yan Zhao. Discernibility Matrix Simplification for Constructing Attribute Reducts[J]. Information Sciences, 2009, 179(17):867-882.
[7] 颜艳,杨慧中.基于遗传算法的粗糙集属性约简算法[J].计算机工程与应用,2007,43(31):156-158.
[8] 陈桂芬,马丽,董玮.聚类、粗糙集与决策树的组合算法在地力评价中的应用[J].中国农业科学,2011,44(23): 4833-4840.
[9] Junbo Zhang, Tianrui Li, Da Ruan, et al. Rough Sets based Matrix Approaches with Dynamic Attribute Variation in Set-valued Information Systems[J]. International Journal of Approximate Reasoning,2012, 53(4):620-635.
A survey of rough set reduction process algorithm
Attribute reduction is most important issue in the rough set theory. This paper describes rough set reduction process algorithm based on information entropy, discernable matrix, genetic algorithms, Johnson algorithms, pointing current problems and developing tendency in rough set reduction process algorithm, motivating higher research development of rough set reduction process algorithm.
Rough set;reduction process;algorithm
O13
A
1008-1151(2015)11-0017-03
2015-10-12
广西科学研究与技术开发计划(桂科能1598020-8)。
唐卫国(1974-),广西壮族自治区右江矿务局有限公司工程师,研究生学历,硕士,研究方向为矿山通风与安全工程。
徐晋勇(1962-),男,桂林电子科技大学教授,博士,从事金属材料表面改性、机械工程及其产业化的研究。

