一种自适应目标机动的αβγ滤波算法

张 瑞 谢 敏 雷 瑛

（西安电子工程研究所，陕西 西安 710100）

一种自适应目标机动的αβγ滤波算法

张 瑞 谢 敏 雷 瑛

（西安电子工程研究所，陕西 西安 710100）

针对传统的α-β-γ滤波算法在跟踪机动目标时性能下降的问题，文章提出一种自适应目标机动的α-β-γ滤波算法。该算法是基于多模型混合估计的思想，用残差构建模型失配度，进而迭代更新模型概率，使跟踪滤波器自适应地调节，达到更好的跟踪效果。仿真结果表明，与传统α-β-γ滤波算法相比，对于机动性较强的目标，该算法具有更好的跟踪性能。

α-β-γ滤波；机动目标跟踪；多模型混合估计

随着自动化技术和人工智能技术的不断发展，越来越多的无人飞行器，智能导弹和智能炮弹将出现在战场中。以美军的X-47B无人战斗机为代表的先进无人机，摆脱了驾驶员生理承受力和反应力的限制，可以做到高速、高机动性。同时，计算机硬件设备性能的不断提升支持着控制算法和软件的不断发展，可以预见未来的无人飞行器，智能导弹和智能炮弹将是具有复杂运动状态的高机动目标。

所谓目标机动，是指目标的加速度的方向和幅度在短时间内出现急剧地变化，表现为急转弯、急加速和急减速。针对目标的机动，传统的α-β、α-β-γ和卡尔曼滤波算法均出现了性能下降，因此需要对适应高机动目标的跟踪滤波算法进行研究。α-β和α-β-γ滤波算法由于增益计算量小，且可以离线计算，在工程中得到广泛应用。但是由于增益固定，传统的α-β和α-β-γ滤波算法对于机动目标的跟踪性能下降明显。本文提出一种基于多模型混合估计的自适应α-β-γ滤波算法，有效提高了对于机动目标的跟踪性能。

1 α-β-γ滤波算法

α-β-γ滤波器实质上是运动方程为匀加速的卡尔曼滤波器的稳态解形式[1]。假设目标做匀加速直线运动，此时状态向量为

其中，x1，x2,x3分别代表目标的位置、速度、加速度。

则系统的状态方程为

噪声w(k-1)为均值为0，协方差阵为Q的正态噪声。量测方程为

则相应的卡尔曼滤波公式为

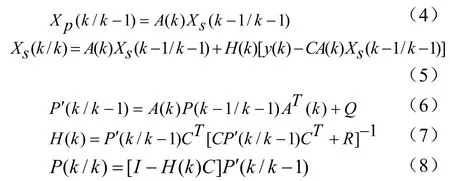
当卡尔曼滤波递推足够多步后，增益向量()H k将趋于常数向量H，即得到滤波公式

根据α-β-γ滤波与卡尔曼滤波的关系，如果卡尔曼滤波稳定后，预测协方差阵为

则α-β-γ滤波器的增益满足

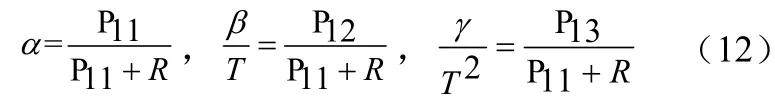
其中，R为量测噪声的方差

由此可见，α-β-γ滤波对应着相应卡尔曼滤波的稳态解，增益系数不随迭代改变，计算量小。但是传统的α-βγ滤波器增益无法随着目标的运动模型的改变而改变，固定的增益无法适应机动目标的跟踪。

2 自适应多模型α-β-γ滤波算法

目前得到广泛应用的目标跟踪算法是卡尔曼滤波算法、α-β和α-β-γ滤波算法，但均在跟踪机动目标时存在不足。对于卡尔曼滤波，当系统达到稳态时，其预测协方差将趋于极小值，使得滤波器的增益也趋于极小值，此时若状态发生突变，残差增大，预测协方差和滤波器的增益不能随残差同步改变[2]。而对于α-β和α-β-γ滤波算法，增益为常量，不随残差改变。因此，不具有对机动目标良好的跟踪能力。针对这个问题，C.B.Chang和R.H.Whiting等人将可调白噪声模型的思想应用于机动目标跟踪。这种方法通过观测目标滤波残差的变化来判断机动的产生与结束，并对滤波器进行相应的调整。但这种方法需要先人为设定门限，不同的门限对应不同的跟踪性能。同时，该算法只适用于卡尔曼滤波，无法优化α-β和α-β-γ滤波算法。

在使用基于单模型的滤波算法进行机动目标跟踪时，滤波模型需要先验设定，但是先验滤波模型不能较好地匹配目标的机动，因此其跟踪效果往往不好，特别是当前目标机动能力日益增强，目标运动模式的结构、参数变化起伏很大，导致单模型算法很难及时准确地辨识机动参数，从而造成模型的不准确，而导致算法的性能下降[3]。为了适应目标机动，根据目标机动时残差增大的特点，本文提出一种自适应多模型α-β-γ滤波算法:

2.1先验滤波模型的确定

已知k时刻的残差为

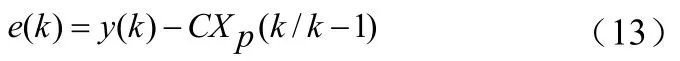
当目标非机动且滤波收敛时，根据α-β-γ滤波与卡尔曼滤波的关系，可知残差的方差为

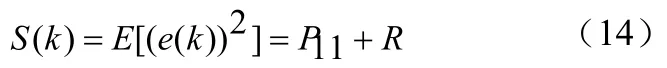
即， ()e k服从均值为0，方差为 11+PR的正态分布[3]。当目标机动时，残差 ()e k为非平稳随机过程，并且幅度急剧增大。

α-β-γ跟踪滤波器的收敛速度和精度取决于增益系数α、β、γ的选取。在选取增益系数时，必须折中考虑噪声特性与动态性能之间的平衡[1]。研究表明，最优增益系数应满足如下关系[4]：

其中，ξ为平滑系数，也是系统特征方程的三重正实根。所以，在最优的情况下,可以利用平滑系数ξ来确定α、β、γ的值。不同的平滑系数ξ，决定了不同的滤波模型。由式（12）和式（15）可得

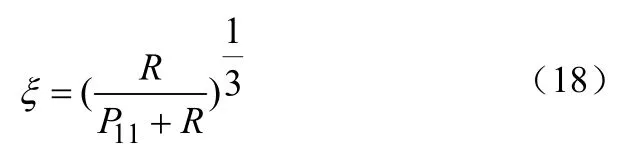
这说明，可以根据先验参数R和 11P确定先验平滑系数 1ξ。其中，R为量测噪声方差， 11P为预测协方差阵的第一项，即目标位置的预测误差的方差。由先验设定确定的先验平滑系数 1ξ代表着先验α-β-γ滤波器模型。

2.2自适应多模型α-β-γ滤波算法原理

自适应多模型α-β-γ滤波算法的原理图如图1：

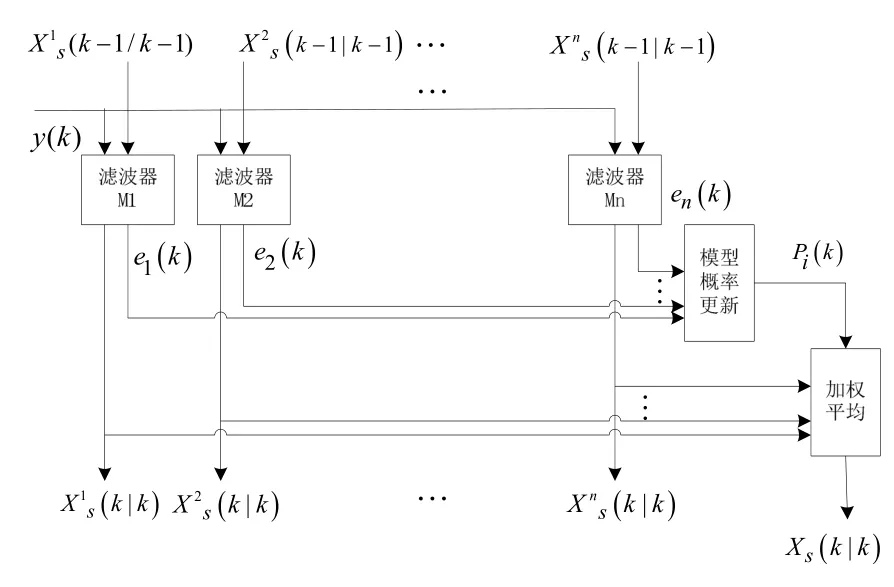
图1　自适应多模型α-β-γ滤波算法的原理图

多模型算法的关键是模型概率的计算。本文提出一种滤波模型失配度，用表示，计算公式为

式（19）也可以写为

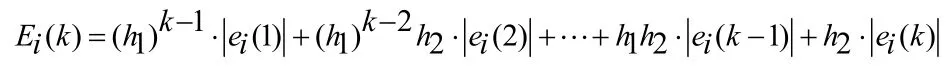
式（19）采用序贯式结构对各个时刻的残差幅度加权地进行积累，得到滤波模型失配度。从中可以看出是迭代计算的，因此不需要存储大量数据。为了增加新数据的权重， 1h通常取小于1的正数，作为衰减因子。

式（20）表示，滤波模型失配度越大，则滤波器的模型概率越小。在得到 k时刻的滤波器集合的模型概率后，就可以混合估计k时刻的滤波值

通过式（21）可以看出，算法自适应地控制了各个滤波器的权重，使得对目标跟踪性能较好的滤波器权重加大，对目标跟踪性能较差的滤波器权重减小。

2.3仿真分析

如果由先验信息知道量测噪声方差 R为 100m2，目标的跟踪误差的方差为 25m2，则由此计算得0.9283 =。进而计算得系数。如果采样间隔设定为 T=0.5s，则初始滤波模型的增益向量为。

对目标的跟踪一般都是多维上同时跟踪滤波，只有每一维上跟踪效果都好，整体的跟踪效果才能好。本文仿真对一个运动目标在 X轴这一维上的跟踪滤波。目标的起始点在10000m处，起始量测值为10020m，目标在X轴这一维上的运动状态如表1所示：

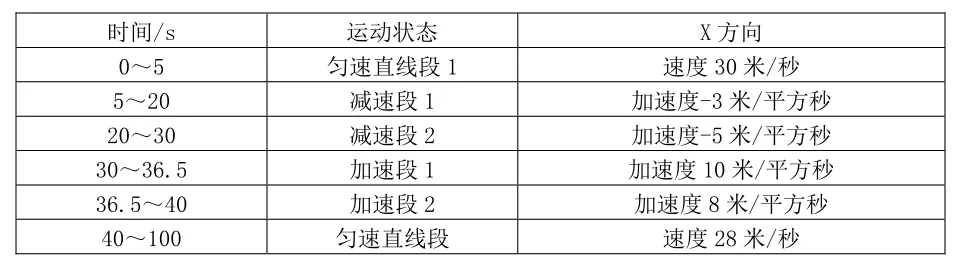
表1　运动状态

使用初始α-β-γ滤波器对目标的跟踪滤波效果如图 2所示，预测误差幅度如图3所示：

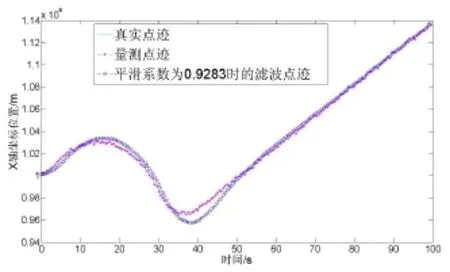
图2　初始α-β-γ滤波器滤波效果

图3　初始α-β-γ滤波器滤波误差幅度

从图2和图3可以看出，在目标出现较强机动的时候，初始α-β-γ滤波器的预测误差急剧增大。在目标机动最强的加速段1和加速段2上目标预测误差达到最大，进入目标匀速直线运动段后，预测误差逐渐减小，但减小速度较慢，到[70s,100s]段时预测误差已经减小到低于量测噪声了，才达到较好的跟踪效果。

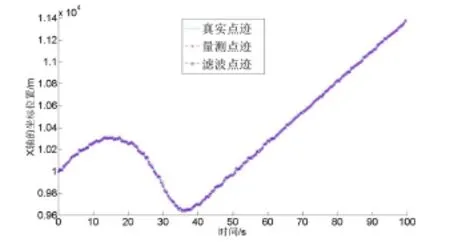
图4　自适应多模型α-β-γ滤波的滤波效果

图5　自适应多模型α-β-γ滤波的滤波误差幅度

从图4和图5可以看出，自适应多模型α-β-γ滤波算法有效地改善了对较强机动目标的跟踪性能。在目标非机动和机动时，算法的滤波误差幅度总体上小于量测噪声幅度，得到了较好的跟踪效果。

3 结论

针对单模型α-β、α-β-γ和标准卡尔曼滤波算法对于机动目标跟踪性能下降的问题，本文基于多模型混合估计思想，提出了一种自适应多模型α-β-γ滤波算法。仿真结果表明，该算法可以较好地适应目标的机动，对目标的跟踪性能较好。但该算法需要多模型并行运算，计算量较大。同时，模型集合如何选取最优以及模型概率如何计算最优，这些问题仍需要进一步研究解决。

[1] 黄鹤,张会生,许家栋,等.一种改进的α-β-γ滤波跟踪算法[J].西北工业大学学报,2008,26(2):146-151.

[2] 高增敏,王首勇,郑作虎,等.一种适用于机动目标跟踪的改进卡尔曼滤波算法[J].空军雷达学院学报,2011,5(25): 339-342.

[3] 何友,修建娟,张晶炜,等.雷达数据处理及应用(第二版) [M].北京:电子工业出版社,2009:160-161.

[4] Tenne D. Optimal Design of α-β-γ Filters. Proceedings of the American Control Conference[J].Chicago IL USA, 2000,(6):4348-4352.

[5] Y.Bar-Shalom,T.E.Fortmann.Tracking and Data Association[M]. Academic Press,1988.

[6] 李从文.基于输入估计的滑窗式目标机动检测算法研究[D].南京:南京理工大学,2010.

Multiple model algorithm based on α-β-γ filter for tracking maneuvering targets

In consideration of the performance degradation of traditional α-β-γ filter in tracking maneuvering targets, a multiple model algorithm based on α-β-γ Filter is presented. It is based on the method of multiple model estimation, using the residual to update probabilities of models and adjust the filter adaptively. The simulation results show that compared with the traditionalα-β-γfilter, this algorithm has better tracking performance for maneuvering targets.

α-β-γ filter; tracking maneuvering targets; multiple model estimation

TP11

A

1008-1151(2015)11-0012-03

2015-10-11

张瑞（1990－），男，陕西榆林人，西安电子工程研究所硕士研究生，研究方向为雷达总体技术；谢敏（1991－），女，陕西西安人，西安电子工程研究所硕士研究生，研究方向为固态发射机技术；雷瑛（1982－），女，陕西西安人，西安电子工程研究所工程师，研究方向为雷达信息处理、实时控制技术。