一类非拟单调型非局部时滞扩散方程的行波解

严 升 赵海琴

（咸阳师范学院数学与信息科学学院，陕西 咸阳 712000）

一类非拟单调型非局部时滞扩散方程的行波解

严 升 赵海琴

（咸阳师范学院数学与信息科学学院，陕西 咸阳 712000）

研究一类非拟单调型非局部时滞扩散方程的行波解。通过构建两个辅助的拟单调方程，并利用肖德尔不动点定理证明了行波解的存在性。结果表明，此类非拟单调型非局部时滞反应扩散方程的行波解对所有时滞0τ≥是持久存在的。

行波解；存在；非局部扩散；肖德尔不动点定理

1 引言

近几年，非局部扩散方程备受关注，且已经有了很多的结果[1-3,7]。此类方程源于许多实际的领域，例如转化模型[1]，材料科学模型[2]等。众所周知，时间滞后(简称时滞)在许多过程中都是不可避免的。行波解是偏微分方程的一类特殊的解，具有理论和应用双重意义。因而非局部时滞扩散方程的行波解问题引起了数学家们的广泛关注，见例[8,9]。事实上，如果当非局部时滞扩散方程是拟单调的，我们就可以应用上下解的方法在建立行波解的存在性，见[8]。如果当非局部时滞扩散方程是非拟单调的，那么行波解的求解问题将会变的更为复杂。对于这类不具有拟单调性的非局部时滞扩散方程，只有文献[9]研究了行波解的存在性。然而，这些结果只对时滞充分小时是有效的。因此，有必要进一步研究非拟单调型非局部时滞扩散方程的行波解问题。

本文研究如下形式的非拟单调型非局部时滞扩散方程行波解的存在性：

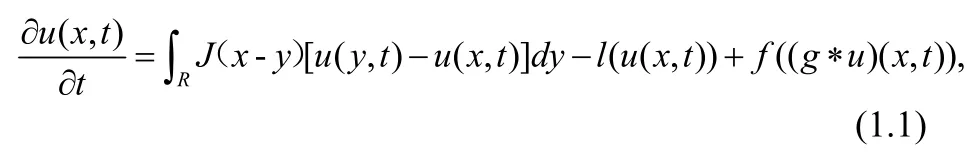
如果U(⋅):R→是单调的，则称U是一个行波前解。

在假设（A0）-（A4）的条件下，我们建立了非拟单调方程（1.1）的行波解的存在性。主要方法是基于构造两个拟单调的辅助扩散方程并利用肖德尔不动点定理.这种方法最初是文献[6]对一类时滞反应扩散方程发展的。

2 预备知识

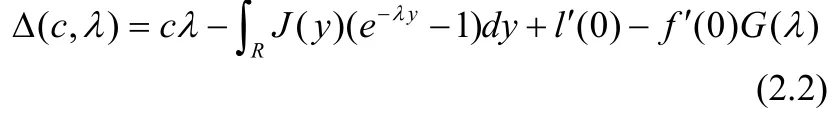
运用[8]相似的方法我们可以很容易建立拟单调情形下方程（1.1）行波解的存在性，证明从略.

3 非单调情况下的行波解

本节，应用上面的结论来证明我们的主要定理。为此，首先需要构建两个拟单调的非局部辅助时滞扩散方程，类似于文献[6]，我们定义了如下的两个连续函数：

引理3.1 假设条件（A0）-（A4）成立，那么下面的语句成立：

(i)方程*(u)f和(u)fε在是连续的并且在上是递增的.

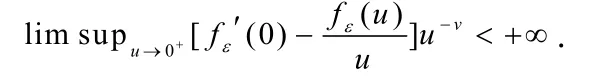
考虑如下两个拟单调非局部辅助迟滞扩散方程：

下面的引理可由引理2.2和3.1直接得出.

证明：设

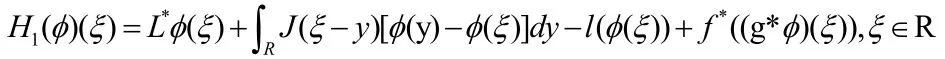
定义

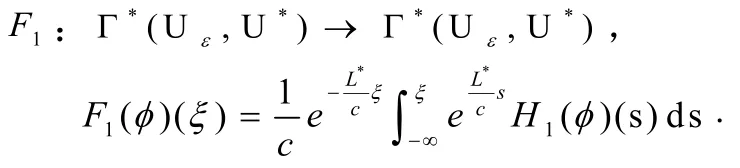
引理3.5 假设条件（A0）-（A4）成立，则

证明：证明是显然的，从略.

定理1.1的证明：通过引理3.5和肖德尔的不定点定理，可知方程在上有一个不动点U满足：

则我们有

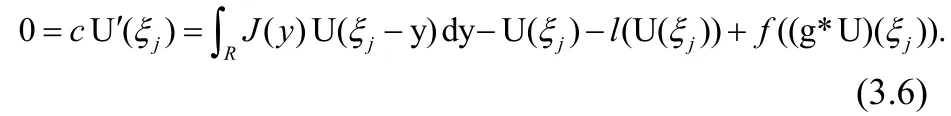
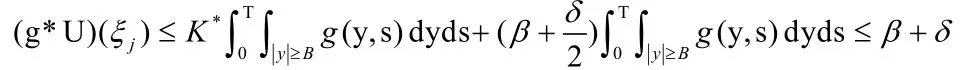
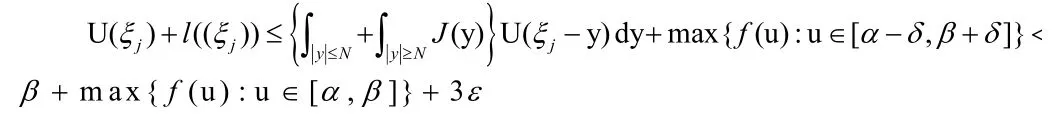
运用类似的方法，可以得到

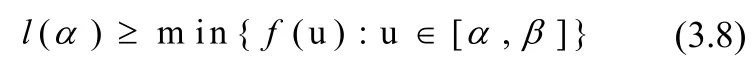
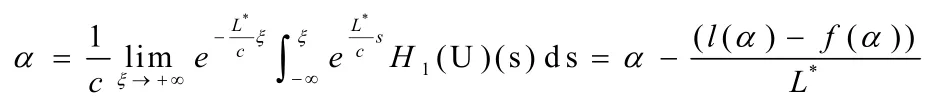
证毕

[1] P.W. Bates, P.C. Fife, X. Ren, X. Wang, Traveling waves in a convolution model for phase transition, Arch. Rational Mech. Anal.,1997 ,(138):105-136.

[2] P.W. Bates, On some nonlocal evolution equations arising in materials science, In Nonlinear dynamics and evolution equations (Ed. by H. Brunner, X. Zhao, X. Zou),13-52, Fields Inst. Commun.,48,Amer. Math. Soc.,Providence, RI,2006.

[3] Z. Chen, B. Ermentrout, X. Wang, Wave propagation mediated by GABAB synapse and rebound excitation in an inhibitorynetwork:Areducedmodelapproach, J.Computational Neuroscience,1998,(5):53-69.

[4] X. Chen and J.-S. Guo, Existence and asymptotic stability of traveling waves of discrete quasilinear monostable equations, J. Dierential Equations, 2002,(184):549-569.

[5] S.W. Ma, X. Zou, Existence, uniqueness and stability of travelling waves in a discrete reaction-diffusion monostable equation with delay, J. Differential Equations, 2005,(217): 54,87.

[6] S.W. Ma, Traveling waves for nonlocal delayed diffusion equations via auxiliary equations, J. Differential Equations, 2007, (237):259-277.

[7] S.X. Pan, W.T. Li, G. Lin, Travelling wave fronts in nonlocaldelayedreaction-diffusionsystemsand applications, Z. angew Math. Phys.,2009, (60):377-392.

[8] S.X. Pan, Traveling wave fronts of delayed non-local diffusion systems without quasimonotonicity, J. Math. Anal. Appl.,2008,(346):415-424.

Traveling wave fronts in a non-quasi-monotone reaction-diffusion equation with nonlocal delay

This paper is concerned with the traveling waves for a class of non-quasi-monotone reaction-diffusion equations with nonlocal delay.The existence of traveling waves is proved by constructing a profile set in a suitable Banach space and applying Schauder's fixed point theorem. The result implies that the traveling waves of the reaction-diffusion equations with nonlocal delay are persistent for all values of the delay0τ≥.

Traveling waves; existence; non-local diffusion; Schauder's fixed point theorem

O175.14

A

1008-1151(2015)04-0030-03

2015-03-12

咸阳师范学院省级大学生创新创业训练计划资助项目(编号 1816)；咸阳师范学院校级大学生创新创业训练计划资助项目(编号2013029)。

严升，咸阳师范学院数学与信息科学学院教师。