伸缩梯度投影法在天文图像复原中的应用

邵云龙

（桂林电子科技大学，广西 桂林 541004）

伸缩梯度投影法在天文图像复原中的应用

邵云龙

（桂林电子科技大学，广西 桂林 541004）

在地基天文观测中，由于大气湍流的干扰，使得观测结果降质，严重影响高分辨率天文图像的获取，因此需要对天文图像进行复原。基于伸缩梯度投影（SGP）的图像反卷积算法精度高、收敛快，但需要较为精确的点扩散函数（PSF）估计作为前提。对此，联合基于稀疏测度的PSF估计算法提出改进的ESGP算法。仿真结果表明，经改进的算法能够较好的复原天文图像。

天文图像；大气湍流；SGP；PSF估计

1 引言

地基光学望远镜对天文目标成像时，由于大气湍流引起的波前畸变，所获取的图像产生严重的降质，很难获得高分辨率的天文图像[1]，需要对天文图像进行复原。

天文图像的高清晰复原方法，主要分为两类：一类是针对成像环节，利用自适应光学（adaptive optics,AO）系统实时补偿大气湍流造成的影响，实现波前像差纠正[2]。但自适应光学仪器制造极其复杂，改进成本高；受硬件条件的限制，不可避免的存在误差。第二类方法是针对观测结果，通过图像复原技术来复原高分辨率图像。这类方法简单、易于实现且代价低，同时也可作为第一类方法的有效补充。因此，无论采取哪种方法，相应的图像复原后处理技术都是必不可少的[3]。

图像复原算法研究作为天文图像处理的一个重要方向，已取得了大量成果。在斑点成像技术方面，最早的有A.Labeyrie提出的斑点干涉测量算法[4]。之后，W.H.Richarson和L.B.Lucy分别相互独立的提出了基于Bayes原理的R-L算法[5]，R-L算法收敛速度较慢且需要知道点扩散函数为前提。Ayers和Dainty提出了迭代盲解卷积（Itertive Blind Deconvolution,IBD）算法[6]，其基本思想就是在空间域和Fourier域交替施加约束条件，最终得到理想目标图像的估计。但算法受样本初始值的影响大，缺乏可靠性，解的唯一性和收敛性不能得到有效保证。Deepa Kundar提出了基于非负性和有限支持域的递归迭代逆滤波算法（NAS-RIF)[7]。算法结构简单，且算法在凸集上进行迭代，解的唯一性和算法的收敛性都可以得到保证，取得了很好的效果。但由于算法构建的逆滤波器具有高通的性质，会导致高频噪声放大。Bonettini等利用高效的伸缩策略和步长更新规则提出了伸缩梯度投影算法[8]，该算法具有精度高，鲁棒性好的特点，同时由于利用了高效的伸缩策略和步长更新策略，相比常规梯度投影类迭代算法，其收敛速率大大提高。

SGP算法假定点扩散函数（PSF）是已知的，但实际情况下，PSF通常是未知的，这限制了SGP算法的应用。本文在伸缩梯度投影算法（SGP）基础之上，针对其需要较为精确的PSF估计为前提，联合基于稀疏测度的PSF估计算法提出改进的ESGP算法。首先，通过基于稀疏测度的PSF估计算法[10]估计出较为精确的PSF；然后，利用估计出来的PSF通过SGP算法对图像进行反卷积得到复原图像。

2 伸缩梯度投影算法（SGP）概述

其中，A是一个N×N的矩阵，指成像过程对清晰图像的物理影响，这里可理解为PSF。X是需要被复原的清晰图像，η指的是图像获取过程中的加性噪声，b指的是实际观测图像。图像盲复原问题即在除观测图像以外无任何先验知识的前提下，从观测图像b中得到清晰图像的近似x的过程，这是一个病态的问题。这类问题根据非负性和通量守恒的约束可以转化为极小值问题：

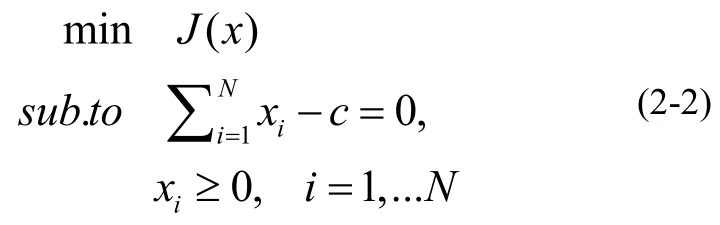
在SGP算法中，J(x)表示为Ax与b之间的K-L距离：

梯度类投影算法中，关键的一步就是投影的计算。投影算子的定义为：

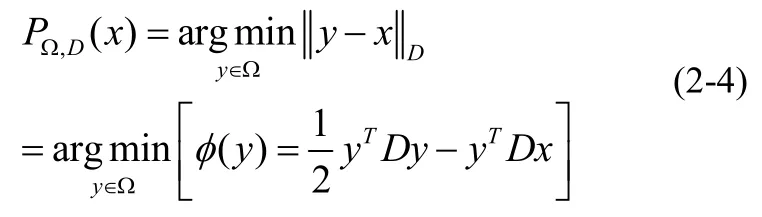
在SGP算法中，每次迭代中需要计算：

也就是说，必须解决如下的约束凸二次规划问题：

其中，

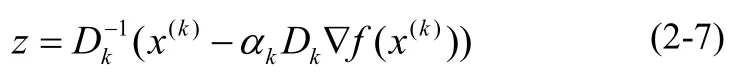
根据约束集的特殊结构，问题（2-6）可以表示为一维的寻根问题。

对于这种含非等式约束的情形，首先构造拉格朗日罚函数：

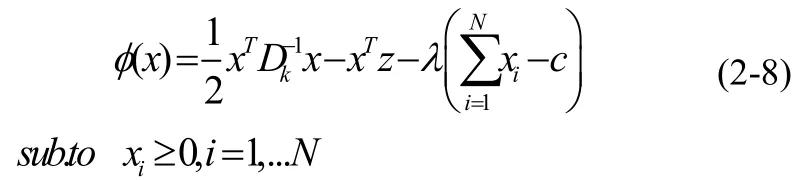
列出其KKT条件：

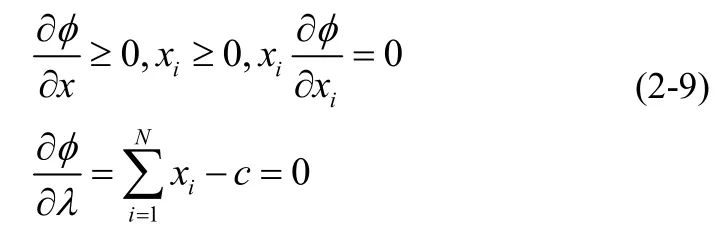
由上述KKT条件可得：

对于（2-11）这种分段线性单调非递增的求根问题，采用文献[11]中基于切割的方法可以高效的解决。

同比常规梯度投影类算法，SGP算法通过使用有效的步长和伸缩矩阵的更新策略使得收敛速率大大提高。同L-R算法相比，SGP算法在图像去模糊问题中得到与L-R算法相同复原精度的同时，所需的时间大大减少。

3 改进的图像盲复原算法ESGP

SGP算法在处理图像去模糊问题时是有非常有效的，但需要一个较为精确的PSF估计为前提。实际问题中，PSF往往是未知的，因此需要在仅已知观测图像的情况下估计出较为精确的PSF。

目前已有很多PSF的估计算法，总体上分为两类：第一类是利用图像的边缘估计模糊核[12,13,14]，这类算法估计图像的边缘并用模拟的块替换掉模糊图像的边缘，由此估计出模糊核。由于现实模糊图像中，需要被替换掉的复杂的纹理信息往往遭到严重的破坏，此类算法不稳定，甚至产生错误的模糊核。第二类算法充分利用了自然图像统计信息的先验知识，即它们的分布导数和模糊核是稀疏的、连续的。利用这些信息，此类算法通过最大后验概率的方法[15,16]或者简单的代价函数[10,17]来估计模糊核。其中，文献[10]中的基于稀疏测度的PSF估计算法相对简单，且复原效果好，适用于天文图像的复原。

图像复原问题是个病态问题，即在图像复原过程中由于噪声的存在导致复原的结果与真实图像相差甚远，解决图像复原病态问题的基本做法就是对解进行正则化约束[18-19]，来减少数据波动对解的影响，从而保证解的稳定性。

l1范数相对 l0范数具有更好的优化求解特性而广泛应用于表达信号的稀疏性，但是由于它的尺度可变性，简单的减小信号就会使l1范数变小。图像处理中，l1范数作用于高频部分，当图像中噪声增加时，相应的 l1范数会增大，因此减小l1范数可以有效地抑制噪声。而当图像的模糊度增加时，相应的l1范数会减小。因此，在图像去模糊中，简单的使用l1范数约束会产生模糊的图像。l1范数和 l2范数的比例 l1/l2是 l1范数的归一化，当它作用于图像高频部分时，图像模糊度的增加会导致两个范数同时减小，但 l2范数减小的更快，因此它们的比例会增大，这样l1/l2可作为图像模糊度的有效约束。

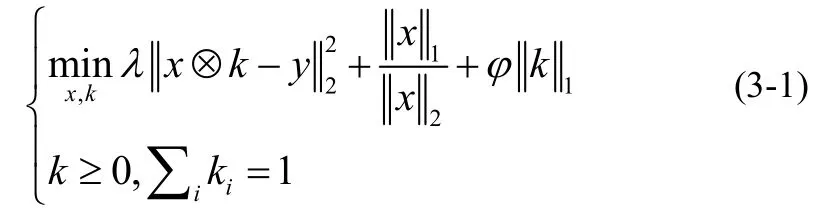
其中，x是未知的在高频空间的清晰图像，k是未知的模糊核，⊗是二维卷积算子。代价函数包含三个部分，第一部分是模型(3-1)的似然项。第二部分是一个 l1/l2正则项，它是l1的归一化版本，具有尺度不变性。第三部分，是对模糊核的k的l1范数的惩罚，以减少模糊核中的噪声。

式(3-3)是非凸的，解决方法是给x和k一个初始值，然后交替进行x和k的更新：

x更新的子问题可表示为：

k更新的子问题可表示为：

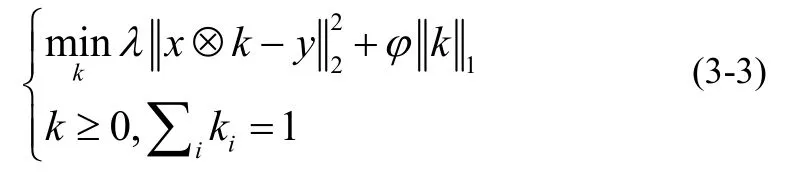
该问题可通过迭代重加权最小二乘算法[21]高效解决，其中k到约束集的投影即设定非零元素为0，并重新归一化。

仿真结果表明，该算法结构简单、效率高且能够较为精确的估计出PSF。

4 仿真结果与分析

为客观验证算法的恢复质量，本文采用峰值信噪比(Peak Signal to Noise Ratio,PSNR)、结构相似度(structural similarity)2个指标对复原结果进行比较。峰值信噪比主要用于来评价图像复原方法对噪声的影响，其值越大，说明图像受噪声影响越小。其定义为：

上述指标从统计意义上对图像进行分析，并不涉及信号自身的内容，没有考虑到像素之间的相关性。因此评价结果与人的主观感知不能取得完全一致。结构相似法 SSIM（structural similarity）是一种基于结构信息衡量原始信号与处理后信号之间相似程度的方法，与主观质量评价关联性较强，其值在0到1之间，越接近1说明与原始清晰图像越相似。

下面给出不同PSF估计对SGP算法的影响的仿真，将第一类算法中文献[13]中的算法和第二类算法中文献[15]中的算法仿真比较，结果如图1所示：

图1　不同PSF估计对SGP影响

表1　不同PSF估计下SGP复原指标

从复原图直观的可看出，文献[11]中的算法取得了更佳的效果，PSNR和SSIM指标也印证了这一点。

5 结束语

本文给出一种基于SGP算法改进的图像盲复原算法，鉴于SGP算法需要较为精确的PSF估计为前提，采用了基于稀疏测度的 PSF估计算法，该 PSF估计算法能较好的估计出PSF。仿真结果显示改进的算法能获得较好的恢复效果，具有很好的收敛性。

[1] Sheppard D G,Hunt B R,Marcellin M W.Iterative multiframe superresolution algorithms for atmospheric-turbunceegraded imagery[J].JOSA A,1998,15(4):978- 992.

[2] Jolissaint L,Carfantan H, Anterrieu E.Exploring the impact of PSF reconstruction errors on the reduction of astronomical adaptive optics based data[C]//SPIE Astronomical Telescopes+ Instrumentation.International Society for Optics and Photonics,2008.

[3] Schulz T J.Multiframe blind deconvolution of astronomical images[J].JOSA A,1993,10(5):1064-1073.

[4] Labeyrie A. Attainment of diffraction limited restoration in large telescopes by Fourier analyzing speckle patterns in star images[J]. Astron.&Astrophys,1970,(6):85-87.

[5] Lucy L B.An iterative technique for the rectification of observed distributions[J].The astronomical journal,1974, (79):745.

[6] Ayers G R,Dainty J C.Iterative blind deconvolution method and its applications[J].Optics letters,1988,13(7):547-549.

[7] Kundur D,Hatzinakos D.A novel blind deconvolution scheme for image restoration using recursive filtering[J]. Signal Processing,IEEE Transactions on,1998,46(2):375-390.

[8] Bonettini S,Zanella R,Zanni L. A scaled gradient projection method for constrained image deblurring[J].Inverse Problems,2009,25(1):125-130.

[9] Dabov K, Foi A,Katkovnik V,et al.Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering[J]. Image Processing,IEEE Transactions on,2007,(16):080-095.

[10] Krishnan D,Tay T,Fergus R.Blind deconvolution using a normalized sparsity measure[C].Computer Vision and Pattern Recognition (CVPR),2011 IEEE Conference on. IEEE,2011:233-240.

[11] Dai Y H, Fletcher R.New algorithms for singly linearly constrained quadratic programs subject to lower and upper bounds[J].Mathematical Programming,2006,106(3):403-421.

[12] Sun L,Cho S,Wang J,et al.Edge-based blur kernel estimation using patch priors[C]//Computational Photography (ICCP), 2013 IEEE International Conference on.IEEE, 2013:1-8.

[13] Cho T S, Paris S,Horn B K P,et al.Blur kernel estimation using the radon transform[C]//Computer Vision and Pattern Recognition(CVPR),2011 IEEE Conference on.IEEE,2011: 241-248.

[14] Joshi N, Szeliski R,Kriegman D.PSF estimation using sharp edgeprediction[C]//ComputerVisionandPattern Recognition,2008.CVPR 2008.IEEE Conference on.IEEE, 2008:1-8.

[15] Levin A,Weiss Y,Durand F,et al. Efficient marginal likelihood optimization in blind deconvolution[C]// Computer Vision and Pattern Recognition (CVPR),2011 IEEE Conference on.IEEE,2011:2657-2664.

[16] Levin A,Weiss Y,Durand F,et al.Understanding and evaluating blind deconvolution algorithms[C]//Computer Vision and Pattern Recognition, 2009.CVPR 2009.IEEE Conference on.IEEE,2009:1964-1971.

[17] Shan Q,Jia J,Agarwala A.High-quality motion deblurring from a single image[C]//ACM Transactions on Graphics (TOG).ACM,2008,27(3):73.

[18] Karayiannis N B,Venetsanopoulos A N.Regularization Theory in Image:the Regularizing Operator Approach[J]. Optical Engineering,1989,28(7):761-780.

[19] Karayiannis N B. Regularization Theory in Image Restoration-the Stablizing Functional Approach [J]. IEEE Trans on Acoustics,Speech and Signal Processing, 1990, 38(7):1155-1179.

[20] Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009, 2(1):183-202.

[21] Levin A, Fergus R, Durand F, et al. Image and depth from a conventional camera with a coded aperture[C]//ACM Transactions on Graphics (TOG).ACM, 2007,26(3):70.

[22] Buades A, Coll B, and Morel J M. A non-local algorithm for image denoising[J].Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San-Diego,2005,(2):60-65.

Application Of Scaled Gradient Projection Method In Telescopic Astronomical Image Restoration

In ground-based astronomy observations, due to the interference of atmospheric turbulence, the observed images are degraded, making it difficult to obtain high-resolution astronomical images, so astronomical image restoration is needed. The image deconvolution algorithm based on scaled gradient projection is highly effective with a high precision and a fast convergence, but requires an accurate point spread function (PSF) estimation as a prerequisite. Based on SGP, an enhanced SGP (ESGP) is proposed connected with the PSF estimation algorithm based on sparsity measure. Simulation results show that the improved algorithm gets brilliant performance on astronomical image restoration.

Astronomical image; atmospheric turbulence; SGP; PSF estimation

P11

A

1008-1151(2015)04-0008-03

2015-03-08

邵云龙（1988-），男，桂林电子科技大学在读生，研究方向为适用于天文观测的天文图像复原算法研究。