基于果蝇优化灰色神经网络的年电力负荷预测

傅军栋，刘 晶，喻 勇

（华东交通大学电气与电子工程学院，江西 南昌330013）

电力负荷预测水平已成为衡量电力系统运行管理现代化的标志之一［1］。它是制定发电计划和输电方案的主要依据，对合理安排机组启停、确定燃料供应计划、进行能量交易等具有重要意义，其预测精度的高低直接影响到电力系统运行的安全性、经济性。由于一些因素，如政治环境、人类活动和经济政策的复杂的和非线性的关系使得它非常难以准确预测年电力负荷。为提高电力负荷预测的准确性，学者和从业者提出了许多方法，如时间序列的技术和回归模型。然而，由于非线性拟合能力较差，这些预测方法难以实现较高的预测精度。近年来，许多人工智能的预测技术已在年电力负荷预测中应用，以提高预测的准确性。邵玉林［2］提出了一种基于粒子群优化方法的组合预测方法，它可以提高预测的稳定性和可靠性。夏非等［3］提出了采用径向基函数神经网络（RBFNN）中长期负荷预测模型，计算结果表明，该模型具有较高的预测精度和稳定性。Abou等［4］提出了人工神经网络（ANN）技术长期峰值负荷预测，这种基于埃及的电力网络历史数据的应用。贺晓等［5］提出了一种小波神经网络方法来预测中长期用电负荷，并且这种方法可以提高预测精度。李如琦等［6］提出了一种启发式支持向量机算法模型，并且该方法可以提供更准确的预测结果。这些方法从某种程度上都提高了电力负荷预测的精度。

拟采用果蝇优化算法［7］结合灰色神经网络的预测模型进行进行年电力负荷预测。

1 果蝇优化灰色神经网络（GNN-FOA）模型的预测方法

1.1 灰色神经网络（GNN）预测模型

灰色神经网络预测方法是灰色预测方法和人工神经网络方法相结合的算法［8］，即保留灰色预测方法中“累加生成”和“累减还原”运算，不再求参数，而是由BP神经网络［9-10］来建立预测模型和求解模型参数。

n个参数的灰色神经网络模型的微分方程式表达为

式中：y2，…，yn为系统输入参数；y1为系统输出参数；a，b1，b2，…，bn-1为微分方程式的系数。

利用这种灰色神经网络进行负荷预测的算法如下。

1）对电力负荷的原始数据序列进行“累加生成”运算，得到累加序列。

2）利用BP神经网络能够拟合任意函数的优势解决累加序列并非指数规律的问题。训练BP神经网络逼近累加数据序列Y。

3）利用现有已经训练好的BP神经网络进行预测，输出累加序列的预测值。

4）将累加数据的预测值进行“累减还原”运算，得到电力负荷的原始数据序列预测值。

1.2 果蝇优化算法（FOA）

果蝇优化算法（fruit fly optimization algorithm，FOA）是由潘文超教授于2011年提出的一种基于果蝇觅食行为推演出寻求全局优化的新方法［7］。这是一种交互式进化计算方法，通过模仿果蝇群体发现食物的行为，FOA能够达到全局最优。在实际中FOA已经被应用于许多领域，包括交通事件［11］，外贸出口预测［12］，模拟滤波器的设计［13］等。依照果蝇搜寻食物的特性，将其归纳为以下几个重要步骤。

1）参数初始化：FOA 的主要参数为最大迭代次数maxgen，种群规模sizepop，初始果蝇群的位置（X_axis，Y_axis）和随机飞行距离FR。

2）种群初始化：赋予果蝇个体利用嗅觉搜寻食物之随机方向与距离。

3）种群评价：首先，由于无法得知食物的位置，需要计算果蝇到原点的距离（Dist）。再计算气味浓度判定值（S）此值为距离的倒数。通过将气味浓度判断值（S）代入气味浓度判断函数（或称为适应度函数），求出果蝇个体位置的气味浓度（Smell）。并找出群体中气味浓度值最大的果蝇个体。

4）选择操作：保留最大气味浓度值和x、y坐标，此时，果蝇通过视觉飞往的最大浓度值的位置。进入迭代寻优，重复实施步骤2）～3），并判断味道浓度是否优于前一迭代味道浓度，若是则执行步骤4）。若味道浓度不再优于先前迭代的味道浓度值，或迭代次数达到最大，循环结束。

1.3 GNN-FOA预测模型

GNN-FOA预测模型的程序结构框图如图1所示。采用果蝇优化算法（FOA）为灰色神经网络（GNN）模型参数a，b1和b2进行迭代动态微调，使模型侦测能力提高，并获得最佳的GNN模型参数以进行预测。详情如下。

1）参数初始化。在果蝇优化算法的参数设定上，随机初始化果蝇群体位置区间X_axis，Y_axis∈[-50,50]，迭代的果蝇寻食的随机飞行距离区间FR∈[-10,10]，种群规模sizepop=20，而迭代次数maxgen=100。

2）初始进化。设置初始迭代次数为0，设定果蝇个体i寻食随机飞行方向rand()和飞行距离。其中rand()表示任意值产生函数。在GNN-FOA程序中，使用两个变量[X(i,:),Y(i,:)]来描述果蝇个体i的飞行距离。分别设

3）初步计算和数据预处理。计算果蝇个体i距离原点的距离Disti和气味浓度判断值Si。其中

在GNN-FOA程序中，使用D(i,1),D(i,2),D(i,3)来表示Disti，用(S(i,1),S(i,2),S(i,3))表示Si。将Si输入到GNN 预测模型进行年电力负荷预测。在GNN-FOA 程序中，参数a，b1和b2由(S(i,1),S(i,2),S(i,3))表示，分别设

通过年负荷预测结果，气味浓度值Smelli（或称为适应度函数）便可计算出来。该气味浓度Smelli通过均方差（RMSE）来表征网络输出预测值与实际值之间的误差。

4）产生种群后代。种群后代通过果蝇算法步骤2）～3）生成，然后输入到GNN模型中，重新计算气味浓度值，迭代加一，置gen=gen+1。

5）循环结束。当达到最大迭代次数时，停止条件满足，并获得GNN模型的最佳参数。若否，则返回执行步骤2）。

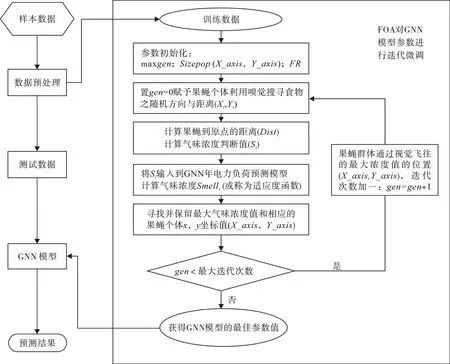
图1 GNN-FOA预测模型的程序结构图Fig.1 Diagram of the procedure structure of the GNN-FOA forecasting model

2 算例仿真

2.1 样本数据预处理

样本数据选自中国1987—2011年的年用电量［14］，如表1所示。在计算之前，需要对样本数据进行归一化处理，用下式使得样本数据统一规范在0～1的范围内。

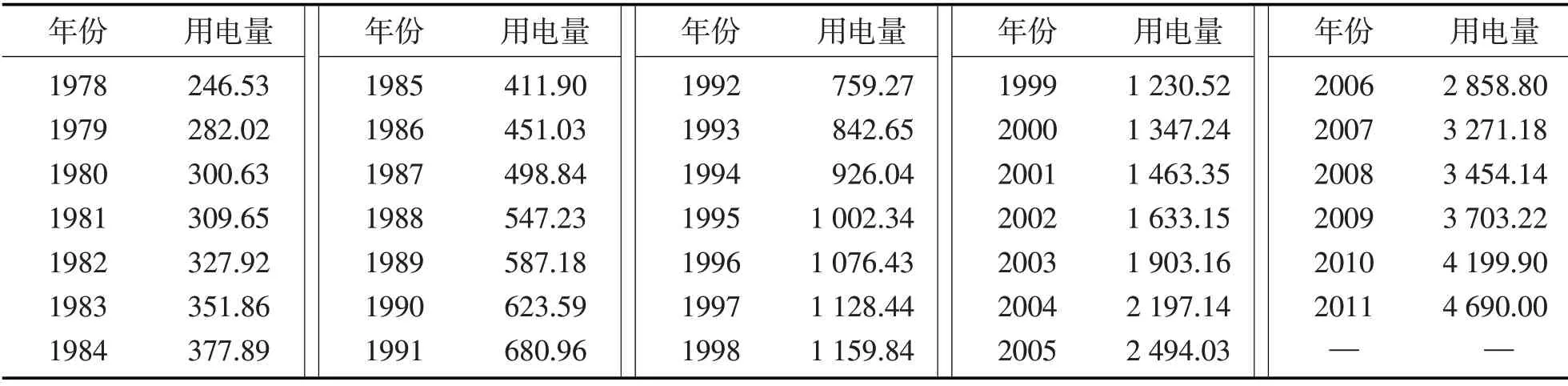
表1 中国1987—2011年年用电量Tab.1 Annual electricity consumption of China from 1978 to 2011 109 kWh

2.2 比较模型的选择

选定几种其他电力负荷预测模型的年电力负荷预测结果来比较。从表1中，可以看出，每年的电力负荷呈近似线性上升的趋势。因此，选择回归模型、GNN 模型、LSSVM 模型和广义回归神经网络（GRNN）模型与GNN-FOA预测模型做比较。GRNN是一种基于核回归标准统计方法的径向基函数（RBF）神经网络，在性能上，它具有优异的逼近能力和学习速度。在GRNN模型中只有一个参数需要确定。

实验环境包括Matlab2010a，GRNN工具箱，自行编写的MATLAB程序和英特尔（R）酷睿（TM）i3-380M的CPU、2 GB内存、320 GB硬盘和Windows 7旗舰版操作系统的计算机。

2.3 FOA为GNN模型确定的参数结果

在GNN-FOA 模型中，GNN 模型的3 个参数值由FOA 动态调整。如图2所示是参数优化的果蝇群体飞行路线。可以看到，果蝇群体飞行路线是相对平稳的，而且果蝇群体是直线飞行至食物位置的。因此，果蝇群体能快速而准确地寻找到食物的位置。GNN-FOA 在搜索最佳参数时的迭代均方根误差（RMSE）如图3所示。

经过100 代迭代寻优，可以看出，在25 代坐标为（728，747）处收敛，此时参数a、b1和b2最优值均为0.302 9。

图2 果蝇群体参数寻优飞行路线图Fig.2 The fruit fly swarm flying route for parameter optimization

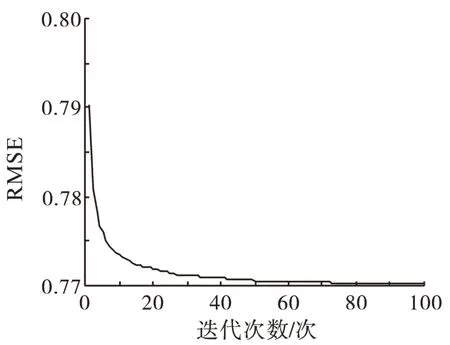
图3 GNN-FOA模型寻最佳参数的均方根误差Fig.3 The iterative RMSE trend of the GNN-FOA model in search of optimal parameters

2.4 预测结果与分析

根据FOA算法调整GNN模型参数的结果，a、b1和b2均被选定为0.302 9。在GNN模型中，参数a、b1和b2分别为0.503 7，0.526 4和0.528 3。在LSSVM 模型中，参数σ和C分别为5和10。其中，σ为核函数参数；C为惩罚因子。在GRNN模型中，参数σ为0.2。其中，σ为光滑因子。

GNN-FOA，GNN，LSSVM，GRNN和回归模型的数据训练的时间是分别为9，6，13，14 s和8 s。这5个模型在训练数据的处理上，训练时间是不同的。GNN-FOA模型与另外4个模型相比，需要每一代都调整一次参数。但是，在训练时间上，GNN-FOA模型仍具有极快的速度，它比GRNN模型快了5 s。

表2中列出了GNN-FOA，GNN，LSSVM，GRNN 和回归模型的年电力负荷预测结果。这5 中模型预测结果的相对误差如图4所示。从表2和图4中可以获取这5种预测模型的预测结果与实际值之间的误差。一般，最大相对误差是否在［-3%，+3%］和最小相对误差是否在［-1%，1%］的范围内是评价一个预测模型的标准。首先，GNN-FOA模型年电力负荷预测点的相对误差均在［-3%，3%］范围内，并且最大和最小相对误差分别为2008年的2.72%，和2009年的-0.727%。GNN模型有1个预测点的相对误差超出了［-3%，3%］的范围，即2008年的3.195%。有1 个预测点的相对误差即2007年的-0.98%在［-1%，1%］的范围之内。LSSVM 模型有2 个预测点的相对误差超过［-3%，3%］的范围，即2008年的3.13%和2009年4.412%。 所有预测点的相对误差均超过［-1%，1%］，其中最大相对误差为2009年4.412%，最小相对误差为2011年-1.863%。GRNN 模型有3 个预测点的相对误差超过［-3%，3%］，即2006年3.355%、2007年3.664%。664%、2009年3.509%，所有预测点的相对误差均超过［-1%，1%］。回归模型有4 个预测点的相对误差超过［-3%，3%］，即2008年7.354%，2009年3.017%，2010年-3.11%，2011年3.477%。仅有一个预测点的相对误差在［-1%，1%］内，即2007年-0.410%。其中回归模型2008年的相对误差7.354%是5 个模型所有预测点相对误差中最大的点。

表2 GNN-FOA，GNN，LSSVM，GRNN和回归模型的预测结果Tab.2 Forecasting results of GNN-FOA，single GNN，LSSVM，GRNN and regression model 109 kWh

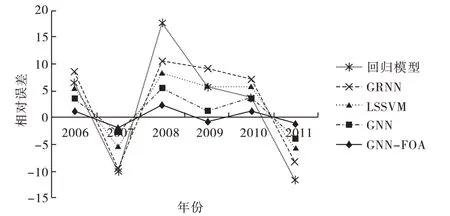
图4 GNN-FOA，GNN，LSSVM，GRNN和回归模型预测结果的相对误差Fig.4 The relative errors of the forecasting results for different forecasting models

在此，采用平均绝对百分比误差（MAPE），均方差（MSE）和平均绝对误差（AAE）来评估不同预测模型的预测能力［15］。

5种模型的平均绝对百分比误差（MAPE），均方差（MSE）和平均绝对误差（AAE）的比较如表3所示。可以看出，与另外4个模型相比，GNN-FOA模型的MAPE，MSE和AAE值要小得多，预测性能更佳。回归模型的MAPE，MSE 和AAE 值最大，预测精度最低，非线性拟合能力较差。与GRNN 模型相比，LSSVM 模型的MAPE值较小，MSE和AAE值却较大。因此，此处无法确定这两个模型在年电力负荷预测方面孰优孰劣。

表3 GNN-FOA，GNN，LSSVM，GRNN和回归模型的MAPE，MSE和AAE值Tab.3 The values of MAPE，MSE and AAE for GNN-FOA，single GNN，LSSVM，GRNN and regression model

综上，GNN-FOA 模型极大地缩小了预测值与实际值之间的差距，在年电力负荷预测问题中性能优于GNN、LSSVM、GRNN和回归模型。

3 结束语

随着“坚强智能电网”的建设和分布式可再生能源带来的发电容量的不断增加，准确的电力负荷预测能有效指导中国能源政策的重要实现。然而，年电力负荷与其影响因素的非线性关系使得电力负荷的预测变得复杂。因此，如何提高年电力负荷的预测准确性是值得研究的。GNN已广泛应用于实际各种领域，GNN已广泛应用于实际各种领域，果蝇优化算法（FOA）是一种新型的易于理解的群智能算法。与其他启发式算法相比，它大大缩短了程序代码并能迅速达到全局最优。文中用结合了GNN 和FOA 的GNN-FOA模型来预测年电力负荷。为验证所提出的方法，将GNN-FOA模型与GNN，LSSVM，GRNN和回归模型进行比较预测。结果表明，GNN-FOA 与其他替代预测模型在年电历负荷预测精度方面拥有显著优势，该算法是可行的。

[1] 史杰.负荷预测对电网安全运行的重要性[J].企业改革与管理,2014(5):109.

[2] 邵玉林.改进粒子群算法在电力负荷组合预测中的应用研究[D].衡阳:南华大学,2013.

[3] 夏非,范莉,苏浩益.基于粗糙集理论和启发式径向基函数神经网络的中长期电力负荷预测模型[J].电力系统保护与控制,2012(16):21-26.

[4] ABOU EL-ELA A.A Long-term load forecasting and economical operation of wind farms for Egyptian electrical network[J].Electr Power Syst Res.2009,79:1032-1037.

[5] 贺晓,刘爱国,孙蕾,等.基于小波神经网络的中长期电力负荷预测[J].陕西电力,2012(2):4-8+22.

[6] 李如琦,苏浩益,王宗耀,等.应用启发式最小二乘支持向量机的中长期电力负荷预测[J].电网技术,2011(11):195-199.

[7] PAN W T.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based System,2012,26(1):69-74.

[8] 程鹏,韦雅君,李金颖,等.基于改进的并联灰色神经网络模型在电力需求预测中的应用[J].广东电力,2011,24(8):13-16.

[9] 黄招娣,应宛月,余立琴,等.基于PSO的神经网络优化证券投资组合方法研究[J].华东交通大学学报,2013,30(2):42-46.

[10] 张利华,马钧钊,勒国庆,等.基于BP神经网络的仓储烟草霉变预测[J].华东交通大学学报,2013,30(3):13-16.

[11] 史亚东,陆健,陆林军.基于RFID技术和FOA-GRNN 理论的高速公路道路关闭交通事件对车辆影响的判断模型[J].武汉理工大学学报,2012,34(3):63-68.

[12] 许智慧,王福林,孙丹丹.基于FOA-RBF神经网络的外贸出口预测[J].数学的实践与认识,2012,42(13):16-21.

[13] 肖正安.基于果蝇优化算法的模拟滤波器设计[J].湖北第二师范学院学报,2012,29(2):26-29.

[14] 中国国家统计局.中国能源统计年鉴2011[M].北京:中国统计出版社,2011.

[15] 陈昊,王玉荣.一种负荷预测模型预测能力的评价标准[J].电力需求侧管理,2010(6):24-26.