BP神经网络在解决电力消耗问题中的应用

傅军栋，喻 勇，黎 丹

（华东交通大学电气与电子工程学院，江西 南昌330013）

电力工业是国民经济发展中最重要的基础能源产业，是国民经济的第一基础产业和关系国计民生的基础产业。但现阶段江西电力的供给与需求很难达到平衡，比如1999年江西电力生产比上年增长8.90%，而电力消费只比上年增长3.35%。再比如2008年江西电力生产比上年增长-1.21%，呈现负增长，而电力消费只比上年增长6.37%。出现能源的浪费或出现电力供应不足现象。如何提高电力系统负荷平衡预测精度一直是国内外学者所关注的热点问题。神经网络高度的自学习、自组织和自适应能力，以及其自身的非线性，使其不需要知道具体的精确数学模型，只需用神经网络就能逼近系统输入和输出之间的非线性。因此，神经网络被广泛的应用于各领域的预测模型中。

1 BP神经网络

BP神经网络是一种多层前馈神经网络，该网络的主要特点是信号前向传递，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阀值，从而使BP神经网络的预测输出能够不断地逼近期望输出。

简单的说神经网络原理就是利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差，如此一层一层的反传下去，就获得了所有其他各层的误差估计。BP神经网络的结构图如图1所示。

BP 算法的核心是数学中的“负梯度下降”理论，即BP 网络的误差调整方向总是沿着误差下降最快的方向进行，常规三层BP 网络权值和阀值调整公式如下：

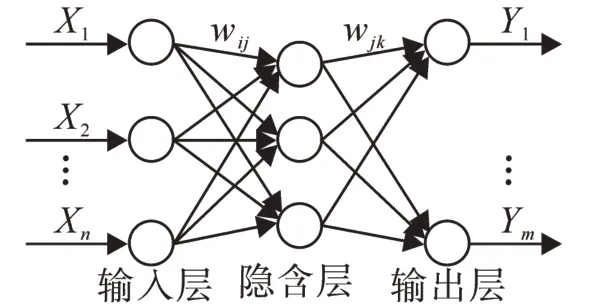
图1 BP神经网络的结构图Fig.1 BP neural network structure

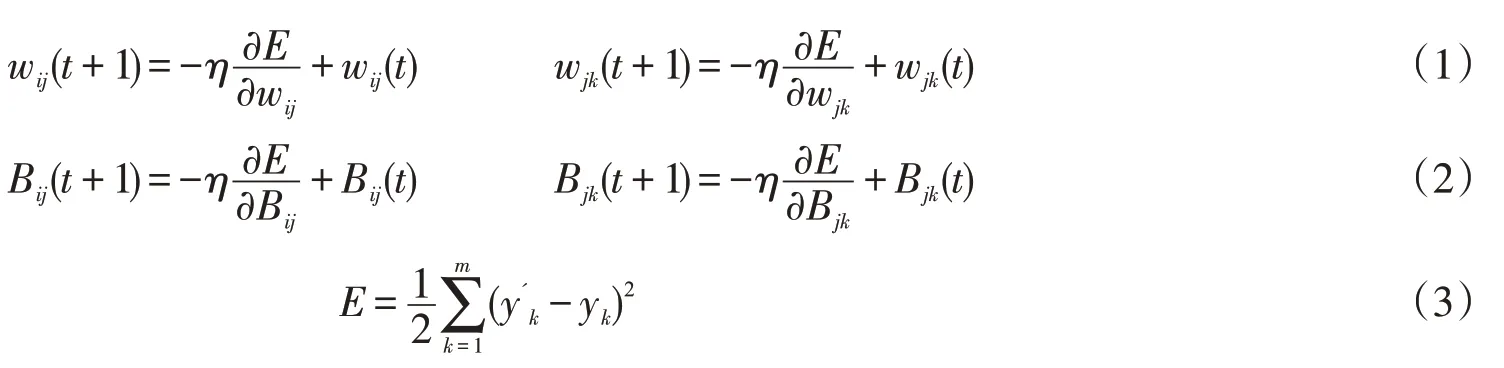
其中，E为网络输出与实际输出yk样本之间的误差平方和即误差函数，神经网络每一次学习训练之后，都要进行学习结果的判别。判别的目的在于检查输出的误差是否满足允许的标准；η为网络的权值调整幅度。wij(t)为t时刻输入层第i个神经元与隐含层第j个神经元之间的权值即连接强度系数；wjk(t)为t时刻隐含层第j个神经元与输出层第k个神经元之间的权值；B为神经元的阀值，下标的意义同上。图2为BP网络按有导师学习方式进行训练的流程图。

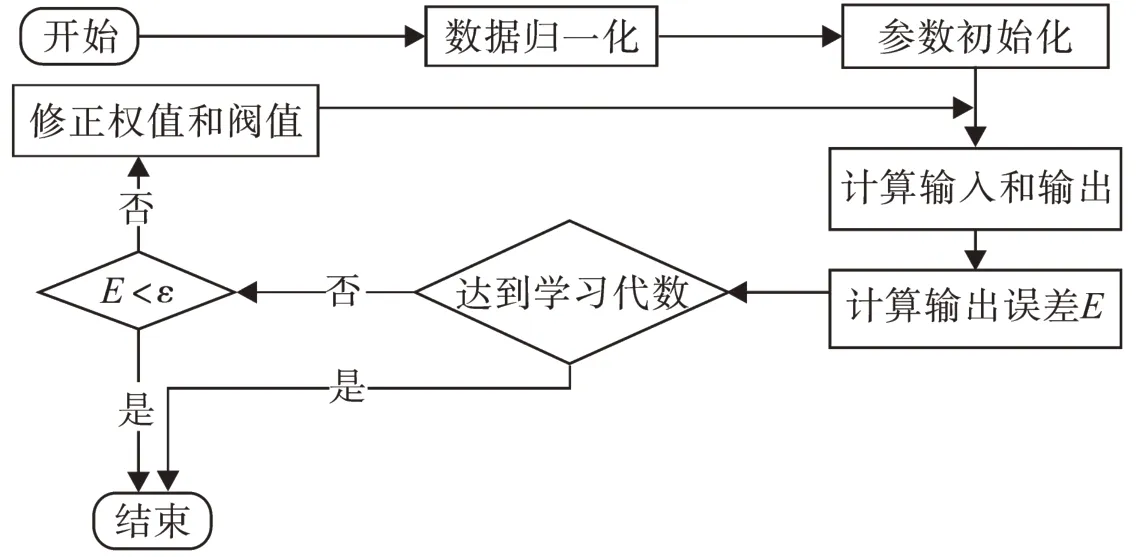
图2 流程图Fig.2 Flow diagram

2 模型分析

影响电力的需求因素有很多，主要考虑人口、居民消费水平、第一、二、三产业总值、人均地区生产总值6个因素对电力需求的影响作出相应的预测。表1为江西1991—2011年21年间人口、居民消费、第一、二、三产业总值、人均地区生产总值以及用电情况统计表。

本案例解决两个问题：

问题一：由于数据有限，将1991—2009年和2010—2011年数据作为模型的训练和测试样本，以1978，1980，1985，1990年对应的人口、消费水平、产业产值等数据为预测输入对各年耗电量进行预测，也可根据“十二五”规划提供的数据来预测未来耗电量。

问题二：根据以上提供的数据，利用传统多元回归模型得出多元线性回归方程，利用所得方程对耗电量进行预测。

2.1 问题一分析

2.1.1 网络结构确定

根据表1可知，输入层神经元有6个，而输出层神经元个数为1个。根据Kolmogrov定理，隐含层采用13个神经元。

网络采用net=newff（dx，［6，13，1］，｛’tansig’，’tansig’，’purelin’｝，’taningdx’），其中dx=［-4，4］；其他参数如下：轮回次数net.trainParam.show=1000；学习速率net.trainParam.Lr=0.1；最大训练次数net.trainParam.epochs=10 000；误差net.trainParam.goal=0.5*10^（-4）。

根据系统输入输出（X，Y）确定网络输入层节点数n，隐含层节点数l，输出节点数m，初始化连接权值wij、wjk和阀值a、b。隐含层输出H采用tansig算法。

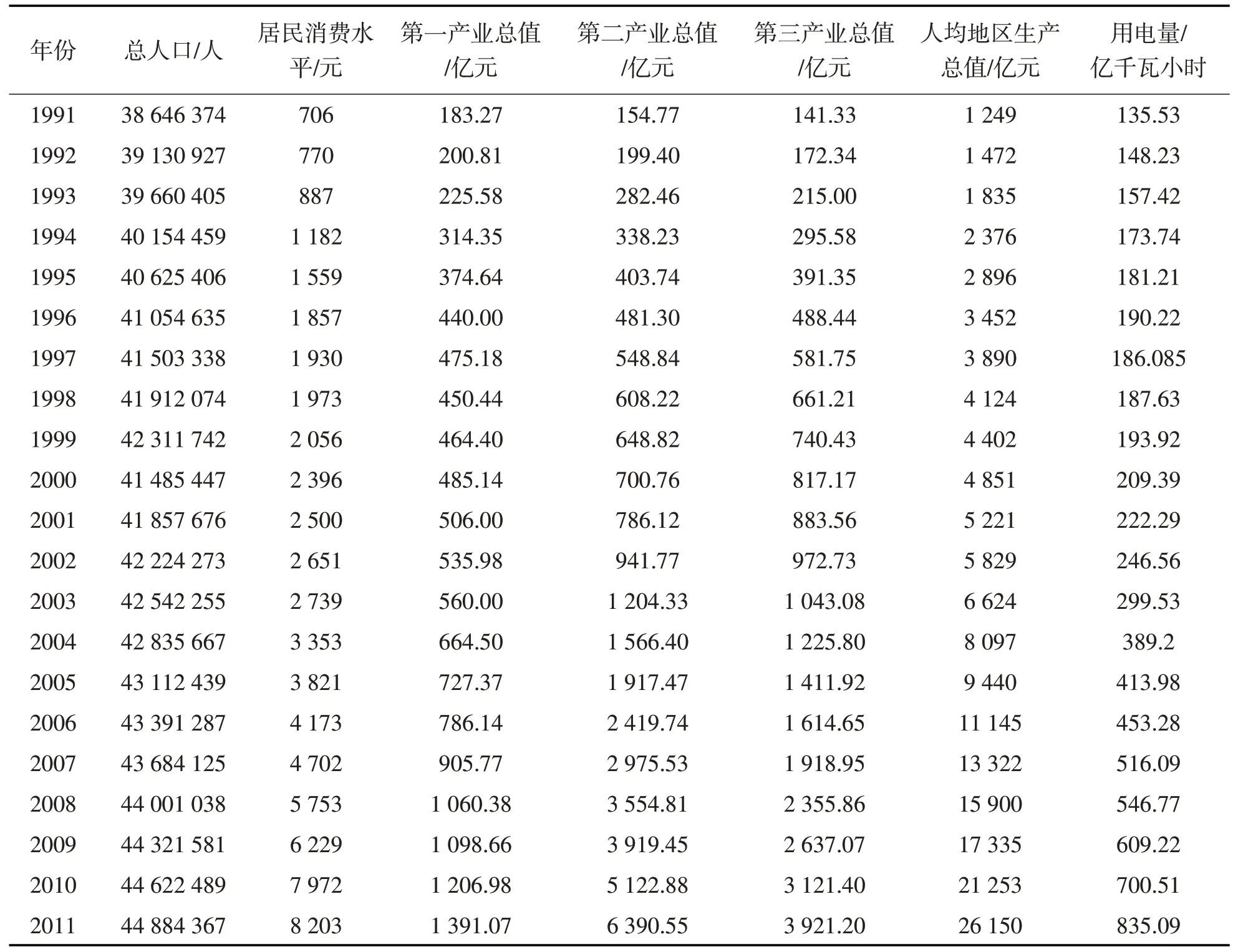
表1 数据统计Tab.1 Statistics

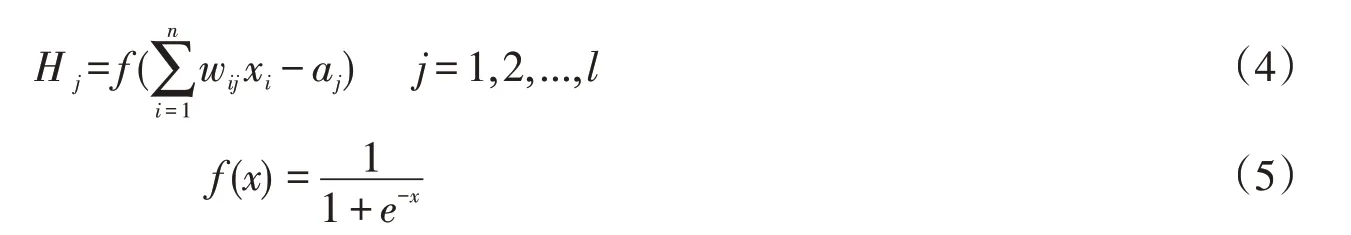
输出层输出计算采用purelin算法。神经网络预测输出。

为了避免奇异样本对网络的影响，因此，需要将数据转化到同一等级的数据，将每组数据都变为-1～1之间的数，采用函数premnmx对数据样本进行，处理，这个函数使用的算法是

式中：p为输入矩阵即原始没有处理过的数据；pn为标准化的输入矩阵即归一化之后的数据；minp，maxp分别为各输入样本对应的最小和最大值。

2.1.2 网络训练与测试

问题一是为了通过已有数据（1991—2011年）预测历史遗失数据（1978，1980，1985，1990）年用电量，表2为需要预测年份的已知的6个参数。

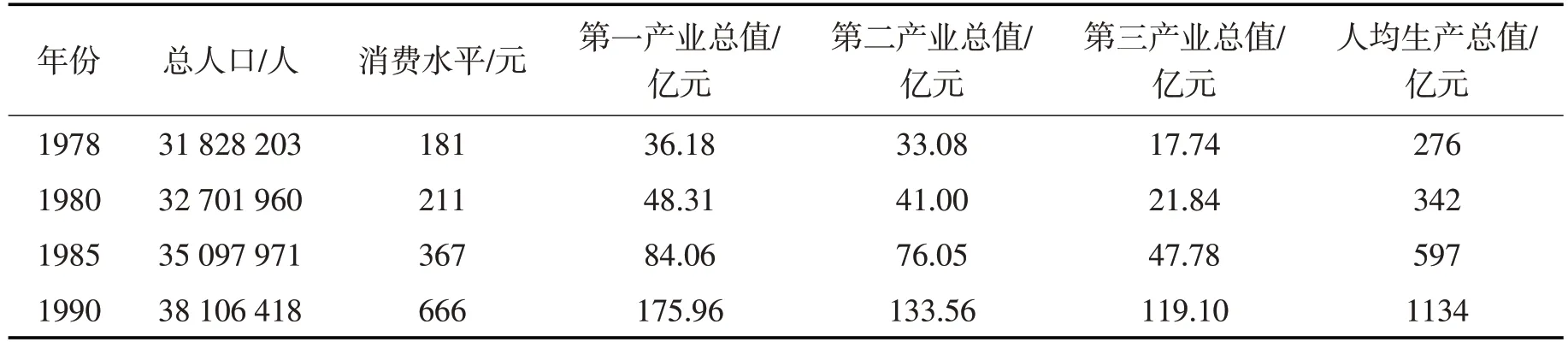
表2 预测年份参数Tab.2 Prediction parameters

图3为在Matlab2009中经过训练之后得到的训练样本的误差曲线，左图为训练样本误差曲线，右图为测试样本误差曲线。

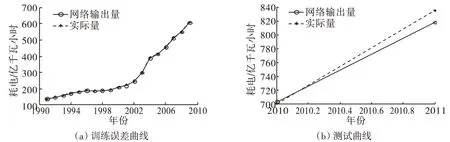
图3 模型一训练、测试误差曲线Fig.3 Error curve of the first model

表3 测试样本对比Tab.3 Comparison chart

表4 预测结果Tab.4 Prediction results

从表3中，可以看出网络输出的结果与实际值非常接近，再将历史资料数据输入训练网络中对历史耗电量进行预测，预测结果如图4所示。通过中华人民共和国国家统计局网站只查阅到1990年的数据，数据显示1990年江西耗电量为127.65亿千瓦小时，对比于神经网络得到的结果，可以看出误差还是在一个很小的范围，证明BP神经网络在电力消耗中的应用是可行的。

2.2 问题二分析

2.2.1 多元线性回归方程模型

假设因变量Y与自变量X1,X1,...,Xm间存在如下关系：

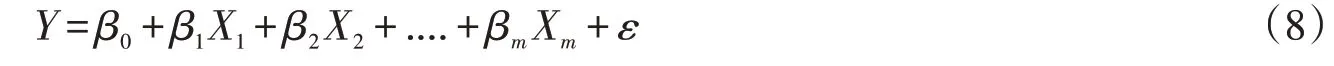
式中，β0是常数项，β1,β2,...,βm称为偏回归系数。βi(i=1,2,...,m)的含义为在其他自变量保持不变的条件下，自变量Xi改变一个单位时因变量Y的平均该变量。ε为随机误差，也叫残差。它表示Y的变化中不能由自变量Xi(i=1,2,...,m)解释的部分。

模型的参数估算采用最小二乘法求得，对于随机抽取的n组值(Yi,Xji)，如果样本函数的参数估计值已经得到，则有：

根据最小二乘原理，参数估计值应该是下列方程组的解

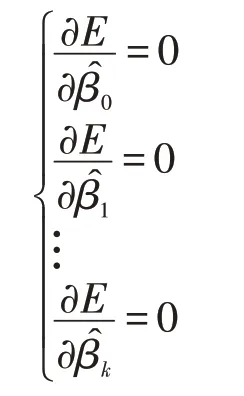
得到（k+1）个正规方程组，解该线性方程组，即可得到（k+1）个待估参数的估计值,j=0,1,2,...,k。

同样跟模型一类似，采用1991—2009年的数据作为回归模型的样本，2010和2011年的样本作为检测样本。可以得到：

β0=-1 011.09；β1=2.92×10-5；β2=0.148 786；β3=-1.039 46；β4=-0.182 54；β5=-0.684 95；β6=0.176 036；

所以Y=-1 011.09+2.92×10-5X1+0.1487 86X2-1.039 46X3-0.182 54X4-0.684 95X5+0.176 036X6。

3 结果分析

根据以上得到的参数估计值可得：

表5 检测样本结果对比Tab.5 Comparison results of test samples

图4为两种方法结果对比图。

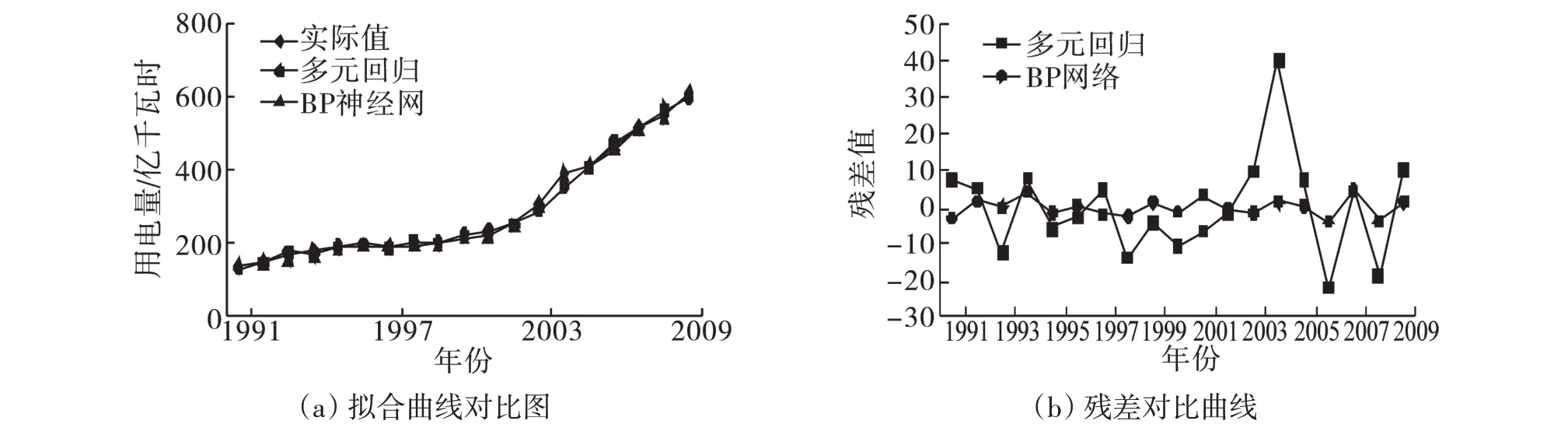
图4 两个模型对比图Fig.4 Comparison chart of two models

可以看出，总体来说BP 神经网络的收敛性较好，因此，利用神经网络对电能进行预测有较高的精准度。因为BP神经网络在学习训练过程中能够根据各影响因素对总耗电量演变趋势所起作用的大小自动权重调节，而传统的多元回归法由于线性假设，导致某些影响因素在分析过程中很明显违背常理，比如β3,β4,β5都为负数，它们分别为第一、第二、第三产业总值，说明这些值越大耗电量反而越少，这很明显的违背常理，所以不建议采用传统方法来预测耗电量。结合2012年的相关数据，可以得到2012年的网络预测耗电量为862.351 2 亿千瓦小时。而根据江西统计局提供的数据，2012年的实际用电量为867.7亿千瓦小时，而发电量达1374.1亿千瓦小时，可见预测误差很小，如果能够很好把握用电量多少，那么就可以避免不必要的浪费。

4 结束语

以上分析表明，BP神经网络能够较好地预测非线性条件下的电力消耗问题，并且其预测精度与传统多元回归分析方法相比有一定提高，收敛性更好。可为江西电力消耗量的预测提供了一种新颖、有效的解决办法，对供电部门具有一定的参考价值。

[1]黄招娣,应宛月,余立琴,等.基于PSO的神经网络优化证券投资组合方法研究[J].华东交通大学学报,2013,30(2):42-46.

[2]蒋惠凤,何有世,张兵,等.基于BP神经网络的江苏用电量预测模型研究[J].统计与决策,2005(1):46-48.

[3]黄海萍.基于BP神经网络的中国电力需求预测[J].科学技术与工程,2007,7(4):612-616.

[4]尹春华,陈雷.基于BP神经网络人口预测模型的研究与应用[J].人口学刊,2005(2):44-48.

[5]蒋建平,章杨松,阎长虹,等,BP神经网络在地基土压缩指数预测中的应用[J].中南大学学报:自然科学版,2010,42(2):722-727.

[6]葛彩莲,蔡焕杰,王健,等.基于BP神经网络的降雨量预测研究[J].节水灌溉,2010(11):7-10.

[7]李湘梅,周敬宣.基于BP 神经网络的城市总生态足迹预测研究——以武汉市为例[J].环境科学与技术,2007,8(30):68-70.

[8]蒋建平,章杨松,阎长虹,等.BP神经网络在地基土压缩指数预测中的应用[J].中南大学学报:自然科学版,2010,2(41):722-727.

[9]王野平,陈文倩,江华荣.基于BP算法的中密度纤维板热压机压力控制研究[J].华东交通大学学报,2012,29(4):29-34.

[10]郭杰,欧名豪,刘琼,等.基于BP神经网络的南通市建设用地需求预测[J].资源科学,2009,31(8):1355-1361.

[11]张旭东.基于BP神经网络的纳卫星轨道温度预测[J].北京航空航天大学学报,2008,12(34):1423-1427.

[12]师彪,李郁侠,于新花,等.动态调整蚁群-BP神经网络模型在短期负荷预测中的应用[J].水利发电学报,2011,3(30):5-9.

[13]张利华,马钧钊,勒国庆,等.基于BP神经网络的仓储烟草霉变预测[J].华东交通大学学报,2013,30(3):71-75.

[14]黄招娣,应宛月,余立琴,等.基于PSO的神经网络优化证券投资组合方法研究[J].华东交通大学学报,2013,30(2):42-46.