某高层建筑风荷载体型系数数值模拟分析

吴华英，李 婷，江 涛，黄 宏

（1.江西杭萧钢构有限公司，江西 南昌330013；2.华东交通大学土木建筑学院，江西 南昌330013）

随着我国经济的快速发展及人口数量的增加，各地高层建筑物愈来愈多，当高层建筑群的间距较近时，由于漩涡的相互干扰，建筑物局部风压会显著增大。现行的《建筑结构荷载规范》（GB50009-2012）（以下简称《荷规》）只给出了较为规则建筑物的风载体型系数，而对于体型复杂的建筑物以及建筑群，应进行风洞试验或者数值模拟以确定其风载体型系数［1］。与风洞试验相比，采用数值模拟分析进行抗风研究具有耗费时间少，模型的形状和尺寸不受限制，成本经济等优点。

目前已有学者对群体建筑物风荷载影响进行了数值模拟研究，杨伟［2］对两栋方形高层建筑模型在串列、并列和偏置状态下的静态三维流场和风荷载进行了计算。沈祺［3］对上海市某住宅小区风场进行了三维数值模拟研究，讨论了街区群楼间间距及建筑布局等因素改变时对风场和风荷载的影响。张敏［4］对由4栋高层建筑组成的建筑群风荷载和风场进行了数值模拟研究。郑朝荣［5］对某发电厂景观烟囱的风载体型系数进行了数值模拟计算。曲文超［6］对两个相邻建筑物风荷载干扰效应的静、动力风荷载进行了数值模拟分析。吴剑锋［7］对正方形平面封闭式房屋的风荷载体型系数进行了数值模拟计算。赵鹏抟［8］对通信塔风压体型系数进行了模拟计算。

1 工程概况

南昌“云中城”项目位于南昌市高新区艾溪湖大桥东，地块西临艾溪湖、南临紫阳大道。该项目包括2栋51层223.5 m 高的塔楼、1栋3层23.75 m 高的裙楼和1栋2层13.45 m 高的商业建筑。其中2栋塔楼总建筑面积318 738 m2（包括地上、地下），地上总建筑面积216 293 m2，地下3 层（局部4 层）主要为车库和设备用房。裙楼总建筑面积8 321 m2，商业建筑总建筑面积1 556 m2，项目效果图如图1。2栋塔楼地下4层为型钢混凝土框架-混凝土核心筒结构体系，地上结构采用钢管混凝土柱［9］+钢梁框架-混凝土核心筒结构体系。

图1 项目效果图Fig.1 The project renderings

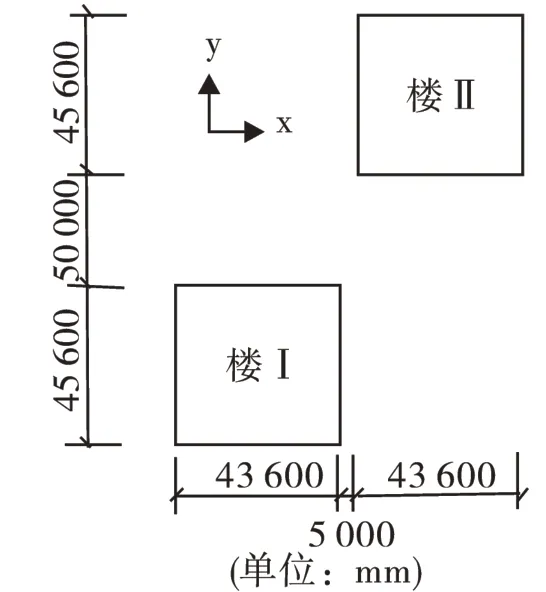
图2 办公楼平面布置图Fig.2 Plane layout of the project

项目中2栋塔楼高度为223.5 m，为超高层建筑。该类建筑结构对风荷载的作用极为敏感，且2座塔楼的间距仅50 m。预计流经这个垂直方向狭窄通风道的气流有别于简单塔状建筑物的周围气流，双塔间漩涡的相互干扰效应将使建筑物的某些部位局部风压显著增大，群体效应对建筑物和建筑物之间的通道也会造成危害。为保证办公塔楼结构和幕墙设计的安全、经济、合理，同时按照国家建筑结构荷载规范的建议，有必要对其结构表面风压和体型系数进行测定。综合多方面因素考虑，将采用数值模拟方法对办公塔楼的表面风压进行分析研究。

在上述学者的研究基础上，以下将采用软件FLUENT14.0对项目中建筑物风荷载作用进行数值模拟分析。

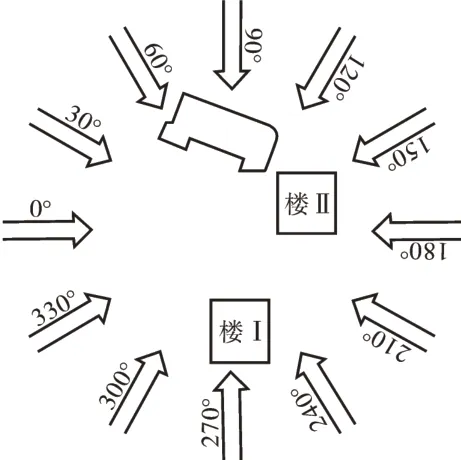
图3 风向角示意图Fig.3 The wind azimuths

2 数值模拟

项目中建筑物风荷载数值模拟的主要技术参数为：根据《荷规》，50年一遇的基本风压为0.45 kN·m-2，项目所在地的地面粗糙度为B类，地貌粗糙指数α=0.16。计算时在0°～360°范围内每隔30°取一个风向角，共有12个风向角工况，风向角如图3。

2.1 模型建立

采用ICEM CFD14.0作为前处理软件，塔楼和裙楼按原型尺寸建立几何模型，可以避免尺寸效应对计算结果产生的影响，同时考虑周围建筑物对风场的影响。模拟中采用的流域大小（长×宽×高）为3 600 m×2 500 m×800 m，在长度方向模型置于流场1/3处，阻塞率小于2%。由于分析结构较为复杂，模型计算区域采用非结构的四面体网格划分方法，在靠近办公塔楼表面采用加密的网格形式。网格尺寸由内向外逐渐增大，在靠近建筑物表面区域，使用过渡的棱柱体网络（6 层），整个流域总的网格数约为430万个，网格示意图如图4、图5。

图4 0°整体网格示意图Fig.4 The whole mesh scheme of 0°

图5 办公塔楼局部网格示意图Fig.5 Local mesh scheme of building

模拟中采用CFD常用的标准k-ε湍流模型配合非平衡壁面函数法进行模拟计算，该方法可以较为精确的模拟钝体绕流问题。因可实现的k-ε湍流模型一般只适用于湍流的核心区域，而在近壁面，湍流流动受到显著影响，故模型采用非平衡壁面函数法来处理近壁面的湍流状态。

标准k-ε湍流模型控制方程为［10］：

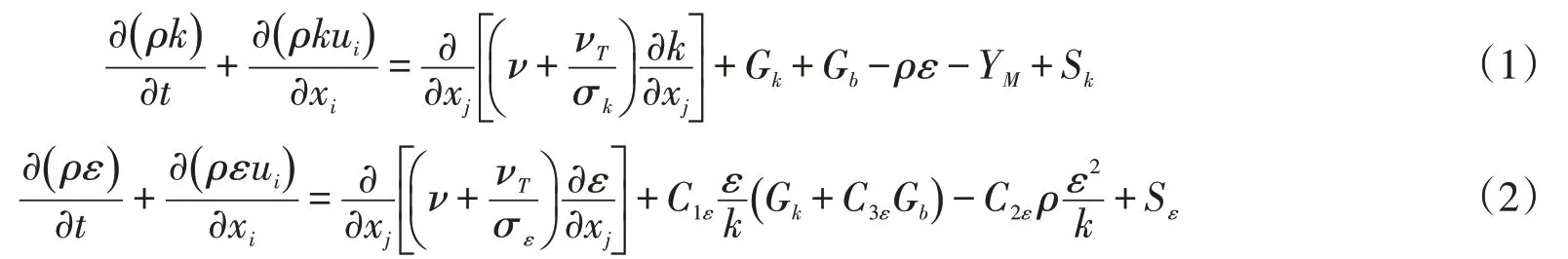
非平衡壁面函数法对黏性底层不进行求解，而是使用半经验公式计算k、ε和切向速度，将其和完全发展的湍流区域联系起来，进而求解出整个流域。

模型计算的边界条件与文献［4］中的相同。

2.2 测点布置

为了得出办公塔楼表面各点在不同方向风荷载作用下的风压，在模拟过程中两塔楼共布置120 个测点，测点的具体布置情况如图6。测点的命名由塔楼号、高度号和点号共同确定，如IA1表示塔楼I，A高度处（即标高为50 m）1 位置处的点。同时，为了后面求解平均风压，对结构的各面进行了命名，分别为F1～F4。

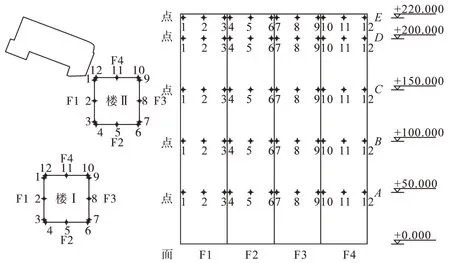
图6 测点布置图Fig.6 Layout of pressure points

2.3 各测点风压

采用上述方法进行模拟计算得出各测点的风压值。在抗风设计中，若考虑当地主导风向，此时必须兼顾各风向角下的最大风压值。由于各风向角下平均风压的最大正、负值起着控制作用，故表1和表2分别给出了塔楼Ⅰ和塔楼Ⅱ在12个风向角下各测点出现的平均风压最大正、负值（风压值单位为kN·m-2）。表1和表2中风压的最大正值为负时，表示该测点在任何风向角下都只出现负风压；风压的最大负值为正时，表示该测点在任何风向角下都只出现正风压，此值为绝对值最小正风压。围护结构设计时，可采用表1和表2中的风压值通过式（4）和式（5）可以得出个测点对应的局部体型系数。

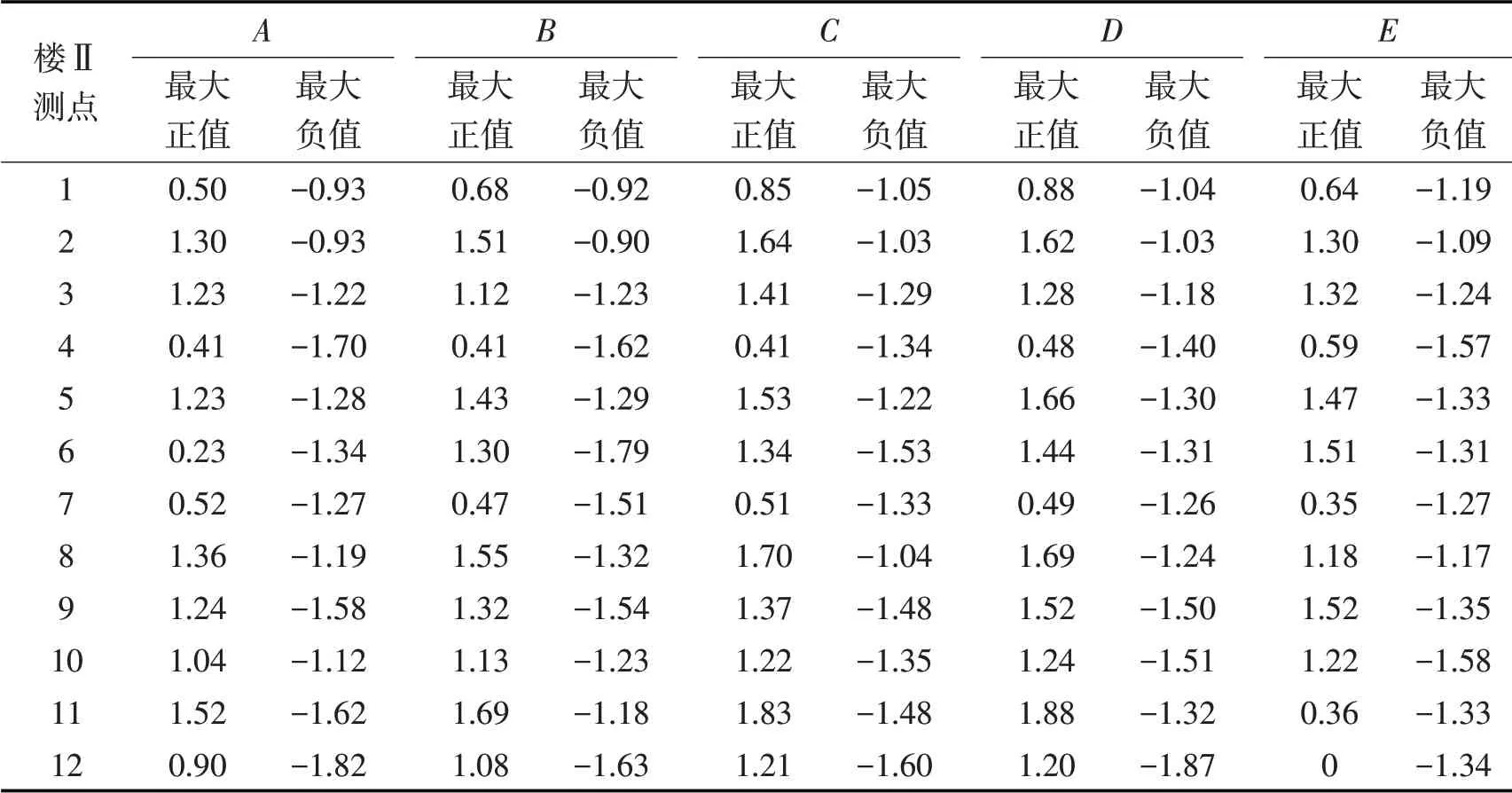
表2 塔楼Ⅱ各测点风压的最大正、负值Tab.2 The maximum positive and negative pressure of Building Ⅱ

2.4 结构体型系数计算

塔楼各立面的平均体型系数可以通过式（3）、式（4）和式（5）的计算得出。

式中：为各面在各个风向角下的平均体型系数；将塔楼结构分为0～50 m，50～100 m，100～150 m，150～200 m，200～220 m这5个区段，An即为各区段的面积；msi为各测点对应的局部体型系数；zr=223.5 m，zi=10 m；Cpi为建筑物表面某测点i的风压系数；Pi是测点i的风压值；r为空气密度，其值为1.25 kg·m-3；Vr是参考点的风速，南昌地区50年一遇的基本风压为0.45 kN·m-2，相当于离地面10 m高度处10分钟的平均最大风速为26.83 m·s-1，故参考点223.5 m处的风速Vr=44.11 m·s-1.

为了解结构各面体型系数的变化，将各测点的高度和模拟计算所得的风压值Pi，结合式（3）、式（4）和式（5）得出各个风向角下的各面平均体型系数，如表3所示。由于结构的分析结果基本对称，故下文结果均只给出0°～150°范围内的6个结果，180°～330°范围内的结果可以参考对应的角度结果得到。

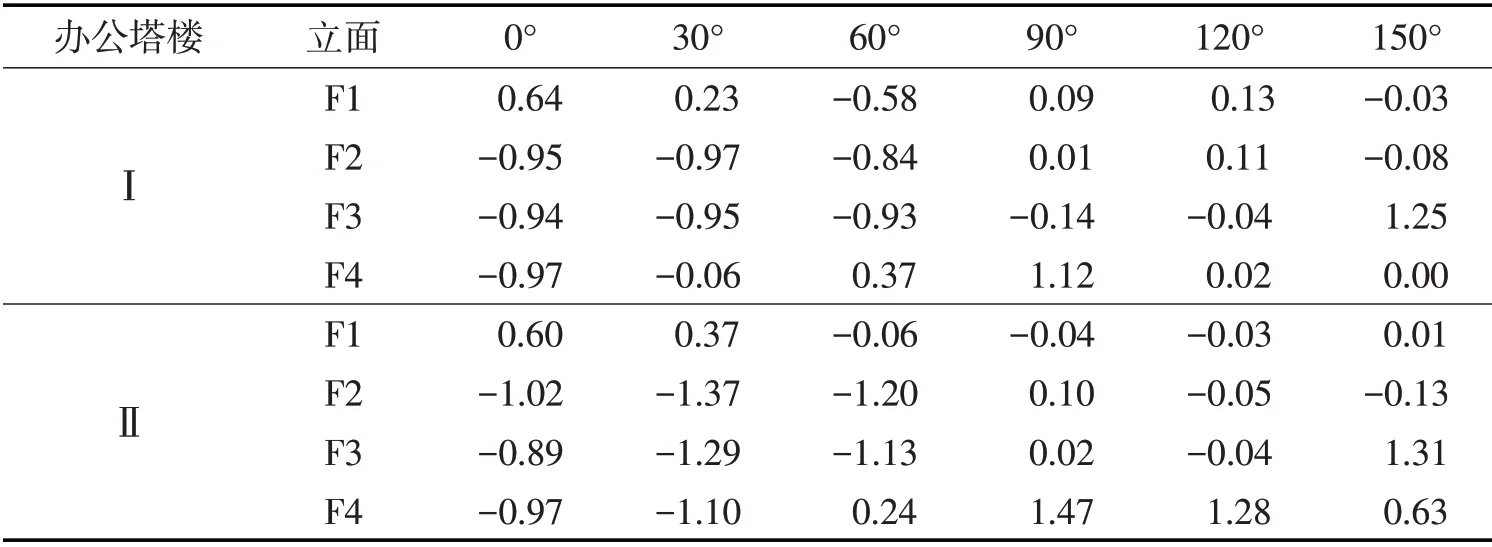
表3 各面平均体型系数Tab.3 The average shape coefficient of each facade

结合以上各面平均体型系数，利用式（6）、式（7）可得塔楼整体体型系数，结构整体体型系数可以用于承重结构设计。

其中μFi为Fi面的体型系数，x轴和y轴由图2确定。由于两办公塔楼具有较大的对称性，所以在塔楼结构设计中结构x和y方向体型系数绝对值的最大值是主要关心的参数。表4中给出了0°～150°范围内结构x和y方向体型系数绝对值的最大值。从表4可以看出，对于x方向，0°和30°较为不利；对于y方向，60°和90°较为不利；塔楼Ⅰ和Ⅱ结构的风荷载体型系数最大绝对值分别为1.58和1.66，为塔楼的抗侧力结构、围护构件的风荷载设计提供了参考依据。由《荷规》可知，本项目中塔楼Ⅰ、Ⅱ作为单体建筑时的风荷载体型系数最大绝对值均为1.4，与表4中最大绝对值对比可知，建筑间距对建筑的风荷载体型系数影响较大。

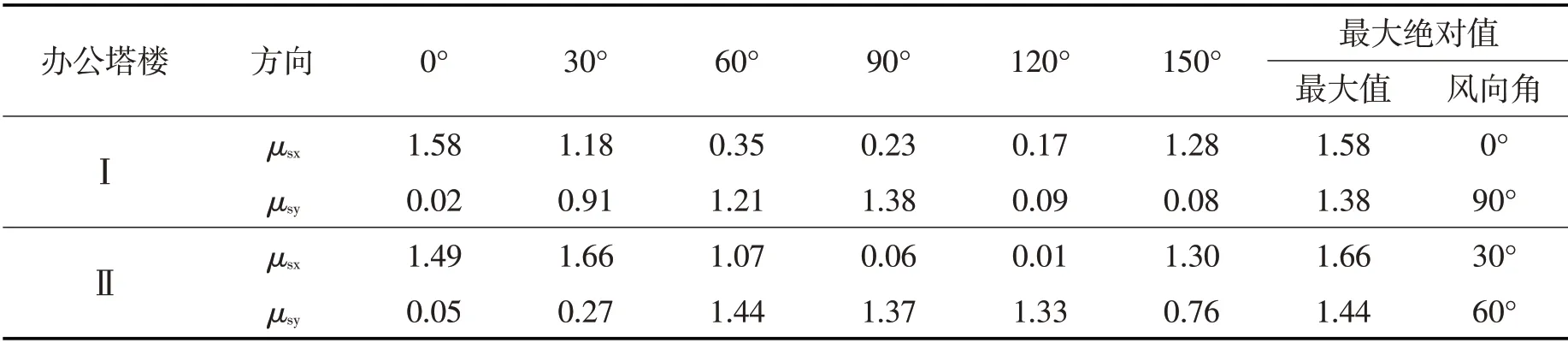
表4 结构x方向和y方向体型系数绝对值Tab.4 Shape coefficient absolute value of the structure X direction and Y direction

3 结论

通过上述分析，可以得出如下结论：

1）模型中采用标准k-ε湍流模型配合非平衡壁面函数法对塔楼Ⅰ和Ⅱ结构风荷载进行计算，可以较为精确的模拟钝体绕流问题；

2）塔楼Ⅰ和Ⅱ结构风荷载体型系数最大绝对值出现在以下风向角：0°和30°（x方向），以及60°和90°（y方向），数值模拟得出的塔楼Ⅰ和Ⅱ结构的风荷载体型系数为塔楼的抗侧力结构、围护构件的风荷载设计提供了参考依据；

3）高层建筑群由于群楼产生的湍流效应对高层建筑结构的风荷载体型系数影响不可忽视，同时还受到建筑物间距的影响。

[1]《建筑结构荷载规范》(GB50009-2012)[S].中国人民共和国国家标准,2012.

[2]杨伟,黄鹏,顾明.高层建筑风致静力干扰效应的试验和数值研究[J].同济大学学报,2004,32(2):152-156.

[3]沈祺,王国砚,顾明.多幢高层建筑物间风场数值模拟和风灾分析[J].同济大学学报:自然科学版,2008,36(5):592-597.

[4]张敏,楼文娟,何鸽俊,等.群体高层建筑风荷载干扰效应的数值研究[J].工程力学,2008,25(1):179-185.

[5]郑朝荣,张文元,张耀春,等.某发电厂景观烟囱的风载体型系数研究[J].工业建筑,2008,38(S):259-263.

[6]曲文超.高层建筑结构风荷载数值模拟研究[D].天津:天津大学,2010.

[7]吴剑锋,王彩华,张文福.湍流模型对建筑物风荷载体型系数数值模拟的影响[J].科学技术与工程,2011,11(6):1368-1370.

[8]赵鹏抟,王国砚.基于数值模拟的某通信塔风荷载体型系数研究[J].结构工程师,2012,28(1):82-86.

[9]黄宏,杨超,张安哥,等.圆钢管混凝土不等偏压柱的有限元计算[J].华东交通大学学报,2009,26(6):11-15.

[10]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.