激发兴趣 学会学习

谢银勇肖智敏

（1.重庆市南川区东胜小学校 重庆南川 408400；2.重庆市南川区水江大桥小学 重庆南川 408400）

激发兴趣 学会学习

谢银勇1肖智敏2

（1.重庆市南川区东胜小学校 重庆南川 408400；2.重庆市南川区水江大桥小学 重庆南川 408400）

本论文探讨了小学数学教学过程中，如何鼓励学生发问，从而激发学生学习数学的浓厚兴趣，诱发其求知欲，积极探索解决问题的方法，逐渐形成能力，学会学习。

发问 兴趣 求知欲 探索 授人以渔

著名的心理学家皮亚杰指出：“一切真理都要由学生自己获得，或由他重新发明，至少由他重建，而不是简单地传递给他。”因此我们在研究小学数学课堂教学方法的同时，还应注重对学生学习的兴趣和教会学生学习方法的研究。下面谈谈我们的初步探索。

一、鼓励发问 满足好奇心

“思维自疑问和惊奇开始。”学习是学生从不知到知的探索过程，学生是在对新知识的一连串问题的思考中学习的，所以要鼓励学生多发问。要使学生能发问，发好问，必须有充分的时间对他们进行训练，可以开展提好问的竞赛，但对于差生提的问题，无论是否有价值，是否有创新，是否有代表性，都应该给予积极鼓励，正确引导，让他们爱上发问，逐渐提高发问的质量。要充分发扬教学民主，启发或引导学生积极思维。一旦学生的思想活跃起来，求知的欲望自然就会增强。

二、激发兴趣 诱发求知欲

兴趣引出动机，动机产生克服困难的意志。如教“乘法分配律”，课本由应用题引入，再揭示规律，我们根据教学实际改成式题引入。复习时安排下面一组题：

当学生计算出结果后，引导他们将相等的两个式子用等号连接起来，再想一想，等号前后两个式子有什么区别与联系。于是学生便从等式（8十35）×5=8×5+35×5中发现了乘法对加法的分配律，并感受到了运用乘法分配律能使计算简便，于是激起学习数学的浓厚兴趣。

有了浓厚的兴趣，学生便会产生对新知识的渴求，想对未知事物进行了解，对问题进行探索，因此学生的求知欲被自然而然诱发。

三、引导探索 培养爱好

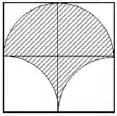
爱好能促使学生将好奇心，求知的要求和学习目的紧紧地联系起来，比兴趣更持久。因此在教学中，要积极引导学生进行探索，让学生从成功的喜悦中感到学习数学的乐趣，从而越来越喜爱数学学习。如教学“下图中正方形的面积是24平方厘米，求阴影部分的面积”时，学生解答为：①先求圆的半径的平方？24÷4=6（厘米2）（即一个小正方形面积恰好等于圆的半径的平方）；②求圆心角是90°的扇形面积：（3.14×6）÷360× 90=4.71（厘米2）；③再求小正方和圆心角是90°的扇形的面积差：6-4.71=1.29（厘米2）；④后求阴影部分面织：（4.71十1.29）×2=12（厘米2）。若能引导学生用割补的方法把阴影部分图形拼成一矩形，学生不难发现还有24÷2=12（厘米2）这种既简便又合理的算法。又如一学生在学习了课本上把圆等分拼成长方形来推导圆面积公式后提出：可以用三角形来推导圆面积公式。他将每个扇形看成一个近似三角形，底为2πr/16（等分成16份），高为r，面积则为：2πr/16×r÷2×16，于是有S=πr2；后来他们又推出了用周长直接算圆面积的公式为S=πd2/4。虽然这些公式在运用中比较麻烦，但学生爱好数学、敢于探究的精神却得到了培养。

四、教给方法 授人以渔

学生掌握科学的学习方法，是知识转化为能力的“中介”，是促进学习能力的形成和发展的必要手段。数学教学中应教给学生哪些方法呢？

1.观察、比较、推理、归纳等是学习数学的基本方法。在小学数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征。学生只有掌握了这一基本方法后，才能更好地学习新知。

2.有效的记忆方法。记忆是人脑对外界所输入的信息进行编码、保持和再现的过程。很多人觉得数学学习只要理解，无需记忆。其实这种观点是错误的。数学学习也离不开记忆，数学中的公式、概念需要记忆，解题模型也需要记忆，只有在记忆的基础上，才能更好地掌握数学知识，灵活地运用数学知识去解决实际问题。同时，记忆也是积累数学经验、丰富数学知识的重要途径。记忆可以使所学的知识在大脑中形成表象，这样才有继续学下去的可能，没有记忆，数学学习就是一句空话。因此，在数学教学中，教师不仅要传授数学知识，而且要教会学生记忆方法。

让学生知道常用数据要牢记，概念、公式要理解记，知其然还要知其所谓然，在记忆过程中还要引导学生通过对比等方法寻求规律巧妙记，同时还可通过编儿歌、顺口溜帮助记。

3.自学课本的方法。学生通过自学课本，自己探索解答相关问题的方法，这是培养学生独立获取知识和发展能力的重要环节。因此，自学课本的方法显得尤为重要。

4.正确的解题方法。在解题中会分析关键字词，通过关键字词解决数学问题，还要学会用多种思路思考，掌握一些常见的解题技巧。

5.有效的检查验算方法。学生要养成检查验算的好习惯，但检查验算也因题而异，也不是一成不变的。如可以通过估算知道其答案范围，也可以把解题结果带回题中验证，还可以用另一路思路解后对比，也可以针对易错处重点检查。

6.及时总结与反思的方法。学生应学会及时总结与反思解题规律，要注意回顾以下问题：1.本题最重要的特点是什么？2.解本题用了哪些基本知识与基本图形？3.本题你是怎样观察、联想、变换来实现转化的？4.解本题用了哪些数学思想、方法？5.解本题最关键的一步在那里？6.是否做过与本题类似的题目吗？在解法、思路上有什么异同？7.本题能发现几种解法？其中哪一种最优？那种解法是特殊技巧？在什么情况下采用吗？把这一连串的问题贯穿于解题各环节中，逐步完善，持之以恒，学生解题的心理稳定性和应变能力就可以不断提高，思维能力就会得到锻炼和发展。