底水油藏水平井控流完井数值模拟耦合模型

陈 阳，彭志刚，王绍先，张建国，张 磊，马明新

（中国石化胜利石油工程有限公司钻井工艺研究院，山东东营257017）

底水油藏水平井控流完井数值模拟耦合模型

陈 阳，彭志刚，王绍先，张建国，张 磊，马明新

（中国石化胜利石油工程有限公司钻井工艺研究院，山东东营257017）

为了预测控流完井条件下底水油藏水平井生产动态并设计关键控流参数，以数值模拟方法为数学求解手段，建立三维空间油水两相混合网格耦合模型，引入“拟传导率”概念，使得耦合模型中包含的油藏渗流、井筒管流和筛管控流3种数学模型可写成统一线性数学表达形式，从而方便建立大型线性方程组求解。结果表明：拟传导率反映相邻网格之间井筒管流或筛管控流流动过程中某相流体流量和压降的比率，流体流动阻力越大，则拟传导率越小，反之亦然；相比常规裸眼井下滤砂管完井，用耦合模型设计控流参数的控流完井方法使得实例井流入流率剖面、油藏渗流压降剖面、水脊前缘上升剖面和见水时间剖面更加均衡，见水时间大幅延长。

底水油藏；水平井；控流完井；数值模拟；耦合模型；混合网格；拟传导率

控流完井已成为实现油藏向水平井均衡供液目的的关键技术，其中控流参数设计工作是决定控流完井控流效果的核心内容。为此，国内外诸多专家学者在详细论述控流机理基础上，建立了描述控流完井条件下底水油藏水平井生产动态数值模拟模型［1-3］。该数值模拟模型包含了油藏渗流、筛管控流和井筒管流3种流动模型的耦合模型［4-6］，其求解手段通常是：使用有限差分黑油模型处理器，如EclipseTM，处理油藏渗流模型；使用有限差分井下网络模型处理器，如NEToolTM、GAPTM、PipesimTM和ReoTM等处理井筒管流模型；根据筛管控流特性开发可编程模块，在有限差分井下网络模型处理器中处理筛管控流模型［7-9］。为了完成整个耦合模型的模拟过程，起初须人工操作实现所有时间步内各处理器之间的数据传输［10-12］，运行效率低下，后来开发出专用耦合工具［13-15］，如ResolveTM、S3connectTM、Field Planning ToolTM和AvocetTM等，运行效率有所提高。由于求解耦合模型须整合多个处理器，其运算精度、运算速度和操作简便性不能令人满意。为解决该问题并丰富数值模拟基础理论研究工作，延伸油藏数值模拟方法中传导率概念，笔者提出拟传导率概念，使得井筒管流模型和筛管控流模型在任一迭代步中可写成与油藏渗流模型相同的“传导率×势差=累积项”的统一数学形式，从而实现耦合模型精确、统一和高效地求解。

1 模型建立

1.1 模型基本流动方程

模型采用混合网格［16］如图1所示，以便准确反映远井区油藏渗流、近井区油藏渗流、井筒管流和筛管控流的流动过程。

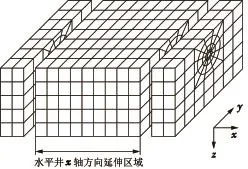
图1 混合网格示意图Fig.1 Hybrid grid sketch

使用三维空间油水两相混合网格黑油模型描述油藏渗流过程［17］，远井区油藏油水两相渗流方程（笛卡尔坐标系）：

近井区油藏油水两相渗流方程（圆柱坐标系）：

式中，下标l=o，w分别表示油相和水相；下标x，y，z表示笛卡尔坐标系中3个轴向；下标r，θ表示圆柱坐标系中径向和周向；下标sc表示标准状态；p为流压，Pa；S为相饱和度；h为相对基准面的垂向高度，m；Δx、Δy、Δz、Δr、Δθ为网格块对应轴向尺寸，m；A为面积，m2；Vb为网格块体积，m3；ρ为密度，kg/m3；g为重力加速度，g=9.81 m/s2；μ为黏度，Pa·s；k为绝对渗透率，m2；kR为相对渗透率；φ为孔隙度；B为体积系数；t为时间，s；q为网格块点汇产量，m3/s。

井筒管流质量守恒方程：

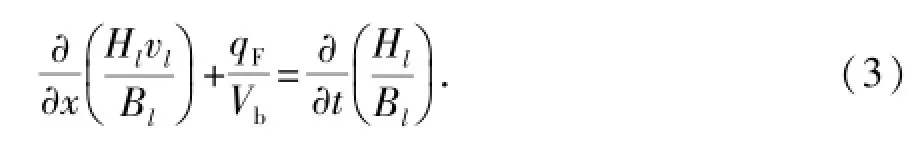
井筒管流动量方程：

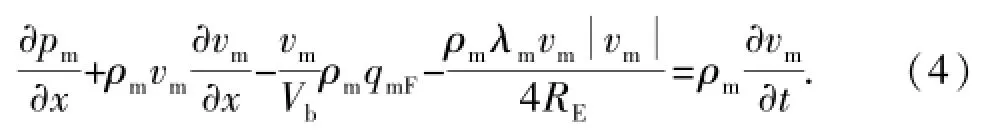
式中，下标m表示油水两相混合流体；下标E表示井筒管流过流通道；R为半径，m；v为井筒管流表观流速，m/s；qF为井壁流入流量，m3/s；ρ为密度，kg/ m3；H为相持率；λ为沿程水力摩阻系数。

控流筛管的控流压降方程［18］（以节流喷嘴型流入控制器为例）：

式中，下标ICD表示流入控制器；D为公称直径，m；η为节流系数。

1.2 模型有限差分近似方程

建立的油水两相混合网格耦合模型拟采用SEQ法进行油藏数值模拟求解；然而大量试算表明，由于混合网格内部不同区域的网格尺寸差异较大、时间步长选择不合理、存在强非线性参数和差分方程本身存在截断误差等原因，计算结果（尤其是后续时间步的计算结果）稳定性并不好。由此提出“简单迭代SEQ法”解决上述问题，即对单个时间步进行简单迭代，迭代控制条件是质量守恒判定原则，要求油相井壁流入流量求解值与水平井原油产量求解值之差足够小。

描述油藏渗流过程的式（1）由偏微分方程写成有限差分近似方程表述如下：

其中

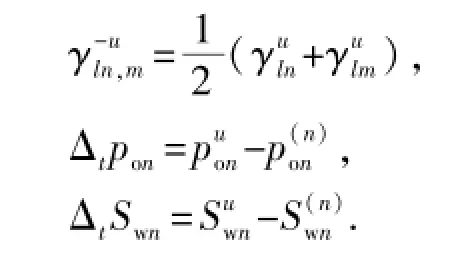
式中，下标n表示当前网格块的自然排序编号；下标m表示相邻网格块的自然排序编号；下标cow表示油水两相毛管作用；上标（n）表示当前时间步序号；上标u表示当前时间步中当前迭代步序号；Z为真垂向深度，m；To、Tw分别为相邻网格块间油相和水相的渗流传导率，m3/（s·Pa）；Cop、Cwp分别为油相和水相的流压系数，m3/（s·Pa）；Cow、Cww分别为油相和水相的饱和度系数，m3/s。

描述井筒管流过程的式（3）、（4）由偏微分方程写成有限差分近似方程表述如下：

质量守恒方程：

动量守恒方程：

其中

式中，下标i为当前井筒网格块的网格块法排序编号；下标a为加速度分量；下标f为摩阻分量；下标T为随时间变化相关分量；Δt为时间步长，s。

在式（8）、（9）中，等号右边第一项表示与时间变化相关的加速压降，第二项表示与空间变化相关的加速压降，第三项表示沿程水力摩阻压降。

耦合模型写成有限差分近似形式后，则可提出耦合条件：即对于混合网格中任一网格块，无论存在源汇点与否，无论与相邻网格块之间质量交换形式是油藏渗流、筛管控流或井筒管流，在所有时间步内，都满足各相流体质量守恒条件。

2 拟传导率

在使用简单迭代SEQ法求解混合网格压力和饱和度时遇到一些困难，原因是井筒管流模型和筛管控流模型具有非线性性质，给耦合模型求解带来极大困难。

为解决上述问题，参照油藏渗流传导率概念，提出井筒管流拟传导率和筛管控流拟传导率概念，如图2所示。“井筒管流拟传导率”的物理含义是单位势差下相邻两个井筒网格块之间某相流体在标准状态下的井筒管流体积通过量。根据定义可写出其表达式：

将更新后的水平井生产段产液剖面代入井筒管流模型，计算得到井筒管流流压剖面，则可使用式（10）更新“井筒管流拟传导率”。

图2 拟传导率示意图Fig.2 Pseudo conductivity sketch

“筛管控流拟传导率”的物理含义是单位势差下流经控流筛管（忽略控流筛管管壁厚度）所在井筒网格块边界的某相流体在标准状态下的节流流动（以节流喷嘴型流入控制器为例，则为节流喷嘴射流）体积通过量。“筛管控流拟传导率”具有如下形式的表达式：

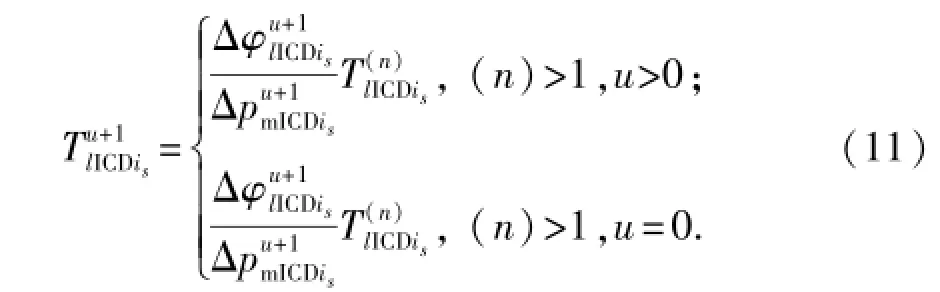
式中，次下标s表示控流筛管编号；ΔφICD为某相流体在控流筛管内外网格块之间的势差，Pa。

式（11）具有递推形式，其中ΔφICD和ΔpmICD都反映了控流筛管内外壁面的势差，不同的是ΔφICD为通过求解混合网格系统的压力得到的值，ΔpmICD为通过求解筛管控流模型得到的值。式（11）在数学层面上反映了在当前时间步内利用筛管控流模型不断修正油水两相混合网格耦合模型中的“筛管控流拟传导率”。式（11）的递推初值将在完成ICD尺寸设计工作时获得。

“拟传导率”概念的引入使得混合网格中任一网格块在任一迭代步中的质量守恒方程都可统一写成“传导率×势差=累积项”的线性数学表达形式，从而使得耦合模型易于列出大型线性方程组求解。隐式求解混合网格压力和饱和度系数矩阵的系数分布示意如图3所示。

图3 隐式求解系数矩阵的系数分布示意图Fig.3 Coefficient matrix structure in implicit solution process

在图3中，系数矩阵被横向分为1、2、3共3个区域，被纵向分为a、b、c共3个区域。其中区域1表示笛卡尔坐标系网格区域网格方程，区域2表示圆柱坐标系网格区域网格方程，区域3表示中心圆柱形网格区域网格方程，区域a、b、c分别表示笛卡尔坐标系、圆柱坐标系和中心圆柱形网格区域网格系数。

3 关键控流参数求解方法

通常情况下控流筛管上控流组件的控流参数在入井前地面装配过程中已固定，生产过程中无法改变，此时控流参数通常根据油井投产初期的地层岩石及流体参数状况确定，即在t（1）时间步中计算得出。控流参数包括完井管柱上控流筛管、盲管、常规筛管和管外封隔器（ECP）的数目和分布情况，由于本文中以节流喷嘴型流入控制器为例，则控流参数还包括控流筛管上节流喷嘴的数目和公称直径。控流组件节流特性对节流喷嘴公称直径敏感，通常将其作为模型求解未知量，即关键控流参数；其他控流参数取预设值，作为模型已知量，即预设控流参数。节流喷嘴公称直径计算流程如图4所示。

使用控流完井方法将水平井生产段井筒壁面流入流率剖面（简称流率剖面）调节成何种状态（称为调剖指标或目标流率剖面）以便达到最佳开发效果，是控流完井方法控流参数设计过程首要考虑的问题。给出的控流完井方法调剖指标制定原则是：通过设计合理的控流参数，在水平井生产段适当部位制造合理的人工压降，克服井筒跟-趾效应和油藏非均质性对水平井生产动态造成的不利影响；避免过度节流，令水平井的跟端、趾端以及处于相对低渗透油藏区域的生产段充分发挥泄流能力。步骤“使用简单迭代SEQ法计算时间步t（1）内常规完井方式下理想井产液剖面”正是执行上述原则的具体手段，即求得初始状态下理想井在理想生产条件下的产液剖面。理想井不存在井筒管流压降，将实例井的井筒管流拟传导率设定为无限大即可，计算过程的其他参数同实例井。

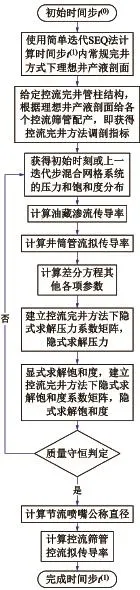
图4 节流喷嘴公称直径计算流程Fig.4 Calculation process of nozzles'nominal diameters

在步骤“计算井筒管流拟传导率”中，对于初始时刻t（0），由于尚未建立起混合网格系统的耦合流动，因此可假设水平井原油配产量沿生产段均匀分布，且无水相产出，据此计算出井筒管流拟传导率。

在步骤“建立控流完井方法下隐式求解压力系数矩阵”和步骤“建立控流完井方法下隐式求解饱和度系数矩阵”中，由于之前已经获得各控流筛管配产量，因此时间步t（1）内穿过边界ΩICDiS（图2）的流量为已知量，即

后续时间步的简单迭代SEQ法流程类似于图4，但不再进行控流完井方法调剖指标和节流喷嘴公称直径两方面的工作，另外“筛管控流拟传导率”改在完成步骤“隐式求解压力”之后执行更新操作。

4 实例计算及其结果分析

4.1 实例参数

实例井及其所在油藏主要已知参数表述如下：底水油藏平均绝对渗透率为0.15 μm2，油藏厚度为14.2 m，原始油藏压力为41.9 MPa，原始油藏岩石孔隙度为25%，岩石压缩系数为1.45×10-4MPa-1。水平井靶点A井深为4300 m，靶点B井深为4 510 m，水平生产段垂深为3 800 m。裸眼井筒直径为0.2159 m，滤砂管外径为0.127 m。标准状态下，原油密度为820 kg/m3，地层水密度为1 030 kg/m3。地层条件下，原油黏度为4 mPa·s，体积系数为1.5，地层水黏度为0.6 mPa·s，体积系数为0.95。其他岩石-流体物性参数如表1、2所示。

表1 毛管压力和相对渗透率Table 1 Capillary pressure and relative permeability data

表2 体积系数和黏度Table 2 Bulk coefficient and viscosity

水平井工作制度：给定初始时刻原油配产量80 m3/d，然后保持对应的井底流压不变，在恒定井底流压条件下生产。

4.2 计算结果及分析

将实例参数代入模型求解，实例井控流参数设计结果如表3所示。

表3 控流参数设计结果Table 3 Flow control parameters design results

完成时间步t（1）后，由模型计算得到的基于表3中控流参数的实例井拟传导率分布剖面如图5所示。

图5 拟传导率分布剖面Fig.5 Pseudo conductivity distribution profile

由图5可知，井筒管流拟传导率反映生产段当前位置井筒管流某相流体流量和压降之间的比率，由于压降近似与流量的平方成正比，因此对于变质量井筒管流，由生产段指端到跟端压降的增幅比流量的增幅越大，对应的井筒管流拟传导率越小。筛管控流拟传导率反映控流筛管对某相流体控流强度的大小，控流强度越大，则控流筛管对流体产生的流动阻力越大，对应的筛管控流拟传导率越小，反之亦然。

由模型计算得到的控流完井和常规裸眼井下滤砂管完井条件下实例井流入流率剖面（开井第35 d）和调剖指标对比如图6所示。

由图6可知，与常规裸眼井下滤砂管完井条件下实例井生产动态相比，使用表3中控流参数的控流完井方法有效抑制了跟-趾效应，使得实例井流入流率剖面更加均衡并接近于调剖指标。

由模型计算得到的控流完井和常规裸眼井下滤砂管完井条件下实例井井筒所在水平面内压力三维等值线分布剖面（开井第35 d）如图7所示。

图6 流入流率剖面对比（开井第35 d）Fig.6 Inflow rate profiles comparison（35 d after well opening）

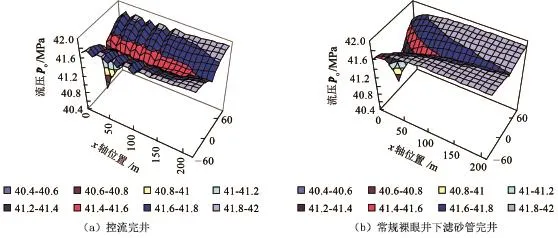
图7 压力三维等值线分布剖面对比（开井第35 d）Fig.7 Comparison of three dimensional isoclines maps of pressure（35 d after well opening）

由图7可知，实例井井筒所在水平面内压力三维等值线分布剖面类似打开的书本状曲面，实例井生产段跟端和趾端分别位于点（0，0）和点（210，0），因此图中压力三维等值线剖面的脊线即为井筒流压剖面。在控流完井条件下，在生产段适当位置引入适当大小的节流压降，使得油藏渗流压降剖面较为均匀，实例井中上游井段的泄流强度得到增强。在常规裸眼井下滤砂管完井条件下，油藏渗流压降（净生产压差）主要消耗在跟端附近，导致生产段泄流强度分布不均。

由模型计算得到的控流完井和常规裸眼井下滤砂管完井条件下实例井水脊前缘三维剖面对比（开井第35 d）如图8所示。

由图8可知，开井第35 d时，控流完井条件下实例井水脊前缘基本呈均衡上升态势且幅度较小，而常规裸眼井下滤砂管完井条件下水脊前缘呈非均衡上升态势并由水平井生产段跟端率先突破。

由范子菲等［19］、Papatzacos等［20］模型和耦合模型计算得到的控流完井和常规裸眼井下滤砂管完井条件下实例井见水时间剖面如图9所示。

范子菲等建立的模型和Papatzacos模型的见水时间剖面由对应完井方法条件下实例井流率剖面分段计算得到。由图9可知，相比常规裸眼井下滤砂管完井，控流完井使得实例井见水时间剖面更加均衡，从而延长了水平井整体见水时间。各模型计算结果略有差异，耦合模型计算结果介于范子菲模型和Papatzacos模型之间。

图8 水脊前缘三维剖面对比（开井第35 d）Fig.8 Comparison of three dimensional water crest front profiles（35 d after well opening）

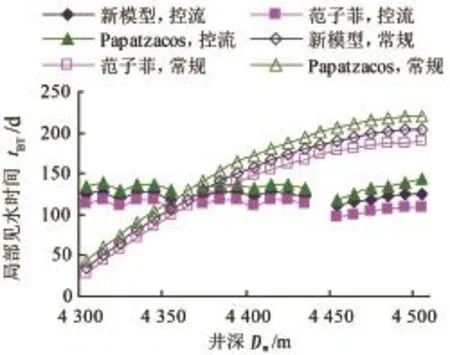
图9 见水时间剖面对比Fig.9 Comparison of water breakthrough time profiles

5 结 论

（1）井筒管流模型和筛管控流模型在任一迭代步中可写成与油藏渗流模型相同的“传导率×势差=累积项”的统一线性数学表达形式，从而方便耦合模型求解。

（2）拟传导率反映相邻网格之间井筒管流或筛管控流流动过程中某相流体流量和压降的比率，流体流动阻力越大，则拟传导率越小，反之亦然。

（3）与常规裸眼井下滤砂管完井相比，由控流完井关键参数设计方法设计出的合理控流参数使得实例井流入流率剖面、油藏渗流压降剖面、水脊前缘上升剖面和见水时间剖面更加均衡，见水时间大幅延长，明显改善了生产动态。

［1］ VALVATNE P H，SERVE J，DURLOFSKY L J，et al. Efficient modeling of nonconventional wells with downhole inflow control devices［J］.Journal of Petroleum Science and Engineering，2003，39（1）：99-116.

［2］ KHELAIWI A L F，DAVIES D.Inflow control devices：application and value quantification of a developing technology［R］.SPE 108700，2007.

［3］ OUYANG L B.Practical consideration of an inflow-control device application for reducing water production［R］. SPE 124154，2009.

［4］ GRUBERT M A，WAN J，GHAI S S，et al.Coupled completion and reservoir simulation technology for well performance optimization［R］.SPE 125251，2009.

［5］ NEYLON K J，REISO E，HOLMES J A，et al.Modeling well inflow control with flow in both annulus and tubing［R］.SPE 118909，2009.

［6］ DAVILA E，DAVILA E，ALMEIDA R，et al.First applications of inflow control devices（ICD）in open hole horizontal wells in Block 15，Ecuador［R］.SPE 123008，2009.

［7］ THORNTON K V，SOLIMAN M Y，JORQUERA R A. Optimization of inflow-control devices or mechanical conformance decisions using a new coupled well-intervention simulator［R］.SPE 139435，2010.

［8］ DANESHY A，GUO B，KRASNOV V，et al.Inflow-control-device design：revisiting objectives and techniques［J］.SPE Production&Operations，2012，27（1）：44-51.

［9］ GURSES S F，AL HASHEMI M，AKHTAR M N，et al. ICD completions optimization for an offshore Abu Dhabi well using dynamic modeling［R］.SPE 165962，2013.

［10］ SHAD S，MAJDI YAZDI M.Wellbore modeling and design of nozzle-based inflow control device（ICD）for SAGD wells［R］.SPE 170145，2014.

［11］ 王金忠，肖国华，陈雷，等.水平井管内分段调流控水技术研究与应用［J］.石油机械，2011，39（1）：60-61. WANG Jinzhong，XIAO Guohua，CHEN Lei，et al.Re-search and application of the staged flow-regulating and water-control technology with screen or tubing in horizontal holes［J］.China Petroleum Machinery，2011，39（1）：60-61.

［12］ 王庆，刘慧卿，张红玲，等.油藏耦合水平井调流控水筛管优选模型［J］.石油学报，2011，32（2）：346-349. WANG Qing，LIU Huiqing，ZHANG Hongling，et al. An optimization model of completion strings with innerlocated nozzle in horizontal wells coupled with reservoirs［J］.Acta Petrolei Sinica，2011，32（2）：346-349.

［13］ 强晓光，姜增所，宋颖智.调流控水筛管在冀东油田水平井的应用研究［J］.石油矿场机械，2011，40（4）：77-79. QIANG Xiaoguang，JIANG Zengsuo，SONG Yingzhi. Research and application of water control screen pipe in Jidong Oilfield horizontal well［J］.Oil Field Equipment，2011，40（4）：77-79.

［14］ 帅春岗，段永刚，冉林，等.水平井ICD控水方法研究［J］.石油钻采工艺，2012，39（1）：60-62. SHUAI Chungang，DUAN Yonggang，RAN Lin，et al. Research on the method of controlling bottom water with inflow control devices（ICD）in horizontal well［J］.Oil Drilling&Production Technology，2012，39（1）：60-62.

［15］ 赵旭，姚志良，刘欢乐.水平井调流控水筛管完井设计方法研究［J］.石油钻采工艺，2013，35（1）：23-27. ZHAO Xu，YAO Zhiliang，LIU Huanle.Technical research on well completion design with inflow control device（ICD）in horizontal wells［J］.Oil Drilling&Production Technology，2013，35（1）：23-27.

［16］ Jr PEDROSA O，AZIZ K.Use of a hybrid grid in reservoir simulation［J］.SPE Reservoir Engineering，1986，1（6）：611-621.

［17］ VICENTE R，VICENTE R，SARICA C，et al.A numerical model coupling reservoir and horizontal well flow dynamics：transient behavior of single-phase liquid and gas flow［R］.SPE 65508，2000.

［18］ 刘成文，李兆敏.锥形喷嘴流量系数及水力参数的理论计算方法［J］.钻采工艺，2000，23（5）：1-3. LIU Chengwen，LI Zhaomin.A theoretical calculation method for flow rate coefficient and hydraulic parameters of conical nozzle［J］.Drilling&Production Technology，2000，23（5）：1-3.

［19］ 范子菲，傅秀娟.气顶底水油藏水平井产能公式和见水时间研究［J］.中国海上油气（地质），1995，9（6）：406-413. FAN Zifei，FU Xiujuan.A study of productivity and breakthrough time of horizontal well in a reservoir with gas-cap and bottom-water drive［J］.China Offshore Oil and Gas（Geology），1995，9（6）：406-413.

［20］ PAPATZACOS P，HERRING T R，MARTINSEN R，et al.Cone breakthrough time for horizontal wells［J］.SPE Reservoir Engineering，1991，6（3）：311-318.

（编辑 沈玉英）

A new numerical coupling model of horizontal well completed with flow control method in bottom water reservoir

CHEN Yang，PENG Zhigang，WANG Shaoxian，ZHANG Jianguo，ZHANG Lei，MA Mingxin
（Drilling Technology Research Institute of Shengli Oilfield Service Corporation，SINOPEC，Dongying 257017，China）

A new 3D hybrid grid model for oil-water two-phase was built，in which numerical simulation was carried out to forecast production performance of a bottom water reservoir with horizontal wells completed using a flow control technique. The new model consists of reservoir flow，wellbore flow and ICD pipe flow control models.A parameter of"pseudo conductivity"was defined in order to linearize the flow in wellbore and ICD pipe and to unify the mathematical expressions of all the three flow models，and then a system of linear equations coupling with the three flow models can be readily established and solved.The pseudo conductivity parameter is calculated as the ratio of the flow rate versus pressure drop for a certain fluid phase passing through adjacent grids by wellbore flow or the controlled flow through ICDs.The simulation results of a case study show that，the larger the flow resistance is，the smaller the pseudo conductivity will be，and vice versa.In comparison with the conventional open hole sand control completion method，the flow control method can greatly delay water breakthrough time by improving the performance of inflow and reducing the pressure drop in near wellbore region.The new model can provide a theoretical guidance for the design and application of the flow control completion method.

bottom water reservoir；horizontal well；flow control completion；numerical simulation；coupling model；hybrid grid；pseudo conductivity

TE 3

A

陈阳，彭志刚，王绍先，等.底水油藏水平井控流完井数值模拟耦合模型［J］.中国石油大学学报（自然科学版），2015，39（6）：110-117.

CHEN Yang，PENG Zhigang，WANG Shaoxian，et al.A new numerical coupling model of horizontal well completed with flow control method in bottom water reservoir［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（6）：110-117.

1673-5005（2015）06-0110-08

10.3969/j.issn.1673-5005.2015.06.015

2015-02-24

国家重大科技项目（2011ZX05022-006）；中国石油化工股份有限公司科技攻关项目（JP12009）

陈阳（1985-），男，博士，研究方向为水平井智能完井理论与技术。E-mail：slchenyang@163.com。