励磁放大倍数对系统电压稳定性的影响研究

张 栩， 刘雪茹

(1.贵州电网公司电网规划研究中心，贵州贵阳550002；2.国网四川省电力公司内江供电公司，四川内江641000)

分岔理论是非线性科学的一个重要分支，是对非线性动态系统进行结构稳定性机理分析的有力工具。电力系统是典型的非线性动态系统，在其电压稳定性问题的研究中，应当考虑动态元件的作用[1]，此时应用分岔理论来研究电力系统电压稳定性问题具有重要的意义。

影响电力系统电压稳定性的因素很多，励磁系统与负荷则是公认的两个最主要因素。本文主要基于分岔理论，研究对负荷节点电压影响较大的励磁放大倍数对系统电压稳定性的影响。分析在负荷、励磁放大倍数两个控制变量作用下的系统电压稳定性，并从分岔控制的角度，提出参数优化策略。

1 系统模型

1.1 励磁控制系统模型

在自并励静态励磁系统中，励磁放大倍数受发电机机端电压的影响，能更好反映出其对系统电压的影响。所以本文采用静态励磁系统模型作为本文的励磁系统模型，如图1。

将偏差量引入模型框图，化简得到励磁系统微分方程：

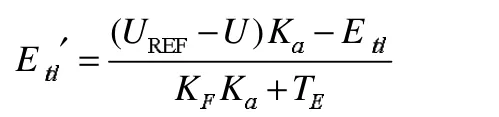
式中：U为负荷节点电压。

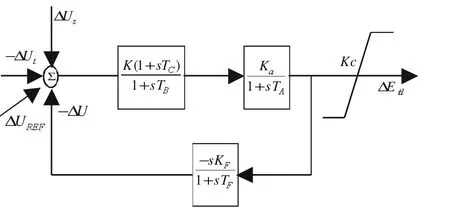
图1 静态励磁系统模型框图

1.2 发电机模型

发电机模型选用三阶模型，不计阻尼绕组的影响，具体模型为[1]：

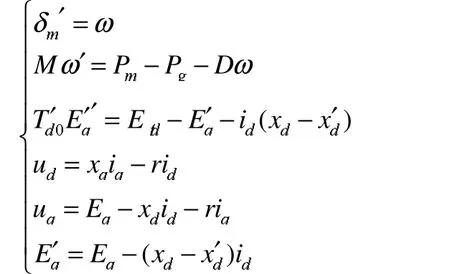
1.3 负荷模型

负荷模型选择WALVE负荷模型，具体模型为[2]：

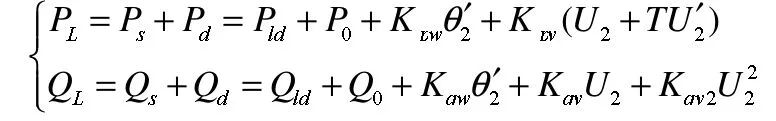
1.4 网络方程

采用两机5节点小干扰分析模型，网络连接如图2所示。系统微分方程为：

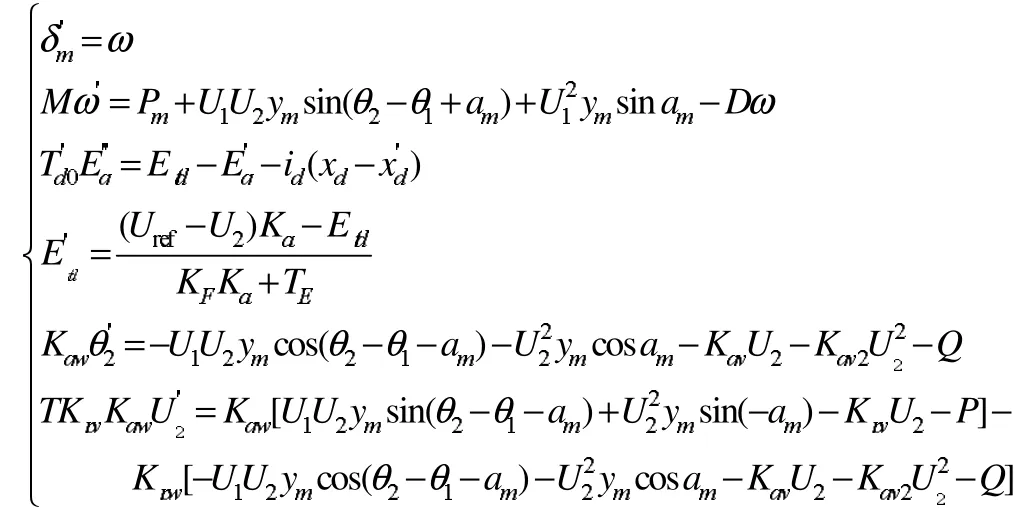
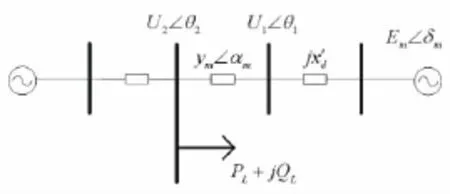
图2 两机小干扰分析模型

状态变量初始值为：

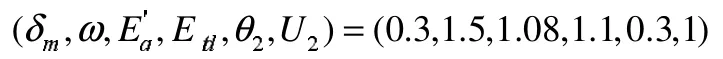
控制参数初始值为：

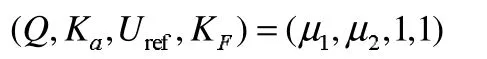
2 分岔分析

基于分岔分析软件Matcont得到随着负荷参数的改变，Ka变化对于系统分岔点的影响。分岔理论认为系统在出现极值分岔(LP)后将面临电压失稳，所以对于第一个LP点之后的研究显得意义不大。主要关注的是分岔点的个数，第一个Hopf分岔点位置和第一个LP分岔点位置。

由于Matcont在双(多)参数分岔分析中的限制，不能导出整个双(多)参数分岔的平衡解流形，只能通过手动更改，得到一个近乎为曲面的平衡解流形图截面。本文选择Ka为7、9、11、13、15、20、30时的分岔图进行分析，详见图3。为更直观看到各分岔点变化情况，将图转换为二维平面图，详见图4。

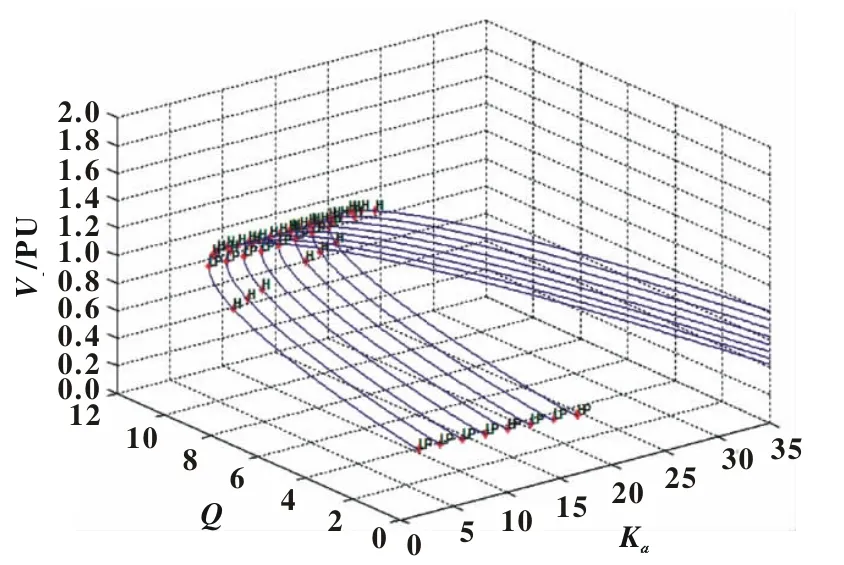
图3 Q、Ka双参数分岔3D图

由图4可知，随着Ka的增大，系统分岔点数目会减少，但Ka不是越大越好，过大的Ka会增加系统Hopf分岔，容易造成系统电压振荡，不利于系统电压稳定性。

随着Ka的增大，第一个Hopf分岔点均朝着左下方移动，电压不断减小，且不断靠近系统初始电压(系统初始电压值为1)。分岔理论认为，分岔点电压越接近系统运行电压，即表明此时系统电压稳定裕度越低，系统更易面临分岔，从而导致电压失稳。由图4可知，Ka越大，第一个Hopf分岔点就越容易出现，且对应的无功裕度也在不断下降，不利于系统电压稳定性。

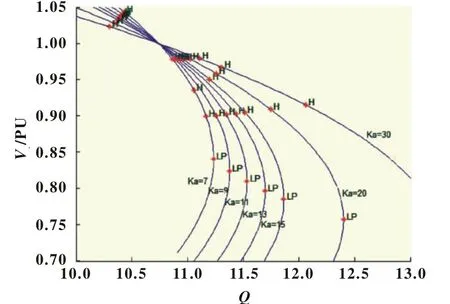
图4 Q、Ka双参数分岔平面图

随着Ka的增大，第一个LP分岔点均朝着右下方移动，电压不断远离系统初始电压，电压裕度不断增加，说明系统不易电压崩溃，而对应的无功裕度也在不断增加，说明Ka越大，越有利于系统极值分岔点位置，越有利于系统电压稳定性。

采取第一个Hopf分岔点和第一个LP分岔点的电压、无功值，整理后得表1。由表1可知，Ka越大，第一个Hopf分岔点越容易出现，而极值分岔点不易出现，说明随着Ka的增大，不利于Hopf分岔点的位置，但却有利于极值分岔点位置。文献[2]认为Hopf分岔点对应系统电压震荡，极值分岔对应系统电压极限。由此可知增大励磁放大倍数一方面能够提高系统稳定极限，另一方面却容易造成系统电压震荡，说明采用高放大倍数的励磁调节器在提高励磁效率的同时，还需要通过调节器的限制和保护来实现其稳定运行[3-5]。

表1 Q、K双参数分岔分析表

3 时域仿真

进一步用时域仿真来验证上述分析的正确性。基于PSASP搭建3机9节点系统模型，仿真励磁放大倍数Ka对系统电压的影响。选取Ka值为10、100、115、120时的系统电压时域仿真图，如图5。

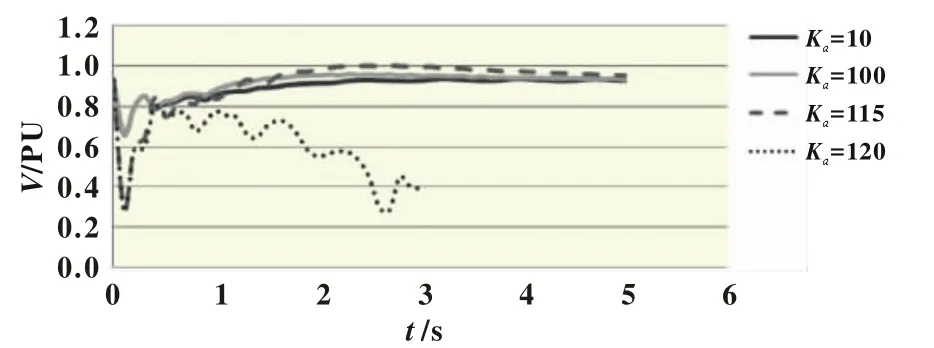
图5 不同Ka值时的机端电压时域仿真图

由图5可知，对于故障后的电压恢复，Ka不是越大越好，最好的Ka值为80，可恢复电压到0.95；当Ka＞115时，系统电压将不能恢复；当Ka＜10时，系统不收敛；以恢复时间来看，Ka越大，恢复时间越短；较短的恢复时间有利于系统电压稳定性；以恢复效果来看，Ka越小，恢复系统电压的能力越弱，对于系统电压的控制效果也越差，若Ka过大，系统会发生振荡失步，最后导致系统电压崩溃。不同Ka值的故障恢复电压与电压稳定时间详见表2。

由表2知，励磁增益Ka不是越大越好，Ka越大，电压稳定时间越短，动态性能指标越好，但过大的Ka会增加系统负阻尼带来的系统振荡，导致故障恢复后的系统电压偏低[6-7]。

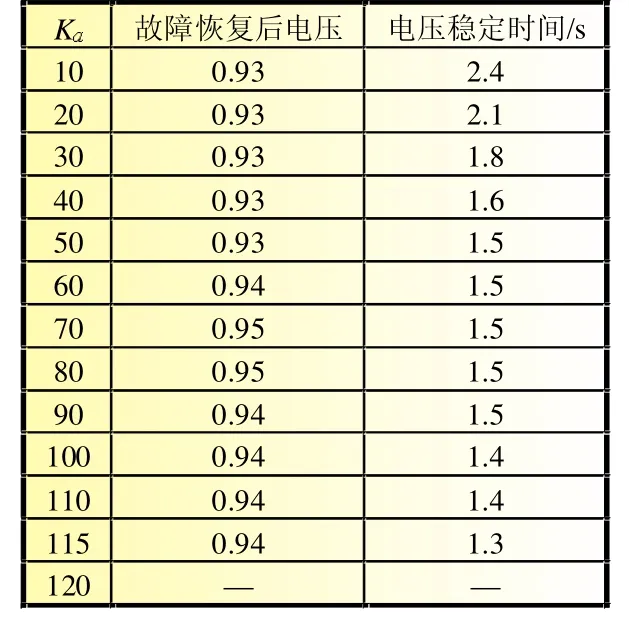
表2 励磁增益K对电压的影响

4 总结

基于分岔理论的电力系统电压稳定性分析表明，励磁放大倍数Ka的增大虽延迟了系统极值分岔，提高了系统电压极限，但却增加了系统Hopf分岔，使得系统容易发生电压震荡。而电力系统电压失稳若以极值分岔的出现作为评判标准过于乐观，极值分岔之前往往发生Hopf分岔，所以基于分岔理论的电压稳定性分析认为励磁放大倍数Ka不是越大越好。基于PSASP的时域仿真也验证了这点，Ka取值过大会带来系统振荡，不利于系统电压恢复。高放大倍数的励磁系统虽提高了励磁效率与发电机调节范围，但从系统层面来看，也加大了系统振荡的风险。高放大倍数的励磁系统应增设相应的限制控制器来保证系统的电压稳定。

[1] 刘取.电力系统稳定性及发电机励磁控制[M].北京：中国电力出版社，2007.

[2] 彭志炜，胡国根，韩祯祥.基于分叉理论的电力系统电压稳定性分析[M].北京：中国电力出版社，2005.

[3] 方思立，苏为民.励磁系统动态性能指标有关标准的分析[J].电力设备，2004，5(7)：7.

[4] 邓集祥，张新宇，童建东.系统参数对Hopf分歧影响的研究[J].电工技术学报，2007，22(9)：9.

[5] 李康，康积涛.基于分岔理论的电力系统动态电压稳定性分析[D].成都：西南交通大学，2012.

[6] 张旭昶，徐政.同步发电机励磁装置及其在PSASP中模型的研究[D].浙江：浙江大学，2006.

[7] 何开教，方鸽飞，刘荣.发电机励磁系统调节参数对电力系统动态电压稳定的影响[J].机电工程，2012，29(1)：1.