STOCHASTIC STABILITY OF UNCERTAIN RECURRENT NEURAL NETWORKS WITH MARKOVIAN JUMPING PARAMETERS∗

M.SYED ALI

Department of Mathematics，Thiruvalluvar University，Vellore，Tamilnadu，India

STOCHASTIC STABILITY OF UNCERTAIN RECURRENT NEURAL NETWORKS WITH MARKOVIAN JUMPING PARAMETERS∗

M.SYED ALI

Department of Mathematics，Thiruvalluvar University，Vellore，Tamilnadu，India

E-mail：syedgru@gmail.com

In this paper，global robust stability of uncertain stochastic recurrent neural networks with Markovian jumping parameters is considered.A novel Linear matrix inequality（LMI）based stability criterion is obtained to guarantee the asymptotic stability of uncertain stochastic recurrent neural networks with Markovian jumping parameters.

Lyapunov functional；linear matrix inequality；Markovian jumping parameters；recurrent neural networks

Key words34K20；34K50；92B20；94D05

1 Introduction

A recurrent neural network，which naturally involves dynamic elements in the form of feedback connections used as internal memories.Recurrent networks are needed for problems where there exist at least one system state variable which cannot be observed.Most of the existing recurrent neural networks were obtained by adding trainable temporal elements to feed forward neural networks（like multilayer perceptron networks［8］and radial basis function networks［4］）to make the output history to be sensitive.Like feed forward neural networks，these network functions as block boxes and the meaning of each weight in these nodes are not known.They play an important role in applications such as classification of patterns，associate memories and optimization（see［1，2，4，8，13，16，19，21，22］and the references therein）.Thus，research on properties of stability problem and relaxed stability problem for recurrent neural networks，became a very active area in the past few years［5，11，17，25-28，38］.

When the neural network incorporates abrupt changes in its structure，the Markovian jump linear system is very appropriate to describe its dynamics.The problem of stochasticrobust stability for uncertain delayed neural networks with Markovian jumping parameters was investigated via LMI technique in［18，32，39，40］.

When one models real nervous systems，stochastic disturbance and parameter uncertainties are unavoidable to be considered.Because in real nervous system，synaptic transmission is a noisy process brought on by random fluctuation from the release of neurotransmitters，and the connection weights of the neuron depend on certain resistance and capacitance values that include uncertainties.Therefore，it is of practical importance to study the stochastic effects on the stability of delayed neural networks with parameter uncertainties，some results related to this problem have been published in［6，10，23，24，36，37］.

In addition，parameter uncertainties can be often encountered in real systems as well as neural networks，due to the modelling inaccuracies and/or changes in the environment of the model.In the past few years，to solve the problem brought by parameter uncertainty，robustness analysis for different uncertain systems has received considerable attention，see for example，［20，29，30，35］.

Inspired by the aforementioned works，we study a class of uncertain Markovian jumping recurrent neural networks with time-varying delays.Further the robust stability analysis for uncertain Markovian jumping stochastic recurrent neural networks with time-varying delays（MJSRNNs）is made.By using the Lyapunov functional technique，global robust stability conditions for the uncertain MJSRNNs are given in terms of LMIs，which can be easily calculated by MATLAB LMI toolbox［7］.The main advantage of the LMI based approaches is that the LMI stability conditions can be solved numerically by using the effective interior-point algorithms［3］.Numerical examples are provided to demonstrate the effectiveness and applicability of the proposed stability results.

2 System Description and Preliminaries

Consider the following stochastic uncertain Markovian jumping recurrent neural networks with time-varying delays described by，

where

and

In which xi（t）is the activation of the ithneuron.Positive constant ai（ηt）denotes the rates with which the cell i reset their potential to the resting state when isolated from the other cells and inputs.wij（ηt）and bij（ηt）are the connection weights at the time t，symbol∆denotes the uncertain term，C（ηt）and H（ηt），are known constant matrices of appropriate dimensions.∆C（ηt）and∆H（ηt）are known matrices that represent the time-varying parameter uncertainties.Fj（·）is the neuron activation function of j-th neuron.τj（t）is the bounded time varying delay in the state and satisfy 0≤τj（t）≤¯τ，0≤˙τj（t）≤d＜1，j=1，2，···，n.

Further，ω（t）=［ω1（t），ω2（t），···，ωm（t）］T∈Rmis a m-dimensional Brownian motion defined on a complete probability space（Ω，F，P），｛ηt，t≥0｝is a homogeneous，finite-state Markovian process with right continuous trajectories and taking values in finite set S=｛1，2，···，s｝with given a probability space（Ω，F，P）and the initial model η0.Let Π=［πij］，i，j∈S，which denotes the transition rate matrix with transition probability

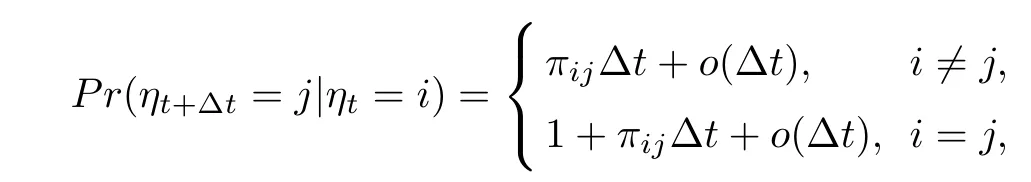
The following assumption is made on the activation function.

（A）The neuron activation functions fj（·）are bounded and satisfies the following Lipschitz condition

for all x，y∈R，j=1，2，···，n，where ljare positive numbers.

Then we have

where L=diag｛l1，l2，···，ln｝.

Remark 2.1 The existence of solutions for the stochasctic functional differential equations with Markovian jumping is explained in Section 4 of［33］and［15］.Therefore，for any initial data ξ∈L2F（［-ρ，0］；Rn）system（2.1）has unique solution（or equilibrium point）denoted by x（t；ξ）or x（t）.

For convenience，each possible value of ηtis denoted by i，i∈S in the sequel.Then we have

where∆Ai，∆Wi∆Bi，∆Ciand∆Hifor i∈S are represent the time-varying parameter uncertainties and are assumed to be of the form:

where Mi，N1i，E2i，N3i，N4iand N5iare known real constant matrices and Fi（t）for all i∈S，are known time-varying matrix functions satisfying

It is assumed that all elements Fi（t）are Lebesque measurable，∆Ai，∆Wi∆Bi，∆Ciand∆Hiare said to be admissible if both（2.2）and（2.3）hold.

System（2.1）can be written as

where

The following lemmas are essential for the proof of main results.

Lemma 2.2（Schur complement［3］）Let M，P，Q be given matrices such that Q＞0，then

Lemma 2.3（see［9］）For any constant matrix M ∈Rn×n，M=MT＞0，scalar η＞0，vector function Γ:［0，η］→ Rnsuch that the integrations are well defined，the following inequality holds

Lemma 2.4（see［9］） For given matrices D，E and F with FTF≤I and scalar ǫ＞0，the following inequality holds

3 Robust Stability Results

In this section，some sufficient conditions of asymptotic stability for system（2.1）are obtained.

Theorem 3.1 Suppose that assumption（A）holds，then system（2.1）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0，positive diagonal matrices T1＞0，T2＞0 and positive scalars ǫ1，ǫ2such that feasible solution exist for the following LMIs，

Proof We use the following Lyapunov functional to derive the stability result

where

By Itˆo's formula，the stochastic derivative of V（t，x（t））along the trajectories of system（2.1）can be obtained as

By Jensen's inequality［9］

From assumption（A）we know that

Then，for T1=diag｛t11，···，t1n｝≥0，T2=diag｛t21，···，t2n｝≥0 we have

Finally，from（3.2）-（3.6），we have

where

Then Ξican be written as

By using Lemma 2.4 we have

By using Schur complement lemma Ξican be written as Ωi.

Thus，we have

It is obvious that for Ωi＜0，there must exist a scalar γ＞0 such that，

Taking the mathematical expectation on the both sides of（3.7），one can deduce that

which indicates from the Lyapunov stability theory that the dynamics of the neural network（2.1）is globally，robustly，asymptotically stable in the mean square，which completes the proof.□

In what follows，we will show that our result can be specialized to several cases including those studied extensively in the literature.All corollaries given as follows are consequences of Theorem 3.1 and hence the proofs are omitted.

Case 1 If there are no parameter uncertainties then system（2.1）is simplified to

Corollary 3.2 Suppose that assumption（A）holds，then system（3.8）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0 positive diagonal matrices T1＞0，T2＞0 such that feasible solution exist for，

Proof The proof is similar to that in the proof of Theorem 3.1 by choosing∆Ai=∆Bi=∆Ci=∆Hi=∆Wi=0.Hence it is omitted.

Case 2 If there are no parameter uncertainties and stachastic disturbance then system（2.1）is simplified to

Corollary 3.3 Suppose that assumption（A）holds，then system（3.9）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0 and positive diagonal matrices T1＞0，T2＞0 such that feasible solution exist for，

Proof The proof is similar to that in the proof of Theorem 3.1 by choosing∆Ai=∆Bi=∆Ci=∆Hi=∆Wi=0，Ci=Hi=0.Hence it is omitted. □

Case 3 If there are no parameter uncertainties，stachastic disturbance and Markovian jumping parameters then system（2.1）is simplified to

Corollary 3.4 Suppose that assumption（A）holds，then system（3.10）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0 and positive diagonal matrices T1＞0，T2＞0 such that feasible solution exist for，

Proof The proof is similar to that in the proof of Theorem 3.1 by choosing s=1，πij=0，∆Ai=∆Bi=∆Ci=∆Hi=∆Wi=0，Ci=Hi=0.Hence it is omitted. □

Case 4 We now present the stability condition of the following stochastic Hopfield neural networks with time varying delays，

Corollary 3.5 Suppose that assumption（A）holds，then system （3.12）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0，positive diagonal matrices T1＞0，T2＞0 and positive scalars ǫ1，ǫ2such that feasible solution exist for the following LMI，

Proof The proof is similar to that in the proof of Theorem 3.1 by choosing Bi（t）=Ci= Hi=0.Hence it is omitted.

Case 5 We now present the stability condition of the following stochastic Hopfield neural networks with time varying delays and without Markovian jumping parameters，

Corollary 3.6 Suppose that assumption（A）holds，then system（3.13）is said to be asymptotically stable，if there exist symmetric positive definite matrices P＞0，Q＞0，R＞0，S＞0，positive diagonal matrices T1＞0，T2＞0 and positive scalars ǫ1，ǫ2such that feasible solution exist for the following LMI，

Proof The proof is similar to that in the proof of Theorem 3.1 by choosing s=1，πij=0， Bi（t）=Ci=Hi=0.Hence it is omitted.

Remark 3.7 Theorem 3.1，Corollaries 3.2-3.6 are depends on the size of time delay element，which means that it is less conservative than those delay-independent ones，especially when the delay value is very small，and this may create a gap of LMI-based delay-dependent results for stochastic delayed neural networks.It is realized that，the problems studied in many other papers such as［5］，［30］，［31］and［34］are also a special class of this paper.

4 Numerical Examples

Example 1 Consider the stochastic recurrent neural network（2.2）with uncertainties and Markovian jumping parameters is of the following form:

with the following parameters，

By using the Matlab LMI toolbox［7］，we solve the LMI（4）for ǫi＞0（i=1，2），¯τ=1.9 and d=0.5 the feasible solutions are

Therefore，the concerned neural networks with time-varying delays is asymptotically stable.

Example 2 Consider the neural network with variable delay［34］with

By solving the LMI（14）for s=1，¯τ=10.5 and d=0.5 the feasible solutions are

Therefore，the concerned neural networks with time-varying delays is asymptotically stable. It was reported in［34］，the maximal admissible time delay for the delay-dependent stability condition in［34］is¯τ=0.29165.However，by Corollary 3.4 and using LMI toolbox，for d=0.5 it is found that the maximal admissible time delay for the stability of the system described by Example 2 is¯τ＞0.Thus our result makes less conservative result than that in［34］.

Example 3 Consider the stochastic Hopfield neural network with variable delay［31］with

L=0.5I3，N1=0.6I3，N2=0，N3=N4=N5=0.2I3，M=diag｛0.1，0.5，0.3｝.

By solving the LMI（17）for s=1，¯τ=4.9 and d=0.5 the feasible solutions are

Therefore，the concerned neural networks with time-varying delays is asymptotically stable.It was reported in［31］，the maximal admissible time delay for delay-dependent stability condition in［31］is¯τ=0.6.However，by Corollary 3.6 and using LMI toolbox，for d=0.5 it is found that the maximal admissible time delay for the stability of the system described by Example 3 is¯τ=4.9.Thus our result makes less conservative result than that in［31］.

5 Conclusion

A new sufficient condition is derived to guarantee the asymptotic stability of the equilibrium point for uncertain stochastic Markovian jumping recurrent neural networks with time-varying delays.A linear matrix inequality approach has been developed to solve the problem in this paper.We obtained some novel delay-dependent sufficient conditions for the stability and constructed the linear matrix inequalities.The effects of both variable ranges of time delay and parameter uncertainties are taken into account in the proposed approach.Illustrative numerical examples have been provided to demonstrate the effectiveness of the proposed method.Our results can be specialized to several cases including those studied extensively in the literature.

We think it would be interesting to investigate the possibility of extending the results to more complex neural network systems with time-varying and distributed delays，such as uncertain network systems，stochastic BAM neural network systems and Cohen-Grossberg neural network system.These issues will be the topic of our future research.

［1］Arik S.On the global asymptotic stability of delayed cellular neural networks.IEEE Trans Circ Syst I，2000，47:571-574

［2］Balasubramaniam P，Lakshmanan S，Rakkiyappan R.Delay-interval dependent robust stability criteria for stochastic neural networks with linear fractional uncertainties.Neurocomputing，2009，72:3675-3682

［3］Boyd B，Ghoui L，Feron E，Balakrishnan V.Linear Matrix Inequalities in System and Control Theory. Philadephia，PA:SIAM，1994

［4］Billings S A，Fung C F.Recurrent radial basis function networks for adaptive noise cancellation.Neural Networks，1995，8:273-290

［5］Cao J，Wang J.Global exponential stability and periodicity of recurrent neural networks with time delays. IEEE Trans Circ Syst I，2005，52:920-931

［6］Chen W H，Lu X M.Mean square exponential stability of uncertain stochastic delayed neural networks. Phys Lett A，2008，372（7）:1061-1069

［7］Gahinet P，Nemirovski A，Laub A，Chilali M.LMI Control Toolbox User's Guide.Massachusetts:The Mathworks，1995

［8］Giles C L，Kuhn G M，Williams R J.Dynamic recurrent neural networks:theory and applications.IEEE Trans Neural Netw，1994，5:153-156

［9］Gu K.An integral inequality in the stability problem of time-delay systems//Proceedings of 39th IEEE CDC.Sydney:Philadelphia，1994

［10］Huang H，Feng G.Delay-dependent stability for uncertain stochastic neural networks with time-varying delay.Physica A，2007，381（15）:93-103

［11］Hu S，Wang J.Global asymptotic stability and global exponential stability of continuous time recurrent neural networks.IEEE Trans Automat Cont，2002，47:802-807

［12］Khasminski R.Stochastic stability of Differential Equations.Netherlands:Sijithoff and Noordhoff，1980

［13］Kwon O M，Lee S M，Park Ju H，Cha E J.New approaches on stability criteria for neural networks with interval time-varying delays.Appl Math Comput，2012，218:9953-9964

［14］Lou X，Cui B.Delay-dependent stochastic stability of delayed Hopfield neural networks with Markovian jump parameters.J Math Anal Appl，2007，328:316-326

［15］Lou X，Cui B.LMI approach for Stochastic stability of Markovian jumping Hopfield neural networks with Wiener process.IEEE Proceedings of the sixth international conference on Intelligent Systems Design and Applications，2006:1-7

［16］Li X.Global robust stability for stochastic interval neural networks with continuously distributed delays of neutral type.Applied Mathematics and Computation，2010，215:4370-4384

［17］Liang J，Cao J.Boundedness and stability for recurrent neural networks with variable coefficients and time-varying delays.Phys Lett A，2003，318:53-64

［18］Liu Y，Wang Z，Liu X.An LMI approach to stability analysis of stochastic high-order Markovian jumping neural networks with mixed time delays.Nonlinear Anal Hybrid Systems，2008，2:110-120

［19］Mahmoud M S，Xia Y.Improved exponential stability analysis for delayed recurrent neural networks.J Franklin Inst，2011，348:201-211

［20］Mao X，Koroleva N，Rodkina A.Robust stability of uncertain stochastic delay differential equations.Systems Control Lett，1998，35:325336

［21］Orman Z，New sufficient conditions for global stability of neutral-type neural networks with time delays. Neurocomputing，2012，97:141-148

［22］Park J H，Kwon O M.Delay-dependent stability criterion for bidirectional associative memory neural networks with interval time-varying delays.Modern Physics Lett B，2009，23（1）:35-46

［23］Syed Ali M，Balasubramaniam P.Global exponential stability for uncertain stochastic fuzzy BAM neural networks with time-varying delays.Chaos Solitons Fractals，2009，42:2191-2199

［24］Syed Ali M，Balasubramaniam P.Exponential stability of uncertain stochastic fuzzy BAM neural networks with time-varying delays.Neurocomputing，2009，72:1347-1354

［25］Syed Ali M.Robust stability of stochastic uncertain recurrent neural networks with Markovian jumping parameters and time-varying delays.Int J Mach Learn Cyber，2014，5:13-22

［26］Syed Ali M.Stability analysis of Markovian Jumping stochastic Cohen-Grossberg neural networks with discrete and distributed time varying delays.Chineese Physics B，2014，23（6）:060702

［27］Syed Ali M.Novel delay dependent stability analysis of Takagi-Sugeno fuzzy uncertain neuralnetworks with time varying delays.Chinese Physics B，2012，21（7）:070207

［28］Syed Ali M.Global asymptotic stability of stochastic fuzzy recurrent neural networks with mixed timevarying delays.Chinese Physics B，2011，20（8）:0802011

［29］Wang Z，Qiao H.Robust filtering for bilinear uncertain stochastic discrete-time systems.IEEE Trans Signal Process，2002，50:560-567

［30］Wang Z，Lauria S，Fang J，Liu X.Exponential stability of uncertain stochastic neural networks with mixed time delays.Chaos Solitons Fractals，2007，32:62-72

［31］Wang Z，Shu H，Fang J，Liu X.Robust stability for stochastic Hopfield neurarl networks with time delays. Nonlinear Anal Real World Appl，2006，7:1119-1128

［32］Xie L.Stochastic robust analysis for Markovian jumping neural networks with time delays.ICNC，2005，1: 386-389

［33］Xu D，Li B，Long S，Teng L.Moment estimate and existence for solutions of stochastic functional differential equations.Nonlinear Analysis，2014，108:128-143

［34］Yang H，Chu T，Zhang C.Exponential stability of neural networks with variable delays via LMI approach. Chaos Solitons Fractals，2006，30:133139

［35］Yu W，Yao L.Global robust stability of neural networks with time varying delays.J Comput Appl Math，2007，206:679-687

［36］Zhang J H，Shi P，Qiu J Q.Novel robust stability criteria for uncertain stochastic Hopfield neural networks with time-varying delays.Nonlinear Anal Real World Appl，2007，8（4）:1349-1357

［37］Zhang H G，Wang Y C.Stability analysis of Markovian jumping stochastic Cohen-Grossberg neural networks with mixed time delays.IEEE Trans.Neural Networks，2008，19（2）:366-370

［38］Zhang H.Robust exponential stability of recurrent neural networks with multiple time varying delays. IEEE Trans Circ Syst II，Exp Briefs，2007，54:730-734

［39］Zhu Q X，Cao J D.Stability analysis of Markovian jump stochastic BAM neural networks with impulse control and mixed time delays.IEEE Trans Neural Networks Learn Syst，2012，23（3）:467-479

［40］Zhu Q X，Cao J D.Exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays.IEEE Trans Syst Man Cybern B，2011，41（2）:341-353

∗Received December 16，2013；revised September 8，2014.The work was supported by NBHM project grant No.2/48（10）/2011-RD-II/865.

The results are derived by using the Lyapunov functional technique，Lipchitz condition and S-procuture.Finally，numerical examples are given to demonstrate the correctness of the theoretical results.Our results are also compared with results discussed in［31］and［34］to show the effectiveness and conservativeness.