A MATHEMATICAL MODEL OF ENTERPRISE COMPETITIVE ABILITY AND PERFORMANCE THROUGH EMDEN-FOWLER EQUATION FOR SOME ENTERPRISES∗
Yueloong CHANG(张裕隆)
Department of Psychology,National Chengchi University,Taipei 116,China
Mengrong LI(李明融)
Department of Mathematical Sciences,National Chengchi University,Taipei 116,China
A MATHEMATICAL MODEL OF ENTERPRISE COMPETITIVE ABILITY AND PERFORMANCE THROUGH EMDEN-FOWLER EQUATION FOR SOME ENTERPRISES∗
Yueloong CHANG(张裕隆)
Department of Psychology,National Chengchi University,Taipei 116,China
E-mail:cyl.88054@gmail.com
Mengrong LI(李明融)
Department of Mathematical Sciences,National Chengchi University,Taipei 116,China
E-mail:liwei@math.nccu.edu.tw;hierteli@gmail.com
In this paper,we work with the ordinary differential equation n2u(n)′′=u(n)pand obtain some interesting phenomena concerning,boundedness,blow-up,blow-up rate,life-span of solutions to those equations.
estimate;life-span;blow-up;blow-up rate;performance;competitive ability
2010 MR Subject Classification 34C
1 Introduction
How to improve the performance and competitiveness of the company is the critical issue of Industrial and Organizational Psychology in Taiwan.We try to design an appropriate mathematical model of the competitiveness and the performance of the 293 benchmark enterprises out of 655 companies.Unexpectedly,we discover the correlation of performance and competitiveness is extremely high.Some benchmark enterprises present the following phenomena:
Competitive ability(force,F(P(n)))is a power function of the performance(P(n));that is,there exist positive performances p>0 and a constant k so that
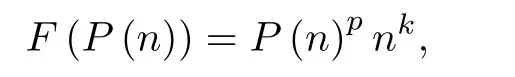
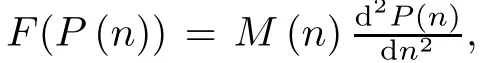
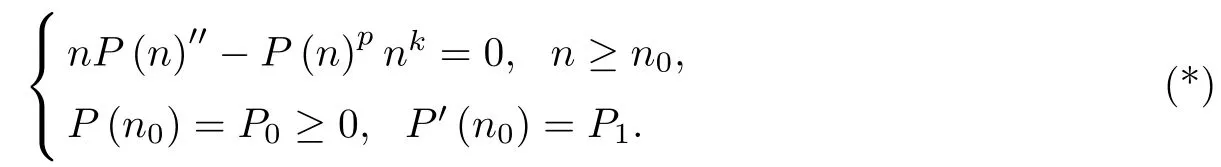
It is clear that the function P(n)pnkis locally Lipschitz function in P,hence by the standard theory,the local existence of classical solutions is applicable to equation(∗).
We would use our methods used in[1-19]to discuss problem(∗)for k=-1;that is,
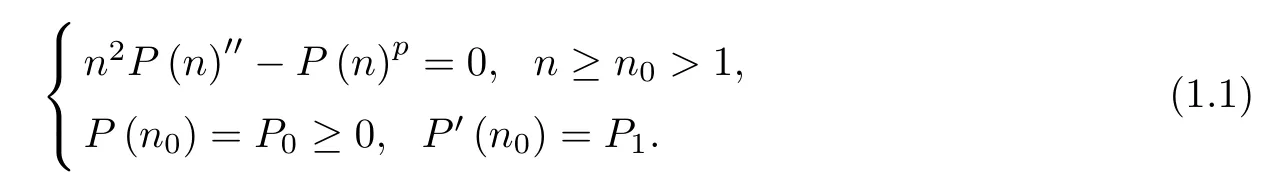
In papers[Li 1-4,6-8],the semi-linear wave equation□u+f(u)=0 under some conditions,some interesting results on blow-up,blow-up rate and estimates for the life-span of solutions were obtained.We want to study the case of Emden-Fowler type wave equation in 0-dimension form,i.e.,to consider the equation n2P(n)nn-△P(n)=P(n)pwith zero-space dimension. For p>1,these functions n-2P(n)pare locally Lipschitz,the local existence and uniqueness of solutions of equation(1.1)for p>1,can be obtained through the standard arguments. Consider the transformation n=es,P(n)=u(s),then n2P′′(n)=-us(s)+uss(s),u(s)p= -us(s)+uss(s)and u(0)=P(1)=P0;us(0)=P′(1)=P1.Therefore,equation(1.1)can be transformed into the form
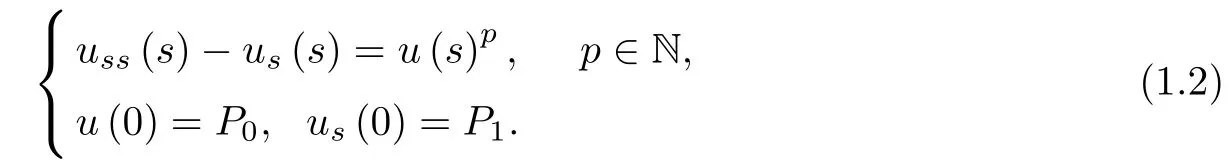
Thus,the local existence of solution u for(1.2)in(0,S)is equivalent to the local existence of solution P for(1.1)in(1,lnS).In this paper,we have estimated the life-span S∗of positive solution u of(1.2)under three different cases.The main results are as follows:
(a)P1=0,P0>0:
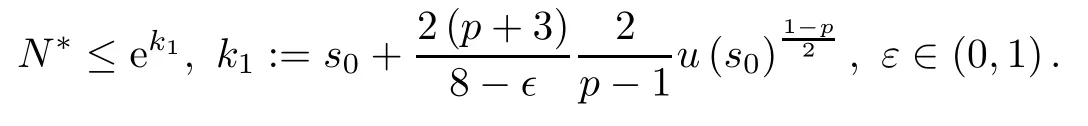
(b)P1>0,P0>0:
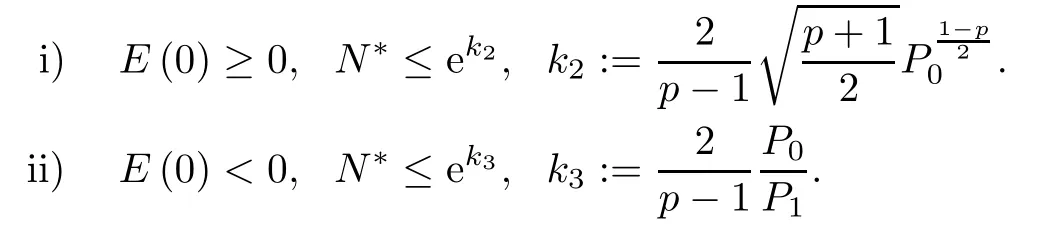
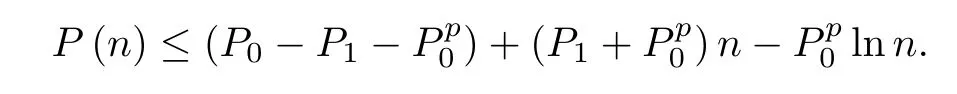
2 Notation and Fundamental Lemmas
For a given function u in this work we use the following abbreviations
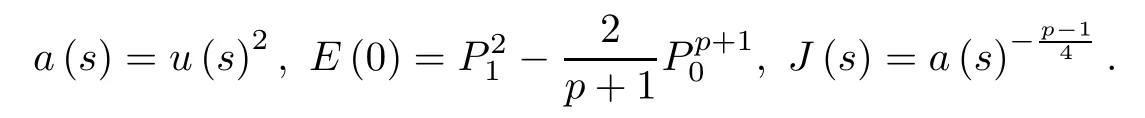
By some calculation we can obtain the following Lemma 1 and Lemma 2,we omit these argumentations on the proof of Lemma 1.
Lemma 1 Suppose that u∈C2([0,S])is the solution of(1.2),then
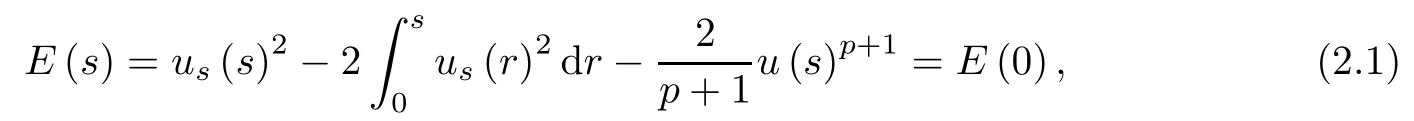
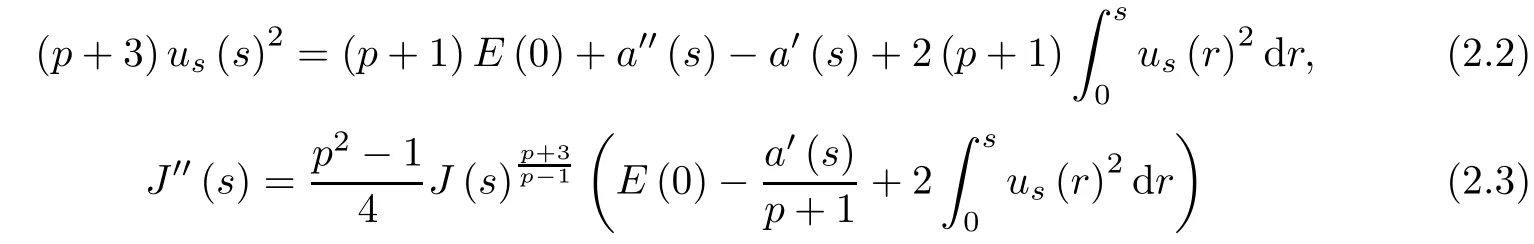
and
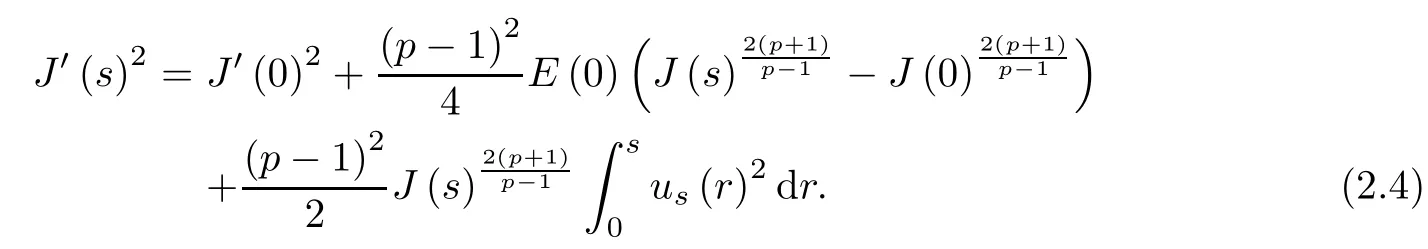
Lemma 2 For P0>0,the positive solution u of equation(1.2),we have
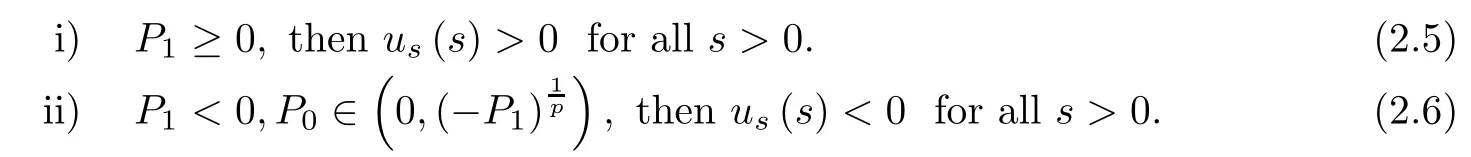
Proof i)uss(0)=P1+Pp0>0,we know that uss(s)>0 in[0,s1)and us(s)is increasing in[0,s1)for some s1>0.Moreover,since u and usare increasing in[0,s1),
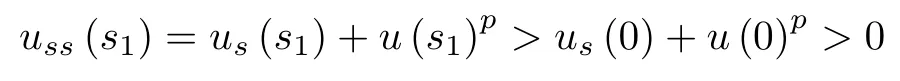
for all s∈[0,s1)andfor all s∈[0,s1),we know that there exists a positive number s2>0,such that us(s)>0 for all s∈[0,s1+s2).
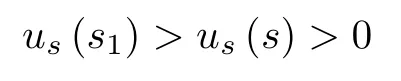
Continuing such process,we obtain us(s)>0 for all s>0.
ii)According to uss(0)=us(0)+u(0)p=P1+Pp0<0,there exists a positive number s1>0 such that uss(s)<0 in[0,s1),us(s)is decreasing in[0,s1);therefore,for all s∈[0,s1)and u(s)is decreasing in[0,s1).
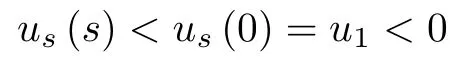
Moreover,since u and usare decreasing in[0,s1),for all s∈[0,s1)and us(s1)<us(s)<0 for all s∈[0,s1),we know that there exists a positive number s2>0,such that us(s)<0 for all s∈[0,s1+s2).
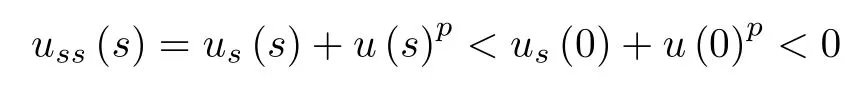
Continuing such process,we obtain us(s)<0 for all s>0.
3 Estimates for the Life-Span of Positive Solution u of(1.2)under
In this section we want to estimate the life-span of positive solution u of(1.2)under P1=0,P0>0.Here the life-span S∗of u means that u is the solution of equation(∗)and u exists only in[0,S∗)so that problem(1.2)possesses the positive solution u∈C2[0,S∗)for S<S∗.
Theorem 3 For P1=0,P0>0,the positive solution u of(1.2)blows up in finite time;that is,there exists a bound number S∗so that
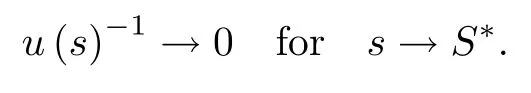
Remark The phenomena of blow-up of u(s)at s=S∗(or P(n)at n=eS∗)means that such benchmark enterprises attain their maximum of performance and competitiveness.
Proof By(2.5),we know that us(s)>0,a′(s)>0 for all s>0 under P1=0,P0>0.
By Lemma 1,
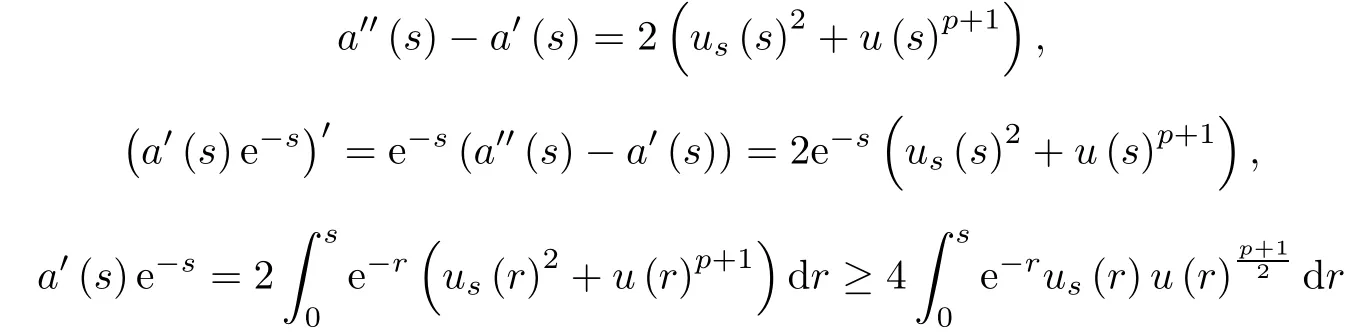
and a′(0)=0,we have
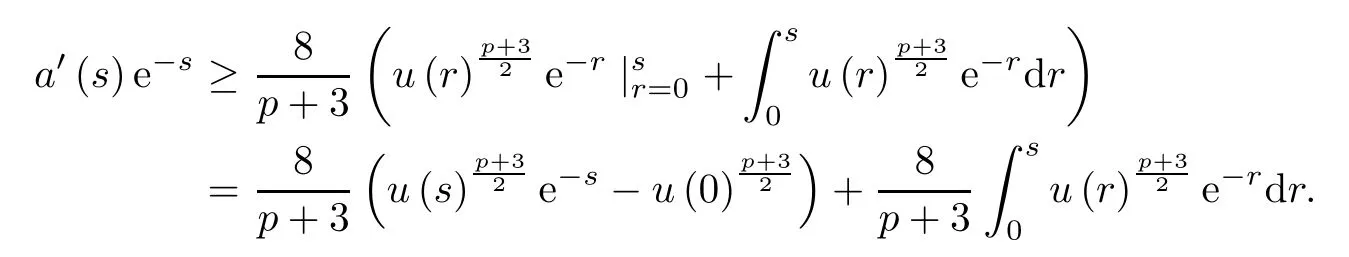
Since a′(s)>0 for all s>0,u is increasing in(0,∞)and
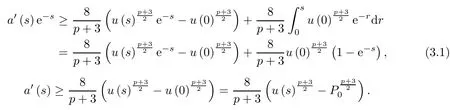
Using P1=0 and integrating(1.2),we obtain
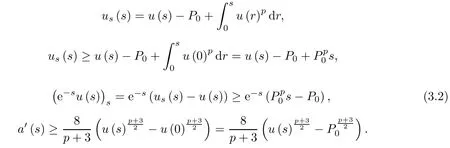
According to(3.2)and u′(s)>0,
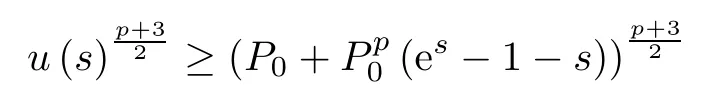
and for all ǫ∈(0,1),we get that
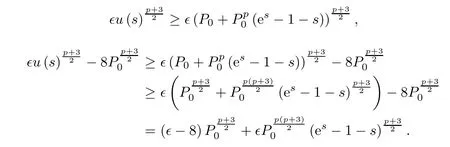
Now,we want to find a number s0>0 such that
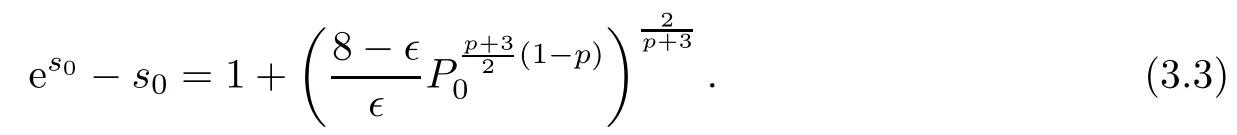
This means that there exists a number s0>0 satisfying(3.3)with ǫ∈(0,1)such that
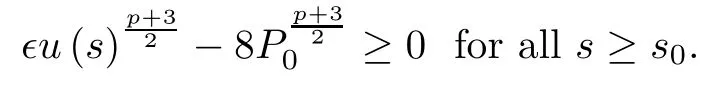
From(3.1),it follows that
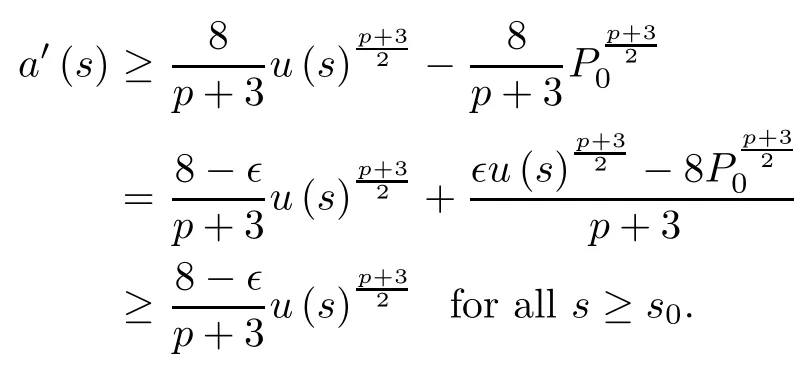
For all s≥s0,ǫ∈(0,1),we obtain that
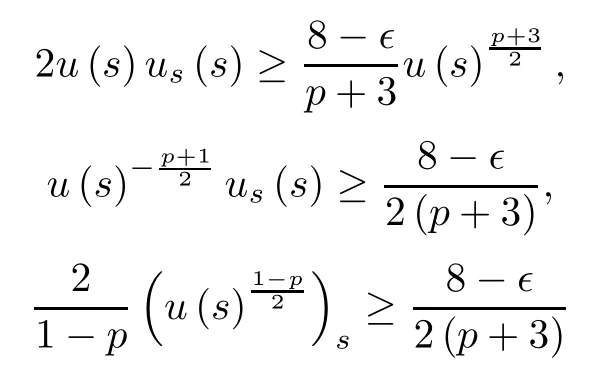
and
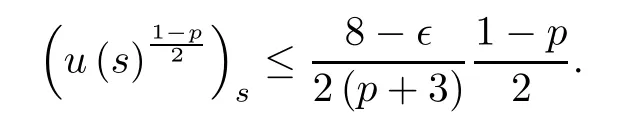
Integrating the above inequality,we conclude that
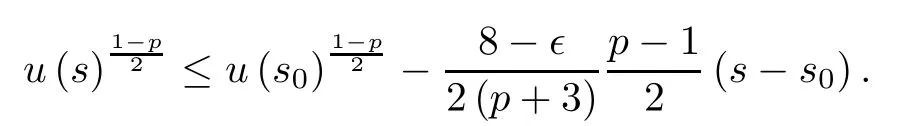
Thus,there exists a finite number
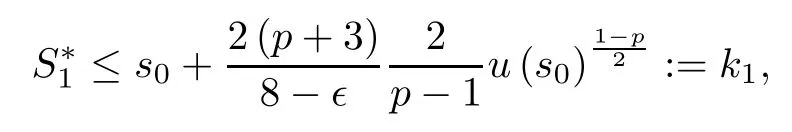
such that u(s)-1→0 for s→S∗1,that is,
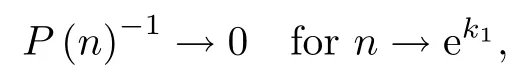
which implies that the life-span N∗of positive solution P is finite and N∗≤ek1.
4 Estimates for the Life-Span of Positive Solution u of(1.2)under
In this section we start to estimate the life-span of positive solution u of(1.2)under P1>0,P0>0.
Theorem 4 For P1>0,P0>0,the positive solution u of(1.2)blows up in finite time;that is,there exists a bound number S∗so that
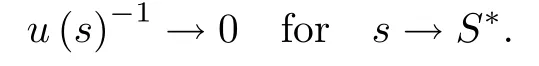
Moreover,for E(0)≥0,we have
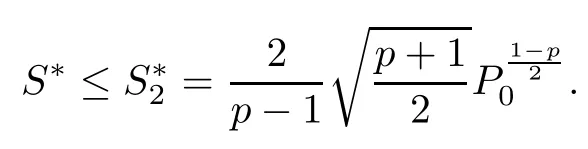
For E(0)<0,we also have
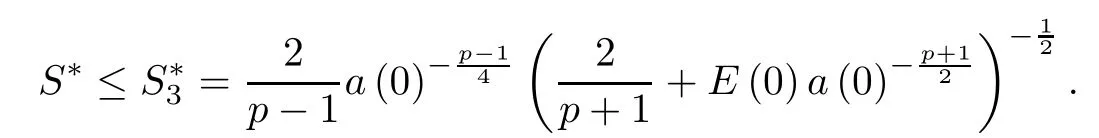
Proof We separate the proof into two parts,E(0)≥0 and E(0)<0.
i)E(0)≥0.By(2.1)and(2.5)we have
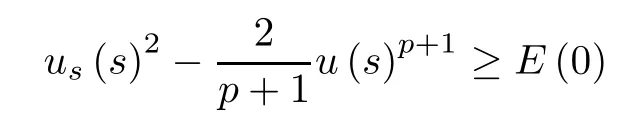
and
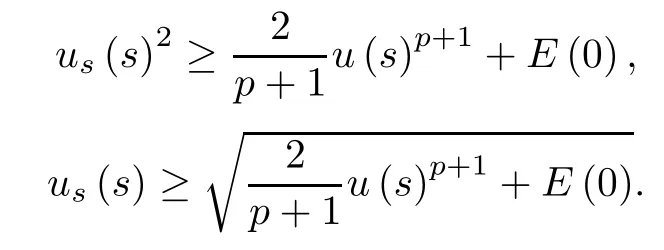
Under the condition E(0)≥0,we get

and
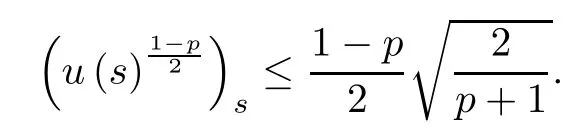
Integrating the above inequality,we obtain

Thus,there exists a finite time

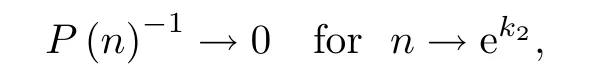
which means that the life-span N∗of positive solution P is finite and N∗≤ek2.
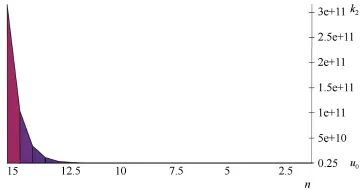
Picture 1 graph of k2,u0∈[0.02,1]
Picture 2 graph of k2,u0∈[1,5]
ii)E(0)<0.From(2.1)and(2.5)we obtain thatus(s)>0 for all s>0 and
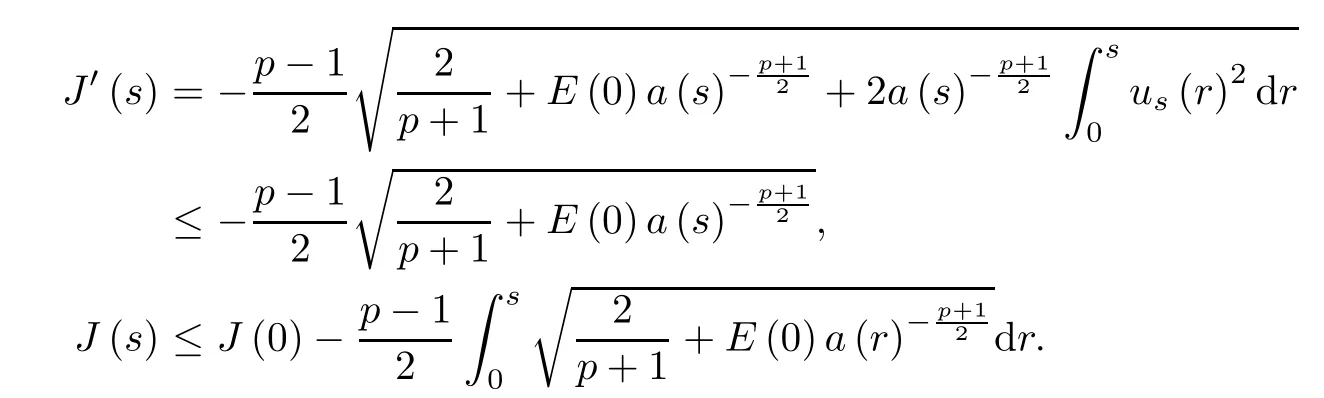
Since E(0)<0 and a′(s)>0 for all s>0,then
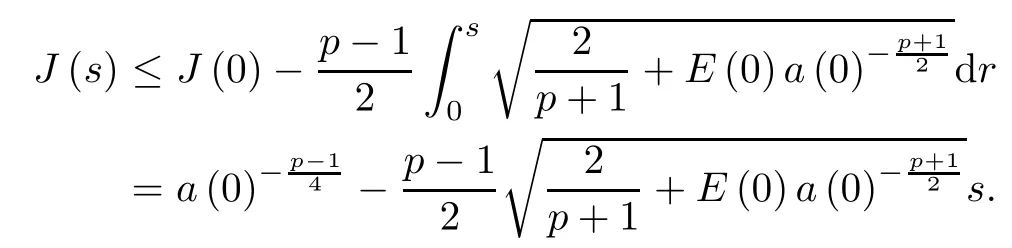
Thus,there exists a finite number
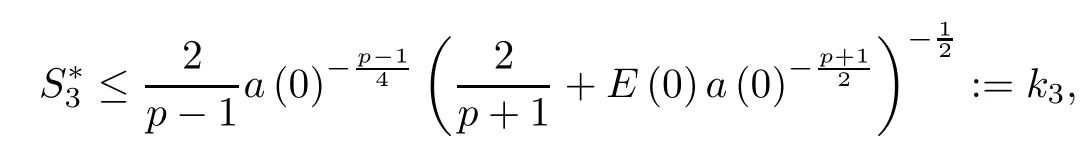
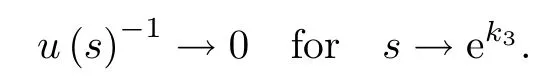
This means that the life-span S∗of u is finite and S∗≤ek3.
5 Estimates for the Life-Span of Positive Solution u of(1.2)under P1<0
Finally,we estimate the life-span of positive solution u of(1.2)under P1<0 in this section.
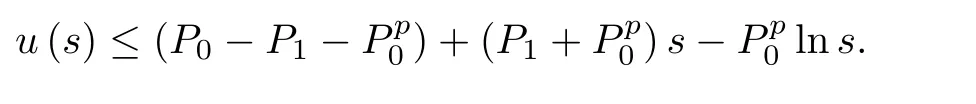
And particularly,for E(0)≥0,then

Remark This boundedness of u or P means that such enterprises will go to their minimum of performance and competitiveness if they enlarge their amount of the surveying rod enterprise's composition department number or the main unit commanders counts;if such number can not be well controlled,they will only go into bankruptcy one day.
Proof i)According to(1.2)and integrating this equation with respect to s,we get
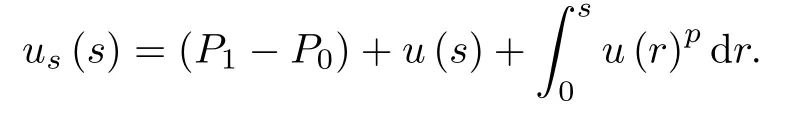
By(2.6),we have u is decreasing and
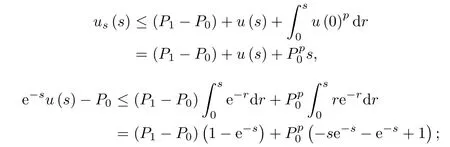
that is,
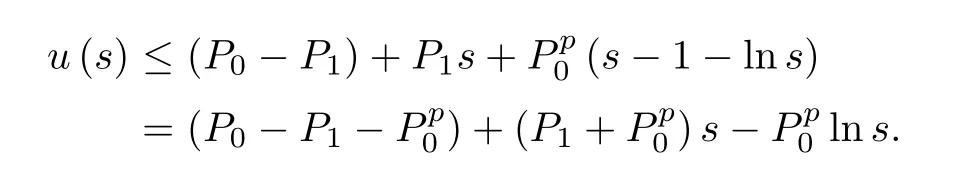
ii)E(0)≥0.By(2.1),we have
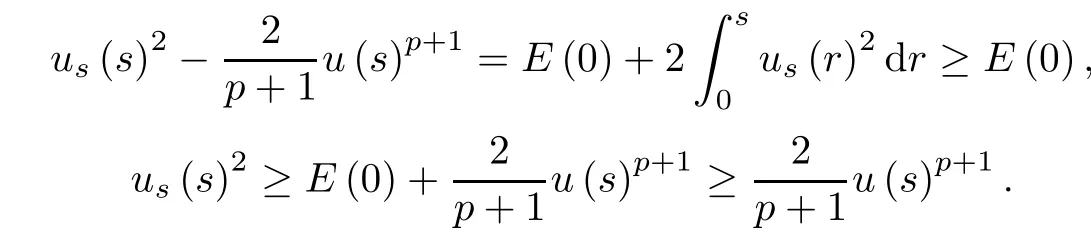
By(2.6),we obtain that
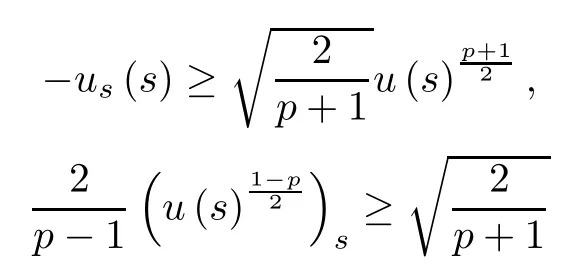
and
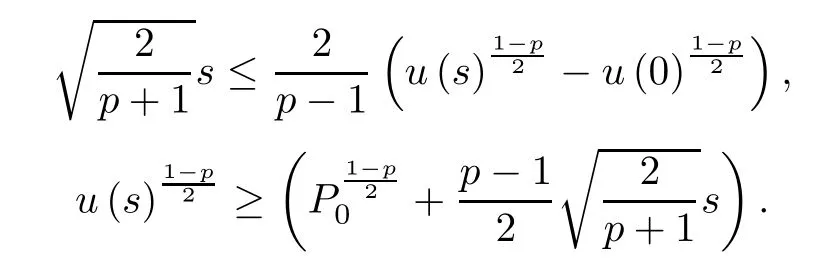
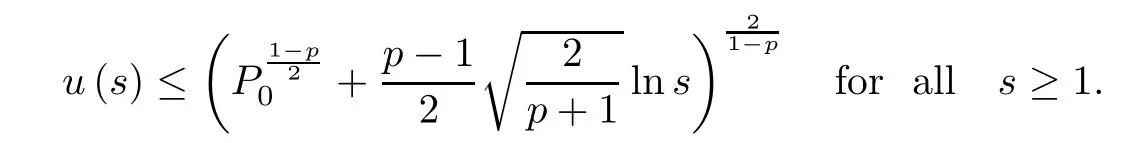
Acknowledgements Thanks are due to Professor Ton Yang for his comments,to Grand Hall and Auria Solar for their financial assistance.
[1]Li M R.Nichlineare Wellengleichungen 2.Ordnung auf Beschr¨ankten Gebieten[D].D T¨ubingen,1994
[2]Li M R.Estimates for the life-span of solutions of semilinear wave equations.CPAA,2008,7(2):417-432
[3]Li Mengrong,Lin Yuju,Shieh T H.The space-jump model of the movement of tumor cells and health cells. Abs Appl Anal 2014,2014:Article ID 840891
[4]Li M R.On the semilinear wave equations.Taiwanese J Math,1998,2(3):329-345
[5]Duan R,Li M R,Yang T.Propagation of singularities in the solutions to the Boltzmann equation near equilibrium.Math Models Methods Appl Sci,2008,18(7):1093-1114
[6]Li M R,Tsai L Y.On a system of nonlinear wave equations.Taiwanese J Math,2003,7(4):555-573
[7]Li M R,Tsai L Y.Existence and nonexistence of global solutions of some systems of semilinear wave equations.Nonlinear Anal,2003,54:1397-1415
[8]Li Mengrong,Pai Jente.Quenching problem in some semilinear wave equations.Acta Math Sci,2008,28B(3):523-529
[9]Li Mengrong.On the generalized Emden-Fowler equation u′′(t)u(t)=c1+c2u′(t)2with c1≥0,c2≥0. Acta Math Sci,2010,30B(4):1227-1234
[10]Shieh T H,Li M R.Numerical treatment of contact discontinuously with multi-gases.J Comput Appl Math,2009,230(2):656-673
[11]Li M R,Lin Y J,Shieh T H.The flux model of the movement of tumor cells and health cells using a system of nonlinear heat equations.J Comput Biology,2011,18(12):1831-1839
[12]Li M R,Lin Y J,Shieh T H.The space-jump model of the movement of tumor cells and health cells.Abs Appl Anal,2014,2014:Article ID 840891
[13]Li M R,Shieh T H,Yue C J,Lee P,Li Y T.Parabola method in ordinary differential equation.Taiwanese J Math,2011,15(4):1841-1857
[14]Bellman R.Stability Theory of Differential Equations.New York:McGraw-Hill,1953
[15]Li M R.Blow-up results and asymptotic behavior of the Emden-Fowler equation.Acta Math Sci,2007,27(4):703-734
[16]Lin T J C,Li M R,Lee Y S.Taiex index option model by using nonlinear differential equation,Math Comp Appl,2014,19(1):78-92
[17]Li M R.On the local existence and uniqueness of weak solutions for Emden-Fowler type wave equation t2utt-uxx=|u|p-1u in one space dimension.Electronic Journal of Differential Equations,2015,to appear
[18]Shiah Y C,Li M R.The Solution to an Elliptic Equation for Performing Exact Volume I5tegral Transformation in the 3-D BEM Analysis.Engineering Analysis with Boundary Elements,2015,54:13-18
[19]Shieh T H,Li M R,Li Y T,Chen M C.A Comparative Study of Flux Limiters Using New Numerical Methods in Unsteady Supersonic Flows.Numerical Heat Transfer,Part B,2015,67(2):135-160
∗Received April 28,2014.This work is financed by NSC,Metta Education,Grand Hall Company and Auria Solar Company.
 Acta Mathematica Scientia(English Series)2015年5期
Acta Mathematica Scientia(English Series)2015年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ALL MEROMORPHIC SOLUTIONS OF AN AUXILIARY ORDINARY DIFFERENTIAL EQUATION AND ITS APPLICATIONS∗
- APPROXIMATION OF COMMON FIXED POINT OF FAMILIES OF NONLINEAR MAPPINGS WITH APPLICATIONS∗
- SOME COMPLETELY MONOTONIC FUNCTIONS ASSOCIATED WITH THE q-GAMMA AND THE q-POLYGAMMA FUNCTIONS∗
- SUB-ADDITIVE PRESSURE ON A BOREL SET∗
- AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
- ORBITAL INSTABILITY OF STANDING WAVES FOR THE GENERALIZED 3D NONLOCAL NONLINEAR SCHR¨ODINGER EQUATIONS∗
