基于宏程序的数控车床编程方法研究

陈农娣

（广东省工业高级技工学校 广东韶关 512005）

基于宏程序的数控车床编程方法研究

陈农娣

（广东省工业高级技工学校 广东韶关 512005）

本文主要针对宏程序的数控车床编程的方法展开了研究，对相关的数学理论作了详细的介绍，并提出了一系列的编程方法和技巧，以期能为有关方面的需要提供有益的参考和借鉴。

宏程序 数控车床 编程方法

由于数控技术没有直接可调用的指令，在一些比较特别的编程中就需要宏程序进行工作。而宏程序具有通用性强、程序短、效率高、检查和修改方便等优点，在数控车床的编程中逐渐得到了广泛的应用。基于此，本文就宏程序的数控车床编程的方法进行了研究，相信对有关方面的需要能有一定帮助。

1.相关数学理论介绍

1.1 特征曲线方程

以椭圆曲线方程为例，x，y为直角坐标系的横坐标和纵坐标，a，b为长短轴，θ为椭圆上任意一点与原点的连线与x轴形成的夹角。

需要注意的是在数控车床编程中，z，x为编程坐标系的横坐标和纵坐标，故直角方程要进行相应变换，即此处x表示半径值。

在椭圆方程中，a若在x轴方向上，b在z轴方向上，则方程应变为：即长短轴与坐标轴存在一一对应关系。

关于如何选择坐标系的问题，一般情况下建议采用直角坐标系，因为其符合我们编程坐标的轴数。但当已知起点和终点对应坐标原点的夹角时，应采用参数坐标系。因此已知条件不同，选择的坐标系不同。

1.2 坐标的平移及坐标的变换

1.2.1 坐标的平移问题

首先要确定坐标坐标平移前后的原点。其次，找出平移前的坐标原点与平移后的坐标原点存在的关系。最后进行一次换算即可。

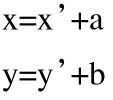
上式即一点在坐标系平移前后之坐标关系式。

1.2.2 坐标的旋转问题

首先要明确旋转的角度，然后根据矢量叠加原理，确定

变换方程即可。

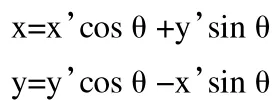
上式即为经过旋转θ角后在直角坐标系中某一点坐标的关系式。

1.2.3 坐标平面内任意变换问题

若是坐标变换中，既存在平移变换，又存在旋转变换，建议优先进行平移变换再进行旋转变换，符合由简单到复杂的原则。

2.编程方法与技巧

2.1 特征曲线宏程序的使用步骤

2.1.1 选定自变量。

一般有以下两种情况：

（1）若已知标准方程，非圆曲线中的X和Z坐标均可以被定义成为自变量，一般选择变化范围大的一个作为自变量。但一旦给定起点和终点的已知条件，则应选择已知条件较多的该轴坐标为自变量。

（2）参数方程一般只有一个变量，所以这个变量就是自变量。

2.1.2 确定自变量变化范围。

值得注意的是，必须明确该坐标值的坐标系是相对于非圆曲线自身的坐标系，其起点坐标为自变量的初始值，终点坐标为自变量的终止值。

2.1.3 进行函数变换，

确定因变量相对于自变量的宏表达式。在标准方程中因为存在根号，所以因变量有正负两个，但是根据图纸可以直接判断取舍一个。函数变换得：，舍正取负。在参数方程中，因为X和Z分别对应同一个自变量，所以不用进行函数变换。

2.1.4 进行坐标变换

根据※1.2坐标系转换，将自身坐标系转换成编程坐标系 （工件坐标系）的过程。这样，才可以在机床上实现正确加工。

2.1.5 利用WHILE/DO循环语句完成宏程序编制。

一般格式为：

需要注意的是，【循环体】包括函数变换、刀具进给和自变量自增三部分。

刀具进给一般采用G01指令。自变量自增（减）目的是为了使循环体得以循环，例如x=x+1，自增（减）值可以是1以外的数字，数值越大，步距越大，加工精度越低，数值越小，步距越小，加工精度越高。精度越高，数控系统运算量越大，进给速度越慢，加工效率越低，因此必须根据加工要求合理选择步距。

下面笔者以WHILE/DO语句编写一段椭圆加工程序。

2.2 特征曲线实例编程

2.2.1 标准椭圆宏程序编程

加工图1所示椭圆轮廓，棒料Φ45，编程零点放在工件右端面。

分析：

（2）根据已知条件令Z为自变量。

（5）因为编程零点放在工件右端面，所以必须将椭圆中心变换至编程零点，根据平移公式得出：x=x'；z=z'-60

（6）编写WHILE/DO语句如下：

图1

2.2.2 抛物线宏程序编程分析图2：

（1）已知该抛物线方程为：。令Z为自变量。

（2）根据已知条件，自变量Z变化范围在自身坐标系中为【1，15.626】。

放眼全省，玉溪市全面落实河（湖）长制为重点，建立覆盖全流域的责任体系，坚决打好新时代抚仙湖保卫战；大理州认真总结洱海流域水环境保护治理工作经验，把“生态+”的理念融入全州产业发展……“绝不以牺牲环境为代价来发展经济”，成为云南各族群众在改革开放进程中的共识。

（3）函数变换：。因为x在原点下方，舍正取负。

（4）因为编程零点放在工件右端面，所以必须将曲线中心变换至编程零点，根据平移公式得出：x=x'+20；z=z'-25.626

（5）编写WHILE/DO语句如下：

图2

2.2.3 斜椭圆宏程序编程分析图3：

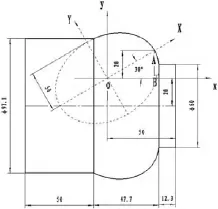
图3

（1）根据已知条件令θ为自变量。因为起点和终点不在同一象限，而且x、y不存在一一对应函数关系，故不能以x或y为自变量，而应该以θ为自变量。

（2）自变量范围需要通过计算求得。根据参数方程x=a*cosθ或y=b*sinθ，只要知道起点和终点的x或y的的坐标值，就可以求得起始角和终止角。

已知在xoy坐标系中，计算得到：

起点x=50-12.3=37.7，y=60/2-20=10，

终点x=97.1/2-20=28.55y=47.7+12.3-50=-10；

在XOY坐标系中，分别计算起点和终点的X坐标值（根据※1.2坐标系转换公式）

起点X=xcos30°+ysin30°=37.7*cos30°+10*sin30°=37.649；

同理，终点X=5.6125；

将计算出的起点和终点值带入公式 x=a*cosθ，求得起始角θ1=-19.741o和终止角 θ2？=81.93o；故自变量 θ 范围为［-19. 741，81.93］。

（4）根据已知得到椭圆参数方程：x=40*cosθ，y=30*sinθ。

（5）因为编程零点放在工件右端面，所以必须将椭圆中心变换至编程零点，根据平移公式得出：x=x'+20；z=z'-50；

（6）编写WHILE/DO语句如下：

结语

综上所述，宏程序是数控系统的一种扩展功能，具有通用性强、程序短、效率高、检查和修改方便等优点，在数控车床的应用中能有极大的帮助。而本文就针对宏程序的数控车床编程的方法作了系统的探讨，旨在能为数控车床技术的发展进步提供帮助。

［1］程启森、张俊.数控车床非圆曲线宏程序编程优化处理［J］.煤矿机械. 2014（07）.

［2］罗根云、于小莎.浅谈数控车床编程中宏程序的巧用［J］.科技资讯. 2010（11）.