应用FIR滤波器消除天津数字地震记录中的干扰
许 可,刘瑞瑞,孔繁旭,朱 宏
(天津市地震局,天津 300201)
0 引言
在数字地震观测系统记录中,除了记录到真实的地震信号外,还记录到很多干扰信号。这些干扰信号严重影响了观测资料的质量需要加以排除[1]。随着信息化社会的到来,计算机和微电子技术的迅速发展,数字信号处理的理论、算法以及实现手段都得到了全面的进步,数字滤波器作为数字信号处理技术的一个重要工具,可用来过滤数字信号。因此,在处理数字地震观测记录中,可以利用滤波器来提取有用信号并抑制干扰信号。这是数字地震资料的分析和处理的重要内容。Matlab是一种面向科学与工程数值计算的计算机软件,工具箱中包含了各种经典和现代数字信号处理技术,能实现各种数字滤波器的设计[2]。本文给出了FIR(有限冲激响应)数字滤波器的Matlab设计方法,并给出了应用这种方法消除天津数字地震记录中干扰的应用实例。
1 FIR数字滤波器的原理与设计
1.1 FIR滤波器的原理[3]
有限冲激响应FIR数字滤波器的单位冲激响应h(n), 是有限长的 0≤n≤N-1 , 长度为 N,(阶数为N-1)的FIR系统函数为:

式(1)中 X (z)、 Y(z)分别为输入 x(n)和输出 y(n)的z变换,h(n)为滤波器的脉冲响应,该式表示:滤波器的脉冲响应h(n)在n=0,1,…,N-1的有限个点(N个点)上有值。
可得FIR滤波器的系统差分方程为:

因此,FIR滤波器又称为卷积滤波器,频率响应表达式为:
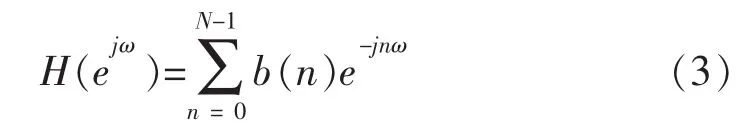
滤波器在通带内具有恒定的幅频特性和线性相位特性。当FIR滤波器的系数满足下列中心对称条件: b(n)=b(N-1-n)或 b(n)=-b(N-1-n)时,滤波器设计在逼近平直幅频特性的同时,还能获得严格的线性相位特性。线性相位FIR滤波器的相位滞后和群延迟在整个品带上是相等且不变的。对于一个N阶的线性相位FIR滤波器,群延迟为常数,即滤波后的信号简单地延迟常数个时间步长。这以特性使通带频率内信号通过滤波器后仍保持原有波形形状而无相位失真。
1.2 FIR滤波器窗函数方法
FIR滤波器主要的设计方法有窗函数法、最优化设计法、约束最小二乘逼近法、升余弦函数法。本文采用窗函数法设计FIR滤波器。如果希望的理想频率响应函数为Hd(ejω),则其对应的单位脉冲响应为:
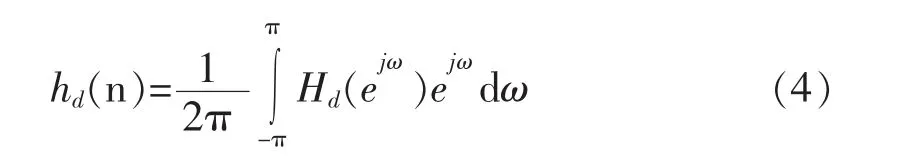
窗函数设计法的基本原理是用有限长单位脉冲响应序列逼近 hd(n)。 由于 hd(n)是无限长序列,而且是非因果的, 所以用窗函数w(n)将 hd(n)截断,得到:

h(n)就作为实际设计的FIR数字滤波器的单位脉冲响应序列,其频率响应函数H(ejω)为:
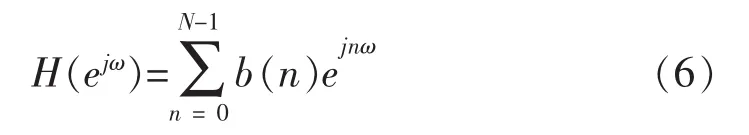
式(6)中N为所选窗函数w(n)的长度。
1.3 基于窗函数的FIR滤波器的设计步骤
(1)对滤波器的理想频域幅值响应进行Fourier逆变换获得理想滤波器的单位脉冲响应hd(n)。
(2)由滤波器的性能指标根据窗函数特点,确定满足阻带衰减的窗函数类型w(n)。
(3)求实际滤波器的单位响应h(n)。
(4)检验滤波器的性能。
本文所用的窗函数是汉宁窗(hanning window),又称余弦窗,主瓣宽是8 π/N,第一旁瓣相对主瓣衰减-31 dB,它可以看做是3个矩形时间窗的频谱之和,或者说是3个sin(t)型函数之和,相当于一个谱窗,向左、右各移动了π/T,从而使旁瓣互相抵消,消除高频干扰和漏能。可以看出,汉宁窗的主瓣加宽并降低,旁瓣则显著减小(如图1),从减小泄露的观点出发,汉宁窗优于矩形窗,但汉宁窗的主瓣加宽,相当于分析带宽加宽,频率分辨率会相应下降。通常来讲汉宁窗的主瓣有较小的旁瓣和较大的衰减速度,是较为常用的窗函数。
2 FIR数字滤波器的Matlab实现
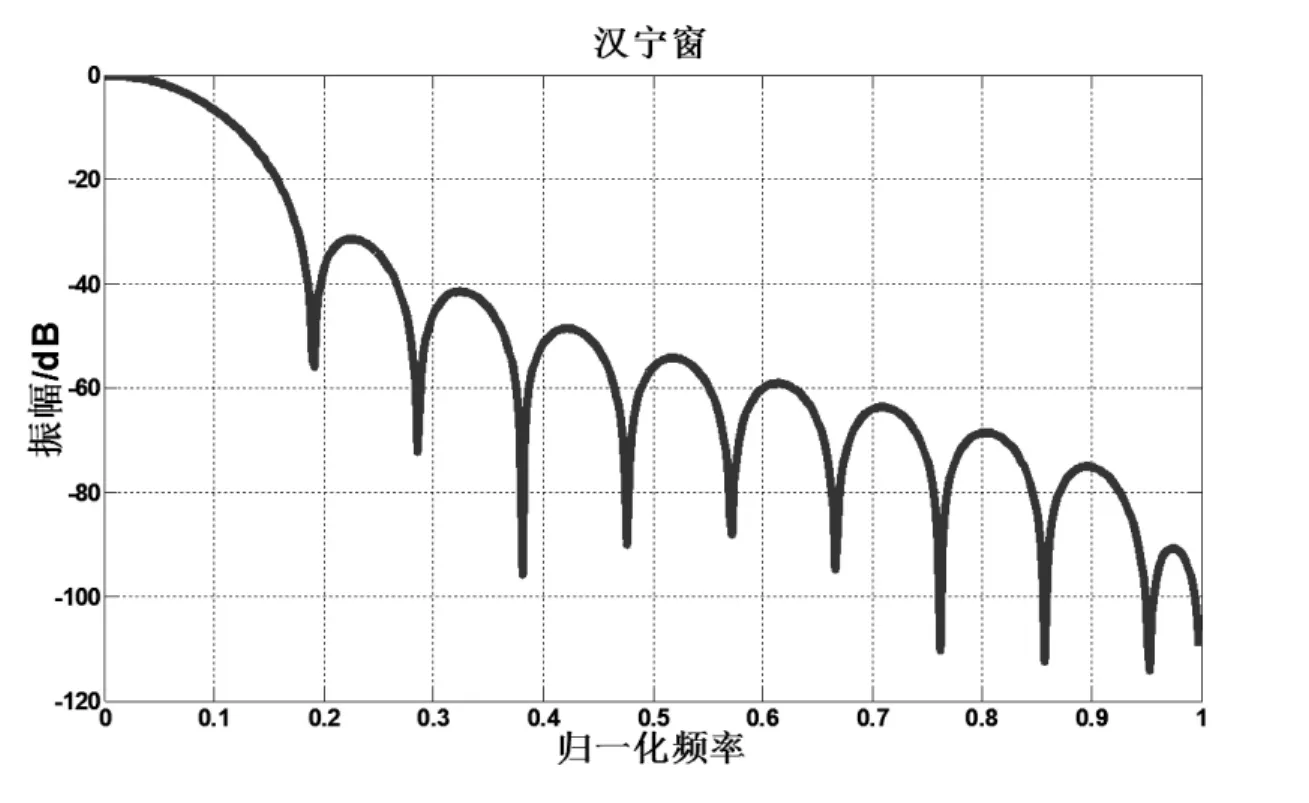
图1 汉宁窗函数的幅频形状Fig.1 The amplitude-frequency shape of the hanning window function
Matlab已经成为数字信号处理应用中分析和仿真的主要工具,它的工具箱中提供了大量设计FIR数字滤波器的函数,这给滤波器的设计带来了极大的方便。下面以基于汉宁窗函数的FIR数字滤波器为例,介绍具体的Matlab实现过程。
(1)确定滤波器的技术指标,主要有采样率Fs,通带边界频率Wp,阻带边界频率Ws,通带波纹Rp,阻带衰减Rs,过渡带宽Wdelta。
(2)根据阻带衰减确定窗函数类型,使过渡带宽近似于窗函数主瓣宽度,则可求得满足性能指标的窗函数的最小长度。如果主瓣宽度为a,则可应用函数N=ceil(a/Wdelta)求得窗函数的最小长度。
(3)用函数 b=fir1 (N, Wn, ‘ftype’, window)求出滤波器的传递函数多项式系数向量b。N为滤波器的阶数,window为窗函数的列向量,其长度为N+1。Wn为滤波器的截至频率。对于带通、带阻滤波器Wn=[w1,w2]。w1和w2分别为带通、带阻滤波器的边界频率。对于低通、高通滤波器Wn=(Wp+Ws)/2。 ‘ftype’为滤波器的类型。
(4)用函数 [H, f]=freqz (b, 1, 512, Fs)分析出所设计的滤波器的幅频特性和相频特性。
(5)用函数 y=filtfilt(b,1)完成对原始信号 x 的滤波得到输出信号y,并进行Fourier变换与原信号进行比较。
3 消除天津数字地震记录中的干扰
天津位于华北平原东北部,与河北省和北京市为邻,东邻渤海,全境绝大部分属华北平原,数字地震记录到的大部分是近震。天津数字地震台网各子台分布在天津18个区县的学校、医院、工厂、村庄等。由于天津东部临近渤海海域,南部是经济和工业发达的地区,人口稠密。因此,经常记录到的波形叠加了高频或低频的成分。针对干扰的不同频率成分,可设计基于窗函数的FIR数字滤波器进行滤波,消除干扰。
2014年3月30日23时11分,天津汉沽发生ML2.3级地震。天津沙井子台北南向,记录到的原始信号中夹杂着多种干扰,掩盖了地震信息。通过快速Fourier变换(fft)分析可知,波形11~45 Hz频段内存在许多高频振动干扰,主要是受人为噪声干扰影响。沙井子地震台位于天津最南部的大港工业区,距离沙井子台1 km处有一个风力发电厂,每天有许多风力发电机运行,地震波形的Fourier变换上有许多比较有规律的高频干扰,如图2。
根据波形干扰的频谱范围特点,可设计带阻FIR滤波器,通带的起始频率w1=11 Hz,截至频率 w2=45 Hz,阻带衰减 Rs=30 dB,过渡带宽Wdelta=0.5 Hz,采样率 Fs=100 Hz。根据上述Matlab实现过程(2),可确定选取的窗函数为汉宁窗,FIR滤波器阶数800。由(4)可得到带阻滤波器的幅频特性和相频特性。如图4。
根据(5)使信号通过滤波器进行滤波。结果显示信号通过滤波器后滤除了高频振动干扰,滤波之前信号被高频干扰所掩盖,滤波之后可以很容易的分辨出地震波的震相。并且滤波后的信号相位无失真,滤波器达到了预期的要求。采用Fourier变换分析滤波后的振幅谱,其中阻带内的频率成分被滤除掉。如图5。
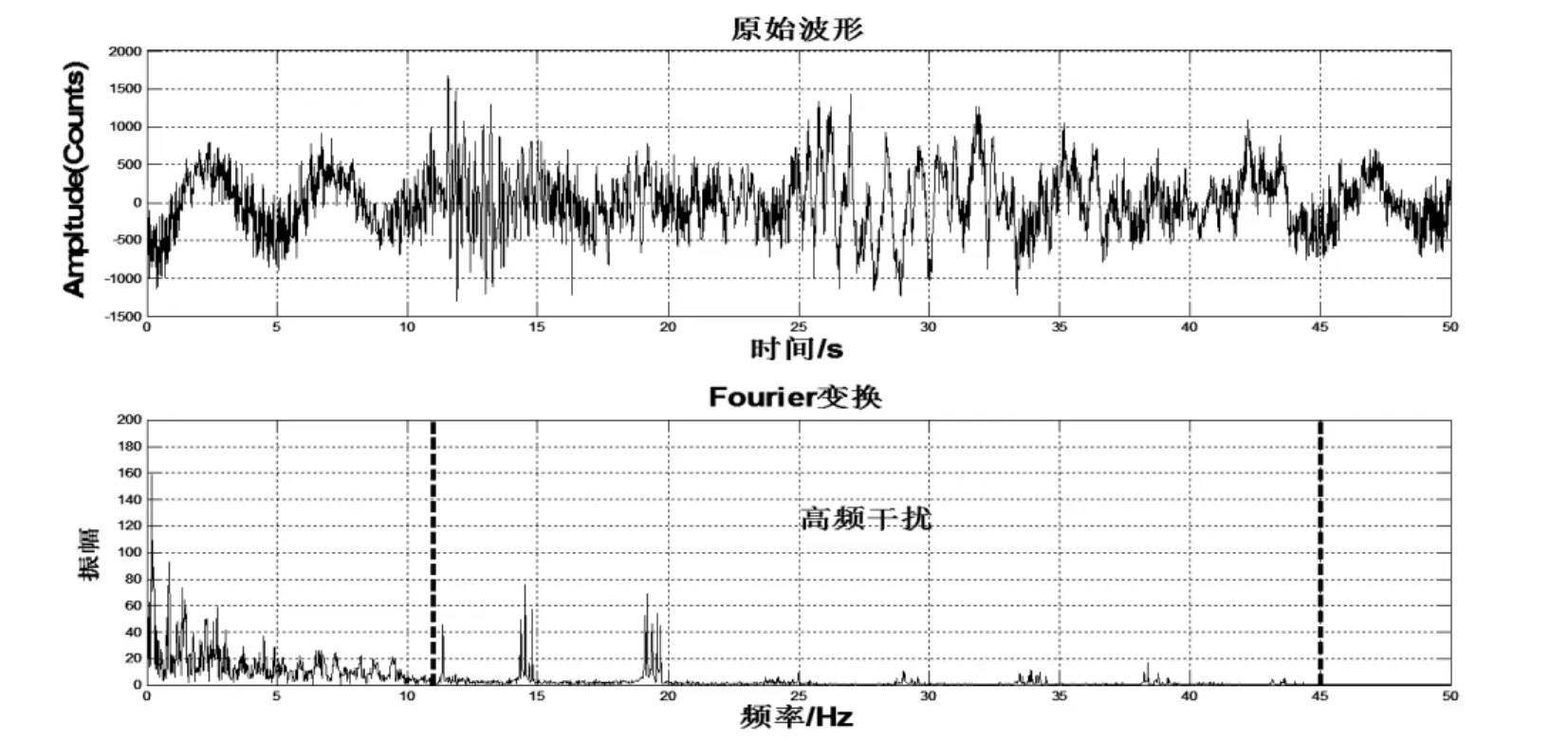
图2 原始波形及Fourier变换Fig.2 The original waveforms and the Fourier transform
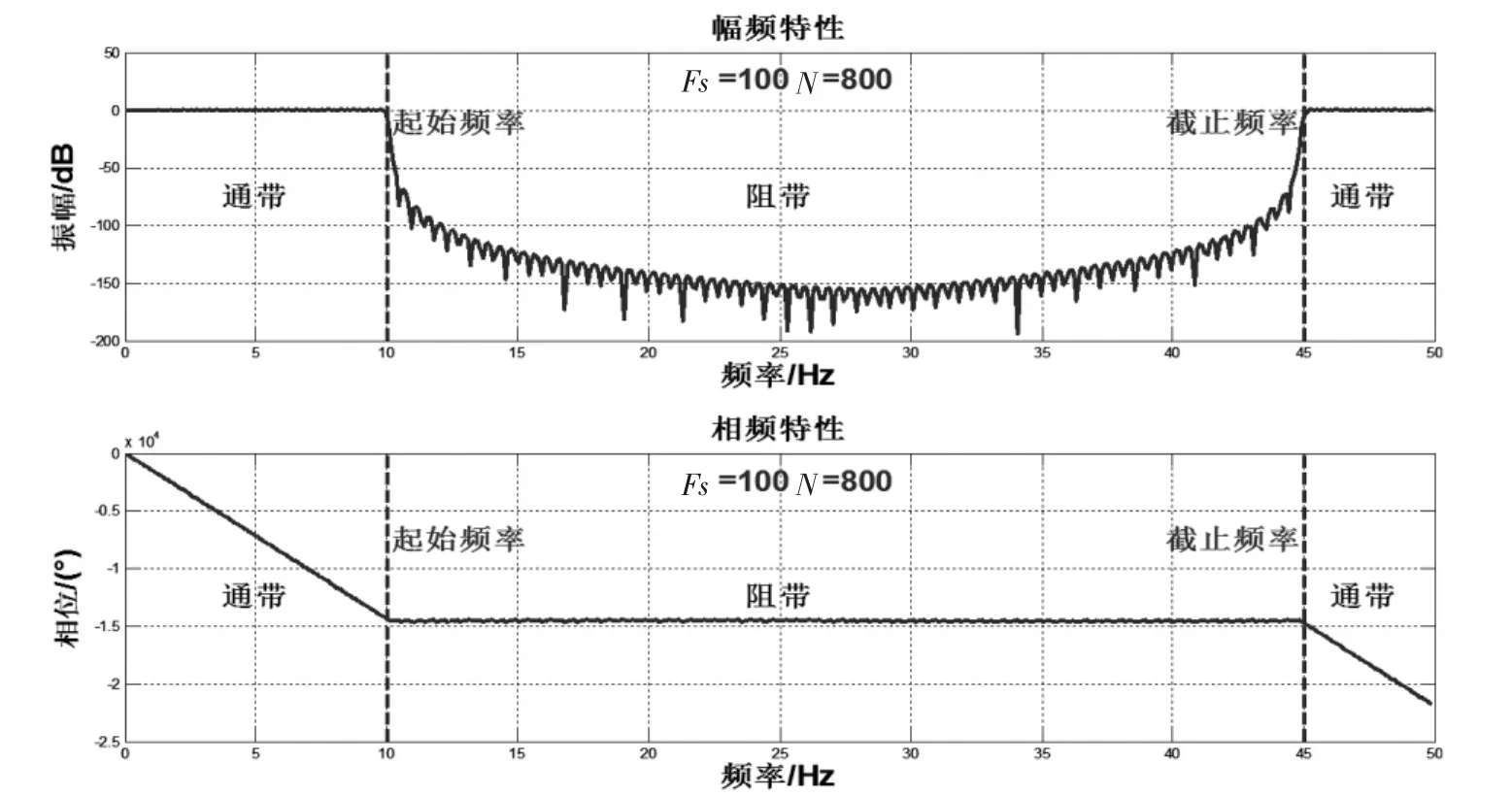
图3 带阻滤波器的幅频和相频特性Fig.3 The amplitude frequency and phase frequency characteristics of Band-stop filter
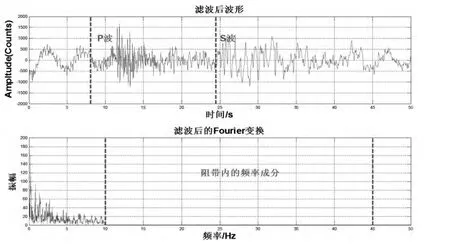
图4 滤波后的波形及Fourier变换Fig.4 The filtered waveforms and the Fourier transform
天津糙甸台经常记录到的波形叠加了低频干扰,波形严重变形,很难分析。可设计高通FIR数字滤波器,通带起始频率为5 Hz,阻带截止频率为3 Hz,过渡带宽为4 Hz,阻带衰减大于30 dB,采样率为100 Hz。滤波器的幅频与相频特性,如图6。
可以看到,该滤波器小于5 Hz的低频部分不能通过,大于5 Hz的高频部分可以通过。较好的滤除了小于5 Hz的低频干扰,清晰的反映出P波、S波的震相特征。图6为原始波形与滤波后的波形对比。
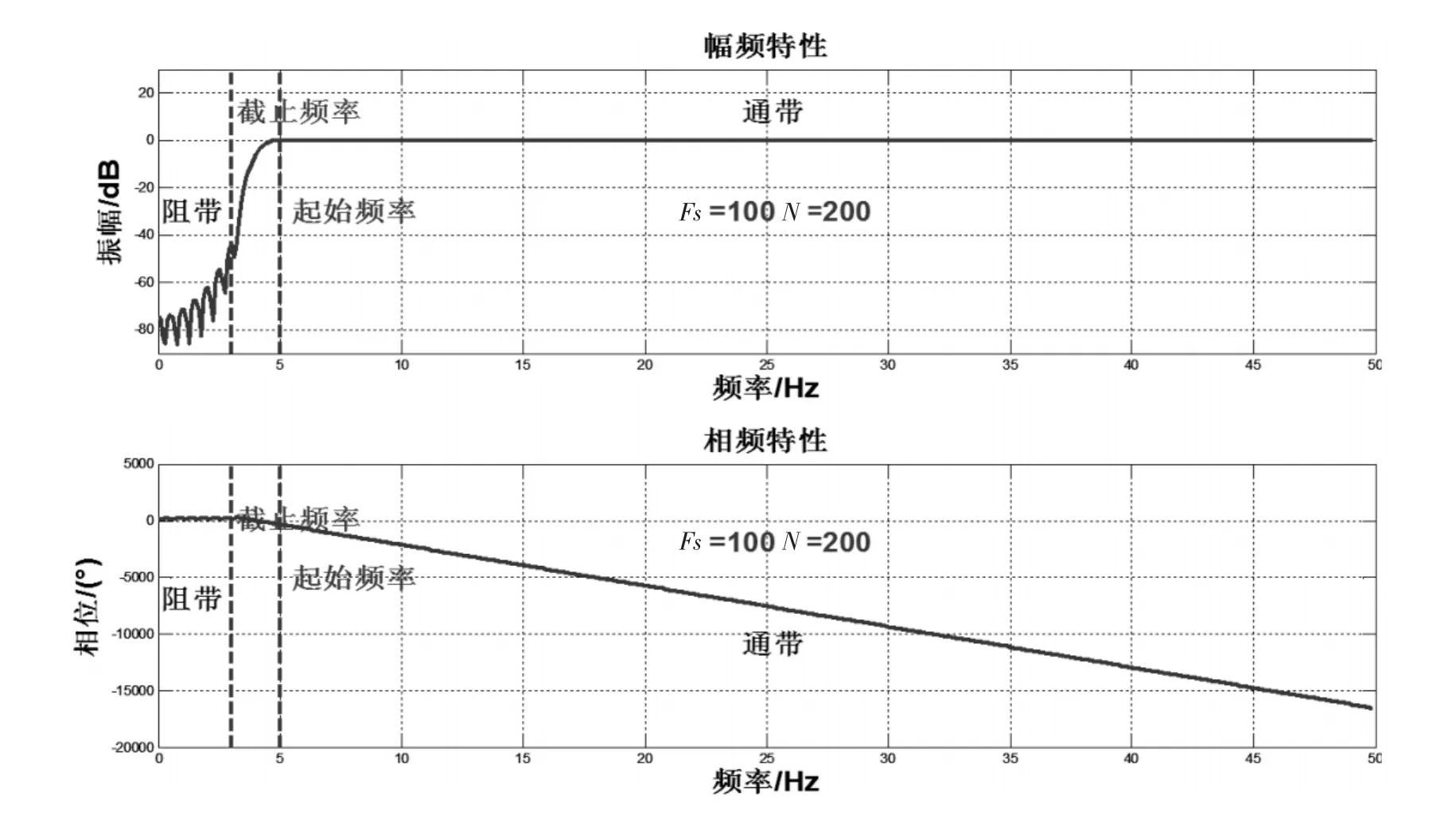
图5 高通滤波器的幅频和相频特性Fig.5 The amplitude frequency and phase frequency characteristics of High-pass filter
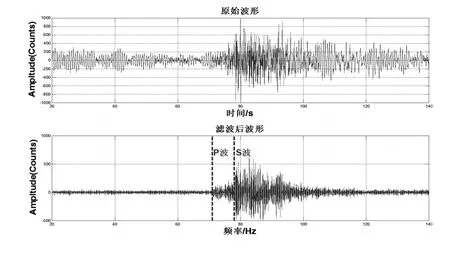
图6 原始波形及滤波后波形Fig6 The original waveforms and the filtered ones
4 结语
随着信息时代与数字技术的发展,数字信号处理己逐渐发展成为当今极其重要的学科与技术领域之一。数字滤波器是数字信号处理的重要基础,在对信号的滤波、检测及参数的估计等信号应用中,数字滤波器是使用最为广泛的一种线性系统。数字滤波器根据其单位冲击响应函数的时域特性可分为两类:无限冲击响应(IIR)数字滤波器和有限冲击响应(FIR)数字滤波器。与IIR数字滤波器比,FIR数字滤波器的实现是非递归的,稳定性好,精度高;更重要的是FIR数字滤波器在满足幅度响应要求的同时,可以获得严格的线性相位。因此,它在高保真的信号处理中可以到广泛应用
本文将FIR数字滤波器应用于排除地震记录中的干扰信号,运用MATLAB语言能容易地设计出满足要求的FIR数字滤波器,设计简单方便,大大减少了工作量。在应用中只需对程序中滤波器的起始频率、截止频率、采样率和窗函数等参数进行修改就可以实现需要的滤波功能,达到较好的滤波效果。综上所述,FIR数字滤波器可以很好的排除地震记录的干扰信号,信号经重构后,可以得到较为理想的曲线,这样既提高了观测资料质量,又易于进一步对资料进行深入准确的处理[4],为今后数字地震资料的分析与应用奠定基础。
[1]李敬,甘延锋,黄友明,等.数字地震记录中干扰波的排除[J].防灾技术高等专科学校学报,2004,6(3):20-25.
[2]万永革.数字信号处理的MATLAB实现[M].北京:科学出版社,2007.
[3]陈杰.MATLAB典[M].北京:电子工业出版社,2004.
[4]曾庆堂,起卫罗,马志刚,等.MATLAB消除腾冲台数字地震记录中干扰波的应用[J].华南地震,2014,34(1): 58-62.
[5]鲁权,邢西淳,李西京,等.泾阳台数字地磁信号的干扰分析及去噪处理 [J].华南地震,2013,33(1):49-54.
[6]肖攀,宋国华,李露露,等.蚌埠地震台测震干扰分析及处理[J].华南地震,2013,33(1):86-92.

