利润约束的关联规则挖掘算法

朱龙

（四川信息职业技术学院 信息工程系，四川 广元628040）

购物篮分析是大数据在零售业的一个崭新应用方向，就是商家希望通过分析每个购物篮子中都装了什么商品，进而通过这些信息来研究顾客们的购买喜好，找出其中暗含的规则，其最终目标就是让超市和生产企业通过大数据挖掘，建立自己产品的竞争优势.购物篮分析中常用的是Apriori算法，它成功弥补了零售业数据分析不足、有价知识提取匮乏的问题，在商家积累的海量数据中，例如零售业数据，其中的知识若经Apriori算法有效分析提炼，可以充分提升商家销售业绩.本文对于Apriori算法原有的支持度和置信度的运算进行了相关调整，设计了新的基于利润加权约束的加权支持度和加权置信度求取方法，并以此为基础对Apriori算法进行改进.

1 Apriori算法

Apriori作为一种有特色的传统算法，根据循序渐进的方式，利用数据库找寻各项之间的联系，并组成关联规则.它的核心是挖掘颖繁项集，输入minsupport，指导频率的阈值，如minsupport＝5%表示用户（超市商家）是对数据库中事务数据概率大于5%的子集感兴趣.

Apriori算法输入最小支持度minsupport后，利用数据库提取出所有产品交易信息，并获得Candidate 1－itemset.随后就可以找到Large 1－itemset，此时将各个Large 1－itemset连接形成Candidate 2－itemset.当候选2项集中的某一项的支持度≥minsupport，则这个候选项就划入到高频项集.

以此类推，已建立的2项集为基础，再找出所有的高频2项集.然后，进一步利用提取出的高频2项集，三三组合，生成候选3项集.重复高频2项集的搜索方法，与minsupport作比较，提取大于minsupport的3项集构成高频3项集.以此类推，直到达到用户的目标为止.

2 利润的约束关联规则数据挖掘

Apriori算法是一种比较有效的关联规则数据挖掘方法，但它以数据库中所有项在挖掘时都是等价的为前提，即权值都为1、所有项的重要程度都一样.但在现实世界中，数据库中的每一项都是一种商品，它们的重要形式不同的.最直接的就是不同的商品带给超市的利润是不同的.若Apriori算法直接进行数据挖掘，则价值高的大件商品会因为出现频率小（购买数量少）被算法认为不重要而丢掉，对关联规则的数据挖掘结果造成不利影响.

2.1 利润加权阈值的设计

利润是超市经营决策者所关心的最重要的问题.利润＝商品销售数量×商品利润率，记为P，利润P越大，越受到超市的重视.因为超市中商品销售利润率大多数情况下是比较固定的，不会随着客户购买商品的多少而变化，所以一种商品的销售数量也可通过利润P的值反映出来.

令项目权重集为

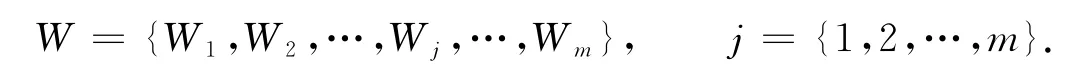
式中：W为商品的权重，由一段时间内的商品利润计算得到.商品利润建立的权重，如表1所示.

表1 权重对照表Tab.1 Weight comparison table

2.2 归一化处理项目权重集

对于MINWAL（O）算法可能存在加权支持度大于1的情况，对权重集合W＝｛W1，W2，…，Wj，…，Wm｝实施归一化处理.

原来的权重集W可以用归一化权重集代替.为了表示方便，归一化的项目权重集依旧用W表示，即

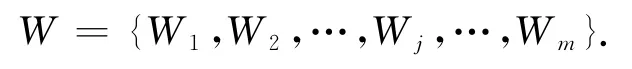
式中：W1＋W2＋…＋Wj＋…＋Wm＝1.

2.3 布尔向量的获取

重新统一统计超市信息库的原始交易记录，交易记录如表2所示.在购物篮分析的传统方法中，仅是根据购买与否进行“1”和“0”状态的归一化处理.即对于在超市记录的某种商品销售数据中，若客户购买，记为“1”；若无购买，则记为“0”.原始记录依照此方法获得的布尔向量，如表3所示.

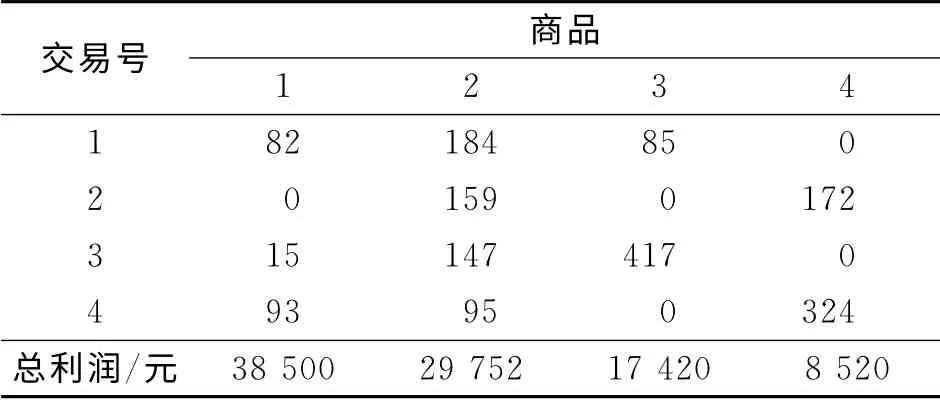
表2 超市商品的交易记录Tab.2 Trading recordings of supermarket goods

表3 传统的布尔向量Tab.3 Traditional boolean vector

上述处理过程的缺点是没有考虑每件商品的购买数量，认为大批量销售和单件销售的影响是一样的，将销售100件和1件等同处理.依照这种方式获得的布尔类型数据，准确度值得商榷，获得的知识有可能存在大量失真.首先，将某样产品每一次的交易量除以在销售中最多卖出的数量，如表2中商品1，4次交易中最大的销售数量是93件，则商品1的各条记录中在销售数量的字段都除以数值93，可得到新的4次交易数值为0.88，0，0.16，1.00.按照此方式，对表1中的权重数据利用式（1）实施处理，数据统计后的结果，如表4所示.表4中：最后一行数据是新得出的.

当某项目（某种商品）归一化后，若其数值大于或等于该商品的利润加权阈值，布尔值转换表中的对应位置结果记为“1”，以次标识用户对该商品感兴趣，以此作为后续挖掘关联规则数据的属性；若数值小于利润加权阈值时，布尔值转换结果记为“0”，作为后续挖掘关联规则数据的属性.根据这种规则，以商品1为例，它的权重W1等于0.4.因此，表4中商品1的交易号1的第1行记录是0.881 7（＞0.400 0），布尔变量取值为1；而交易号2，3记录的值分别为0和0.161 3，它们都小于0.400 0，对应的布尔变量都取值为0；交易号4的记录大于权重，以此布尔变量取值为1.依此类推，对表4中的数据实施布尔向量化，可以得到通过利润加权阈值处理后的布尔记录表，如表5所示.相比较于表3，可见表5的记录更加简化.

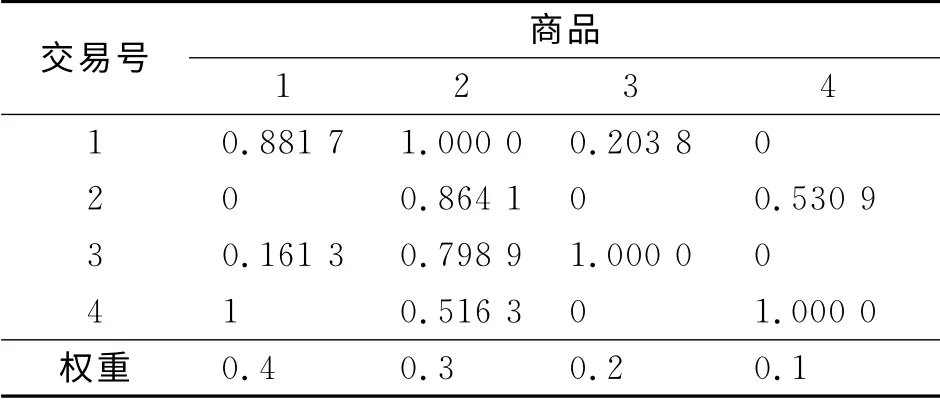
表4 归一化后的商品交易记录Tab.4 Commodity trading records after normalization

表5 利润加权处理后的布尔向量Tab.5 Weight processing of Boolean vector

2.4 加权支持度和加权置信度

由于每个领域工程都已经有权重数据，Apriori算法中的运算需要进行改进，通过重新定义来满足需要.以利润加权关联规则数据挖掘中的加权支持度和加权置信度为基础.令数据库中项目集X的交易记录中的数量集合为S（X），交易总数取值为n.

对于项目集X｛x1，…，xp｝，其加权支持度定义为

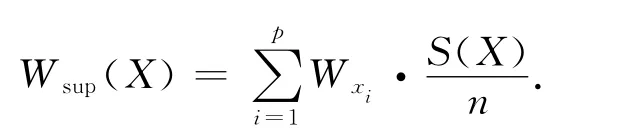
将最小加权支持度（Wminsupport）设定成用户设定的原始最小加权支持度，假设计算出的加权支持度Wsup（X）≥Wminsupport，则算法称X是“加权大项集”.

3 算法设计

对于Apriori算法，若求取高频项集时，它的全部子集都属于高频项集；但是若项目添加了权重信息，上述的性质不再有效，大项集的某些子集可能并不属于大项集.

3.1 算法描述

算法的输入：数据库D，每个商品项目的权重Wm，用户设定的Wminsupport，用户设定的最小加权置信度（Wminconf）.

步骤1将各项目权重排除在外，基于布尔型关联规则挖掘技术确定高频项集，当项集的支持度大于或等于Wminsupport时，提取出该项集.如果一种商品十分受欢迎，数据挖掘过程中，加权的作用是突出更加它的受欢迎程度，即加权高频项集是包含在这些未加权处理的项集的子集中，该项集就是加权高频项集的超集.

步骤2对超集中包含的所有项集实施挖掘，求出每个超集中每个项集的加权支持度，把大于或等于（Wminconf）的项集取出作为加权大项集；对去除项集后的超集继续扫描，直至找出超集中的所有的加权大项集.在第二步数据挖掘中，因为加权高频项集包含在这些未加权项集的子集中，因此，无需再次扫描超市的商品交易数据库，只需超集乘上每项所对应的项集权重即可.

步骤3基于加权大项集改良形成加权关联规则.最大的改良之处在于经过加权处理后提取出的加权大项集形式未发生改变，因此，可以使用布尔型关联规则产生加权大项集的关联规则.

输出：超市商品的加权关联规则.

3.2 算法的数据挖掘流程

B为数据库，Lk是高频k的项集，Ck是候选k项集，T临时项集，项目的权值属性定义为W＝｛W1，W2，…，Wj，…，Wm｝.算法的运行过程为

定理1 设X为项集，C1和C2分别为单调性约束和非单调性约束.

1）如果C1（X）＝不正确，那么∀Y⊆X，C1（Y）∧C2（Y）＝不正确，即X的任何子集都不同时满足C1和C2；

2）如果C1（X）＝正确，C2（X）＝正确，则存在Y⊆X，使得C1（Y）∧C2（Y）＝正确；

3）如果C1（X）＝正确，C2（X）＝不正确，则存在Y⊆X，使得C1（Y）∧C2（Y）＝正确.

证明 如果C1（X）＝不正确，很显然有∀Y⊆X.根据单调约束的性质，C1（Y）＝不正确，于是不管C2（Y）的值如何，C1（Y）∧C2（Y）＝不正确.

4 试验结果分析

关联规则挖掘的目标是挖掘出暗含在数据库中的知识，为了测试基于利润的约束的关联规则挖掘算法的特性，选用了将其他算法与Apriori算法进行比较，如图1所示.图1中：纵坐标是数据挖掘获取的高频项集；横坐标是不同的最小支持度的取值.对于各个不同的最下支持度，每个横坐标点左边柱体是Apriori算法数据挖掘所算出的最有意义的项目，右边柱体是算法在该的最小支持度下挖掘出的有效项集数量.由图1可知：其他算法（右边柱体）和Apriori算法（左边柱体）直接按对比明显，提取出的有价值项集数目精简明显.

假设非单调性约束C1：max（S.cost）≤min（S.price）；单调性约束C2：total（S.price）≥100；最小支持度为20%（表1）.

1）求出数据库频繁1项集（按支持度由大到小排列）：D，E，B，A，C.

2）C2（DEBAC）＝不正确，得出N值至少大于等于2.

3）C1（D）＝正确，C1（E）＝正确，C1（B）＝正确，C1（A）＝正确，C1（C）＝正确.

以A为例，D的支持度最大，没有必要生成D的条件数据库，因为它的支持度最大，已经没有前缀项了.

4）求出A的条件数据库，其投影事务在原数据库中分别为（项按支持度由大到小排列）：｛DEB，DB，E，DE，DEB｝.

5）求出频繁1项集：D，E，B.由于DEBA为4项，大于N的值，因此，后面考虑继续生成各项的条件数据库.

6）C1（DEBA）＝不正确；C1（DA）＝正确；C1（EA）＝正确；C1（BA）＝不正确.

7）由于DEA的子集除了DEA是3项外，其余为≤2，经检查，均不满足C2，最后输出满足C1∧C2的A的条件数据库中的频繁项集为DEA.

图1 算法比较Fig.1 Algorithm comparison

5 结束语

针对Apriori算法在实际应用中的不足，设计了基于利润的约束关联规则挖掘算法，对数据库的原始数据实施了利润约束修正，增加了利润加权阈值，有效提升数据挖掘算法的知识挖掘性能.到目前为止，大部分算法还只是一种挖掘，所以其算法还是不够完善，而新算法不但能进行约束的挖掘，还能进行另一种算法，分别是单调性和非单调性.

［1］HAN Jia－wei，KAMBER M.数据挖掘概念与技术［M］.北京：机械工业出版社，2001：132－156.

［2］陈奇，俞瑞钊.关联规则采掘综述［J］.计算机应用研究，2000，17（1）：1－5.

［3］李兴良，陈湘涛.数据挖掘中关联规则算法的研究［J］.计算机工程与科学，2007（12）：111－116.

［4］MICHAEL J A B，GORDON S L.数据挖掘：客户关系管理科学与艺术［M］.北京：中国财政经济出版社，2004：10－52.

［5］黄健斌.基于关联规则挖掘的入侵检测技术研究［D］.重庆：重庆大学，2007：13－19.

［6］王德兴，胡刚，刘小平.基于概念和Apriori的关联规则挖掘算法分析［J］.合肥工业大学学报：自然科学版，2006，29（6）：69－702.

［7］杜海涛，陈定方，张波.基于关联规则的超市购物篮分析方［J］.湖北工业大学学报，2008，23（4）：15－18.

［8］薛红，聂桂华.基于关联规则分析的购物篮分析模型研究［J］.北京工商大学学报：自然科学版，2008，23（4）：15－18.

［9］黄嘉满.面向零售业的关联规则挖掘的研究与实现［D］.上海：上海交通大学，2007：4－45.

［10］冯瑶.基于零售业的数据挖掘技术和关联规则算法的改进研究［D］.天津：河北工业大学，2006：31－43.

［11］谢小兰.应用数据挖掘技术提高决策能力的研究［J］.商情，2011（47）：139－142.

［12］张文献，陆建江.加权布尔关联规则的研究［J］.计算机工程，2003，29（9）：55－57.