风洞层流风场中的WDPSS-8机器人系统的末端位姿偏移及补偿

王梓，郑亚青

（华侨大学 机电及自动化学院，福建 厦门361021）

近年来，绳牵引并联支撑系统被广泛应用于风洞飞行器模型的支撑机构，该支撑系统很适合测量飞行器模型的气动导数［1］.然而，索系结构作为一种典型的柔性结构体系，由于其只能承受拉力，横向刚度较小，在绳索与风场的耦合作用下会引起绳索的变形，可能导致模型位姿偏离既定值，需要对位姿进行补偿.法国航空研究局（ONERA）支持的预研项目SACSO 用九根绳索牵引着模型在立式风洞中进行风洞自由飞行实验［2－3］，该项目研究了绳索对风洞中层流风的影响［4］.但尚未见到有关绳索在风洞层流风中的风致变形行为的文献报道.郑亚青等［5－6］对WDPSS－8系统应用于飞行器模型静态测力低速风洞试验的支撑系统开展了研究，指出该系统可以用于强迫振荡实验提取模型的气动导数.该项目也通过ANSYS软件对绳索在均匀流速为35m·s－1风速下进行流固耦合行为的研究［7－9］，但在建模时忽略了飞行器模型，尚未提到系统末端执行器位姿偏移情况，且尚未见到对系统位姿补偿的研究.本文对风洞层流风场中的WDPSS－8机器人系统的末端位姿偏移及补偿进行研究.

图1 索系在风洞试验段中的位置Fig.1 Location of cable system in the test section of a wind tunnel

1 WDPSS-8系统的相关参数

利用WDPSS－8系统对飞行器模型开展一系列静态实验，相关参数参照文献［6］.索系在风洞试验段中的位置，如图1所示（略去飞行器模型）.风洞试验段空气柱为长方体，其内部的表面由绳索和飞行器的外表面围成，风吹方向如左边箭头所示，平行于全局坐标系的Z0轴.1～8分别代表第i（i＝1，…，8）根直径为4mm 的绳索.

利用Matlab对系统进行运动学逆解和静力学分析，为仿真提供绳长和绳拉力参数.飞行器模型由8根绳索牵引置于空气域，主要由机身和两侧机翼组成，其机身长为270mm，翼展长为285mm，质量为20kg.

设X＝［XPXang］T 为飞行器缩比模型的参考点P相对于坐标系OXYZ的位姿.XP为P的位置坐标：（xP，yP，zP）T；Xang为坐标系PxPyPzP相对于坐标系OXYZ的姿态坐标：（φP，φY，φR）T［10］.

由于8根绳索在固定坐标系OX0Y0Z0中的空间位置相异，为了讨论不同绳索倾角和风向角对索系结构风振耦合响应的影响，引入绳索倾角α、风向角β、索表面点位置角θ，如图2所示.

图2 绳索倾角、风向角及 索表面点位置角Fig.2 Inclination angle of the ropes wind direction angle and position angle of the cable surface points

2 索系流固耦合分析模型的建立

通过ANSYS WORKBENCH 的CFX 平台对层流风场中的WDPSS－8系统进行流固耦合分析，包括流场网格模型（流体模型）、绳索有限元模型（固体模型）及飞行器模型（因变形小作刚体处理）.在流体模型中，风场环境取温度为25 ℃，密度为1.185kg·m－3，粘性系数为1.831kg·（m·s）－1的不可压流场，以及平均风速v分别为35，60，100m·s－1的层流风场.

假定绳索为各向同性材料且处于线性弹性范围内，其弹性模量为0.206TPa，泊松比为0.3，则绳索的弹性极限为0.261TPa，密度为7 000kg·m－3.由于绳索在重力作用下并非一条纯直线形式，而是悬链线形式.经过计算，0.9m×1.1m 的WDPSS－8系统跨度小，绳索的悬链模型与直线模型重合.因此，索长计算时不考虑悬链线变化，近似为滑轮与绳索接触点及飞行器模型与绳索接触点之间的直线距离；绳索两端的力要考虑因绳索重力而产生的力矩作用，但因无需考虑绳索因形状变形而对力矩的影响，绳索可采用直线模型进行建模.对于固体域网格的划分，由于常用于仿真绳索的Link单元为线单元，不能进行流固耦合分析，故采用体单元进行仿真.但由于体单元为非线性单元，不能设置其特性为只受拉不受压，预拉力的施加至关重要.根据ANSYS的帮助文件，采用多载荷步的方法对绳索施加预拉力.这里仅考虑耦合分析时，添加的来自驱动系统的外拉力.

对于系统约束的添加，由于动力学模型中柔索与末端执行器之间相互耦合，索端牵引力拖动末端执行器运动，末端执行器的运动又决定了柔索末端节点的位置，必须将飞行器模型建于流固耦合分析模型中，设置为刚体.分析WDPSS－8机构特点，绳索相对于飞行器连接端为球铰链连接，用JOINT－SPHERICAL实现.与绞盘连接一端绳索平动自由度均被约束，只剩转动自由度，可采用DEMOTE－DISPLACEMENT 约束实现.

3 末端位姿偏移及补偿

3.1 动静力特性分析及位姿偏移

3.1.1 层流风场中索系流固耦合变形分析 基于ANSYS／CFX 在风速v分别为35，60，100m·s－1的层流风场中对WDPSS－8系统进行流固耦合分析，在流固耦合分析的后处理阶段，提取索系在吹风前后的最终变形图.绳索的最终变形主要表现为顺风向弯曲（即），其最大变形均发生在上风向绳索中间位置.提取风速为35m·s－1的层流风场中绳索1～8沿绳索长度（D）变化的位移分量（U），如图3所示.由图3可知：绳索倾角α较大的绳索，如绳1，2，7，8形变量相对较大，位移分量UZ值较其他两个分量都大，反映出绳索以顺风向弯曲为主；绳索倾角α较小的绳索，如绳3，4，5，6形变量相对于绳长很小，位移分量均趋于0；由于绳索7，8（图3（g），（h））对称分布在流场中，虽然形变量相对较大，但两绳索长度相等且绳索位移分布相似，可推断其形变量对其共同控制的飞行器模型滚转角φR 没变化；位于上风向的绳索1相对下风向的绳索2（图3（a），（b））形变量较大，且两绳索长度不等，可能影响其共同控制的飞行器模型俯仰角φP.

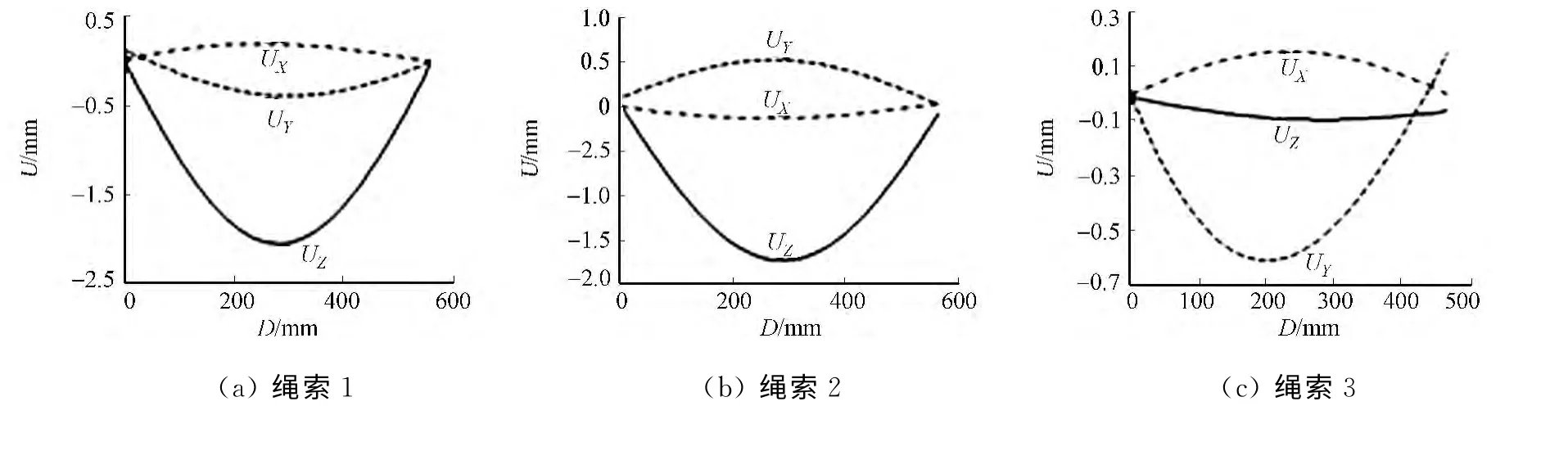
图3 风速为35m·s－1的层流风场作用下索系沿3个坐标方向的变形图Fig.3 Deformation figure of the cable system along the 3coordinate directions in the laminar flow field with 35m·s－1

不同风速层流风场中系统吹风前后绳索内力值变化及其方向分量，如表1所示.表1中：T0，T′分别为吹风前的绳拉力和吹风后的末端绳拉力；v为风速.由表1可知：绳索倾角α较大的绳索内力变化量并不大，而绳索倾角α较小的绳索内力变化量较大；随着风速增加，上风向绳3，4内力增加程度增大，即张得更紧；下风向绳5，6内力减小程度增大，即更加松弛，此现象符合物理意义.

根据吹风后绳索内力各方向分量计算可知：吹风后与飞行器连接端的绳索形状与吹风前的直线模型有一个夹角，即在层流风作用下，绳索发生顺风向弯曲.在35m·s－1层流风场中，此夹角变化范围较小，为0°～0.5°；在60m·s－1层流风场中，此夹角变化范围为0.1°～0.8°；在100m·s－1层流风场中，此夹角变化范围为0.2°～1.8°；弯曲程度最大处发生在绳索倾角α较大的绳索，且绳索7，8弯曲角度一致，绳索倾角α较小的绳索几乎没有弯曲.

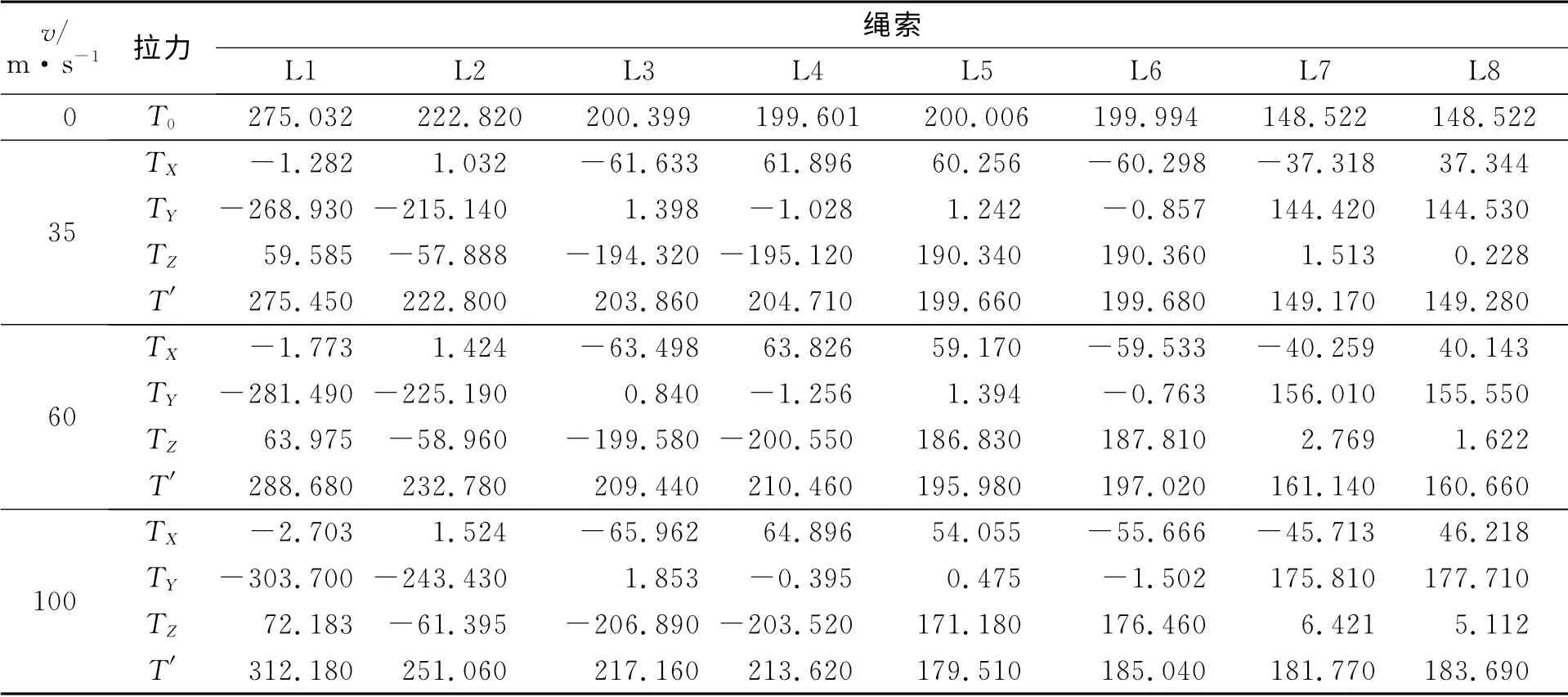
表1 吹风前后绳索内力变化Tab.1 Internal force change of the ropes before and after blowing N

3.1.2 层流风场中的飞行器模型的实际位姿计算 以（xP，yP，zP，φP，φY，φR）表示飞行器模型的坐标系相对于固定坐标系的位姿，当风速为35，60，100m·s－1时，飞行器的实际位姿分别为（0，－0.003，－0.032，0，0，0），（－0.158，－0.262，－0.169，2.1′，0，0.4′），（0.181，－0.655，－0.398，6.6′，0.2′，1.8′）.说明在较大风速风场作用下，模型位姿会发生较大的偏移.由图3绳索变形位移图可知：这是由于吹风后绳索会发生顺风向弯曲，其中，绳索1，2的形变会引起飞行器模型在俯仰角方向的偏离.另外，根据表1可知：吹风后飞行器连接点处绳索方向矢量与吹风前直线模型绳索方向矢量有一个夹角，这将导致吹风后零位姿处模型的结构矩阵JT发生变化.在风速为35m·s－1的层流风场中，吹风后绳索形状与直线模型几乎重合，即结构矩阵JT几乎无变化.因此，根据吹风前系统的零位姿结构矩阵计算得到的绳拉力值可以使飞行器达到既定位姿.在风速分别为60，100m·s－1的层流风场中，吹风后绳索弯曲程度较大以致不能忽略（在100m·s－1层流风场中夹角可达1.8°），导致结构矩阵JT发生变化，尤其是绳索1，2，这反映在吹风后飞行器在俯仰角位姿上产生偏离.

3.2 基于迭代法的WDPSS-8系统末端位姿补偿

由于风洞实验定位精度要求高，对飞行器模型进行逐一定位到期望位姿后再进行吹风实验，考察俯仰、滚转和偏航角变化时的飞行器性能，每次变化量为1°，定位精度为2′.根据上文分析结果，可以看出3种不同风速层流风场作用下飞行器位姿确实发生了变化.由于模型中柔索与末端执行器之间相互耦合，8根绳索的变形相互制约，绳索形状、内力的变化在风速为35m·s－1的层流风场中的综合作用对飞行器位姿并未产生太大的影响.而在风速分别为60，100m·s－1的层流风场中，其综合作用不但引起模型顺风方向偏移，且在俯仰角位姿上的偏离超出定位精度要求，有必要对吹风后飞行器位姿进行补偿.

静态实验中绳索所受的拉力，与末端执行器位姿、绳索方向矢量和系统受力情况有关［4］.飞行器静力学方程可描述为

式（1）中：WR为作用在飞行器模型上的力螺旋矢量；JT为机构的结构矩阵，与绳索方向的位置矢量和末端执行器位姿有关；T为绳拉力矢量.对于尚未吹风状态的飞行器来说，WR＝［0，0，mg，0，0，0］，m为飞行器模型和内置天平等附件的质量；吹风后，作用在飞行器模型上的力螺旋矢量WR＝Wg＋Fa，Wg为重力作用在飞行器模型上的力螺旋矢量，Fa为风载荷作用在模型上的力螺旋矢量.

由于飞行器模型最终位姿是重力、绳拉力和风压等外力综合作用的结果，而飞行器重力及所受风压等都是既定的，要使飞行器模型稳定于期望位姿可通过改变绳索拉力来达到.根据式（1）所得的飞行器模型位于零位姿处仅受重力作用下的一组绳拉力T0，在较高速层流风场中并不能使飞行器位姿达到定位要求.然而，根据此组绳拉力作用下系统流固耦合分析的结果，可提取出系统结构矩阵JT′及绳索内力T′，利用式（1）可求解出该风场作用在模型上的力螺旋矢量Fa；再将Fa和零位姿结构矩阵JT0带入方程，可得到在该风载荷作用下模型要平衡于零位姿处的一组绳拉力T″，相较于仅在重力作用下计算的绳拉力T0更为准确.但由于新的绳拉力T″作用于飞行器上时，吹风后将达到一个新的平衡位姿，以至于风载荷和绳拉力作用在模型上的力螺旋矢量会发生变化，实际上将T″施加于WDPSS－8系统并不能使模型平衡于期望值.因此，需要不断迭代取得一组最合适的绳拉力值T，使飞行器模型位姿与既定位姿差值在定位精度范围内.提出的位姿补偿方法，如图4所示.

图4 WDPSS－8系统中飞行器模型位姿补偿方法Fig.4 Pose compensation method of the aircraft model in WDPSS－8system

利用迭代法对平均风速分别为60，100m·s－1的层流风场中的WPDSS－8系统末端位姿进行补偿，结果如表2所示.由表2可知：在平均风速为60m·s－1层流风场中，吹风后飞行器位姿X＝［－0.158，－0.262，－0.169，2.1，0，0.4］，Fa＝［－0.499 1，1.227 3，－16.079 1，－0.006 4，0.020 0，－0.052 6］，一次迭代后的位姿变化为X＝［－0.028，－0.269，－0.049，1.3，0.4，0.8］，Fa＝［0.062 8，1.240 4，－16.027 2，－0.004 4，0.022 8，－0.055 5］；而在平均风速为100m·s－1层流风场中，吹风后飞行器位姿X＝［0.181，－0.655，－0.398，6.6，0.2，1.8］，Fa＝［－3.352 8，2.941 1，－40.452 7，－0.078 1，－0.087 0，0.235 3］，一次迭代后的位姿变化为X＝［0.169，－0.664，－0.111，4.6，0.2，1.1］，Fa＝［－3.119 2，2.981 8，－40.488 2，－0.077 5，－0.086 8，0.231 4］，二次迭代后位姿变化为X＝［0.111，－0.777，－0.091，1.2，0，0］，Fa＝［－3.145 1，2.981 0，－40.496 8，－0.058 0，－0.083 7，0.303 1］.

此外，由表2可知：平均风速为60m·s－1层流风场中的飞行器位姿经一次迭代后可达定位精度要求，而平均风速为100m·s－1层流风场中的飞行器位姿需要经两次迭代后方可达到定位精度要求.因此，用上述迭代法调整绳索拉力值对系统末端位姿进行补偿是可行的.可得出以下结论：1）风速越大，风场对飞行器产生的一个－Z方向的作用力越大；2）当飞行器在风场中的位姿不同时，风载荷作用在飞行器上的力螺旋矢量不同，这是由于流固耦合效应作用的结果.因此，在位姿偏离较大的情况下，不能只通过一次迭代就使位姿达到定位精度.

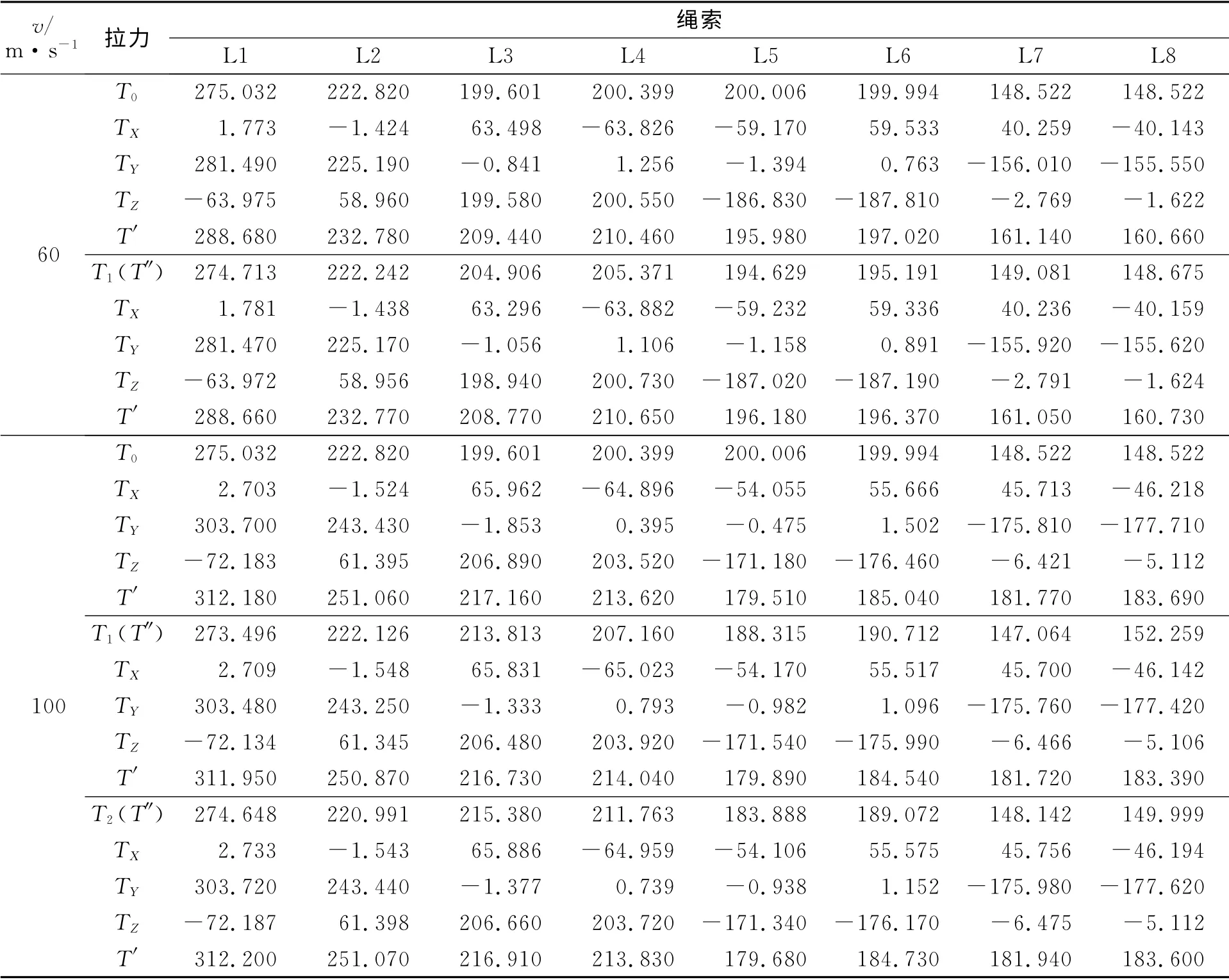
表2 采用迭代法对层流风场中的末端位姿进行补偿Tab.2 End－pose compensation of the laminar flow field using the iterative method N

4 结束语

基于ANSYS／CFX 对不同风速层流风场中WDPSS－8系统索系进行流固耦合分析，讨论了由于吹风后索的最终变形及绳索绳内力变化而导致的末端位姿偏离.分析得出在较高速的风场中，由于绳索与风场的耦合作用引起绳拉力作用在飞行器模型上的力螺旋矢量发生变化，最终将导致飞行器偏离既定位姿，超过风洞试验支撑系统定位要求.根据绳索变形情况、绳拉力和风载荷作用在模型上的力螺旋矢量，提出对WDPSS－8系统末端位姿进行补偿的方法，从而实现对飞行器模型的精确定位.

［1］LAFOURCADE P，LLIBRE M，REBOULET C.Design of a parallel wire－driven manipulator for wind tunnels［C］∥Proceedings of the Workshop on Fundamental Issues and Future Directions for Parallel Mechanisms and Manipulators.Quebec：［s.n.］：187－194.

［2］FARCY D，LLIBRE M，CARTON P，et al.SACSO：Wire－driven parallel set－up for dynamic tests in wind tunnel－review of principles and advantages for identification of aerodynamic models for flight mechanics［C］∥Proceedings of 8th ONERA－DLR Aerospace Symposium.Beijing：China Machine Press，2004：1878－1882.

［3］郑亚青，刘雄伟.绳牵引并联机构的研究概况与发展趋势［J］.中国机械工程，2003，14（9）：808－810.

［4］BERGAMANN A.Modern wind tunnel techniques for unsteady testing－development of dynamic test rig［EB／OL］.［2014－10－18］.http：／／link.springer.com／contenr／pdf／10.1007%2F978－3－540－95998－4＿5.pdf.

［5］XIAO Yang－wen，LIN Qi，ZHENG Ya－qing，et al.Model aerodynamic tests with a wire－driven parallel suspension system in low－speed wind tunnel［J］.Chinese Journal of Aeronautics，2010，23（4）：393－400.

［6］ZHENG Ya－qing，ZHAO Shuai－he.Research survey of technique about wire－driven parallel suspension systems used in forced oscillation experiments in low－speed wind tunnels for obtaining dynamic derivatives［C］∥Proceedings of 2011 3rd International Asia Conference on Informatics in Control，Automation and Robotics.Berlin：Springer，2011：131－138.

［7］JIAO Shao－ni，ZHENG Ya－qing，LIN Qi.The fluid－solid interaction analysis of WDPSS－8based on ANSYS［C］∥Proceedings of 2011 3rd International Asia Conference on Informatics in Control，Automation and Robotics.Berlin：Springer，2011：795－802.

［8］焦少妮.用于静态实验的低速风洞绳牵引支撑系统WDPSS－8索系流固耦合研究［D］.厦门：华侨大学，2012：1－93.

［9］郑亚青，焦少妮，杨永柏.低速风洞层流风场中WDPSS－8机器人系统索系流固耦合效应的动静力特性分析［J］.中国机械工程，2013，24（13）：1765－1772.

［10］王宏，郭彦林，任革学.索振动控制及其工程应用［J］.工业建筑，2003，33（7）：54－56.