稳定单叶调和凸函数和星像函数的构造

朱孟坤，黄心中

（华侨大学 数学科学学院，福建 泉州362021）

1 预备知识

单位圆盘D＝｛z‖z|＜1｝上的复值调和映照可表示为f（z）＝h（z）＋g（z），其中，h（z），g（z）为在D上的解析函数.Lewy［1］证明了单连通区域Ω上的调和映照f（z）＝h（z）＋g（z）是局部单叶的，当且仅当它的Jf（z）＝|h′（z）|2－|g′（z）|2≠0，当Jf（z）＞0时，称f（z）是保向的；否则，称f（z）为反向的.如果Ω上的单叶调和映照f（z）满足|g′（z）／h′（z）|≤t＜1，t为常数，则f（z）为Ω上的调和拟共形映照.关于拟共形映照的性质，可见文献［2］.如果为D上的单叶调和映照，Clunie等［3］提出了系数猜想，极值映照可由达到.该猜想在单叶调和映照的一些子集上成立，但在整个集合上成立与否仍未得到证明.近年来，许多学者对该猜想做了大量的研究［4－7］.文献［8－9］研究了单叶调和映照成为调和拟共形映照的性质.Hernández等［10］研究了单叶调和映照的稳定性问题，围绕调和映照及解析函数的稳定单叶性及稳定几何性质进行深入研究，对以上猜想的解决做了大量工作.

定义在D上的保向单叶调和凸映照对任意λ∈∂D，若都是D上的单叶凸映照，则称f（z）为D上的稳定调和凸映照（SHC）；如果都是D上的单叶星像映照，则称f（z）为D上的稳定调和星像映照（SHS＊）.Hernández等［10］研究D上k－凸解析函数的水平剪切函数为稳定调和凸映照的问题，证明了如下定理.

定理A对任意的λ且|λ|＝1，保向调和映照fλ（z）＝h（z）＋λg（z）为D上的调和凸映照的充分必要条件，是Fλ（z）＝h（z）＋λg（z）为D上凸解析函数.

定理B若是D上的保向单叶稳定调和凸映照，则对任意的λ∈，有h（z）＋λg（z）都是D上的凸函数.特别地，当λ＝0时，h（z）是D上的单叶凸函数.

定义1D上局部单叶解析函数称为k－凸解析函数，若φ（z）满足

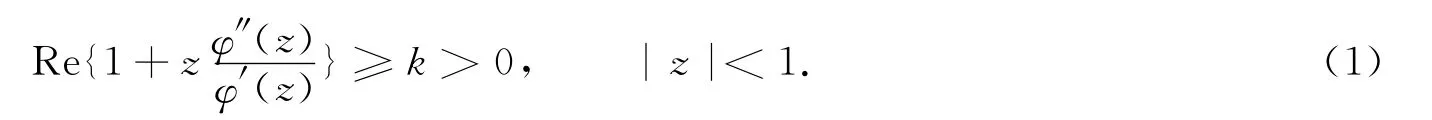
特别地，当式（1）中的非负常数k不存在时，称φ（z）为0－凸函数.

基于定理A，B，Hernández等［10］还证明了定理C.

定理C设φ（z）为一个k－凸解析函数，则存在μ∈D，当|μ|充分小时，由方程组

构造出来的调和映照f（z）＝h（z）＋g（z）∈SHC.

定理D定义在单位圆上的解析函数h（z），g（z），H（z）以及G（z）满足如下关系，即

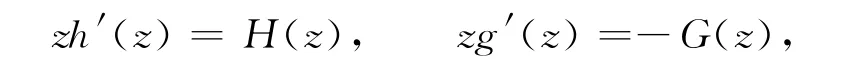
则f（z）＝h（z）＋g（z）∈SHC的充分必要条件是F（z）＝H（z）＋G（z）∈SHS＊.

2 主要结果及证明

由k－凸解析函数的定义可知：0≤k≤1.当k＝1时，恒等映照φ（z）＝z为D上的1－凸解析函数.构造一类k－凸解析函数，使得0≤k≤1.记函数其中，α为任意正实数.易证φ（z）在D上单叶解析.由调和映照的最小模原理可得

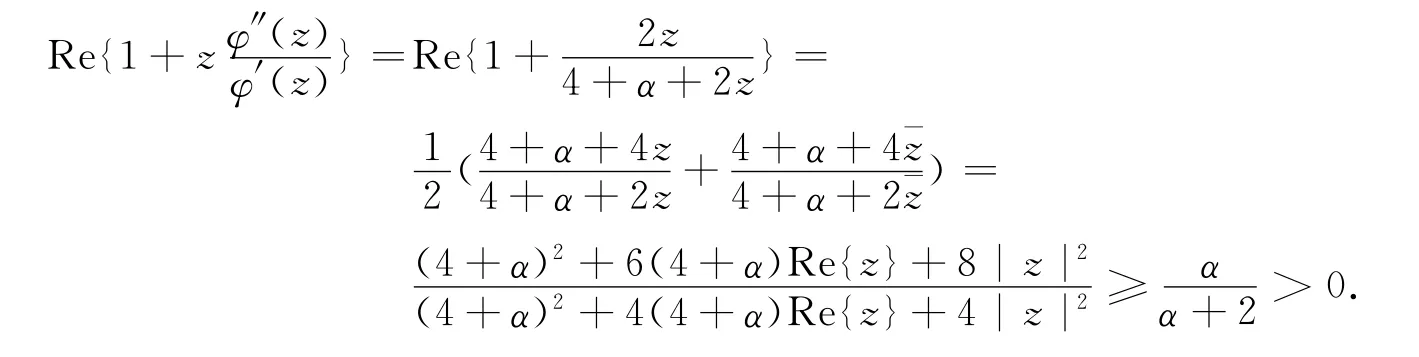
故φ（z）为－凸解析函数，当z→－1时，k→.当α＝0时，φ（z）为0－凸解析函数；当α→∞时，φ（z）为1－凸解析函数.

定理1存在一个φ0（z）为D上的单叶解析凸函数，由方程组

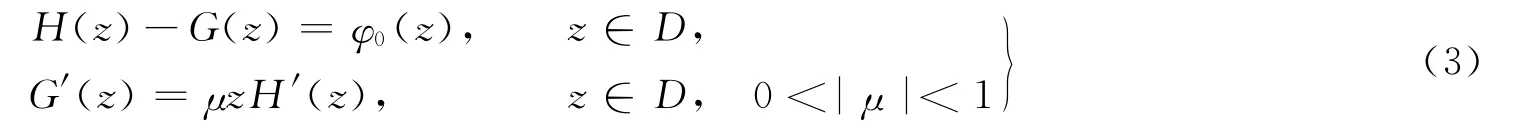
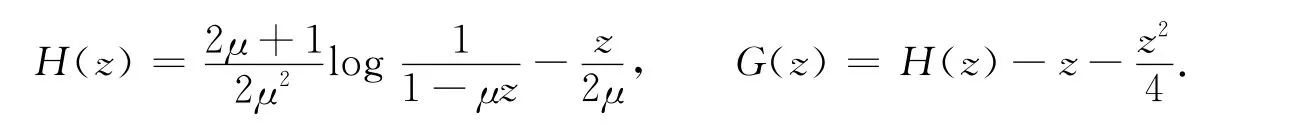
记（z）＝H（z）＋λG（z），λ∈∂D，易知（z）在D上单叶解析.又因为|λ|＝1，0＜|μ|＜1且z∈D，可知.根据调和映照最小模原理可得

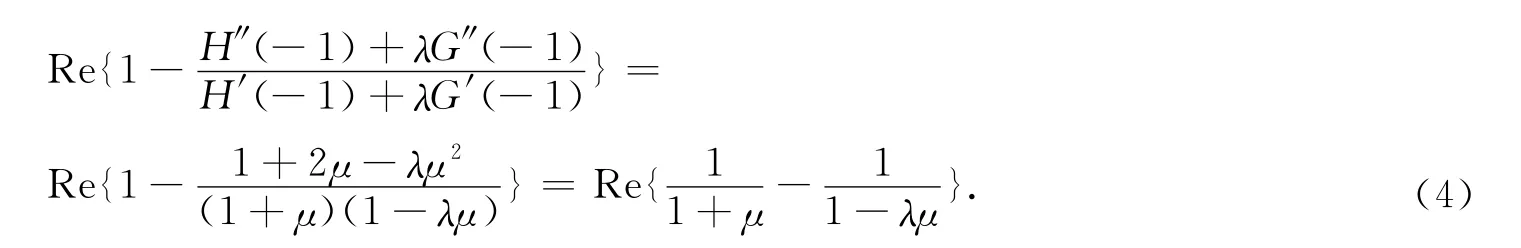
记μ＝ρexp（iθ），|ρ|＜1，令λ＝exp（－iθ），则式（4）恒小于等于零.故当0＜|μ|＜1时，（z）为非凸单叶解析函数，根据定理证毕.

由定理1可知：对于定理C，只有当φ（z）为k－凸函数时，由式（3）构造的调和映照f（z）＝h（z）＋才有可能是稳定凸的.为此，将μ的取值范围精确化，方便构造出更多的SHC类函数.

定理2设φ（z）是D上的k－凸解析函数（k＞0），则对于μ∈D且满足由方程组

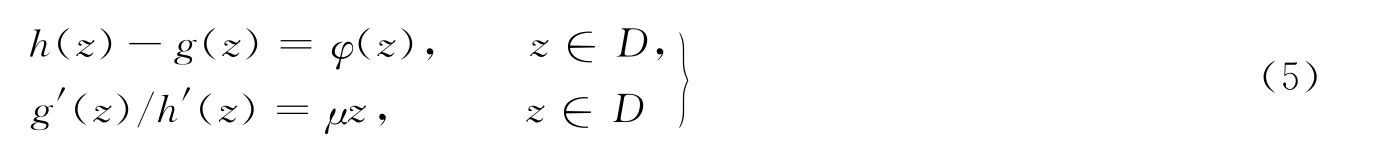
构造出来的单叶保向调和映照f（z）＝h（z）＋g（z）∈SHC.

证明 定义φθ（z）＝h（z）－exp（2iθ）g（z），ω（z）＝μz.根据定理A，只需验证函数φθ（z）在D内对于任意的θ∈（0，π）为凸解析函数.利用φ（z）为k－凸解析函数这个假设以及凸解析函数的特点，可得到

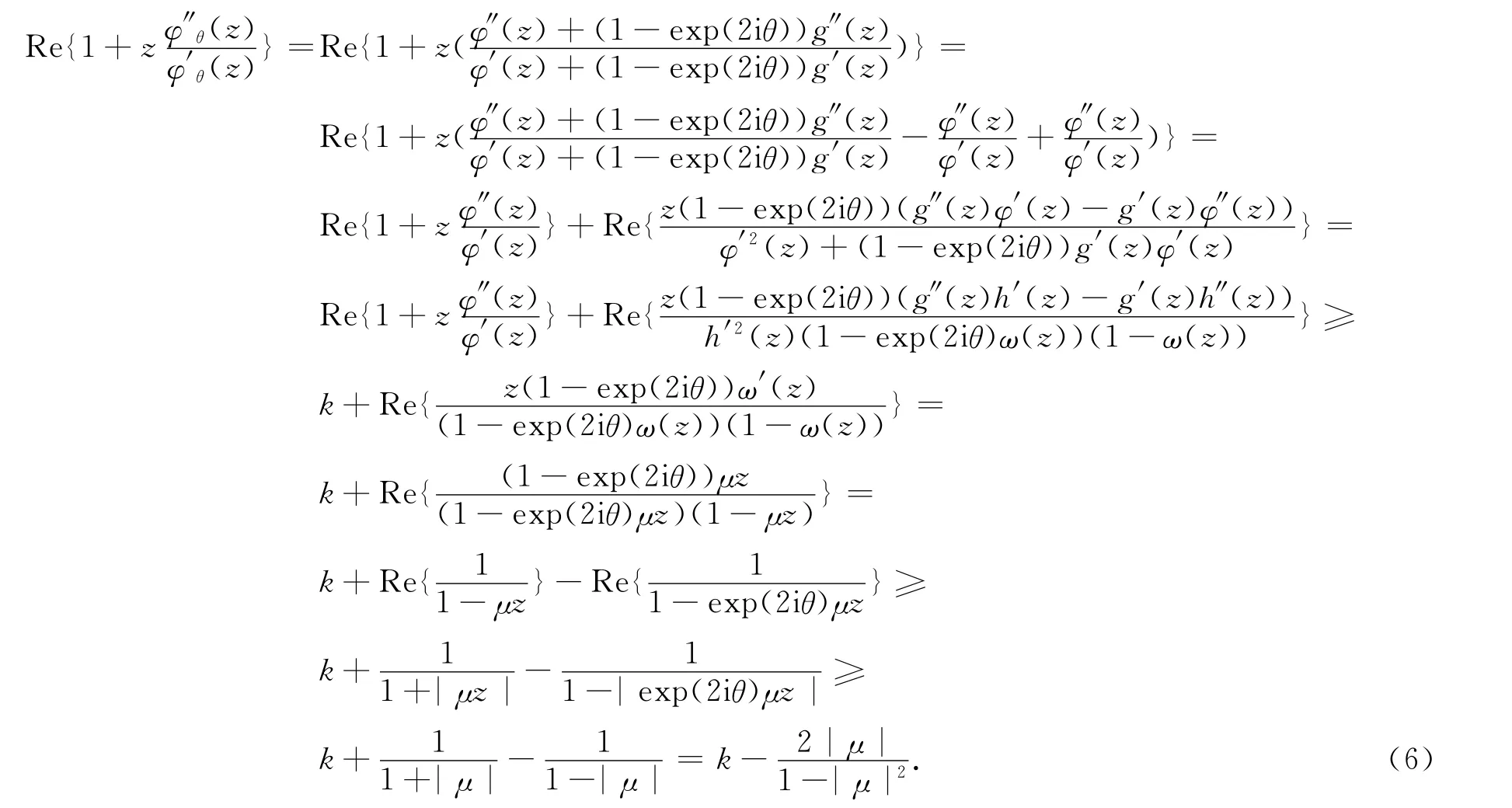
例1令φ（z）＝z，则φ（z）为1－凸函数，由定理2可知：仅当|μ|≤－1时，满足式（5）的解f（z）.分别取可得通过Mathematica软件，它们将D分别映成的区域，如图1所示.图1中：Re表示实部；Im 表示虚部.

通过探究定理2发现，ω（z）＝μz的形式并不是固定的，对此还可作如下推广.

推论1设φ（z）为D上的k－凸解析函数（k＞0）.则对于μ∈D且满足由方程组

构造出来的单叶保向调和映照f（z）＝h（z）＋g（z）∈SHC.

图1 单位圆盘D 经过fμ（z）映照后的图像Fig.1 Function fμ（z）maps Donto the domains respectively

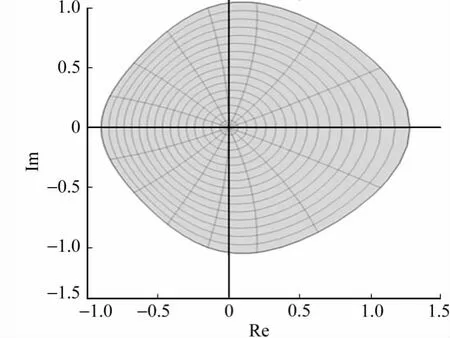
图2 单位圆盘D 经f（z）映照后的图像Fig.2 Function f（z）maps D onto the domain

例2令则且取μ＝得到方程组

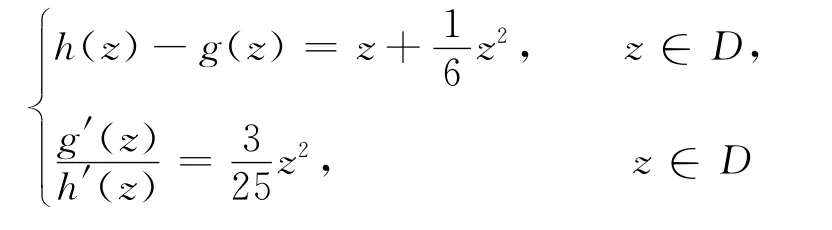
定理3设φ（z）是定义在D上的k－凸解析函数.则对于μ∈D且满足使调和映照f（z）＝h（z）＋g（z）为D上关于原点的稳定调和星像映照，其中，h（z），g（z）分别满足

证明 记

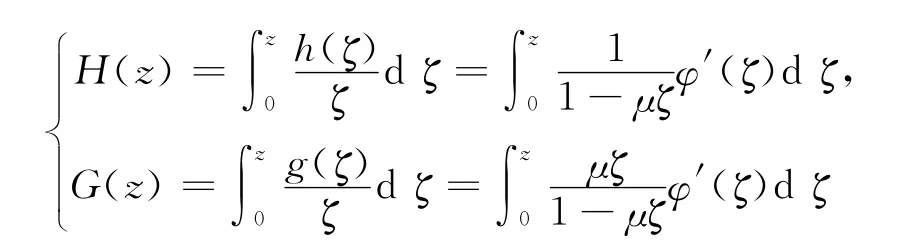
由简单计算可得，H（z）－G（z）＝φ（z），G′（z）／H′（z）＝μz.由定理2可知F（z）＝H（z）＋G（z）为D上的稳定调和凸映照，又因为zH′（z）＝h（z），zG′（z）＝－g（z）且h（0）＝g（0）＝0，由定理D 可知为D上的关于原点的稳定调和星像映照.

例3对于D上的1－凸解析函数φ（z）＝z.取.根据定理3可得，故

通过Mathematica软件，f（z）将D映成的区域，如图3所示.类比推论1，很容易得到如下推论.

图3 单位圆盘D 经f（z）映照后的图像Fig.3 Function f（z）maps D onto the domain

推论2设φ（z）为D上的k－凸解析函数，则对于μ∈D且满足使调和映照f（z）＝h（z）＋g（z）为D上关于原点的稳定调和星像映照.其中，h（z），g（z）分别满足

推论2可根据推论1、定理3及定理D 直接得出.

［1］LEWY H.On the non－vanishing of the Jacobian in certain one－to－one mappings［J］.Uspekhi Mat Nauk，1948，3（2）：216－219.

［2］AHLFORS L V.Lectures on quasiconformal mappings［M］.New Jersey：Van Nostrand Princeton，1966：15－22.

［3］CLUNIE J.SHEIL－SMALL T.Harmonic univalent functions［J］.Ann Acad Sci Fenn Ser（A），1984，9（1）：3－25.

［4］石擎天，黄心中.调和映照与其剪切函数的单叶性［J］.华侨大学学报：自然科学版，2013，34（3）：334－338.

［5］王其文，黄心中.在微分算子作用下调和函数的单叶半径估计［J］.华侨大学学报：自然科学版，2014，35（2）：227－231.

［6］潘旭玲，黄心中.一类单位圆盘上单叶调和映照的延拓定理［J］.华侨大学学报：自然科学版，2013，34（6）：701－705.

［7］BSHOUTY D，LYZZAIK A.Problems and conjectures in planar harmonic mappings［J］.J Analysis，2010，18：69－81.

［8］黄心中.单位圆到水平条形无界区域的调和拟共形映照［J］.数学学报：中文版，2014，57（7）：875－880.

［9］HUANG Xin－zhong.Harmonic quasiconformal mappings on the upper half－plane［J］.Complex Variables and Elliptic Equations，2013，58（7）：1005－1011.

［10］HERNÁNDEZ R，MARTÍN M J.Stable geometric properties of analytic and harmonic functions［J］.Math Proc Camb Phil Soc，2013，155（2）：343－359.

［11］DUREN P.Univalent functions［M］.New York：Springer－Verlag，1983：40－45.

［12］DUREN P.Harmonic mappings in the plane［M］.Cambridge：Cambridge University Press，2004：29－56.