基于梯度强度立柱的客车侧翻安全性多目标优化设计
周莎,张勇,张成,李奇
(华侨大学 机电及自动化学院,福建 厦门361021)
客车侧翻事故是特大交通事故的主体.客车因其所载乘客较多,经常出现群死群伤的现象,造成恶劣的社会影响.因此,对客车侧翻安全性进行研究具有重要意义[1].为了更好地研究客车侧翻事故,国内外都相继出台了客车侧翻实验的法规,较典型的是欧洲的ECE R66法规,GB 17578-2013《客车上部结构强度要求及试验方法》详细地规范了客车上部结构强度要求和相关的试验方法[2-3].对于客车侧翻安全性的研究,Su等[4]基于代理模型,利用响应面来实现客车多目标优化;Liang等[5]通过优化每根立柱厚度来改善客车上部结构强度和吸能性;高云凯等[6]基于客车上部结构关键零部件截面形状进行侧翻安全性多目标优化.然而,这些研究并未考虑到侧翻过程中侧围立柱不同位置受力不均匀的特点.本文针对这一现象提出一种新型的梯度强度立柱结构,使立柱不同位置的强度与受力匹配,从而减小侧围的挤压变形,提高侧翻安全性.
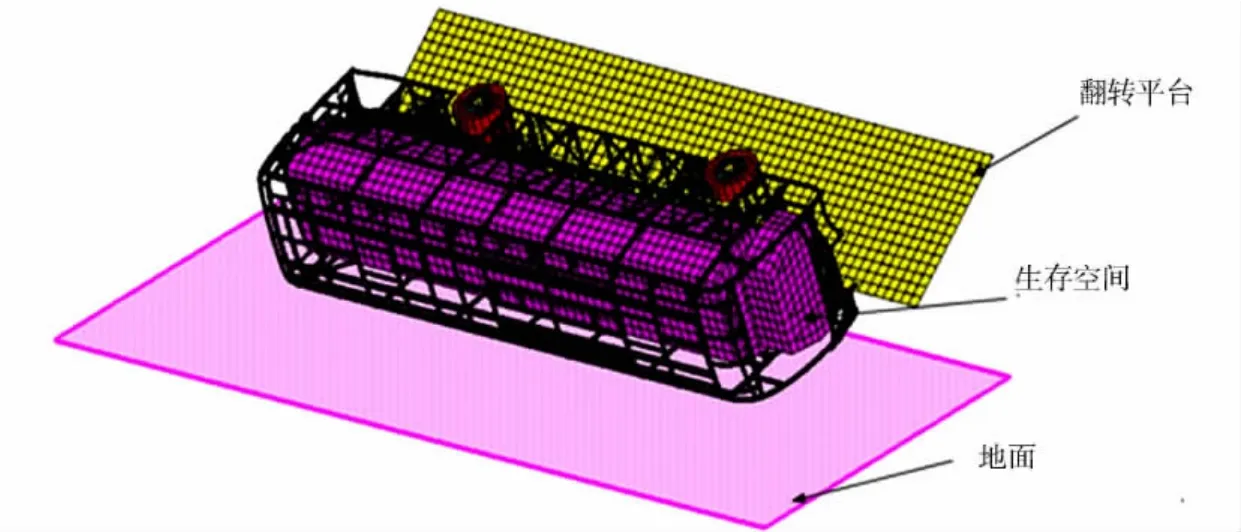
图1 客车侧翻有限元模型Fig.1 Bus rollover finite element model
1 客车有限元模型的建立
以某型号全承载大客车为研究对象,并建立该客车的有限元模型,如图1 所示.模型主要包括车身骨架、底架和车轮等.其他部件如发动机、油箱、蒙皮和座椅等均以集中载荷或均布载荷等效配重的方式加载到对应几何位置的节点上,保证整车有限元模型的质心高度位置和实车的基本吻合,误差控制在2%以内[7].基于ECE R66法规建立的客车有限元侧翻模型,其主要包括车身部分、翻转平台和地面.并且,为方便评价客车上部结构的强度及安全性,模型依据ECE R66定义了乘员的生存空间.
为了保证乘员安全性,客车侧翻过程中车身部件不能侵入生存空间.整车有限元模型共有412 967个单元,419 535个节点.车身骨架的材料为Q345,密度为7 800kg·m-3;弹性模量为210GPa;泊松比为0.3;屈服极限为345 MPa.
2 客车侧翻安全性分析及验证
建好的客车侧翻有限元模型采用LS-DYNA 进行数值仿真分析,整个分析过程从客车撞地瞬间到车身完全离开地面为止,历时250ms.侧翻碰撞过程中车身与地面的撞击力,如图2所示.由图2可知:整个过程有两个波峰值,从开始到0.008s时车身结构与地面发生撞击,此时撞击力达到最大值1 570 kN;到0.078ms左右时碰撞力达到另一个峰值551kN,此时车身变形量达到最大;到0.215s后,碰撞力几乎为零,说明此时车身开始弹离开地面.
碰撞过程中的能量曲线,如图3所示.由图3可知:整个过程能量守恒,沙漏能所占比例小于5%.为验证该有限元模型的有效性,结合与该车型结构相近的对标车型的侧翻实验,进行对比分析,结果如表1所示.表1中:侧翻过程中侧围每根立柱与生存空间的最小距离(入侵量)分别为D1,D2,D3,D4,D5,D6,D7.由表1可知:对标模型的侧翻初始侵入与当前模型较为吻合,因此,可认为整车模型和分析都是合理、可靠的[8].
侧翻碰撞过程中在立柱上间隔均匀选取5个测试点,侧围立柱的应力云图,如图4所示.由图4可知:侧翻过程中其立柱不同位置的应力水平差别较大.
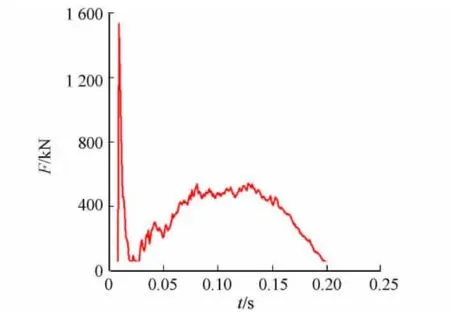
图2 撞击力曲线 Fig.2 Impact force curve
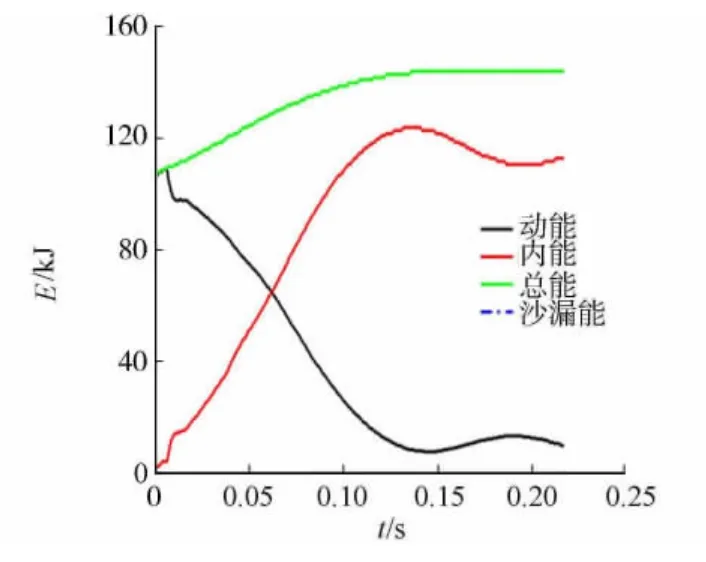
图3 车身能量曲线Fig.3 Body energy curve

表1 对标模型与当前模型侧翻入侵对比Tab.1 Rollover invasion comparison of simulation and experiment model
侧翻过程中车身结构最大变形,如图5所示.由图5可知:碰撞过程中,生存空间明显被入侵,不满足ECE R66法规要求,因此,需要强化车身上部结构强度来提高客车侧翻安全性能.
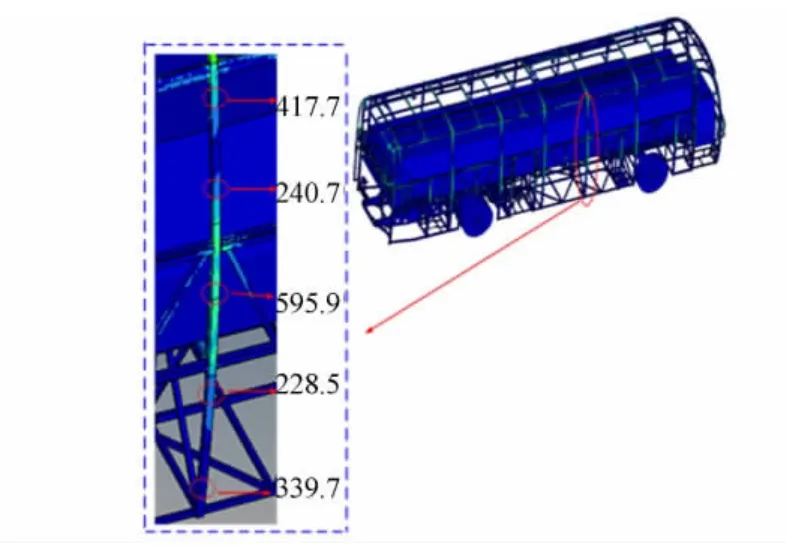
图4 侧围立柱的应力云图Fig.4 Stress nephogram of side wall pillar(MPa)
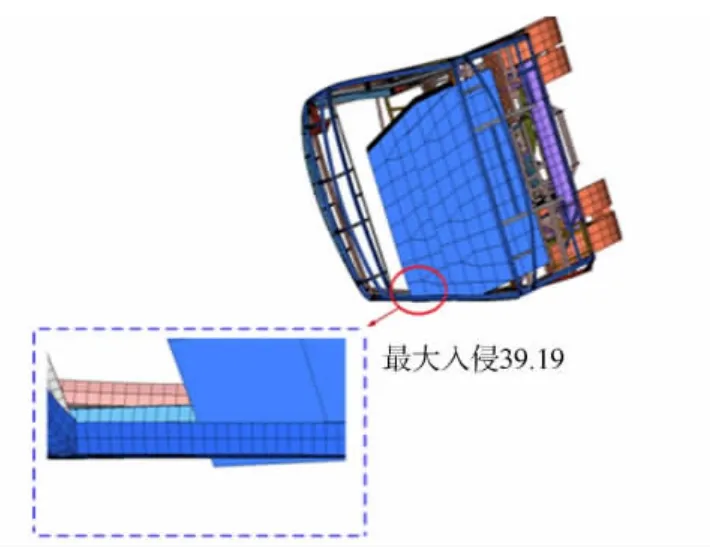
图5 侧翻入侵示意图Fig.5 Schematic view of rollover invasion(mm)
3 梯度强度立柱结构侧翻安全性的优化
3.1 设计流程的优化
从客车侧翻过程可以看出:侧围立柱是关键的承力部件,侧翻碰撞过程中客车立柱不同位置受力相当不均匀.因此,提出了一种新型的梯度强度立柱结构,使立柱不同位置的强度与受力匹配,从而减小侧围的挤压变形,提高侧翻安全性.为了进一步使立柱结构强度分布更加合理,基于客车梯度强度立柱的强度匹配进行客车侧翻安全性的多目标优化流程,如图6所示.
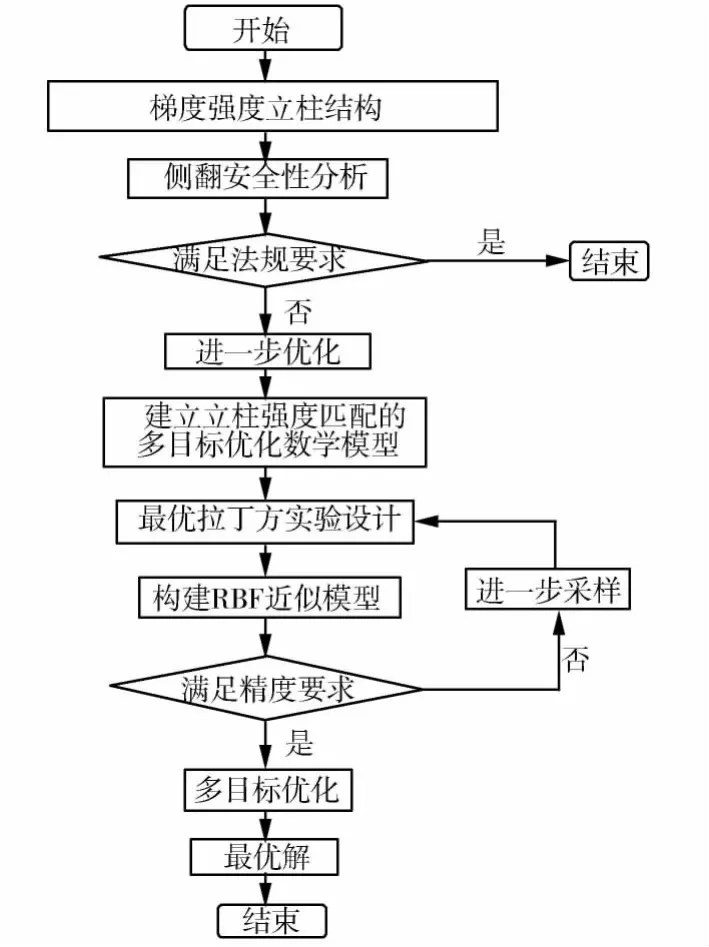
图6 客车车身多目标优化设计流程图Fig.6 Design flow chart of bus body multi-objectiveoptimization design flow
3.2 梯度强度立柱结构及侧翻分析
客车梯度强度立柱结构是把立柱均匀分为6单元,每个单元强度不一样,且呈梯度变化,客车侧围梯度强度立柱结构示意图,如图7所示.
采用热成型方法[9-10]加工的梯度强度立柱结构,如图8所示.该结构将客车每根立柱均匀分为6 个单元:Q1,Q2,Q3,Q4,Q5,Q6,6个单元的强度沿高度变化.根据热成型的梯度强度立柱结构具有5种屈服强度,6个单元对应的屈服强度为400,500,650,800,1 000,1 000 MPa.
为了验证梯度强度结构的性能,将初始客车立柱替换为梯度强度立柱,对其进行数值仿真分析,得到的各立柱对生存空间的入侵量,如表2所示.表2中:负数表示有入侵情况.由表2可知:相对于原始模型的侧翻,采用梯度强度立柱结构后的安全性有了明显提高,但立柱对生存空间还有一定的侵入量,因此,仍需要对其进行的优化设计.

图7 客车侧围立柱结构示意图Fig.7 Bus side wall pillars structure

图8 梯度强度立柱结构Fig.8 Gradient strength pillar structure

表2 立柱对生存空间入侵量Tab.2 Pillar on the amount of living space invasion
3.3 客车侧翻多目标优化数学模型
虽然单目标优化能够改善设计性能,但单目标优化在复杂的设计要求下不能为设计师提供多种可选的设计方案[11].在汽车优化设计中应该综合考虑汽车各方面因素,实现汽车更多性能要求.多目标优化不同于单目标优化,最后所得的最优解不是唯一解,而是一个Pareto最优解集或Pareto前沿.求解多目标问题实质就是寻求Pareto最优解集的过程[12].
客车侧翻过程中,乘客受伤害有两种主要形式[13]:被入侵的生存空间对乘客进行的挤压,乘客与车体之间的二次碰撞.因此,为降低客车侧翻时对乘客的伤害,以客车梯度强度立柱结构为优化对象,选取立柱6个单元的屈服强度和每根立柱厚度做为设计变量,以生存空间的侵入量为设计约束,以侧翻碰撞后车身吸收能量和立柱质量为设计目标,建立基于梯度强度立柱结构强度匹配的客车车身多目标优化数学模型,即

式(1)中:E为侧翻中车身吸收的能量;M为立柱结构质量;Q1,…,Q6为立柱结构6个单元的屈服强度;t1,t2,…,t7为对应的每根立柱厚度;立柱厚度下限tj,l为1.5mm,上限tj,h为3.5mm;Di为入侵量.
3.4 近似模型的建立
在工程优化问题中,对于一些高度非线性问题,如汽车碰撞分析等,直接利用有限元模型进行优化迭代过程非常耗时.因此,近似模型技术得到了广泛的关注和应用.由于径向基近似模型(radial basis function,RBF)针对客车侧翻碰撞这类高度非线性问题有较好的预测精度和稳健性,因此,基于RBF径向基方法构建了各个响应的近似模型.近似模型的建立包括实验设计采样和近似模型技术两方面[14].
3.4.1 最优拉丁方实验设计 最优拉丁方采样方法能使采样点比较均匀地分布在采样空间,是一种“充满空间”采样技术,用较少的试验点就能真实地反映采样空间信息的特点[15].因此,对客车梯度强度立柱结构6个单元的屈服强度(Q1,…,Q6)和每根立柱厚度(t1,t2,…,t7)进行了60次最优拉丁方采样.
3.4.2 RBF近似模型 RBF是以径向函数为基函数,通过线性叠加的方式构造出来的模型.一般情况下任何函数都可以表示为一组基函数的加权和,可以实现从样本输入到基函数输出之间的一种非线性映射关系[16],其基本数学表达式为
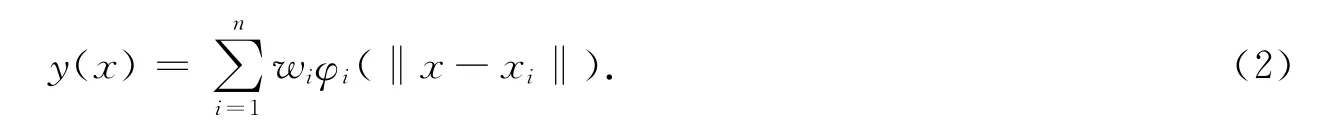
式(2)中:x为设计变量;n为样本点个数;wi为线性叠加权系数;‖x-xi‖为对应预测点和第i个样本点之间的欧氏距离;径向函数为φi(‖x-xi‖).
3.4.3 近似模型的精度检查 近似模型的精度决定了最优结果的可行性,因此,必须开展近似模型精度的验证.采用工程中常用的复相关系数R2检测,R2定义[17]为

式(3)中:n为样本数;为第i个样本点的近似模型预测值;yi为第i个样本点的真实值(有限元计算值);为样本均值.
R2的值在0到1之间,R2越接近1,则表明近似模型的精度越高.通过验算,基于最优拉丁方样本点与RBF近似技术得到的各近似模型的R2值,如表3所示.
由表3可知:所有近似模型的R2值都较接近1,说明近似模型的精度都比较高,可用它来代替有限元模型进行多目标优化.

表3 设计响应的近似模型精度Tab.3 Approximate model accuray cof design responses
部分响应的高精度RBF近似模型,如图9所示.
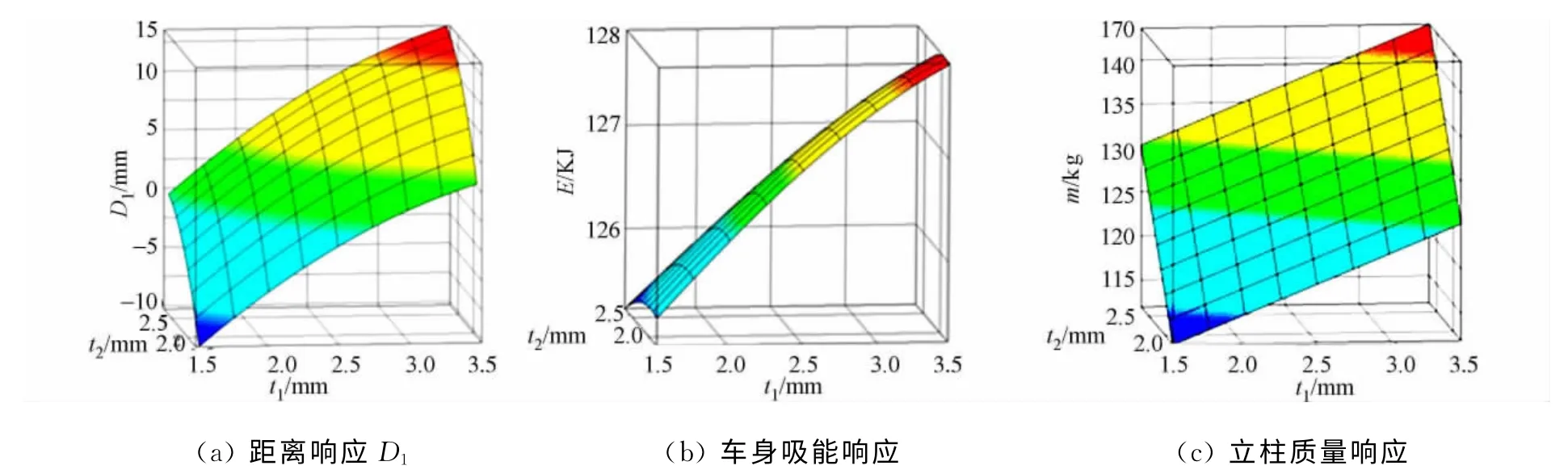
图9 部分响应近似模型Fig.9 Approximate model of partial response
4 优化结果与讨论
采用NSGA-Ⅱ对各个响应的近似模型进行多目标寻优,质量与能量吸收之间的Pareto前沿曲线,如图10所示.Pareto前沿是一个优化解集,相对单目标优化而言,它能为工程设计人员提供更多的设计方案,常根据设计的实际需求和经济性来选取最优设计方案.图10中:红色标记为在Pareto前沿曲线间隔均匀选取的3组解.
3组最优设计变量所对应响应值,如表4所示.由表4可知:3组皆满足ECE R66法规的要求;解1 侧重于车身减重;解2兼顾车身减重和能量吸收;解3侧重于能量吸收.综合兼顾吸能和轻量化的目的,最后决定以解2为最终解.
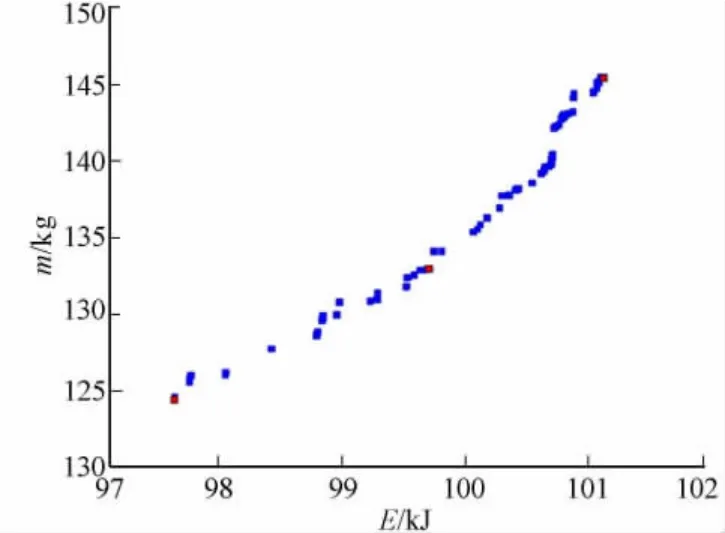
图10 设计目标的Pareto前沿Fig.10 Pareto front of design objectives

表4 3组Pareto最优解对应的响应值Tab.4 Three groups of Pareto optimal solutions corresponding response
由于优化后整车重量减轻,侧翻时初始能量减小及车身变形减小,车身吸能比优化前减少了,而乘客与车体发生二次碰撞而受伤害的可能性并没有增大.初始设计和优化后车身与地面碰撞时的撞击力曲线,如图11所示.由图11可知:优化后碰撞力峰值比初始模型降低16.9%,从而大大降低二次碰撞时对乘员的伤害.
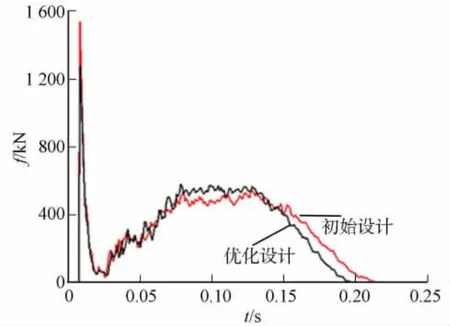
图11 优化前后碰撞力曲线对比Fig.11 Comparison of the collision force before and after optimization
5 结论
根据客车侧翻过程中立柱不同位置受力不同的特点,提出了一种新型梯度强度立柱结构,把每根立柱强度沿高度方向均匀分为6个单元,使得立柱不同位置强度与受力匹配.
结合最优拉丁方实验设计采样与RBF 近似技术,对立柱结构的强度与厚度进行了多目标最优匹配.优化结果表明:1)梯度强度立柱结构能明显提高客车侧翻安全性能;2)针对客车侧翻优化问题,采用RBF径向基近似模型有较高的精度,并大幅提高了优化效率;3)梯度强度立柱结构实现立柱结构减质量10.4%,达到了轻量化的目的;4)结合RBF 模型和NSGA-Ⅱ算法应用于客车侧翻的多目标优化中,得出了Pareto最优解集,可以为设计人员提供多套设计方案参考.
[1]苏銮,李高波,吕光辉.长途客车交通事故原因及实例分析[J].交通企业管理,2013(8):71-72.
[2]中国公路车辆有限公司,金龙联合汽车工业有限公司.GB 7578-2013客车上部结构强度要求及试验方法[S].北京:中国标准出版社,2014:13-18
[3]杨瑞峰,樊江顺,崔海涛,等.基于ECE R66法规的某大客车上部结构强度[J].公路交通科技,2011,28(10):136-140.
[4]SU Rui-yi,GUI Lian-gjin,FAN Zi-jie.Multi-objective optimization for bus body with strength and roller safety constraints based on surrogate models[J].Structural and Multidisciplinary Optimization,2011,44(3):431-441.
[5]LIANG C C,LE G N.Optimization of bus rollover strength by consideration of the energy absorption ability[J].International Journal of Automotive Technology,2010,11(2):173-185.
[6]高云凯,张朋,吴锦妍,等.基于Kriging模型的大客车侧翻安全性多目标优化[J].同济大学学报:自然自然版,2012,40(12):1882-1887.
[7]胡泊,客车侧翻安全性仿真研究及试验验证[D].西安:长安大学,2012:55-58.
[8]马晓光,王秋林,那景新,等.客车侧翻结构安全性仿真分析及改进设计[J].客车技术与研究,2011,41(8):31-33.
[9]高云凯,高大威,余海燕,等.汽车用高强度钢热成型技术[J].汽车技术,2010(8):56-60.
[10]林建平,王立影,田浩彬,等.超高强度钢板热冲压成形研究与发展[J].热加工工艺,2008,37(21):140-144.
[11]ZHANG Yong,SUN Guang-yong,LI Guang-yao.Optimization of foam-filled bitubal structures for crashworthiness criteria[J].Materials and Design,2012,38:99-109.
[12]关志华,寇纪淞,李敏强.一种改进的非支配排序遗传算法INSGA[J].天津大学学报:自然科学版,2002,35(4):429-434.
[13]范子杰,马林,桂良进,等.大客车侧翻安全性多目标优化[J].系统仿真学报,2012,24(5):1109-1113.
[14]李恩颖,近似模型优化体系关键技术研究及应用[D].长沙:湖南大学,2009:2-8.
[15]LIEFVENDAHL M,STOCKI R.A study on algorithms for optimization of latin hypercubes[J].Journal of Statistical Planning and Inference,2006,136(9):3231-3247.
[16]陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].长沙:湖南大学,2012:12-18
[17]廖兴涛,张维刚,李青,等.响应表面法在薄壁构件耐撞性优化设计中的应用[J].研究工程设计学报,2006,13(5):298-302.

